深度学习下模糊高光谱图像复原数学模型仿真

苏乐辉

(泉州信息工程学院,福建 泉州 362000)

1 引言

在高光谱图像拍摄过程中,由于拍摄设备运动,导致载荷平台的振动,从而采集到的高光谱图像较为模糊。图像的空间、光谱的分辨率决定图像质量。空间分辨率能够展现出图像空间数据的详细程度;光谱分辨率则表现出其对光谱细节的区分能力,提升图像分辨率是解决模糊图像最有效的方法,但在提升图像空间、光谱的分辨率却是当前面临最大难题[1-2]。现阶段,提升光谱分辨率只能通过降低空间分辨率方式,解决此问题,需要革新成像设备,周期长,且成本昂贵。因此,可通过图像复原技术,借助信号预处理方式提升高光谱图像的空间、光谱的分辨率,成为解决此问题的唯一有效方法[3]。

诸多学者对模糊高光谱图像复原算法进行深入研究。张华卫等人[4]通过Canny算子提取模糊高光谱图像的纹理特征,采用二次约束模型建立图像复原数学模型,进而将模糊图像复原;谭晏松等人[5]首先调整模糊图像饱和度,利用粒子群优化方法平衡图像色彩,完成模糊高光谱图像的复原;赵晋陵等人[6]采用主成分分析算法将高光谱数据降维处理,通过联合局部二值模式提取图像特征,利用最近邻分类器识别出图像上噪声并过滤掉,从而清晰的高光谱图像。二次约束、PSO复原方法能够有效保证复原图像质量,但复原运算较为复杂,用时较长;K-最近邻算法图像复原速度较快,但复原结果不理想。

为解决上述方法存在的问题,研究一种基于深度学习的模糊高光谱图像复原数学模型方法。深度学习能够利用卷积神经网络的逐级卷积操作方式,提取出高光谱图像的空间维特征、光谱维特征,有效保证复原图像质量。实验结果表明,所提方法能够实现对模糊图像的复原,且图像复原时间短。

2 模糊高光谱图像复原数学模型构建

2.1 高光谱成像过程分析

高光谱成像起点即为遥感数据源,其能量主要来源于太阳,太阳放出的电磁波在真空介质下,传播到地球表面的大气层附近,一部分电磁波被大气层表面反射到太空,剩余部分入射至大气层中,通过其内部气体的相互作用,传播到地物表面[7-8]。目标物体接收到的能量在反射作用下,物体携带光谱信息,由信号接收装置接收,经过处理后得到高光谱图像,详细过程如图1(a)所示。

图1 高光谱成像与链路模型

根据高光谱成像原理可知,其能量相互作用过程可看成1个系统,也就是成像链路,如图1(b)所示。此链路主要由信息源、大气、目标物体及其传感装置的模型组成[9],采用式(1)表述高光谱成像c,即:

c=∭l(x,y,λ)τ(x,y,λ)r(x,y,λ)b(x,y,λ)dxdydλ

(1)

式中,λ描述光谱维度;x与y即为空间维、光谱维的变量;l(x,y,λ)描述信息源模型;τ(x,y,λ)描述大气模型;r(x,y,λ)与b(x,y,λ)分别描述目标物体模型及其传感装置的模型。

2.2 图像退化模型

高光谱成像过程中,由于高光谱拍摄平台以振动方式进行姿态运动,这会使图像质量退化,从而采集到高光谱图像较为模糊[10]。针对此问题,通过分析拍摄平台每一个姿态的偏移与振动导致图像模糊成因,即像元运动偏移量,结合高光谱成像原理,分析出物体光谱与拍摄姿态二者间的联系及其退化数学模型。

高光谱图像数据可看成1个三维立方体,各波段都有各自的空间图像。假设用e(x,y,λ)描述振动后的光谱数据,即模糊图像的光谱数据,其表达式为。

e(x,y,λ)=f(x,y,λ)h(x,y,λ)c+s(x,y,λ)

(2)

式中,f(x,y,λ)代表实际高光谱图像信息;h(x,y,λ)描述图像点扩散函数;s(x,y,λ)代表高光谱图像噪声。

在理想状态下(无噪声),f(x,y,λ)通过一个平面运动,x1(t)描述x方向上移动量,y1(t)描述y方向上移动量,t描述运动所用时间,则模糊后的数据求解过程为:

(3)

根据式(3)可知,模糊高光谱信息立方体的λ是固定不变的,也就是h(x,y,λ)与λ无关,将式(3)中λ根据光谱分辨率Δλ离散处理,得出:

(4)

式中,n描述的波段数量;fi(x,y)描述第i个波段的空间图像。

假设Fi(u,v)、E(u,v,ω)为fi(x,y)、e(x,y,λ)的傅里叶变换结果,则

(5)

式中,ω描述姿态角度;u、v即为x方向和y方向频域变化量。将式(5)整理,可得:

(6)

式中,H(u,v)即h(x,y)的傅里叶变换的结果,则有:

(7)

通过式(2)-式(7)分析出模糊高光谱图像的退化原理,进而找到模糊图像与实际图像之间关系,为后面模糊图像复原数学模型提供理论基础。

2.3 模糊图像复原数学模型

2.3.1 基于3D卷积网络的高光谱图像复原技术

模糊高光谱图像复原通常利用深度学习下卷积神经网络完成模糊图像复原,其将图像中各帧都看成一个单独且静止的二维图像处理,通过卷积神经网络检测每一帧目标的动作。但此方法忽略连续帧之间的目标运动信息,影响模糊图像复原效果。由此,采用3D卷积方法完成模糊图像复原,该方法能够将图像之间的运动信息融合到图像分析中,并通过相邻帧之间产生的许多信息通信,在各通道进行卷积与下采样,进而得到沿图像空间维与光谱维的特征,再将所有特征重组,最终得到现实的高光谱图像,完成模糊图像复原,详细过程如图图2(a)所示[11]。

图2 深度学习下模糊高光谱图像复原

从图2(a)可知,3D卷积网络主要由1层3D浅层特征提取层、2层3D卷积层与2层激活函数、1层三维反卷积层、3D重建层构成。其中,3D浅层特征提取层负责采集高光谱图像的浅层特征;3D卷积层由2个三维数据立体组成,任意卷积层都需要借助激活函数得到特征增加非线性因子;3D反卷积层负责将LR空间变换至HR空间,得到HR空间的特征图谱,从而实现高光谱图像采样;3D图像重建层即输出层,用于重组特征图谱,生成HR图像,进而得到清晰的高光谱图像[12]。

2.3.2 复原实现

在二维卷积中,卷积核的深度和输入图像的通道数量相等,进行卷积操作过程中,卷积核只能沿两个方法进行滑动,即图像高、宽方向,滑动遍历结束后获得通道数是1的二维图像。而在三维卷积中,卷积核深度始终小于输入图像通道数量[13],如图2(b)所示。

从图2(b)看出,3D卷积核以三维立方体方式展现出来,进行卷积操作时,不仅能从图像宽、高滑动遍历,还可以从光谱维上滑动遍历,遍历到位置经过卷积运算可得到特定值[14]。由于3D卷积核在三维空间内滑动,获得的结果依旧是三维图像。

卷积详细过程为:选取大小为2×2×2的卷积核,在模糊高光谱图像像元矩阵上按照设定的步长滑动,将感受野范围内采用加权求解与卷积计算,借助非线性因子得到输出的特征映射[15]。

在深度学习下,设定3D卷积层共k层,任意一层都会产生k1个特征图,则卷积模糊高光谱图像复原数学模型为:

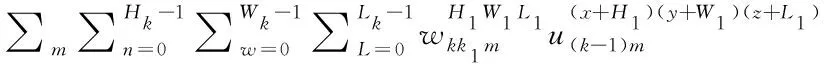
(8)

通过式(8)提取出高光谱空间维与光谱维特征,然后将其输入三维反卷积层放大处理,最后经3D重建层重建,得到清晰高光谱图像,进而实现了模糊高光谱图像复原。

3 仿真过程与结果分析

3.1 可视化效果分析

实验随机选取1张模糊高光谱图像,其空间尺寸为590×350,波段数量为240个,波长范围410nm-1200nm,采用二次约束、K-最近邻与PSO方法与所提方法复原处理,不同方法的图像复原效果分析如图3所示。

图3 不同方法的图像复原效果分析

从图3能够明显看出,所提方法模糊高光谱图像复原效果最佳,而二次约束、K-最近邻与PSO方法的模糊高光谱图像复原效果较差,存在不同程度的细节模糊。通过对比可知,所提方法的复原效果最佳,因其能根据高光谱成像原理及其退化原因得出模糊图像与实际图像之间相关性,通过深度学习提取图像各维度特征并重组,从而得到复原图像较为理想,对比方法只能提取图像部分特征,图像复原效果较差。

3.2 量化指标对比分析

3.2.1 空间维度分析

空间维度最常用评价指标为峰值信噪比(PSNR),其是指图像信号最大功率与噪声功率比值,设定H2×W2×L2表示模糊高光谱图像尺度;Q表示实际高光谱图像;Q1表示复原后的高光谱图像,其计算过程如式(9)所示。

(9)

式中,PSNR值越大,表示图像空间维度特征提取越多,图像失真越少。

根据式(9)分别求解不同方法下复原图像的峰值信噪比实验结果如图4所示。

图4 复原图像的峰值信噪比情况

图4中,所提方法每张高光谱图像复原的峰值信噪比在6dB以上,而二次约束、K-最近邻与PSO方法的复原信噪比则在0～6dB,通过对比可知,所提方法的峰值信噪都大于对比方法,表明所提方法的图像失真最少,复原效果最好,这是由于所提方法能够在高光谱图像空间维上进行特征提取,并能保证特征提取数量与质量,为此复原图像的峰值信噪比值较高。

3.2.2 光谱维度分析

光谱相关系数是衡量光谱维特征提取质量重要指标之一,其取值范围为[-1,1],值越大表明光谱相似性越大,此复原方法越好,计算过程为:

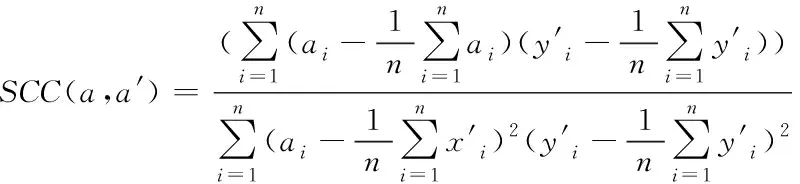
(10)

式中,a、a′代表图像2个不同的像元。根据式(10)得出四种方法下复原图像光谱相关系数,结果如图5所示。

图5 各光谱相关系数对比分析

从图5可看出,所提方法的光谱相关系数曲线极其接近理想状态值,其值保持在0.75以上,而另外三种方法则低于所提方法,表明所提方法的复原效果最好。通过实验证实所提方法提取图像光谱特征较多,从而有效保证复原图像的质量。

3.2.3 复原时间对比

实验设有200张模糊高光谱图像需要复原,分别采用二次约束、K-最近邻与PSO与所提方法对这些图像复原处理,不同方法的模糊高光谱图像复原耗时如图6所示。

图6 不同方法的模糊高光谱图像复原耗时情况

从图6中可知,四种复原方法的耗时曲线都随着图像数量增加呈上升趋势,所提方法耗时曲线上升趋势最小,而二次约束、K-最近邻与PSO方法复原耗时曲线上升趋势大致相同,且大于所提方法的上升趋势,这是因为所提方法在图像处理过程选用3D卷积复原算法,计算过程较为简单,在12.1s内就能完成200张模糊高光谱图像复原,对比方法至少需要28.7s,证实所提方法模糊高光谱图像复原性能良好。

4 结论

由于高光谱拍摄过程,拍摄设备运行导致拍摄平台振动,得到拍摄图像较为模糊,无法从图像上获得有效信息,为此,对深度学习下模糊高光谱图像复原数学模型仿真研究。通过分析高光谱成像过程,根据傅里叶变换、图像像元运动偏移情况建立其退化数学模型,利用3D卷积核提取模糊高光谱图像特征,并对其重组,得到较为清晰的图像,完成图像复原。实验结果表明,所提方法模糊图像复原效果最佳,复原的峰值信噪比在6dB以上,且复原耗时低于15s。