基于载波高斯包络模型的精密单点定位保护级
2023-10-29王吉涛许承东兰晓伟
王吉涛,许承东,赵 靖,兰晓伟
(1.北京理工大学宇航学院,北京 100081;2. 中国交通通信信息中心,北京 100011)
1 引言
近年来,随着GNSS导航服务性能的不断提高,精密单点定位(Precise Point Positioning,PPP)这一高精度定位技术逐渐成为关注热点[1],正逐步应用于智能交通系统、铁路和航海等领域。接收机自主完好性监测(Receiver Autonomous Integrity Monitoring,RAIM)作为提高定位可靠性的一种重要手段,其在PPP中的应用也受到越来越多的关注[2],[3]。
RAIM算法一般通过经验噪声模型估计观测噪声的分布情况,进而计算定位误差限值即保护级(Protection Level,PL)来评估完好性风险[4],[5]。常用的经验模型主要包括卫星高度角法[6]、信噪比方法[7]和高度角信噪比联合法[8][9]等,上述方法大都根据经验选取方差因子,利用观测噪声水平和高度角、信噪比等因素的关系建立随机模型,再在此基础上进行定位解算和完好性监测。但是在PPP实际应用中,观测噪声易受多路径效应影响,出现“厚尾”现象。针对“厚尾”现象,大多采用方差膨胀方法对观测噪声尾部包络[10][11],但是该方法对于观测噪声的分布特性估计过于保守,易造成PPP完好性监测算法的低可用性。此外,目前研究主要利用大量观测数据针对伪距噪声[12][13]或双差载波噪声[14][15]随机模型开展研究,由于载波多路径和接收机噪声(Phase Multipath and Noise,PMN)提取相对困难,直接针对非差PMN的随机模型研究相对较少。
鉴于此,本文利用三频消电离层组合观测值提取三频非差组合PMN序列,建立真实环境下的PMN分布模型,并基于灰狼优化算法求解模型参数,使得保护级计算结果更为严密,以期为PPP的应用推广提供参考。
2 PPP保护级计算框架
PPP模型通常采用消电离层(Iono-Free,IF)组合观测值消除电离层延迟误差,并利用扩展卡尔曼滤波进行定位解算[16],状态方程和观测方程分别为
Xk=Φk/k-1Xk-1+wk
(1)
Zk=HkXk+vk
(2)
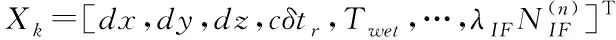
通常wk和vk为零均值高斯白噪声且互不相关,即wk~N(0,Qk),vk~N(0,Rk),Qk和Rk分别为wk和vk的协方差矩阵。Qk可由随机游走过程描述。假定各频段上码观测值和相位观测值噪声水平分别一致,则IF组合观测噪声方差与单个频段的噪声方差关系为
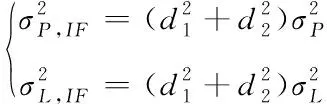
(3)
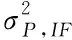
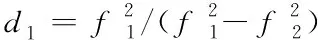
(4)
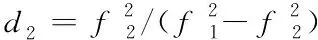
(5)
观测噪声协方差矩阵可以表示为

(6)
式中,diag[·]表示对角矩阵,n为可见星数目。
PPP定位解算的EKF方程为
(7)
完好性监测中常用保护级包络定位误差,基于特征斜率的保护级计算通常表述为[16]
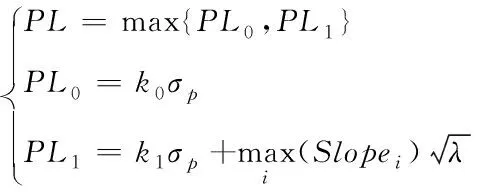
(8)
式中,PL0为无故障情况下的保护级;PL1为有故障情况下的保护级;k0和k1为放大系数,由完好性风险和连续性风险确定;σp为定位误差标准差,由Pk主对角线元素得到;λ为非中心化参数,由连续性风险、可见星数目和卫星故障概率确定;Slopei为特征斜率,用于描述检验统计量和定位误差之间的线性关系。特征斜率的计算方法为[17]
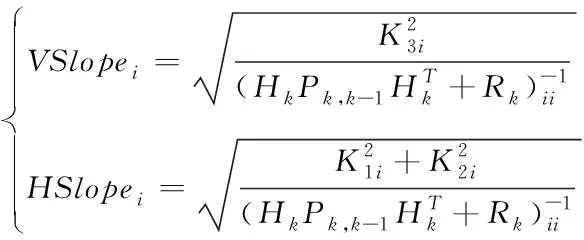
(9)
式中,VSlopei为卫星i的垂向特征斜率;HSlopei为卫星i的水平特征斜率;矩阵下标ij表示矩阵的第i行第j列元素索引。
由此可以看到,在保护级的计算过程中,特征斜率和定位误差标准差均直接或间接与Rk相关,因此载波噪声模型的精确与否直接影响完好性监测算法的可用性。
3 PMN高斯包络模型
3.1 载波观测噪声序列提取
三频载波观测值两两组合得到两组IF组合观测值,通过作差消除载波噪声以外的误差项,进而得到三频组合PMN,具体表示为[18]
LDIF=(c1L1+c2L2)-(c3L1+c4L5)
=(c1-c3)L1+c2L2-c4L5
=(c1-c3)εL1+c2εL2-c4εL5+BDIF
(10)
式中,LDIF为三频载波观测值组合;Lj(j=1,2,5)为载波观测值;BDIF为模糊度项和硬件延迟偏差;εLj((j=1,2,5)为频段j的PMN;ci(1,2,3,4)为组合系数,表达式为

(11)

(12)
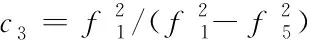
(13)
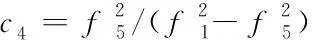
(14)
式中,f5为L5载波频率。
在无周跳情况下,BDIF为常值。通过分段区间去均值处理得到三频组合PMN序列
εPMN=(c1-c3)εL1+c2εL2-c4εL5
(15)
根据误差传播原理并基于各频段载波噪声水平一致假设,三频非差组合PMN序列噪声方差与单频载波噪声方差关系为
εPMN=(c1-c3)εL1+c2εL2-c4εL5
(16)
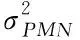
结合式(3)和式(16),通过求解三频非差组合PMN序列的噪声分布模型可以间接获得IF组合的观测噪声模型,从而实现保护级计算。
3.2 三频组合PMN分布模型
基于高度角的经验噪声模型[19]为

(17)
式中,σ0为经验噪声方差,θ为卫星高度角。对于伪距噪声,σ0=0.3m;对于载波噪声,σ0=0.003m。
该经验模型对良好环境中的观测噪声描述程度较好,但是估计较为保守,导致计算的保护级结果偏大,不符合实际情况。文献[12]提出一种可用于非高斯观测噪声分布估计的观测噪声分布模型,即
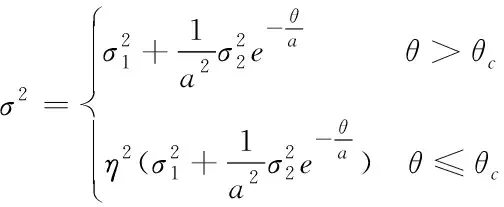
(18)

对于伪距噪声,模型中各参数取值见表1。

表1 伪距噪声模型参数[12]
本节主要在该模型基础上,利用三频组合PMN序列,求解针对载波噪声的模型参数。与伪距噪声类似,三频组合PMN由接收机噪声和多路径误差组成,其中接收机噪声与高度角无关,多路径误差与高度角指数相关,当卫星高度角高于某阈值时,PMN由高斯模型描述;当高度角低于某阈值时,PMN由高斯膨胀模型描述。PMN仍服从零均值高斯分布,其概率分布函数(CDF)为

(19)
式中,f(x;0,σ2)表示均值为0,方差为σ2的正态分布概率密度函数。
3.3 模型参数求解
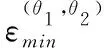

(20)
这样,不同高度角区间内PMN的真实CDF可以用频数近似描述为

(21)
式中num(·)表示对应高度角区间中PMN的统计数。
所有高度角区间对应PMN的实际CDF用矩阵形式描述为

(22)
类似地,由式(19)确定的PMN的理论CDF用矩阵形式描述为

(23)
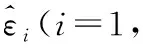
由4个模型参数确定的理论CDF和实际CDF应当保持一致,即
ΔF=-F=0
(24)
由此建立优化求解问题为
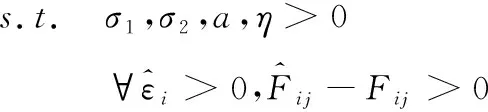
(25)
满足式(25)的σ1,σ2,a,η即为理论上的模型参数组合。该目标函数中含有正态分布函数,该问题是典型的多维非线性优化问题,采用一般线性优化方法很难保证求解结果的正确性和计算效率。因此,为快速获得准确的PMN模型参数,本文基于灰狼优化算法[20](Grey Wolf Optimizer,GWO)并结合蒙特卡洛方法实现参数优化求解。GWO算法是一种新型群智能优化算法,通过模拟灰狼群体在捕食过程中的觅食行为实现目标优化。在GWO算法中,狼群由高到低排序为α,β,δ,ω4个等级,其中α,β,δ灰狼等级最高,其位置向量表示3组帕累托最优解,ω灰狼位置根据α,β,δ更新,狼群通过等级更替实现最优解的搜索,更新过程如下
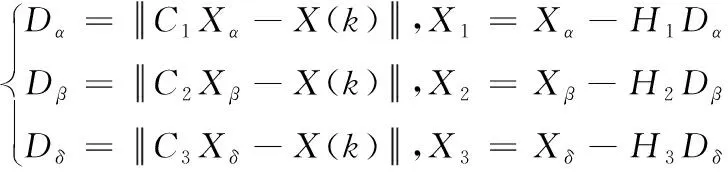
(26)

(27)
式中,t为当前迭代次数;Xα,Xβ,Xδ分别为α,β,δ狼个体位置向量;X表示ω狼个体的位置向量;D表示狼个体与最优解的距离;C和H为权重系数。在迭代过程中,C和H根据如下规则更新
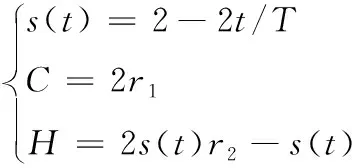
(28)
式中,T为最大迭代次数;r1,r2为[0,1]随机数。
本文中,X为PMN分布模型参数,即
X=[σ1,σ2,a,η]
(29)
本文将GWO算法应用到PMN分布模型参数的求解当中,通过对4个模型参数的快速寻优,以达到提高模型求解准确性和高效性的目的。基于GWO算法的模型参数求解流程如图1所示。具体实现过程包括以下步骤:
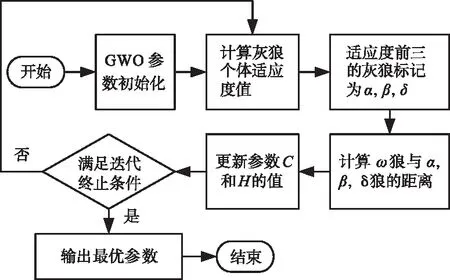
图1 基于GWO的模型参数求解流程
1)对PMN序列进行高度角和数值区间划分,统计各区间PMN样本频数,建立实际CDF矩阵。
2)初始化灰狼种群数量M和最大迭代次数T等参数,设置参数σ1,σ2,a和η的取值范围,选择式(25)作为适应度函数。
3)计算狼群个体位置及其适应度。
4)遍历灰狼种群,计算所有个体适应度函数,将适应度函数值排序前3位的灰狼个体标记为α,β,δ。
5)根据式(26)(27)计算ω狼与α,β,δ狼的距离,并更新α,β,δ狼的位置。
6)根据式(28)更新算法中参数C和H。
7)判断是否达到最大迭代次数T,若达到则保存最优组合优化解Xα,即模型参数的最优值,否则返回步骤4)。
4 仿真分析
选取JFNG站100天(2020年1月1日至4月9日)的观测数据,接收机型号为Trimble NetR9,天线为“TRM55971.00”,采样率为30s。由于GPS卫星目前只有Block ⅡF类型卫星具有三频观测数据,因此只提取该类型卫星的PMN序列,观测数据总量为1.04×106,可以用于高度角阈值和模型参数的确定。
4.1 高度角阈值确定
PMN在不同高度角范围具有不同的噪声水平,利用Q-Q Plot方法、峰度和偏度系数对PMN的高斯特性进行分析。以G32卫星为例,按照高度角间隔Δθ=5°将PMN序列从0到90°划分为18组,绘制PMN噪声序列在10°~15°,20°~25°,45°~50°和60°~65°四个高度角区间内的Q-Q Plot图,如图2所示。
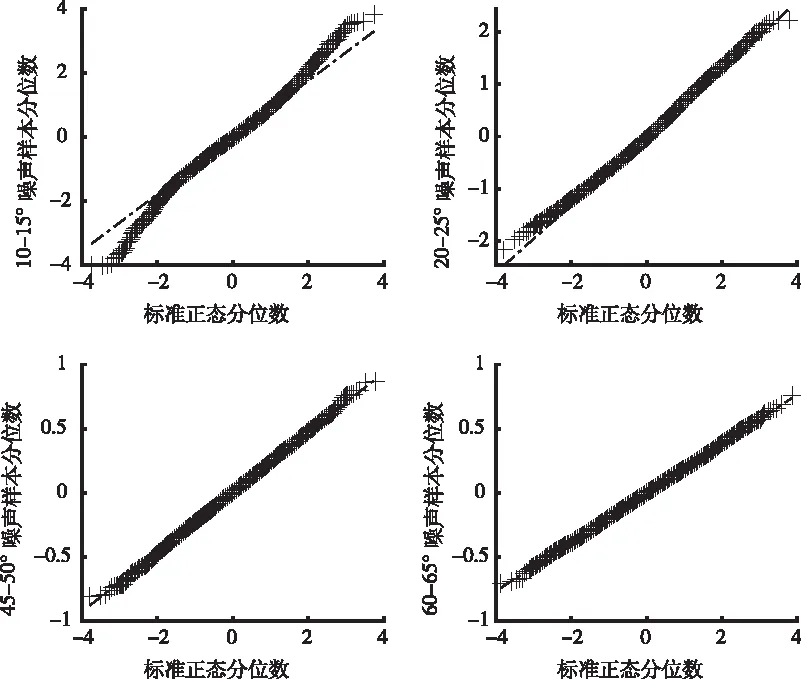
图2 载波噪声Q-Q Plot
从图2中可以看到,GPS卫星在高度角较大情况下的PMN序列完全符合高斯分布,但在10°~15°小高度角区间下,PMN序列基本符合高斯分布,但是在“尾部”与高斯分布存在偏离。
为检验PMN序列的对称性和“厚尾”情况,分别计算卫星在不同高度角区间的偏度值和峰度值,结果如图3所示。可以看到,各高度角区间中载波噪声对应的偏度始终在零值附近波动,说明PMN序列的分布具有对称性,高度角的变化对PMN偏度影响较小。在0~20°高度角区间内,PMN峰度值显著大于3,PMN序列的分布具有尖顶和“厚尾”特征;在大于20°高度角区间中,PMN峰度值趋于一致,近似为3,说明基本服从高斯分布。

图3 载波噪声的偏度和峰度值
不同高度角下的载波噪声QQ-Plot、偏度和峰度值表明,应分段描述不同高度角区间的噪声分布特性,这进一步验证了PMN分布模型的合理性,并可确定高度角阈值为20°。当高度角大于20°时,高斯分布对PMN的分布描述效果较好。但当高度角小于20°时,PMN分布呈现厚尾特性,若仍用高斯分布描述其分布特性,与实际情况不符,因此采用膨胀系数η进行高斯包络。
4.2 模型参数求解
将每组高度角区间中的PMN序列从小到大排列后划分为200个子区间,高度角阈值取为20°。为削弱GWO算法不同初值选取对参数优化结果的影响,采用蒙特卡洛方法进行多次计算,蒙特卡洛次数设为50,取最优估计结果,得到各卫星模型参数估计值,如图4所示。
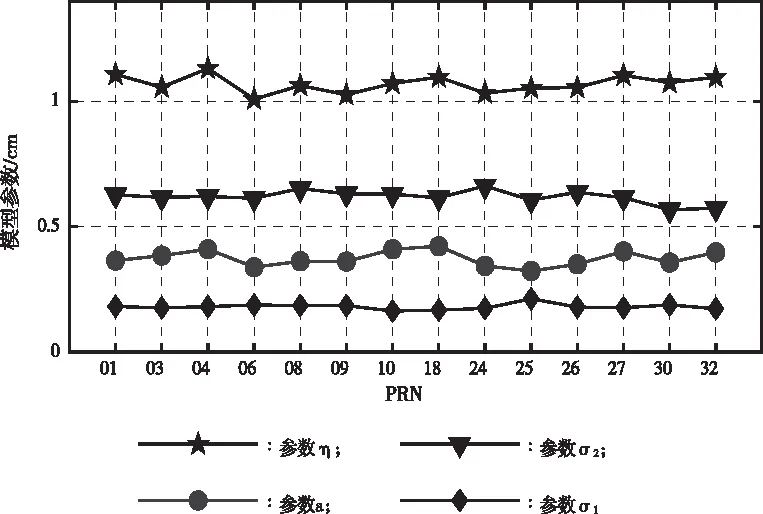
图4 模型参数估计结果
通过比较可以发现,各卫星的PMN分布模型参数基本一致,取各卫星模型参数的平均值作为最终结果,得到三频组合PMN的分布模型参数,并由式(16)得到单频PMN模型参数,具体结果见表2。
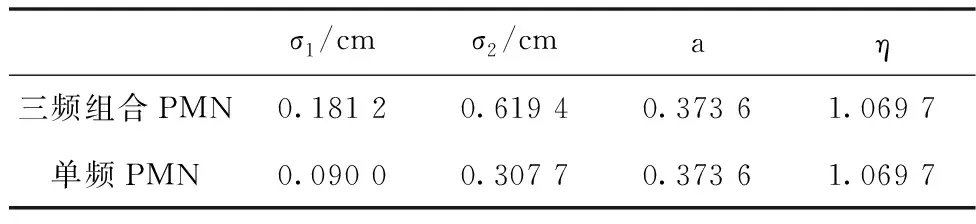
表2 PMN模型参数
4.3 观测噪声包络分析
为验证所求模型参数的有效性,采集一组实测数据并提取三频非差组合PMN序列,观测数据信息见表3。分别利用经验模型和PMN分布模型对载波噪声进行3σ包络分析,结果如图5所示。
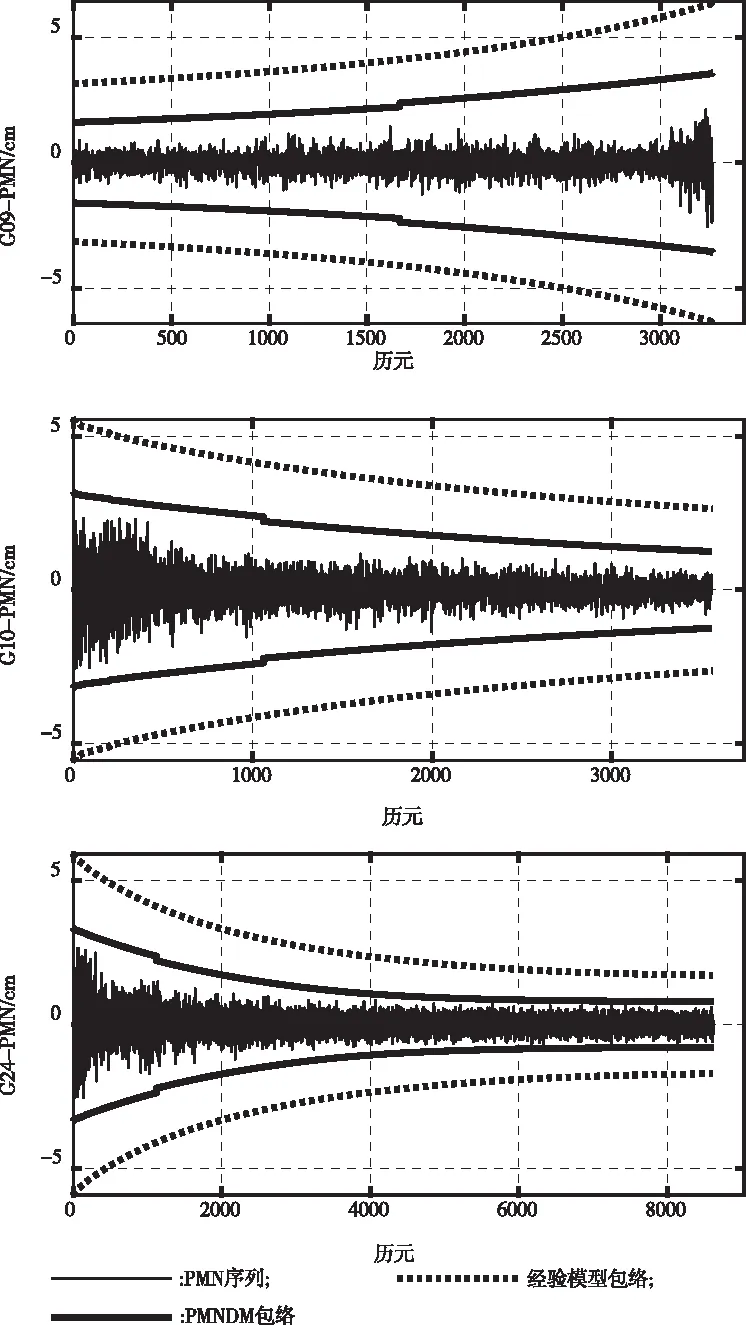
图5 两种模型噪声包络情况

表3 观测数据信息
提取所有卫星在5°~20°和45°~60°高度角区间中的三频组合PMN序列,对比经验模型和PMN分布模型在低高度角和大高度角两种情况下对载波噪声概率密度的包络情况,结果如图6和图7所示。

图6 低高度角噪声模型概率密度包络
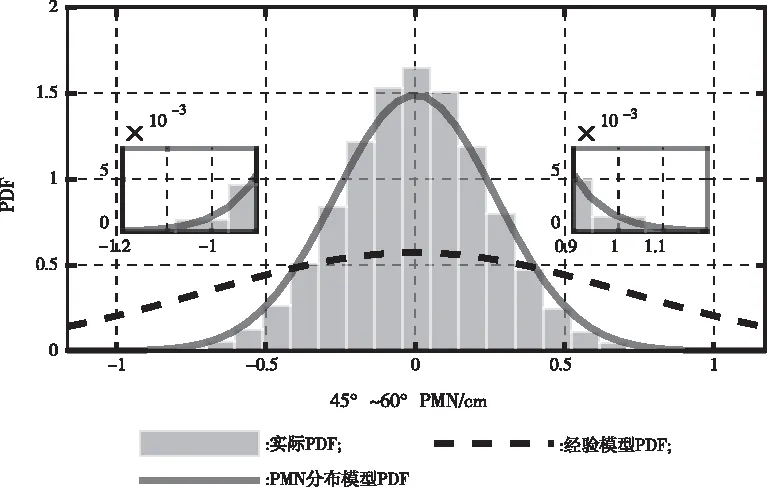
图7 大高度角噪声模型概率密度包络
结合图5、图6和图7结果可以发现,两种模型均能对载波噪声进行包络,但是经验模型对PMN的噪声分布情况估计明显过于保守,与经验模型相比,PMN分布模型的包络曲线与真实PMN贴合更加紧密,对载波噪声包络效果更好。
4.4 保护级结果评估
为进一步验证所提载波噪声模型在PPP完好性监测中的性能,选取机载动态观测数据进行保护级计算。观测时长约为30分钟,采样率为1 s,接收机类型为“NovAtel OEM7”,卫星天空图和飞行轨迹分别如图8和图9所示。

图8 卫星天空图

图9 载体飞行轨迹
动态定位解算模式采用IF组合PPP浮点解,卫星轨道和钟差采用IGS改正产品改正,对流层误差等采用模型改正,卫星截止高度角设置为7°。两种随机模型方案包括:①式(17)所示的经验噪声模型②本文所求解的载波噪声模型。用于计算保护级的完好性参数设置见表4。

表4 完好性参数设置
图10和图11展示了两种随机模型方案的定位误差和保护级计算结果。可以看到PMN分布模型对应的VPL和HPL始终小于经验噪声模型,VPL值最大相差1.13 m(第1794历元),HPL值最大相差0.45 m(第1789历元)。

图10 垂向保护级和定位误差

图11 水平保护级和定位误差
两种保护级收敛后的统计信息见表5。与经验噪声模型相比,PMN分布模型的VPL平均降低了38.1%,HPL平均降低了27.1%,说明后者模型更加精确,克服了经验模型保护级计算结果偏保守的缺点。
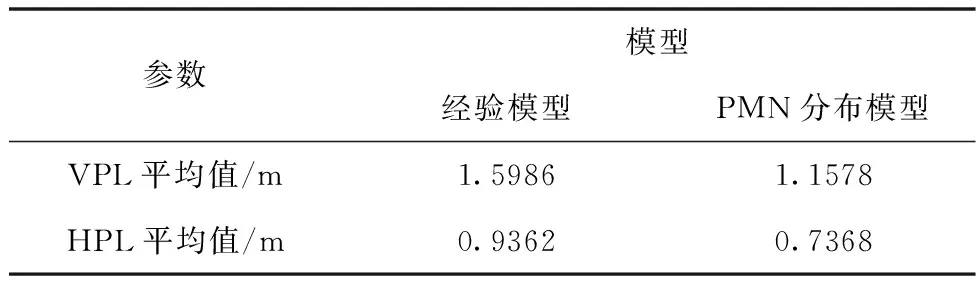
表5 保护级的统计信息
5 结论
为解决经验噪声模型计算精密单点定位保护级具有保守性的问题,本文基于GWO算法求解了一种载波噪声分布模型。仿真结果表明,相比于经验观测噪声模型,文中所提PMN分布模型对于载波噪声的分布描述更为精确,使精密单点定位的垂向保护级降低了38.1%,水平保护级降低了27.1%,提高了完好性监测的可用性。
