车辆驾驶环形轨迹人机交互导航仿真模型研究
2023-10-29崔俊杰张卫正
崔俊杰,张卫正
(1. 郑州轻工业大学,河南 郑州 450002;2. 郑州轻工业大学计算机与通信工程学院,河南 郑州 450002)
1 引言
当前国民经济快速增长,私家车数量与日俱增,导致城市交通情况逐渐恶劣,交通事故率呈递增状态。为了缓解道路拥堵状况,规划出众多环形立交桥起到一定的分支车流作用,但环形路线没有临时更改路线的调整空间。因此在车辆驾驶过程中,如何帮助用户挑选出最优路线,从根本上提高行驶效率已成为当前该研究领域的主要课题之一。
制造商在生产汽车时,每辆车内都安装了智能导航设备,导航会根据交互指令,提供给驾驶人员从出发点到目的地的行驶路线。一般情况下导航系统可被划分成主机和显示终端两个部分,运行导航程序时,内置卫星导航天线根据传输的卫星数据,即可给出该车辆的详细位置,随后导航主机将位置数据放置到地图数据中进行匹配,根据人机交互指令将车辆当前信息显示在终端,便于后续导航。车辆导航的路径规划问题就是在导航地图上找到从起点到终点的最佳路径。在实际应用中,当交通路况发生变化时,最佳路径搜索也应该发生变化。驾驶人员不仅可以利用车辆导航技术获得最终目的地位置,还可实时了解最优路线的路况信息。
为此,本文提出车辆驾驶环形轨迹人机交互导航仿真模型研究,首先采用D-S证据理论(D-S Evidence Theory)构建一个非空集合识别框,判定当前车辆的基本行驶方向,通过地图匹配算法确定当前车辆位置信息;其次利用Dijkstra(迪克斯特拉算法)计算最短距离路径,对导航模型中的路线进行规划,最后利用无迹卡尔曼滤波(UKF)对数据信息进行融合处理,完成最终导航。
2 驾驶车辆定位

行驶环形轨迹是一个连续过弧的路程,所以必须到达目前节点才能到下一个路段,因此针对环形人机交互导航模型来说,提取匹配路线时,需要结合历史数据,从根本上提升匹配精度,减少模型匹配计算量。本文采用D-S证据理论构建一个非空集合识别框,便有
U={A1,A2,…,An}
(1)
式中,Ai(1≤i≤n)代表当前车辆在i号路线上行驶。集合中所有元素之间都相互排斥,根据证据理论判定当前车辆行驶方向[2,3],并将其作为原始证据。考虑到GPS定位可能存在的误差,便将详细的位置信息描述为
di=[l1(l2+l3+l4+l5)]/5
(2)
式中,di表示置信椭圆在第i条路线上的位置信息,l1代表椭圆中心点在该路线上的实际投影距离,而l2、l3、l4、l5则分别表示椭圆轴的端点,在第i条路线上的投影距离,当距离取值为0时,可得知li取其中最小值。
假设用m1描述位置信息证据在U上的mass函数,可得出
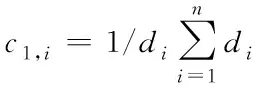
(3)
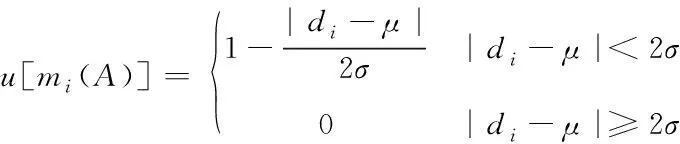
(4)
c1,i与m1、m2一样,为mass函数中特指向量,μ表示证据距离特征。
将m1和m2融合成为一个mass函数m得出

(5)
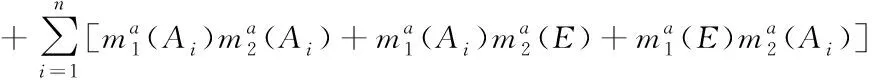
(6)
3 车辆驾驶环形轨迹路径规划
在导航中输入最终目的地,交互指令会立刻给出到达该地的多条路线,有的路线是避开红绿灯,有的路线是避开高峰堵车路段,而车辆路径规划会在最大程度上提高车辆的行驶效率,选择最优路线[4-7]。
本文利用Dijkstra算法对导航模型中的路线进行规划,计算步骤如下:
假设有带权有向图为G=(B,E),其中B表示包括n个节点的数据集合,E代表存有m条弧的集合,(y,b)是E集合中从y到b的弧线,W(y,b)的弧(y,b)的正权值,那么将节点划分为两组,第一组是已经确定了是最短距离的节点集合S,原始状态为集合中仅有一个起始源点b0,第二组是不确定是不是最短距离的集合(B-S),计算过程中每算出一个最短距离路径b0,就将bk转至S集合中,直到所有节点都是最短距离为止。
将di(1≤i≤n)作为目前所找到的从源点b0到其它节点bi的最短路径长度,如果从b0到bi之间有环形路径,那么di为弧(b0,bi)的权值,反之没有则令di为∞。
假设第一条最短路径为(b0,bj),那么j则满足
dj=min{di|bi∈B}
(7)
上述计算得知,下一条最短路径终点即为(b0,bk),或是(b0,bj,bk)。
根据上式计算结果可知,假设S是已经计算出的最短距离集合,那么下一条路经的节点则是S集合中的节点之一,长度计算式便有
dj=min{di|bi∈B-S}
(8)
经过多次最短路径计算后,终点bj最终也转至S集合中,然后对所有的节点进行bi∈B-S计算,更新di有
di=min{di,dj+W(bj,bi)}
(9)
根据上式可计算出对应集合中源点b0到所有节点的最短距离,如图1所示,其中图1(a)为带权有向图,(b)表示集合中源点b0到其它点的距离显示图。
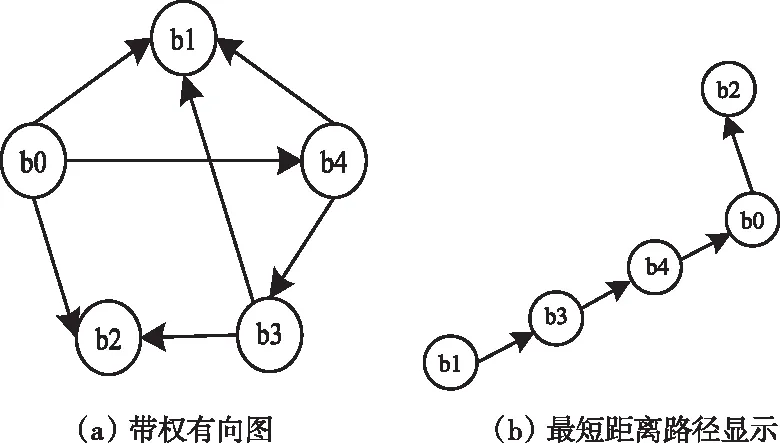
图1 最短距离路径树
其中详细的算法描述如下:
步骤一:将集合中节点划分为三个部分,表示为d(b)、k(b)、p(b),已知d(b)是集合S中所有节点的最短距离,k(b)便表示为其中任意变量(布尔型),用来表示节点b的最短路径是否求解出,p(b)是b的后继节点指针。将三个信息量初始化计算便有

(10)
步骤二:扫描k(b)=false的所有节点,从集合中挑选出一个有最小路径长度的节点b,得出:
d(b)=min{d(bi)|k(bi)=false,bi∈B}
(11)
式中,k(b)=true。
步骤三:对k(w)=false且邻接于节点b的节点w进行监测,如果满足d(w)>d(b)+W(b,w)条件,可描述为
d(w)=d(b)+W(b,w)
(12)
步骤四:反复计算步骤二、三,直到得出k(E)=true;
步骤五:由E开始遍历后继节点指针p直至源点S,即获得S到E的最短距离路径,便有
PSE={b0=S,b1,…,bk=E}
(13)
其中,bi=p(bi+1),i=0,1,…,k-1。
4 人机交互导航仿真模型构建
利用无迹卡尔曼滤波(UKF)对最优路径信息进行融合处理,完成最终导航。计算车辆的状态和对应误差协方差矩阵初始值[8]
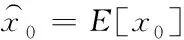
(14)
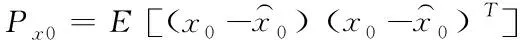
(15)
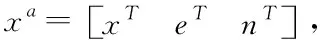

(16)
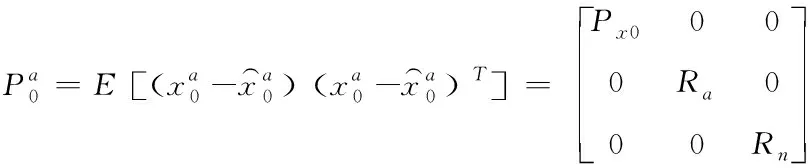
(17)
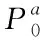
模型中的所有数据节点都具有周期性[9],每个周期含有Sigma点计算、状态更新、观测更新的三个主要流程,计算时根据上一周期所得的车辆轨迹、状态等信息,做对应的模型估计,将所有信息进行融合,得出新的估计取值和导航模型的误差协方差矩阵[10-13]
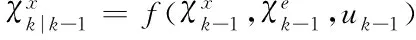
(18)

(19)

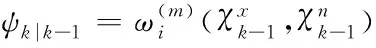
(20)

5 仿真研究
为验证本文算法是否能在环形驾驶中快速安全完成导航,首先对环形轨迹安全车速进行测试,以确保车辆在环形道路中能够安全行驶。实验中位移单位为米,单位时间为秒,速度单位为m/s,加速度单位为m/s2,环形弧度用(red)表示,其中观测噪声协方差取值为10-3I,数据采集周期T以及缩放因子k取值分别为0.02、0。本文仿真环境参照重庆某天的下午4点22分,从大龙山公园到玉祥门,此时交通路况处于下班高峰期,路况较为复杂且多变。车辆参数如表1所示
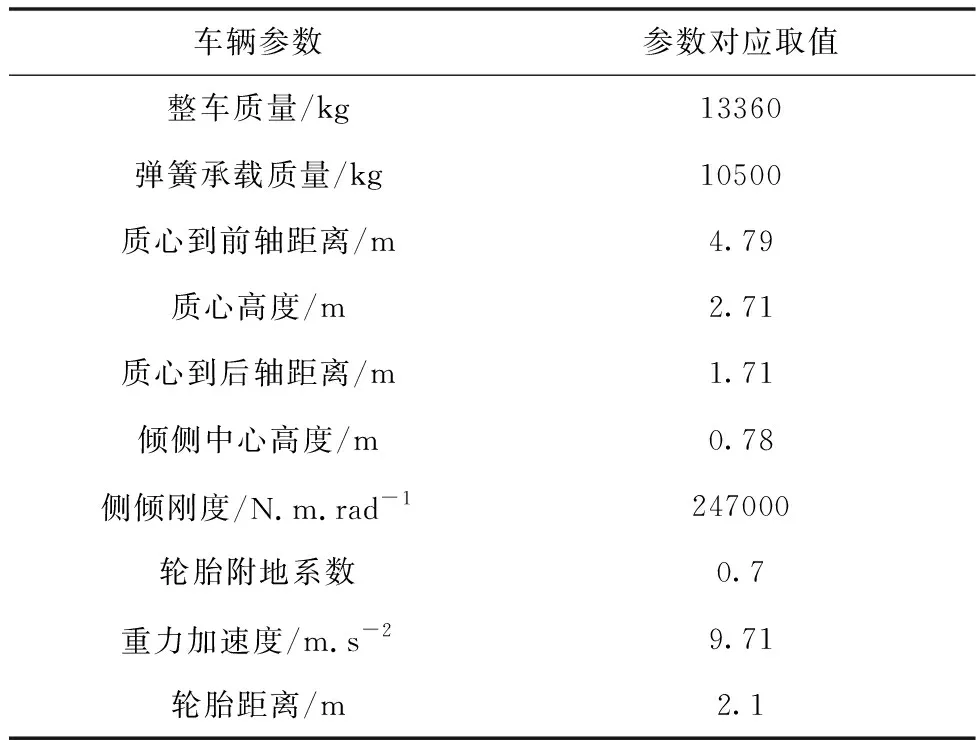
表1 车辆仿真参数
5.1 环形轨迹安全车速测试
车辆在环形轨迹中,当车速处于导航推荐的最高车速以内时,车辆质心侧偏的角度就为0,此时车辆转向角度为完全理想取值,如图2所示,车辆正常速度行驶会出现在理想轨迹或内侧滑轨迹,内侧滑轨迹照比外侧滑轨迹来说是相对安全的,因此内侧滑轨迹可以称之为期望取值,反之如果车速过快导致外侧滑,便可能出现侧翻等危险,为此本文得出了环形轨迹的安全车速公式

图2 环形轨迹转向侧滑
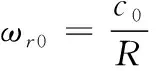
(21)
式中ωr0代表理想的环形角速度,c0则被描述为车辆在理想轨迹运动下的转向行驶速度,R代表质心偏向角。
结合实际环境信息,根据式(21)计算出车辆过弯的安全期望车速以及转向角,以期望速度作为衡量车辆出现侧滑阈值的标准,当车辆在环形轨迹中行驶时速度峰值高于期望转向角时,即判定为不安全车速[15],及时通过可视化界面提醒驾驶人员。
5.2 人机交互导航效果分析
图3为导航结果。该车辆的轨迹数据包括了高架桥和将近一半道路网络,并且网络中含有多个环形路线。
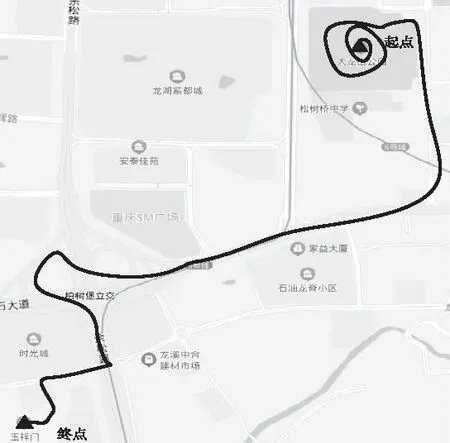
图3 最佳导航轨迹示意图
从图3中标记路线为大龙山公园到玉祥门的最佳路线,可知方法能根据实时路况给出相应的导航路线,在路况轻松的时间段需13分钟路程,全程3.5公里、有3个红路灯,路经柏树堡立交、松石大道等主干路,但因松石大道下班高峰期时,路况较为紧张会出现相应的交通堵塞,并不能顺畅通过,所以在D-S证据理论基础上计算轨迹序列的备选路线集合,进行路线分段。
图4中标注出了轨迹序列的备选路段集,通过交互指令在终端显示,备选路线较为轻松路况需要14分钟路程,全程3.9公里、途经9个红绿灯,路经龙山立交、余松路。备选路线仅比最佳路线多0.1公里,可以避免松石大道交通堵塞,但多了6个红绿灯,车辆驾驶中需要用户自己抉择。说明本文导航模型可完全避免导航失误的同时,具有较高的智能实用性。
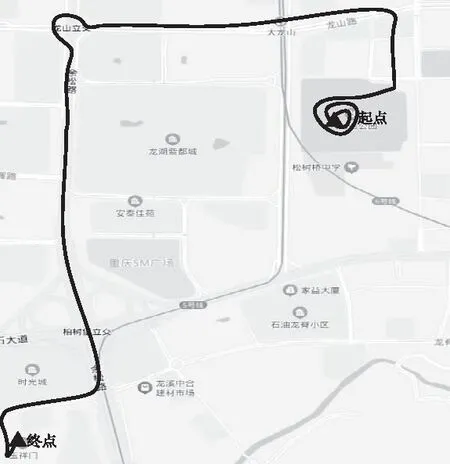
图4 车辆导航模型备选轨迹
6 结论
为缓解拥挤的城市交通道路网行车压力,本文提出车辆驾驶环形轨迹人机交互导航仿真模型研究。首先利用地图匹配算法,确定当前车辆位置信息,其次根据不同长度的路径节点,构建Dijkstra最短距离路径,规划车辆驾驶路线,最后通过无迹卡尔曼滤波对数据信息进行融合处理,完成最终导航。
