结构优化视域下《新思路数学》教学实验探究
——以七年级上册第二章“代数式”为例
2023-10-28李思颉杨花朱家正张嫌
李思颉 杨花 朱家正 张嫌
一、 引言
李尚志教授主编的读本《新思路数学》是张景中院士教育数学思想物化的产物,该读本于2020年出版。我校有幸参与到读本《新思路数学》的教学实验研究中,如何在当下“减负”的时代背景下将实验教学更好地与常规教学进行融合,并符合2022年版义务教育数学课程标准?文章依据以上问题,在结构优化视域下对《新思路数学》教学实验进行探究,并以七年级上册第二章“代数式”为例,从教学实验背景、读本知识架构、读本对教学的优化作用等方面进行阐述。
二、 《新思路数学》的教学实验背景分析
(一)问题的提出
数学作为基础教育阶段的重要学科,因其学科内在特点,学生的学习并不容易。如何学好数学,一直是困扰教师和学生的问题。如何改造数学使其更适宜于我们的教学和学习?把难学的数学变容易,成为张景中院士长期的研究目标。1989年他提出了介于数学和教育学之间以数学为主的交叉研究方向——教育数学,努力为每个难点寻找简单路径,从而让数学变得更容易,让更多的学生对数学感兴趣,树立起学好数学的自信心。
教育数学发现了三角在小学数学知识基础上的生长点,提出用面积关系定义正弦,实现了国际上著名的数学教育大师弗赖登塔尔提出的“提前两年学正弦,让数学能配合物理进度”的设想,此研究始于1974年,1980年研究成果发表,2012年正式进入整体全学段教学实践。2020年由北京航空航天大学数学与系统科学学院李尚志教授主编的读本《新思路数学》出版,标志着教育数学教学实践载体的诞生。
(二)现实的意义
《义务教育数学课程标准(2022年版)》中指出课程目标要以学生发展为本,以核心素养为导向,进一步强调学生获得数学“四基”“四能”,形成正确的情感、态度和价值观。而基于教育数学思想编写的读本《新思路数学》,通过把难的知识变容易,探索学生学习的特点和规律,使学生能得到全面的发展,利于核心素养的落实,对推动初中数学教育的改革具有重要意义。
新课标指出:“课程内容的组织,重点是对内容进行结构化整合,探究学生核心素养的路径,重视数学结果的形成过程,处理好过程与结果的关系。”提出了结构化教学理念。《新思路数学》不仅限于对数学教材进行教学法加工,更致力于对数学本身进行再加工、再创造,增强了知识间的联系性与整体性,让逻辑性更加突出。
三、 《新思路数学》的知识架构分析
在教学实验中,《新思路数学》读本的知识架构与人教版存在差异,下面将以七年级上册第二章“代数式”为例进行分析。
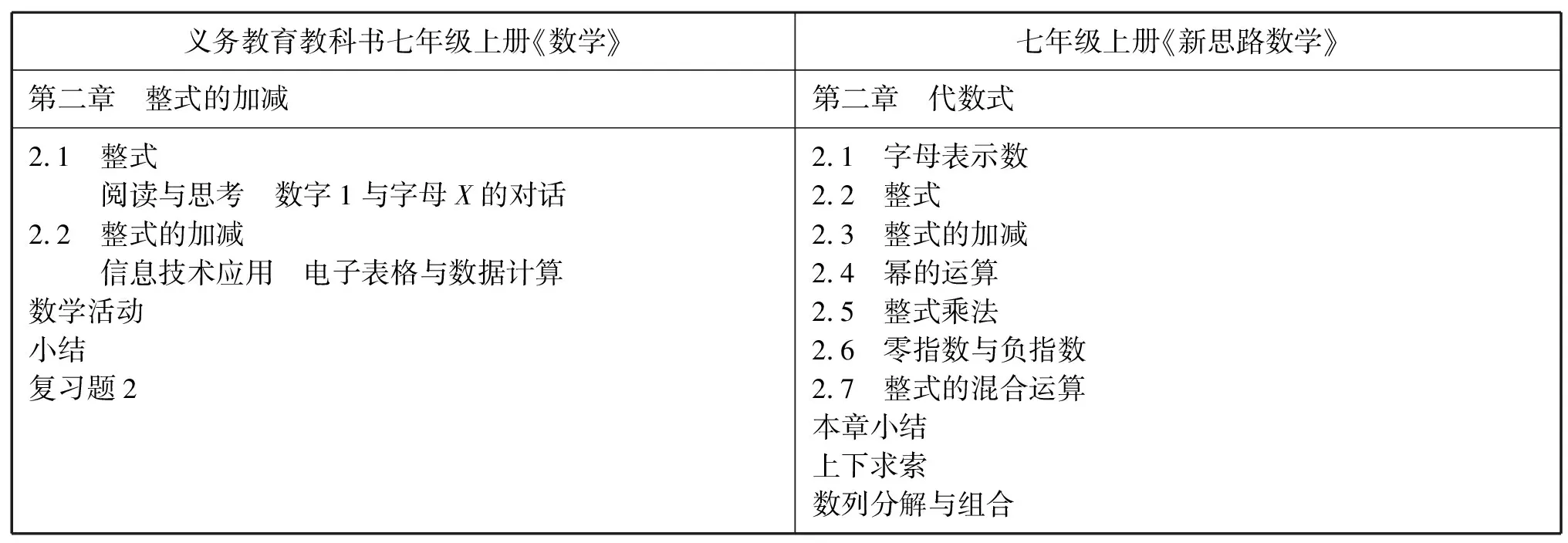
义务教育教科书七年级上册《数学》七年级上册《新思路数学》第二章 整式的加减第二章 代数式2.1 整式阅读与思考 数字1与字母X的对话2.2 整式的加减信息技术应用 电子表格与数据计算数学活动小结复习题22.1 字母表示数2.2 整式2.3 整式的加减2.4 幂的运算2.5 整式乘法2.6 零指数与负指数2.7 整式的混合运算本章小结上下求索数列分解与组合
第一节“字母表示数”是全章的开篇,读本从五个方面来阐述了用字母表示数的优势:“字母运算识破玄机”“字母才能算无穷”“规律指挥案例”“字母表示公式”“字母表示运算律”。通过五个具体的案例学生能够感受到字母的神奇魔力,从而为本章的学习创造良好的兴趣基础。
第二节“整式”内容与人教版的基本一致,但知识点的引入顺序不同。人教版从“单项式”“多项式”,最后得到“整式”的概念,其逻辑结构按“分-总”式来展开。而《新思路数学》按照“整式”“单项式”“多项式”的顺序来阐述,是从总体到局部的逻辑结构。
第三节“整式的加减”与人教版相比增加了更多的探究内容,除了“合并同类项”“去括号”“求代数式的值与基本概念”,还增加了“探与究 探索与验证规律”“恒等式与面积”两个项目式探究问题,其中“探与究 探索与验证规律”揭示了找规律的基本方法,而“恒等式与面积”为之后整式乘法的几何意义奠定了基础。
第四节“幂的运算”、第五节“整式乘法”是人教版八年级上册第十四章“整式的乘法与因式分解”的内容,而第六节“零指数与负指数”对应人教版八年级上册第十五章“分式”中整数指数幂,以上内容都提到了七年级上册来完成,缩短了知识学习的跨度。
第七节“整式的混合运算”将初中阶段整式的所有运算综合起来,并对分式的引入埋下了伏笔。
“上下求索”是读本中的特别之处,本章的“上下求索”是探究“数列分解与组合”,利用“平方数列巧分解”和“猜数列不靠谱”两个问题,深入探究数列的分解与组合,其中高中数学思想方法的渗入为今后的学习做好铺垫。
以上分析不难发现,《新思路数学》读本在第二章“代数式”的内容上进行扩充与整合,体现从数到式逻辑思维的逐级递进;结构上进行优化,体现大单元教学设计的整体思想。因此《新思路数学》读本利于教学整体结构的优化,增加了知识链接的紧密性,使数学变得更容易。
四、 《新思路数学》教学优化分析
(一)《新思路数学》利于内容结构优化
对比人教版,《新思路数学》在内容结构上进行了系统的优化。第二章“代数式”在人教版的基础上增加了“幂的运算”“整式的乘法”“零指数与负指数”“整式的混合运算”,将整式的部分内容前置,并统一编排到一个章节,实现以大概念为抓手,帮助学生从整体上来理解整式的运算结构,促进学生能够自主构建知识体系,实现知识之间的迁移与应用,落实学生的数学核心素养。此外,在“上下求索”中增加了“数列分解与组合”,为做好初高中的衔接打下坚实的基础。
(二)《新思路数学》利于逻辑结构优化
《新思路数学》不仅致力于对内容结构优化,还在逻辑结构上进行了优化,呈现更简单的逻辑结构认知。
新思路“代数式”的第一课时是字母表示数,而人教版并没有单独的章节呈现。新思路以字母的引入,实现小学算式到初中代数式的过渡,通过“字母运算识破玄机”“字母才能算无穷”“规律指挥案例”“字母表示公式”和“字母表示运算律”五个有趣的案例,充分说明了字母表示数的优越性,使学生体会从具体到抽象的认识过程,发展符号意识,感受“抽象”的数学思想。以“字母运算识破玄机”为例:
(手机号码泄露你的年龄)有人设计了一个算法,用你的手机号码算出你的年龄。
算法如下:将你的手机号码加20,乘25,再乘4,再加23,再减去你的出生年份。末两位就是你的年龄。
解:设你的手机号码为a。加20等于a+20。
乘25得25(a+20)=25a+500(分配律)。
再乘4得4(25a+500)=100a+2000(分配律)。
再加23得(100a+2000)+23=100a+(2000+23)=100a+2023(加法结合律)。
下一步减去你的出生年份。因为每个人的出生年份不同,不能用一个固定的数表示,因此只能用字母表示。出生年份与手机号码无关,不能再用a表示,可以用与a不同的任意字母表示,比如用b表示,得到100a+2023-b。
100a是手机号码这个整数a的100倍。不论a是多少,100a的末两位都是00,对计算末两位不起作用。因此,100a+2023-b的末两位就是2023-b的末两位,与a无关。知道了出生年份,理所当然就知道了年龄,没有任何神秘之处。字母运算这个很简单的科学知识将它解释得清清楚楚,根本不是“科学不能解释”。所以字母运算利用运算律解答问题,就是用最大的规律来得出这个问题的小规律。
除此之外,在“字母表示公式”这部分内容中,用字母表示圆的面积时,对为什么要用π来表示进行了解释说明。因为圆周率是无限不循环小数,写得太少精确度不够,写得再多也不能完全表示圆周率,为了方便起见,专门用一个字母π代表它的精确值,能更好地让学生认识到用初中阶段π与小学的不同之处!
可见《新思路数学》体现了从数到式逻辑思维的逐级递进,揭示了从数到式学习的必要性,让数学从真正意义上变得容易。
(三)《新思路数学》利于情境创设优化
新课标强调:“加强知识学习与学生经验、现实生活、社会实践之间的联系,注重真实情境的创设,增强学生认识真实世界、解决真实问题的能力。”有效的情境创设能够激发学生学习的主动性和积极性,不仅有利于营造高效的初中数学教学课堂,拓展学生的数学思维,还有利于发展学生的数学核心素养,达到全面育人的目的。
新思路在情境创设上也给我们提供了很好的借鉴。这里以“去括号”法则教学为例,以“几何图形求面积”为情境作为“去括号”的导入:如图1所示,长为am,宽为bm的长方形铁片,四角上剪去边长为xm的小正方形,且在中央部分又剪去边长为ym的小正方形。求这块铁片剩下的面积。
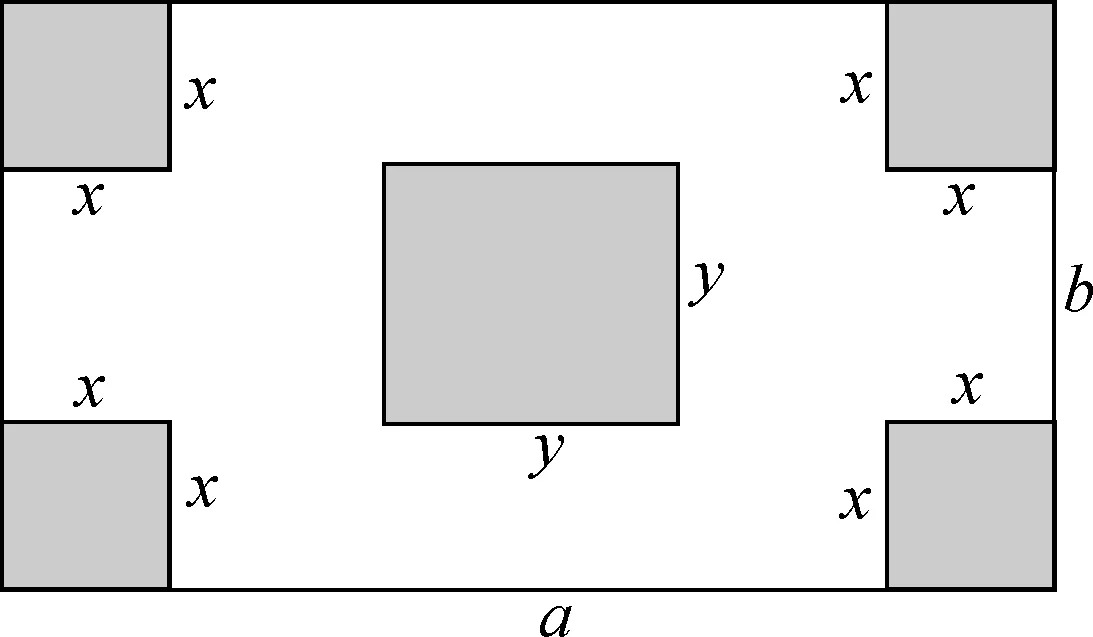
图1
首先,要表示铁片剩下的面积,有如下两种方法:
解法一:铁片剩下的面积=铁片原来的面积-剪去的总面积
即,铁片剩下的面积=ab-(4x2+y2)。
解法二:铁片剩下的面积=铁片原来的面积-四个角边长为xm的小正方形的面积-中央部分边长为ym的小正方形的面积
即,铁片剩下的面积=ab-4x2-y2。
学生通过不同的方法表示铁片剩下的面积,最终得到ab-(4x2+y2)=ab-4x2-y2。
通过让学生观察等号的左右两边,发现去掉括号与括号前面的“-”号时,括号内各项全变号,使学生对“去括号”有了初步的感知,再通过运算律进行说理。这样的情景创设优化设计,不仅激发学生的学习动机,而且增强了学生的学习动力,使学生从中享受到整个学习过程带来的乐趣,从而揭示“去括号”的本质,让深度学习有效发生。
(四)《新思路数学》利于习题设计优化
习题设计是日常教学的重要组成部分,不仅可以检查学生对知识点的掌握情况,而且还可以促进学生基本技能的形成。精巧的习题优化设计,能够使得不同层次的学生在数学上得到不同的发展,有效提升了学生的数学核心素养。
《新思路数学》在习题设计上坚持素养导向,注重学生素养能力的提升。在“整式的加减”这一节中加入了“探索与验证规律”,设计了以“火柴棒搭正方形”为背景的习题:如图2所示,用火柴棒从左到右搭若干个同样大小的正方形(搭一个正方形需要四根火柴棒),回答下列问题:

图2
(1)第一个正方形需要补充几根火柴棒,才能得到第2个正方形?(2)前两个正方形需要补充几根火柴棒,才能得到第3个正方形?(3)前(n-1)个正方形需要补充几根火柴棒,才能得到第n个正方形?(4)搭10个正方形需要多少根火柴棒?(5)搭n个正方形需要多少根火柴棒?(6)搭100个方形需要多少根火柴棒?
此习题设置了由易到难,由特殊到一般的问题串,让学生学会观察、分析,通过特殊的问题来归纳总结出一般规律,立足核心素养,将“探”与“究”紧密结合,一方面让学生利用字母运算,从已有的可靠规律推出新规律(3n+1);另一方面学生也可以从数据的来源去寻找规律,在本题中数据来源是火柴搭成的正方形,就保证了每增加1个正方形需要增加3根火柴。这样的习题设计优化使学生的思维能力、自主探索能力和创新能力得以培养与发展。
此外,在本节中还增加了以“数列中的裂项相消法”和“求数列的前n项和”为背景的习题,选取学生能借助新知识解决“跳一跳能够到”的问题,给足其探究空间,将高中的内容在初中适当渗透,为学生后面学习高中的知识与方法奠定了基础,充分体现了教育数学“一线串通”的思想。
五、 结论
在“代数式”章节的精细解读和教学实践研究中,可以发现《新思路数学》的部分内容设计虽然理解起来有一定难度,但是不可否认,其中一些章节内容的调整与呈现,都值得我们思考和借鉴。并且从读本的案例中可以看出,《新思路数学》所提供的内容体系呈现出严谨的逻辑与透彻的诠释,很好地揭示了数学的本质,值得我们在教学中深入研究和继续推进。同时《新思路数学》读本在整体结构优化、内容结构优化、逻辑结构优化、情景创设优化和习题设计优化五个方面独具特色。因此该读本的推广以及开展的教学研究具有应用价值。
正如张景中院士所说:“把学数学比作吃核桃,数学教育研究的是如何砸核桃和吃核桃,而教育数学是研究改良核桃的品种,使核桃更美味、更营养、更容易砸开吃净。”教育数学思想的理论和应用需要我们不断探索和实践,希望我们都能把“改良核桃的品种”研究得更透彻,真正让数学变得容易。
