导管架式海上风机基础结构优化设计

2023-10-27王嘉其王宝来刘旭东

船舶 2023年5期

王嘉其王宝来刘旭东

（1. 烟台哈尔滨工程大学研究院烟台 264000；2. 中集海洋工程研究院有限公司烟台 264000）

0 引言

近年来，清洁能源的开发得到了世界各国的高度重视，其中风力发电技术更是发展迅速。随着我国风机建设规模不断扩大，发展方向也逐渐从陆地转向海洋。对于海上风机而言，基础结构成本占比通常在两成以上，且绝大部分在设计中存在明显的冗余，故可在保证结构安全的前提下降低建造成本，并更好地推动海上风电产业的发展。风机基础作为承受环境载荷和风机塔筒质量的关键结构，其建造工艺和材料尺寸影响着海上风机整体性能。通过对风机基础结构进行优化，能改善设计不足、提高结构性能，对结构选型和工程建设具有重要意义。

随着计算机性能高速发展，计算效率也大幅度提升。多种优化算法也相继提出，这些优化方法常选择对构件尺寸、基础布局和材料属性进行优化，以提高风机整体结构性能。潘祖兴等[1]提出了一种适用于海上风机基础过渡段的拓扑形式设计和优化方法，并对影响结构性能的拓扑参数进行优化，研究可应用于相似过渡段结构。CLAUSS等[2]利用形状的自动生成以及离散技术提出了一种形状的优化程序，通过非线性算法可以实现最小化目标函数的求解，研究同样可应用到不同类型的海洋工程结构中。GENTILS等[3]将参数化有限元分析与遗传算法相结合，提出了一种针对海上风机基础结构的优化方法，可同时对构件的外径和厚度进行优化。CHOU[4]采用拓扑方法对单桩基础平台进行了优化，计算了在风、浪联合作用下的平台承载能力，发现经优化后的结构动力响应显著降低。ALHAMAYDEH等[5]采用遗传算法对桁架构件进行优化，得到了在风、浪、地震载荷作用下构件最优末端节点位置和横截面积，证明了遗传算法在寻找最优解方面的优势。优化方法还可以找到结构设计冗余处，并通过改善构件设计提高风机经济效益。FENG等[6]在对导管架平台的形状优化设计中通过改变节点位置和横截面尺寸，实现了平台质量的最小化。MUSKULUS[7]选取遗传算法对风机底部圆锥形空心塔筒进行了形状优化，优化后的桁架式结构可节约大量钢材实现材料成本降低。SANDAL等[8]通过对导管架基础结构进行综合优化，确定了导管架的最佳桩腿距离，有效降低导管架基础结构的质量。优化方法在降低建造成本的同时还提高了结构性能。叶彦鹏等[9]对海上风机过渡段进行在减材设计中采用了拓扑优化，在极端环境荷载情况下结构应力明显降低，能有效避免应力集中。LEE等[10]对固定式海上风机的过渡段结构进行拓扑优化，优化后的结构质量更轻且热点应力更低，疲劳寿命显著提升。

虽然行业内对于海上结构优化研究已久，但针对海上风机基础结构研究较少，优化方法单一。本文以某四桩导管架式海上风机基础作为研究对象，采用试验设计（design of experiments, DOE）方法和粒子群算法的组合方法对结构进行合理的优化设计，寻找影响基础结构的主要构件参数，通过有限元分析方法对优化前后的模型强度进行比较，在保证结构安全的前提下，可实现对建造成本的有效控制。

1 环境载荷

1.1 风载荷

导管架式海上风机为三叶片风机形式，当风吹动风机叶片转动发电时，会产生3个方向上的力和转动力矩。载荷先传递到轮毂，再沿风机塔筒传递到过渡段基础，海上风机主要参数见表1。

表1 海上风机主要参数

该风机建设在水深较深海域，作业时海上风力较大，选用50年一遇的极端风况对风载荷模拟。自存工况下，轮毂处定常风速为37.5 m/s，选取Kaimal湍流模型模拟出600 s内175 m×200 m面积的湍流风场，如图1所示。可见风机自存工况下，风速呈现比较合理的正态分布，多稳定在30 ～50 m/s，鲜有60 m/s以上的强力风速。

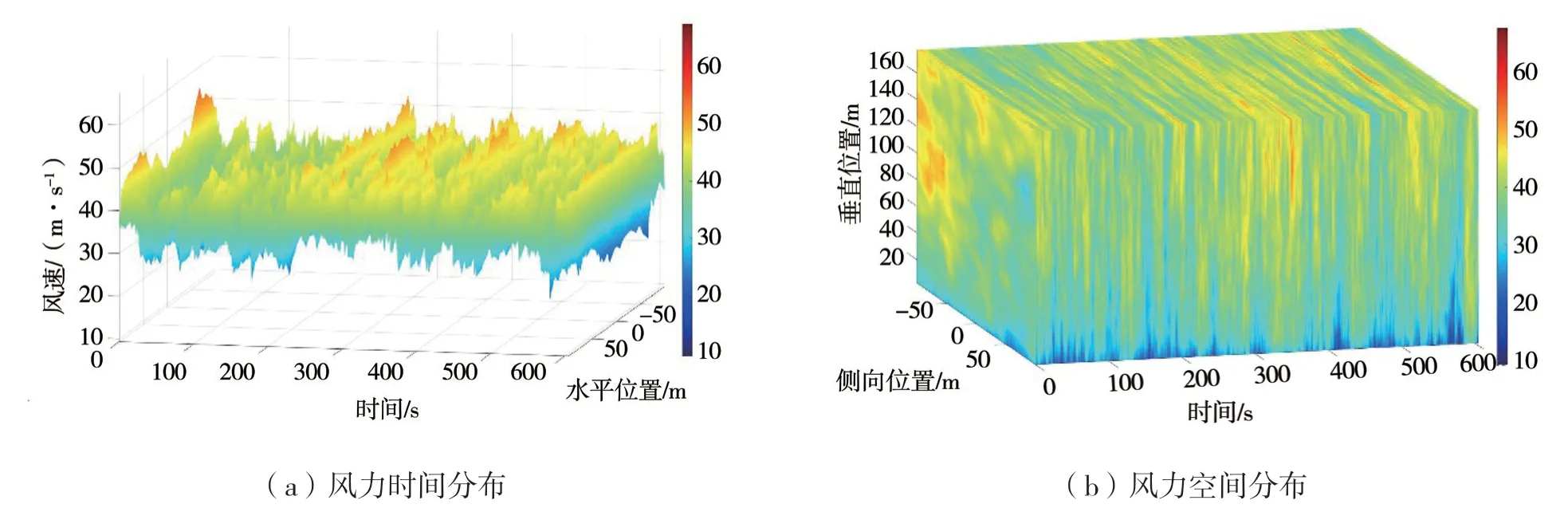
图1 自存工况三维湍流风场模拟图

以塔筒与过渡段连接处作为基准平面，在模拟的湍流风场作用下中心处3个方向上的力和转动力矩分别如图2所示。

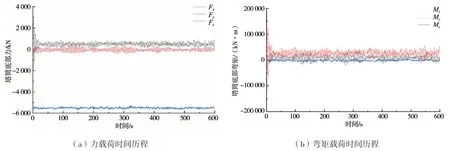
图2 自存工况6个分量载荷时间历程

可见：在0 ～ 20 s时，过渡段法兰处结构承力波动幅度剧烈，呈现逐步减小的趋势；而从20 s开始，过渡段结构承力趋于稳定，其中Z方向的载荷和X、Y方向的弯矩对结构影响较大。在1.5 s时基准平面处合力Fxy达到最大值，此时提取连接处结构所受6个分量载荷见表2，可以此进行风载荷作用下极端工况的静强度分析。

表2 作用在塔筒底端法兰处的极限载荷

1.2 波浪载荷

选取50年一遇的海况作为波浪条件，自存工况下有义波高为11.1 m。本文所研究的海上风机模型基础水线以下为导管架形式，桩腿会受到波浪载荷的影响。根据波浪理论选取Jonswap谱进行分析，将50年一遇自存工况下的海况条件进行时域分析600 s，波浪载荷合力如下页图3所示。可知，Z方向的浪载荷和X方向的浪弯矩对结构影响较大，而Y方向的浪载荷对结构几乎没有影响。该结果合理，可用于加载至海上风机进行静强度分析。

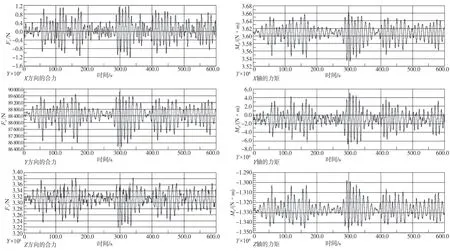
图3 自存工况波浪载荷合力的时间历程

2 海上风机基础结构静强度分析

2.1 海上风机基础有限元模型

导管架式海上风机基础结构主要包括2个部分，分别是最容易发生疲劳破坏的过渡段部分和起到支撑作用的导管架部分。其中风机基础过渡段主要由主钢管和四周的桩柱组成，主钢管和桩柱之间由盖板和腹板连接，纵向舱壁间采用带减轻孔的横向框架加固，由底板和封板将下部封闭，过渡段底板与桩柱之间通过肘板进行结构加强。风机基础过渡段结构参数见表3。

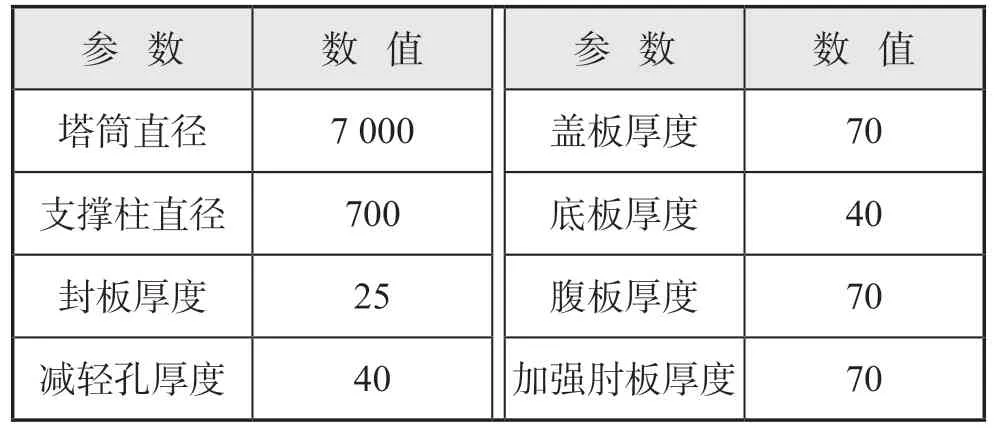
表3 风机基础过渡段结构参数 mm

由于过渡段结构主要由钢板构成，在建模过程中材料选取DH36钢材；同时为准确还原过渡段整体的形状，还采用了适应性很好的壳单元，主钢管与桩柱间采用平直连接形式。这种连接形式结构刚度更大、承受能力更强，更不容易被破坏。过渡段基础模型如图4所示。

图4 平箱梁式风机过渡段基础模型

导管架部分为四桩腿形式，由4根斜支撑和桩基管支撑整个海上风机，相连斜支撑之间由3对交叉支撑连接，斜支撑、交叉支撑小部分结构位于海平面以上，其余大部分结构位于海平面以下。桩基管则是插入海泥中，用于固定整个风机结构，其设计参数见下页表4。

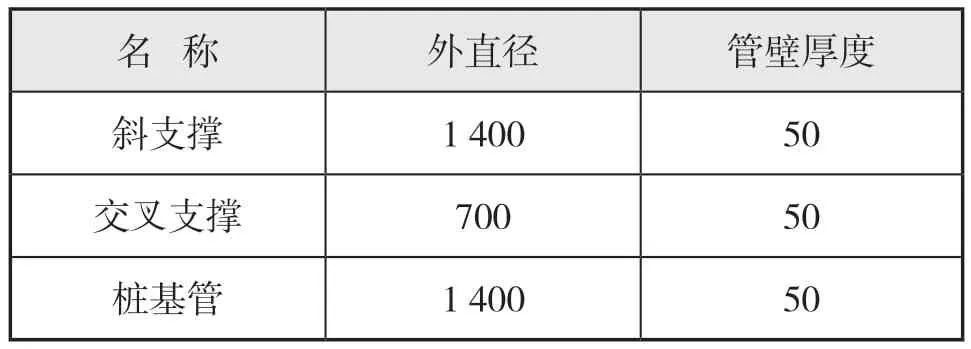
表4 导管架设计参数 mm

过渡段和导管架之间有1层X型甲板，其长、宽、厚度分别为15 m、15 m、0.04 m，模型的吃水深度为45 m，海平面距离甲板19.2 m。根据各设计参数可以建立海上风机基础结构的模型，如图5所示。选取6倍桩径法来处理桩土作用，甲板下的管单元与甲板壳单元通过耦合节点相连。

图5 导管架式海上风机基础结构

2.2 静强度分析结果

选用模拟得到的自存工况下的风、浪载荷进行加载，保持两者的入射方向一致。经过静强度分析之后，风机基础结构在极端风载荷和浪载荷共同作用下受到的最大平均应力和最大位移见表5。

表5 结构强度计算结果

为保证海上风机基础结构能够满足使用要求，在对风机基础进行强度校核时，许用应力应参照表6。其中，σs代表材料的屈服强度，为355 MPa。当需要校核极端条件下的应力时，可以在上面规定的基础上提高1/3。

表6 构件许用应力

通过与材料的许用应力比较，可见在风、浪载荷共同作用下，海上风机结构强度满足设计要求。绘制风机基础结构应力云图和位移云图，如图6所示。在风机基础结构中，应力最大位置位于桩柱与底板交接处附近，应力最小位置位于导管架桩基与斜支撑交接处附近；最大总位移位置则是位于过渡段顶部附近。

图6 风机基础结构云图

3 海上风机基础结构优化

3.1 优化设计流程

海上风机基础的静强度分析结果表明其结构设计存在安全冗余，因此在保证结构安全性的前提下可进行轻量化处理，有助于提高风机基础的经济性，降低建造成本，达到优化目的。采用DOE方法和粒子群算法集成的优化方法，对极端风载荷、浪载荷共同作用的最危险工况进行结构优化设计，分析各个部件尺寸对结构性能的贡献率，寻求最优尺寸组合。优化设计的整个流程如图7所示。

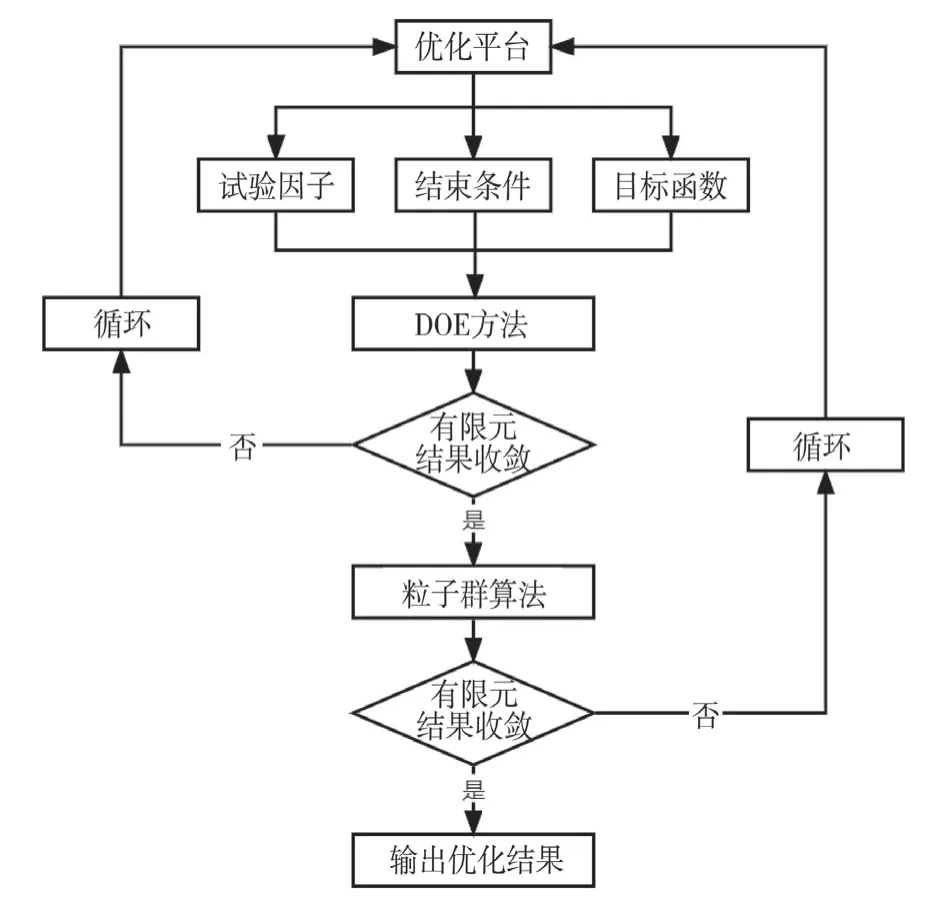
图7 DOE方法和粒子群集法的集成优化设计流程

试验选取主钢管厚度、肘板加强厚度、盖板厚度等13个因子，初始尺寸具体见表7。

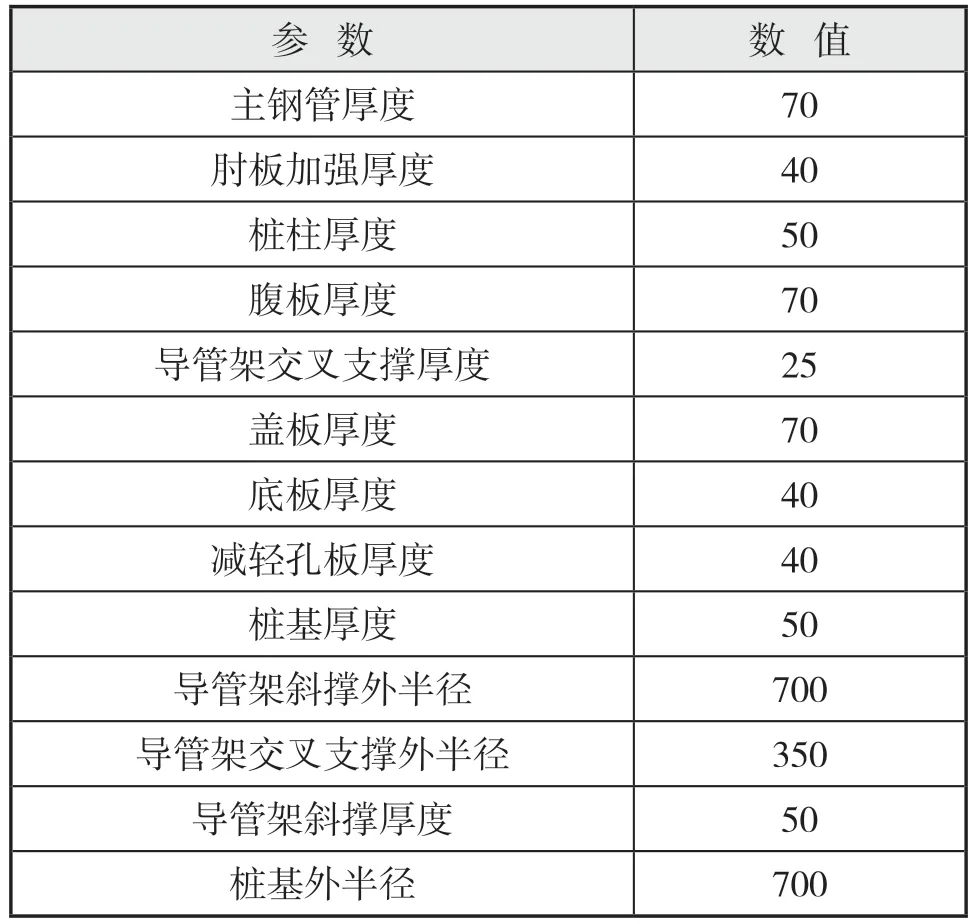
表7 因子初始尺寸 mm

约束条件选取海上风机基础结构的强度，并以最大应力准则为结构的破坏准则，设置最大应力上限为材料的屈服强度。目标函数为目标输出参数，选取结构最大平均应力、最大位移，以及整体质量的目标设置为最小值。

3.2 优化设计结果

3.2.1 DOE结果

在DOE中，选取最优拉丁超立方设计方法对平箱梁式海上风机基础模型进行试验设计分析，设置设计矩阵的个数为500个，13个试验因子的取值范围为初始值的±50%，最大平均应力、最大位移和整体质量这三者的权重系数都为1.0。经过500次的试验设计分析后，通过可行性设计点历史图即可观察到DOE中各设计因子和目标响应的历史输出，能够显示每次试验后所得优化结果的变化情况，如下页图8所示。其中黑色圆点代表符合条件的点，蓝色圆点代表符合要求的点，绿色圆点则代表最佳设计点。

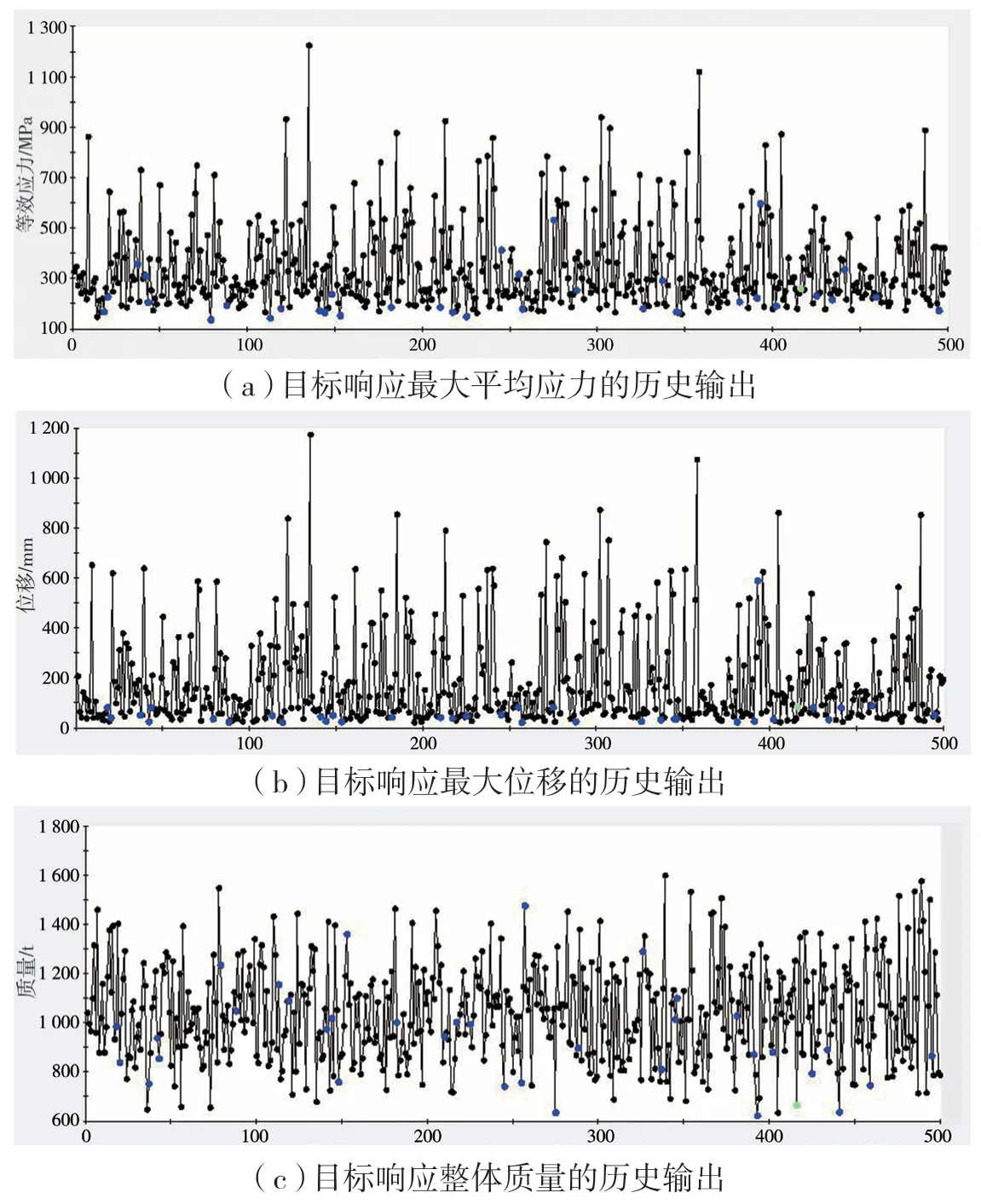
图8 DOE可行性设计点历史图

由图8可知，在响应的历史输出中，其走向趋于1条直线，波动幅度较小且大部分的设计组合都符合目标响应的要求，表明通过优化的拉丁超立方设计方法生成的设计矩阵多数是成熟有效的，且设计因子的取值范围也合理。在前500次试验设计组合中，第416组参数被鉴定为最佳解。在该参数组合条件下以及因子的取值范围内，达到了结构整体最大平均应力、最大位移以及整体质量的综合最小化。此时，最大平均应力为260.832 MPa，最大位移为85.856 3 mm，整体质量为665.397 8 t。

13个设计因子对最大平均应力、最大位移和整体质量的主效应如下页图9所示。

图9 各设计因子对目标响应的主效应

从图9可见:桩基的外半径对于最大平均应力影响最大，桩基的厚度、斜支撑的外半径对于最大平均应力影响较大。随着桩基外半径的增加，平均应力指标呈现出先逐渐减小后逐渐增大的曲线走势，其他设计因子则影响较小且基本呈线性关系。同时可以看出，桩基的外半径和厚度对于最大位移影响都较大。最大位移指标随着桩基外半径的增大呈现出先减小后上升的趋势，其他因子同样也是基本呈线性关系。斜支撑外半径对于平均应力影响最大，平均应力随着斜支撑外半径的增大而线性增大，并且所有因子都呈线性关系。

13个设计因子对最大平均应力、最大位移和整体质量的贡献率如下页图10所示。

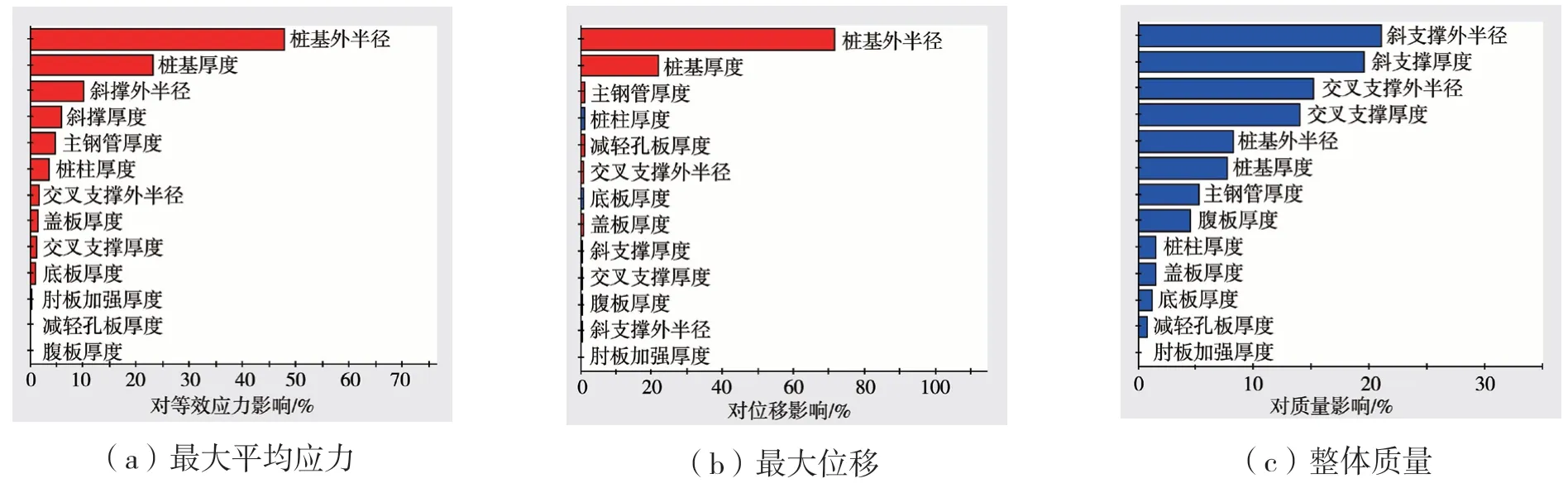
图10 各设计因子对目标响应的贡献率图

桩基外半径和厚度对于最大平均应力贡献率较大（分别为-47.711%和-22.972%），腹板厚度对于最大平均应力贡献率最小（为-0.074%），所有因子对于最大平均应力都是负的贡献。桩基外半径和厚度同样对于最大位移贡献率较大（分别为-71.497%和-21.737%），且波动幅度远大于其他设计因子，肘板加强厚度对于最大位移贡献率最小（为-0.112%），均为负的贡献。斜支撑外半径和厚度对于整体质量的贡献率较大（分别为20.998%和19.519%），都为正的贡献；肘板加强对于整体质量的贡献率最小（为-0.015%），为负的贡献。

3.2.2 多目标算法优化设计结果

根据DOE结果，选取第416次试验设计的参数组合作为后续多目标算法优化的初始尺寸，同时为了减少工作量，提高计算效率，选取在DOE分析中综合贡献率最大的4个设计因子作为多目标算法优化设计的设计变量。采用粒子群算法对海上风机基础模型进一步试验设计分析，其中：最大迭代次数为50次、粒子数为10个、总共需要进行500次分析，取值范围设置为初始值的±50%，设置约束条件，目标响应同样为最大平均应力、最大位移和整体质量最小化，进行更精准的优化分析。经过500次的分析后，参数优化结果如图11所示。图中黑色圆点代表符合条件的点，蓝色圆点代表符合要求的点，绿色圆点则代表最佳设计点，而红色圆点代表不符合要求的个体。可见，尽量有一些设计组合不满足约束要求，大部分都满足要求，结构的最大应力和最大位移都在往减小的方向不断收敛。

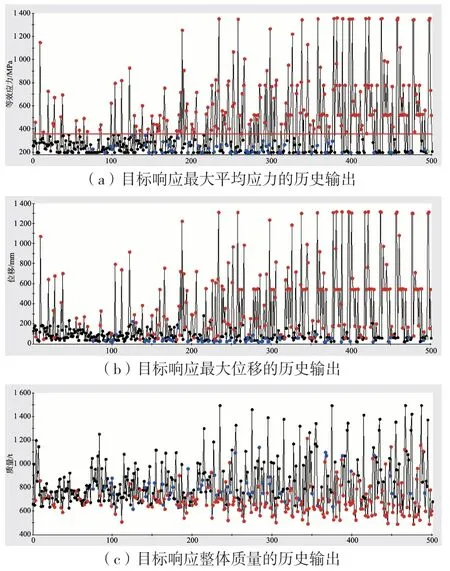
图11 粒子群算法可行性设计点历史图

通过优化计算所得的可行解，构成了该多目标全局优化设计问题的帕累托解集，如图12所示。

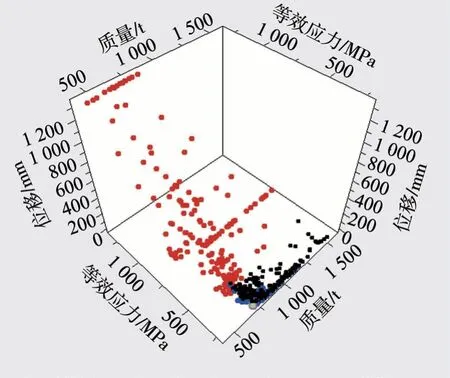
图12 帕累托解集及前沿

在所有个体中存在着许多不可行解，不符合要求的个体用红色圆点表示，符合要求的个体用黑色圆点表示，而蓝色圆点和绿色圆点分别表示可行解。由相互连接的蓝色圆点和绿色圆点组成的线条被称为帕累托前沿。在可行解中存在粒子群算法推荐的最佳解，即为图中唯一高光的绿点所表示的个体。

选取粒子群算法推荐的绿色可行解作为本文优化设计的最佳解，对应的尺寸参数组合也被确定为最佳尺寸标准。在进行了500次的算法优化后，第496次得到的绿色可行解被确认为是最佳解。

通过静力分析对最佳解的可行性进行验证，在验证可行性之前，为了提高有限元分析软件的计算效率，将优化分析得到的最佳参数尺寸取整，如表8所示。

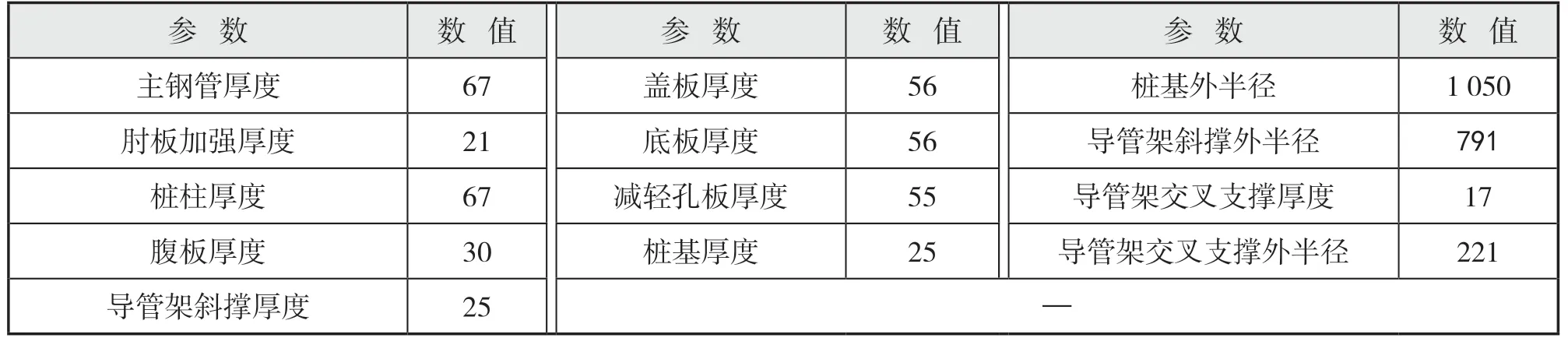
表8 最佳参数尺寸 mm

将最优参数组合尺寸数值取整后，输入至有限元分析软件属性编辑模块中，对最优参数组合模型进行计算分析和校核。最优参数组合模型结构所对应的应力云图和位移云图如图13所示。

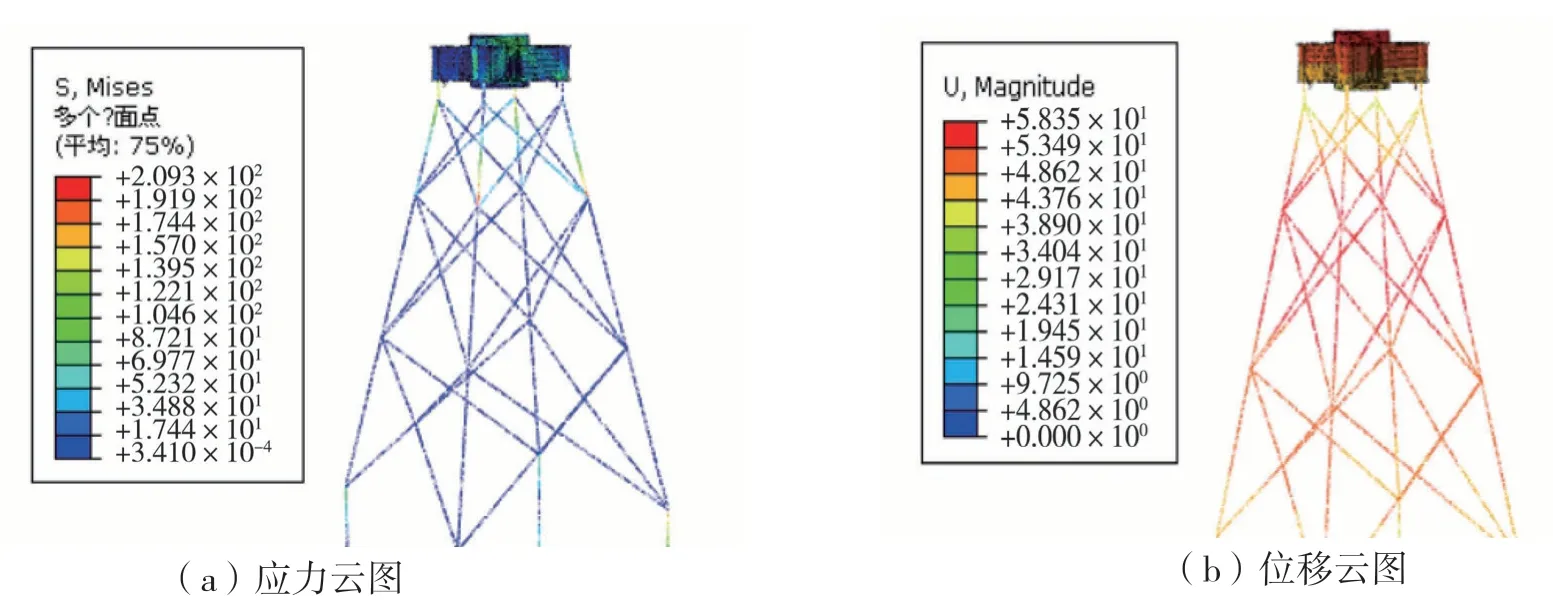
图13 优化后模型的应力和位移云图

优化前后的结构应力、位移和质量对比见下页表9。优化后的平箱梁式海上风机基础结构与初始模型相比，最大平均应力增加了11.5 MPa，最大位移增加17.25 mm，增幅均较小，满足设计要求，而整个海上风机基础结构的质量减轻133.659 t，轻量化效果显著。应力极值位置出现在导管架上半部分交叉支撑与斜支撑交界处附近，与初始模型应力极值位置相比有所不同；优化后的模型位移极值位置位于导管架上半部分的斜撑附近，与初始模型位移极值位置区别不大。综上所述，DOE组合粒子群优化算法方法合适且稳健，能在满足强度设计要求的条件下有效减轻结构质量，实现轻量化优化设计。