基于CFD的风电安装船首部砰击载荷分析

叶 晗 黄亚南 李飞虎 冯 珺 康 琪

（大连海洋大学 航海与船舶工程学院 大连 116023）

0 引 言

在全球可再生能源产业日益增长的背景下[1]，风能因其巨大的环境效益和商业潜力而获得快速发展。为实现2050年零排放的目标[2]，有必要进一步发展风能，特别是海上风能。为此，各国加快了海上风电项目的建设。由于深远海域风能资源更加丰富，因此走向深远海是海上风电项目的未来趋势。然而，海上风电场的基础、建设和安装成本占开发成本的比例较高，比陆地上的相应成本高出近3.6倍。鉴于海上风电场所处的风况、海况和海床的具体特点，水波和风压将极大地影响风电场开发的安全性和经济性。艏部位置是风电安装船重要受力处，因此研究艏部砰击载荷尤为重要。

波浪砰击是船舶海洋工程领域的一个重要问题，也是造成船体结构破坏的主要原因之一。自20世纪60年代初以来，国内外学者相继开展大量砰击研究，包括理论研究、试验研究和计算仿真研究等。近些年来，有关砰击问题的理论研究主要集中于船体局部垂直入水砰击（即二维砰击理论），该研究相对简单且更为成熟。COINTE[3]研究了二维情况下水波冲击刚性结构物的问题，采用一种基于波浪冲击力的分析方法，通过计算分析得出了波浪砰击的时间历程、瞬时冲击力的分布和砰击面积等参数；同时，该研究还讨论了波浪砰击对结构物稳定性和疲劳寿命的影响，并提出了相应的建议和措施。HOWISON等[4]研究了小入水角度情况下，不可压结构物的入水问题，并进行了数学建模和理论分析。研究发现，入水问题涉及到很多物理现象（如空气被夹带进入水中，水面的形变和扰动等），论文提出了一种基于边界元方法的数值计算模型，可以较为准确地描述这些物理现象的发生和演化过程，通过计算分析便可得出不同入水角下的入水形态、水下压力分布等参数。

研究船舶波浪砰击问题的最终目的是为了在实际工程中应用。陈占阳等[5]研究了外张砰击载荷的时间分布规律，其通过模型试验，采用高速压力传感器测量砰击载荷的时间历程，并进行分析和拟合，得到了外张砰击载荷时间分布的数学模型。洪尧等[6]对圆盘入水砰击载荷进行试验研究，在不同入射速度和角度下，对入水的砰击载荷进行测试和分析，研究结果表明入射速度和角度都对砰击载荷有显著影响，会产生剧烈的波浪和喷溅现象。

随着科技的飞速发展，海上工程越发普遍，也引发更多实际问题。传统的理论方法已经难以解决各种实际问题，其局限性变得越来越严重。而实体试验研究不仅需要耗费大量时间和成本，还存在很多不可抗因素，使得人们开始将目光转向数值仿真计算，以解决砰击问题。

司海龙等[7]结合计算流体力学（computational fluid dynamics, CFD）数值模拟计算技术和船舶的时域运动预测方法，得出可适用于一般船型的砰击载荷预测方法。研究表明，砰击载荷系数的大小，与船舶入水速度、浪向角以及船舶首部在波峰、波谷位置都有非常大的关系。刘正国等[8]为了计算某江海直达船整船在波浪中的运动，使用AQWA软件分析得到船体表面三维形状和船舶航行速度对船舶所受砰击载荷的影响，并提出可行性优化方案。吴小平等[9]利用Nastran软件，基于频域法对船舶尾部与首部偏大的客滚船进行计算模拟，将砰击载荷反应到有限元计算模型的各部分上，得到客滚船砰击强度的安全评估报告。张文挺等[10]对计算船舶的运动响应进行研究，基于时域非线性方法并结合三维Rankine源法，得到了船舶的垂向相对运动速度，进而结合砰击力系数计算出船舶的砰击载荷。

本文基于CFD并使用STAR-CCM+商业软件与重叠网格技术，结合六自由度刚体运动模型，自由液面捕捉采用流体体积（volume of fluid,VOF）方法，在规则波（斯托克斯五阶波）作用下，对不同波高和波长下的风电安装船首部砰击载荷进行计算。

1 CFD理论基础

1.1 控制方程

基于雷诺平均N-S方程，考虑流体不可压缩，连续性方程和雷诺平均N-S方程如下：

式中：iμ为时均速度，m/s；ρ为流体密度，kg/m3；t为时间，s；ν为流体的运动黏度，mPa·s；fi为质量力，N；P为流体压强，Pa；μ'i为脉动速度，为雷诺应力项。自由液面捕捉采用VOF方法。

1.2 k-ε湍流模型

本文选用标准k-ε模型，其稳定性较好并且计算精度高，湍流黏度方程表示为：

式中：Cμ代表经验常数，取值为0.09。

k和ε对应运算方程如下所示：

式中：C1ε、C2ε、σk、σε分别取值1.44、1.92、1.0、1.3；Gk为湍动能产生项，表达式如下：

1.3 造波方法

本文采用斯托克斯五阶波，其中包含了多个非线性项和耗散项。斯托克斯五阶波的方程如式（7）至式（10）所示。

波浪剖面方程η：

水平速度u：

垂直速度v：

速度势φ：

式中：波长为L，m；波浪周期为T，s；波数为k；波速为c，m/s；波形系数为nφ；速度势系数为nη。

2 船型参数与工况选取

2.1 几何模型与边界条件

目标船型吃水较浅、甲板面积大，可存放数量较多的风机设备。船上配备1台主起重机、2台辅吊机以及船首定位装置，可在最大作业水深为40 m的近海进行作业。风电安装船主尺度如表1所示，全船表面模型如下页图1所示，同时在船首位置布置了16个观测点，参见下页图2。

图1 风电安装船模型

图2 船首观测点

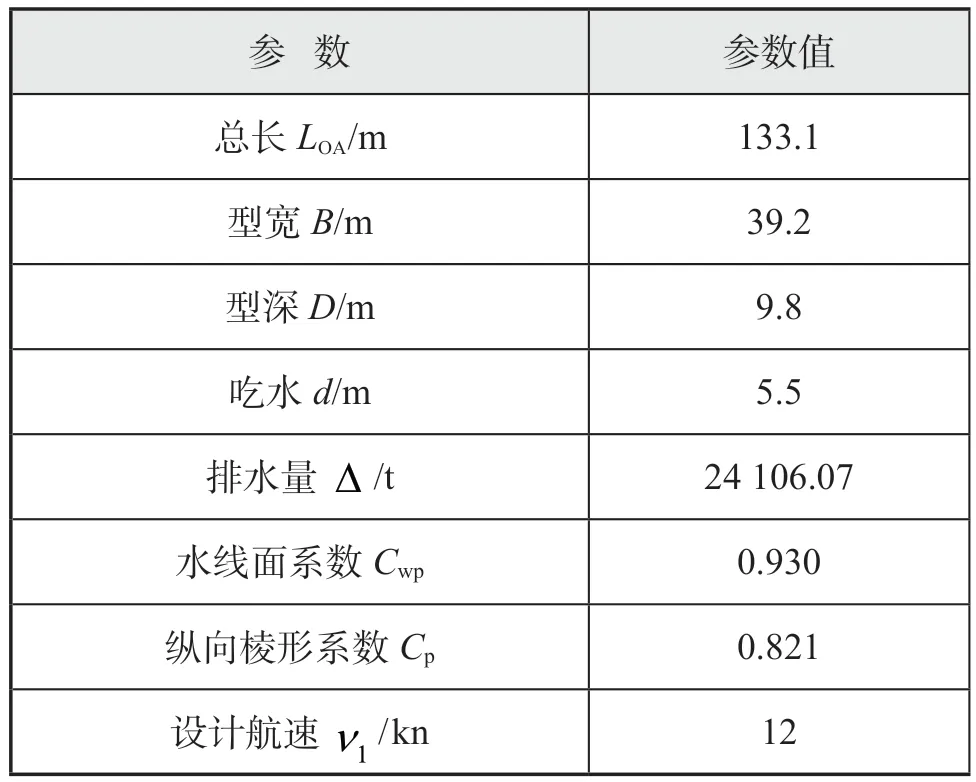
表1 风电安装船主尺度

由于设置船舶为迎浪，船横摇角度较小，并且流场具有对称性，所以采用半船计算域。计算域中船首方向为速度入口，船尾方向为压力出口，船首距离速度入口为1倍船长，船尾为2倍船长，如图3所示，为了防止出口处波浪反射对流场造成影响，在出口处激活阻尼消波。

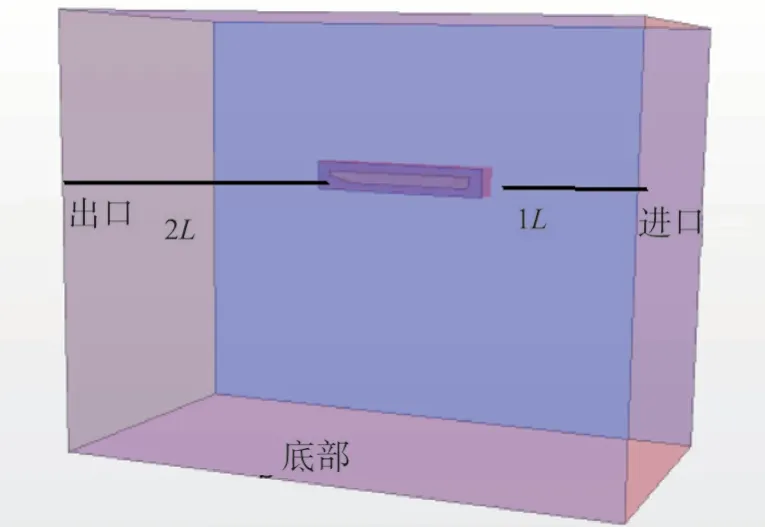
图3 计算域及边界条件

2.2 工况选取

为了探究船首处波浪载荷与波浪参数的规律，根据风电安装船工作特性设置船舶为迎浪运动，船体满载吃水5.5 m。本文设计了3组不同波高，分别为2 m、3 m、4 m；5组不同波长，分别为66.5 m（0.5倍船长）、106.4 m（0.8倍船长）、133.0 m（1倍船长）、159.6 m（1.2倍船长）、266.0 m（2倍船长）。共计15组计算工况，如表2所示。

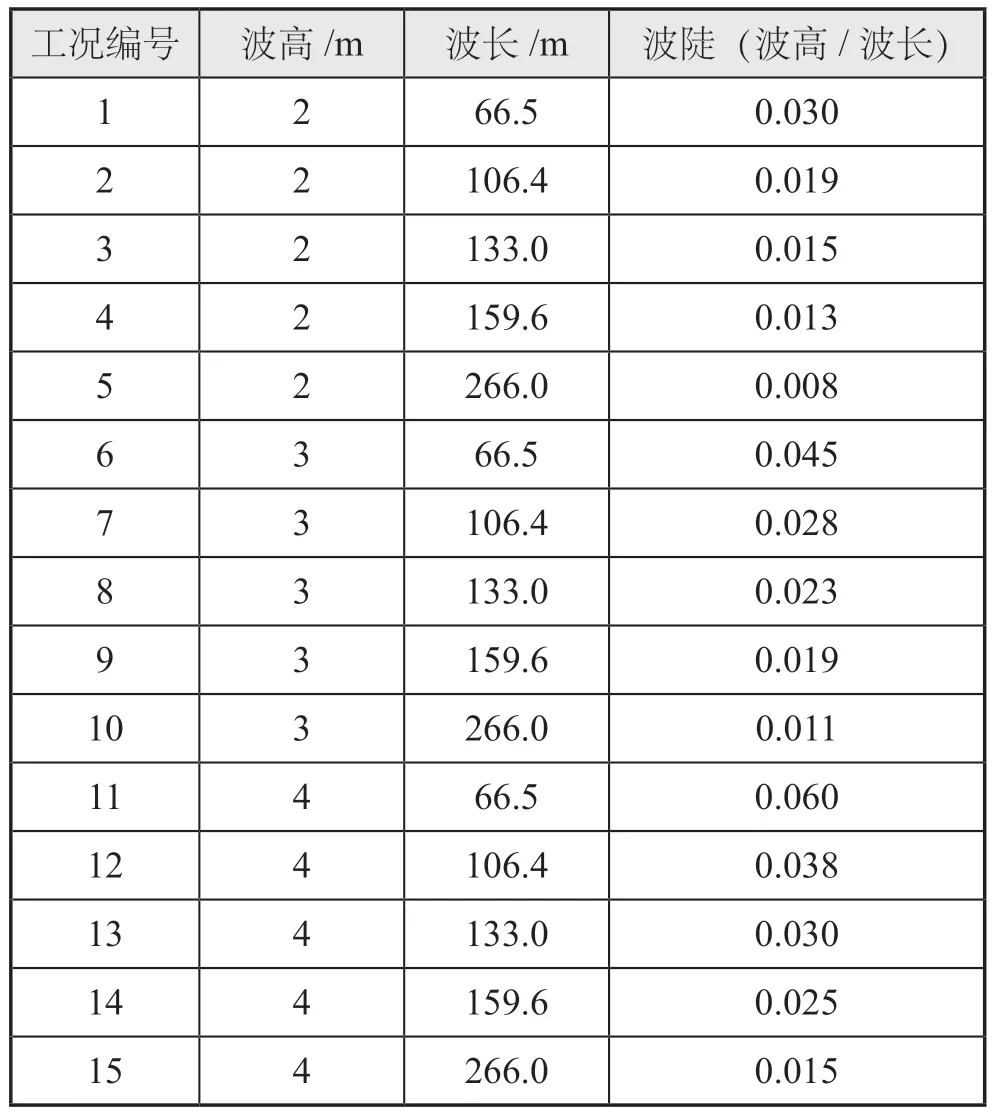
表2 各组工况参数

为了计算分析便利，本文采用模型缩尺比1∶20，三维数值水池中对应各波高分别为0.10 m、0.15 m和0.20 m，波长分别为3.325 m、5.320 m、6.650 m、7.980 m和13.300 m。

3 网格划分与数值方法验证

本文采用VOF方法进行自由液面捕捉，将计算区域分为若干个小单元，每个小单元内的流体状态用1个分数来描述，表示该单元内流体的体积分数。通过对这些小单元体积分数的计算，可以得到流体的总体积和质量。本文为更好模拟波浪运动的变化，划分数值水池网格时，在自由液面上下一个波峰处进行了网格细化，而其余网格则采用线性递增的方式进行划分，以节省计算资源。这种网格划分方法可以更好地捕捉自由液面变化，提高模拟准确度。自由液面处的网格划分方案如图4所示。

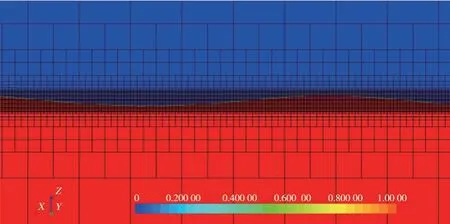
图4 水和空气体积分数示意图

为验证数值方法的稳定性，采用速度入口边界造波，且对自由液面处划分不同尺度的网格，讨论网格密度对造波产生的影响。基于安装船模型，选定1个计算工况（波高0.2 m、波长6.65 m），在波浪场中，X轴方向上，由原点向正负方向等距离（4 m）选取观测点，如图5所示。

图5 波浪场示意图

随着波浪衰弱进行，离速度入口越远、衰弱越明显，所以着重观测速度入口远端点（-8观测点）。计算时间步长取0.01 s，1个波高方向网格取10 ～30个进行比较。

当时间步为0.01 s时，1个波高方向网格设置为10、20和30个，并进行加密；网格高分别为0.020 m、0.010 m、0.007 m，且自由液面处单个网格的横向间距x与垂向间距z的比例一般选取为1∶2、1∶4或者1∶8。具体比例可根据波陡参数进行选取，本文选取x/z=1∶4，横向网格密度与纵向保持一致。数值水池网格具体划分形式如表3所示。

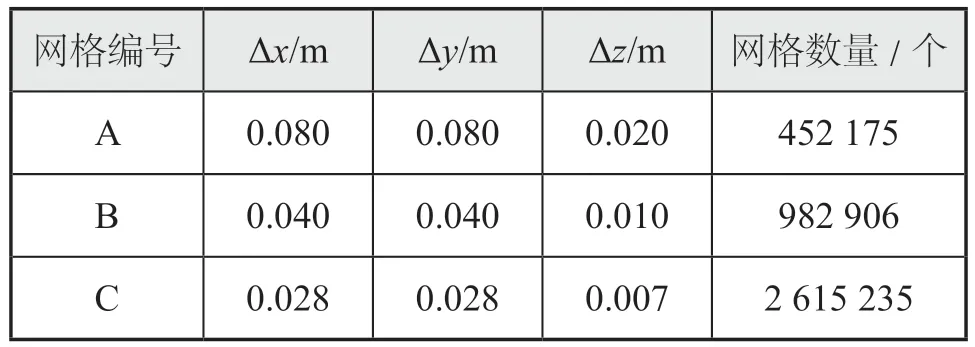
表3 数值水池网格划分方案

将不同网格划分下的观测点距原点时历曲线与理论值相比较（如图6所示），可发现在计算时间内：当网格为10个时，波浪衰弱较明显；当网格为20个和30个时，波浪衰弱都不明显，符合计算要求。综合计算时间成本考虑，当网格大于20个再增加时，计算结果基本无明显变化，因此选用网格为20个、网格高为0.01 m，作为本文计算网格划分方案。

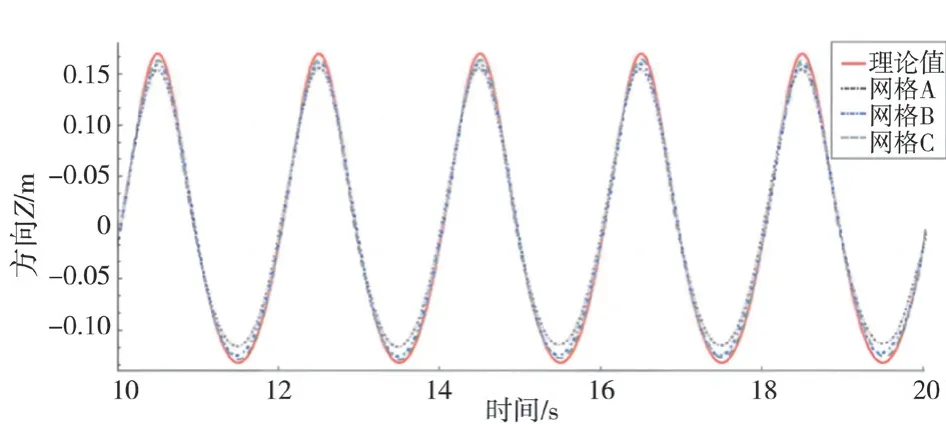
图6 不同网格高度下，观测点距自由液面高度

4 数值计算结果及分析

本文通过边界造波方法，实现了斯托克斯五阶波的数值模拟，该方法以不可压缩黏性流体的N-S方程和VOF自由液面捕捉法为基础，借助Star-CCM+软件定义了入射边界处波浪解析表达式，从而模拟了五阶斯托克斯波的产生与传播。

风电安装船在波浪中航行，定义其设计航速为12.0 kn。缩尺比1∶20下，设计航速为0.6 kn，同时波高分别为0.10 m、0.15 m和0.20 m，波长分别为3.325 m、5.320 m、6.650 m、7.980 m和13.300 m。如图2所示，共取16个观测点。当波高为0. 15 m、波长为6.65 m时，比较观测点1、5、9、13（x不同，z相同）；点2、6、10、14（x不同，z相同）；点3、7、11、15（x不同，z相同）；点4、8、12、16（x不同，z相同）。这4组受力情况见图7至图10，图11为船体压强云图。

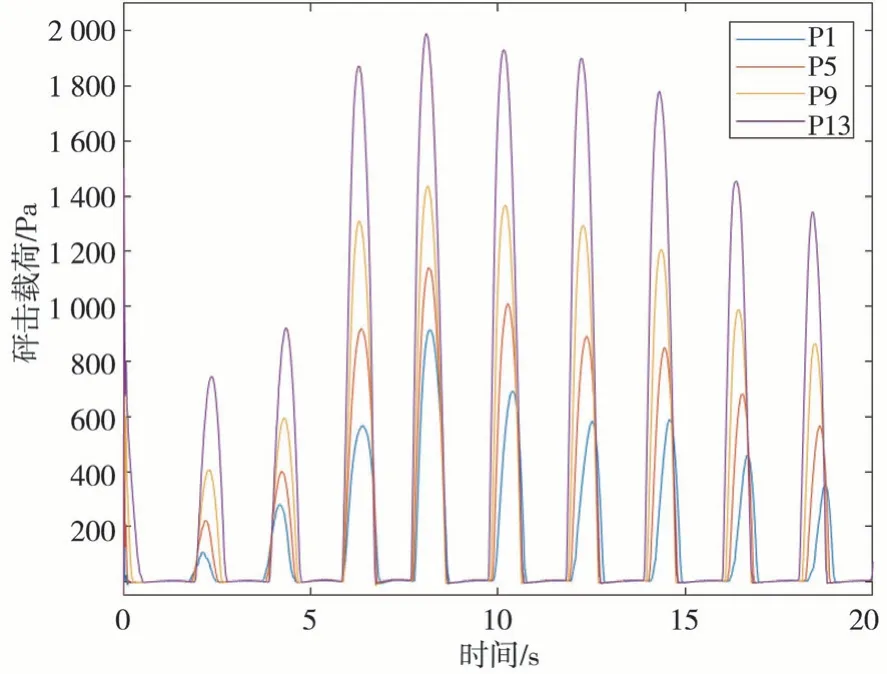
图7 观测点1、5、9、13砰击载荷对比曲线

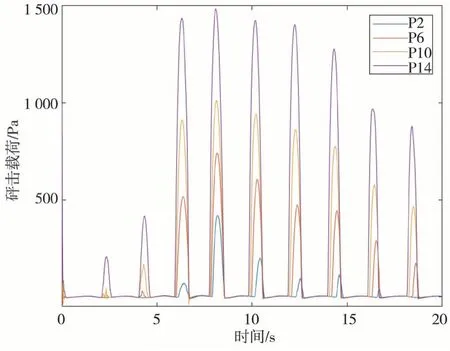
图8 观测点2、6、10、14砰击载荷对比曲线

图9 观测点3、7、11、15砰击载荷对比曲线

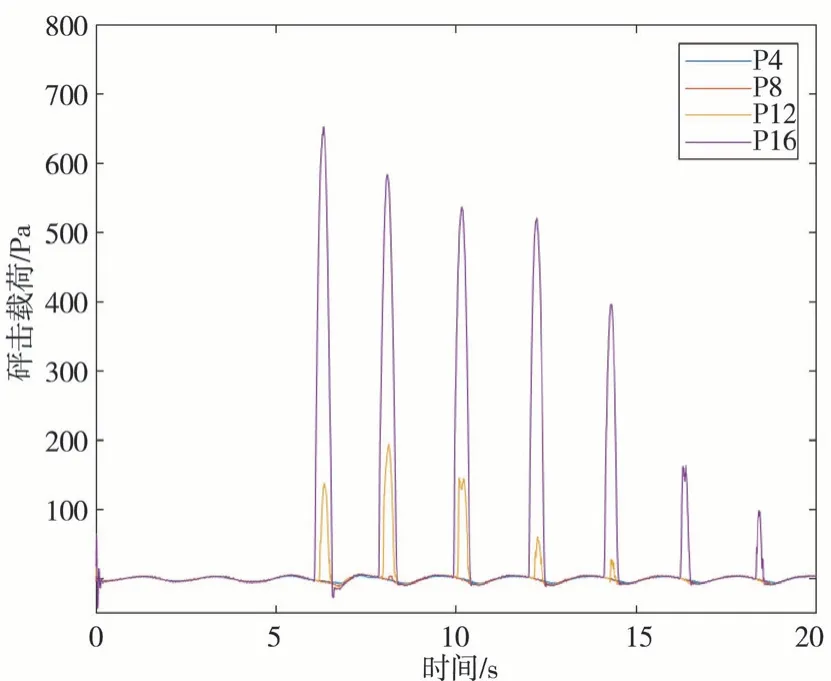
图10 观测点4、8、12、16砰击载荷对比曲线

图11 船体压强云图

可见，此4组总体受压情况为离水线越近，所受砰击载荷变化越大。本文重点研究砰击载荷的变化，所以重点分析距水线较近的1组，参见图7。

由此可知，离船首越近时砰击载荷越大，砰击载荷曲线变化剧烈，短时间内即可到达极值。此种砰击会导致船舶加速度出现突变，对船舶结构破坏较大；同时也发现，高度相同时，砰击载荷的周期几乎相同。

当波高为0.15 m、波长为6.65 m时，比较观测点1、2、3、4（x相同，z不同）；点5、6、7、8（x相同，z不同）；点9、10、11、12（x相同，z不同）；点13、14、15、16（x相同，z不同）。这4组的受力情况，见图12至图15。

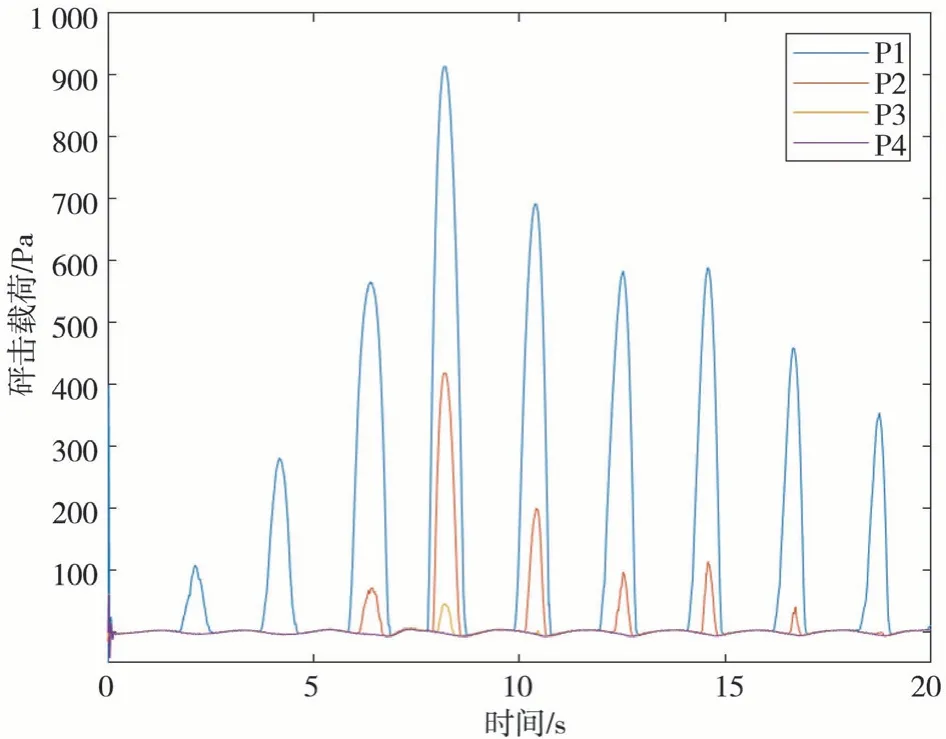
图12 观测点1、2、3、4砰击载荷对比曲线

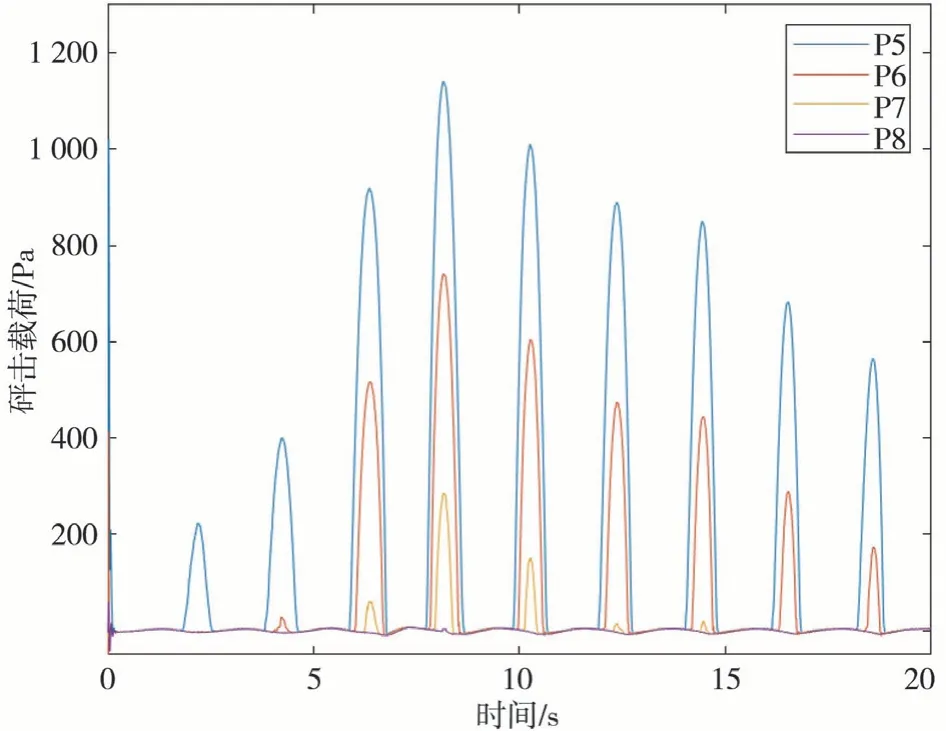
图13 观测点5、6、7、8砰击载荷对比曲线

图14 观测点9、10、11、12砰击载荷对比曲线

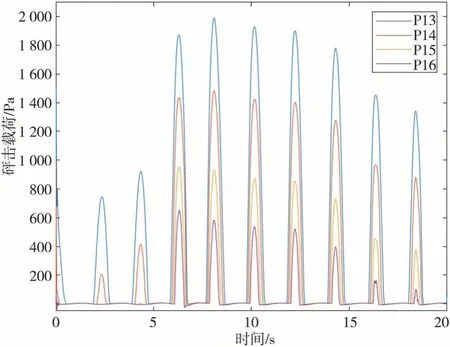
图15 观测点13、14、15、16砰击载荷对比曲线

由此可知：离水线面越远，砰击载荷越小，距水线面较远的2组观测点，由于几乎没接触水面，所以砰击载荷较小，因此重点比较离水线较近的观测点。

通过上述比较发现，船首最前端靠近水线面处的砰击载荷为最大值。为了探究成因，通过比较船模纵摇和砰击载荷曲线发现，船模垂荡周期与砰击载荷周期相同。如图16所示，由此可以推断，船首砰击载荷产生的主要原因是船首的出水与入水所造成；波浪冲击船首外飘区造成的外飘砰击较小，可能是由于外飘面积大且作用时间长。由于点13处的砰击载荷为最大值，所以下文将主要对点13处的砰击载荷规律展开研究。

图16 船模纵摇和砰击载荷曲线

当波高为0.15 m时，比较不同波长下（波浪周期），点13处所受的砰击载荷，如图17所示。当波长等于船长时，所受砰击载荷最大。由船舶耐波性可知，在规则波中，当L/λ在1附近时，波浪的扰动力最大，纵摇和垂荡都十分剧烈。由此又证明了船首的波浪载荷主要是由于船舶在波浪中出水、入水所导致。

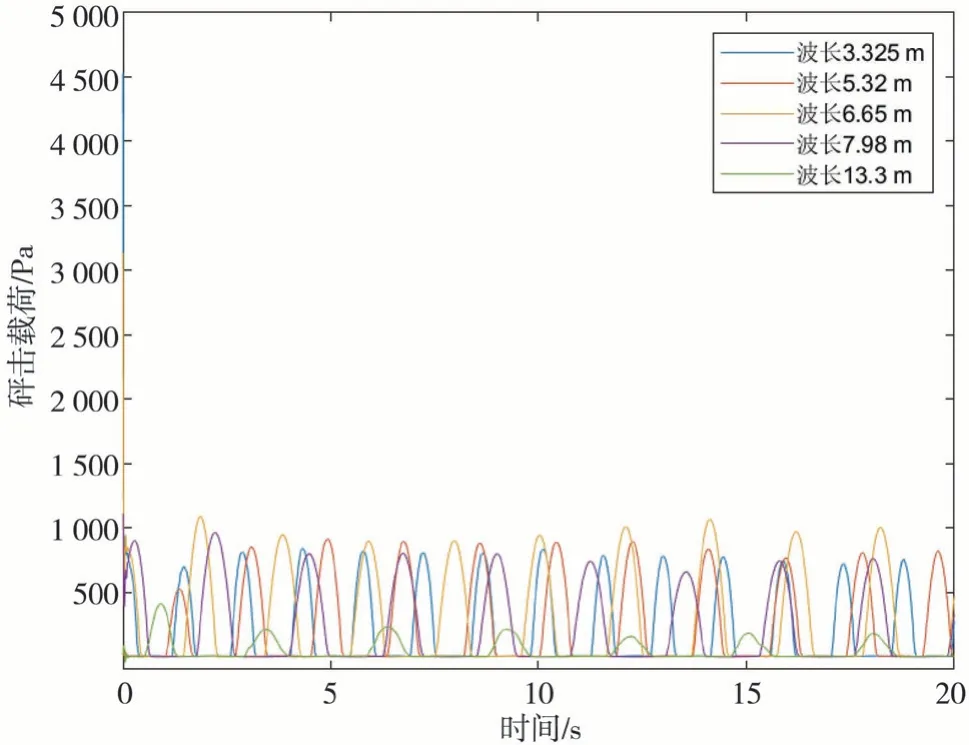
图17 观测点13在不同波长下的砰击载荷时历曲线

由以上结论可以判断出，当波长等于船长时，船首靠近水线面处所受砰击压力最大。由此对波长等于6.65 m时，点13处在不同波高的砰击载荷进行研究，参见下页图18。

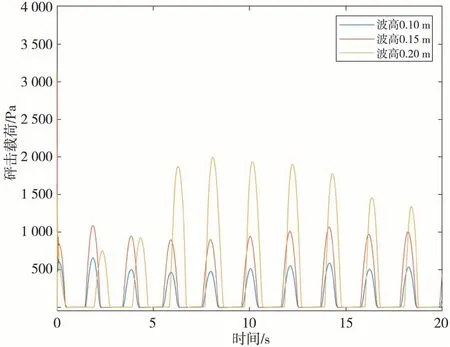
图18 观测点13在不同波高下的砰击载荷时历曲线

由此可见，当波高为0.2 m时，点13处所受砰击载荷最大。

5 结 语

综上所述，风电安装船作业中：随着波高增大，船舶首部砰击载荷越大；随着波长增长，砰击载荷呈先上升后下降的趋势；当波长等于船长时，砰击载荷达到最大值。船首砰击主要由船舶在波浪中出水、入水所导致，其剧烈程度与船舶纵摇幅值相关，减少砰击载荷就是减少纵摇幅值，因此船舶应当加强首部结构强度。并且，因距水线面越近的点所受砰击压力越大，所以风电安装船首部距水线面较近位置的结构强度尤其需要重点加强。

本文分析了船首位置砰击载荷分布以及载荷峰值最大值，为风电安装船首部强度设计提供了参考。