花瓣形棒束通道内单气泡上升行为数值模拟研究
2023-10-27张文超李嘉元孙建闯金光远蔡伟华
张文超,李嘉元,杨 光,孙建闯,金光远,蔡伟华,*
(1.东北电力大学 热流科学与核工程实验室,吉林省 吉林市 132012;2.清华大学 先进反应堆工程与安全教育部重点实验室,北京 100084)
核能广泛应用于发电、制氢、区域供热和海水淡化等领域,在双碳目标下,要实现能源供应向清洁、低碳转型,核能必不可少[1]。开发高性能新型燃料棒可有效改善反应堆热工水力性能。花瓣形燃料元件最早应用在俄罗斯破冰船用反应堆中,燃料棒横截面呈花瓣形状。根据美国Lightbridge公司的推荐[2]分别将燃料棒包壳及芯块设置为Zr-4合金与铀、锆质量分数为50%的合金(U-Zr Alloy),与传统的燃料元件相比,花瓣形燃料棒具有表面积-体积比大、促进子通道混合、不需要定位格架等优点,已有研究表明[3],采用金属螺旋十字形燃料元件,在保持或提高安全裕度的同时,可以显著提高当前压水堆的功率(约20%),因此,花瓣形燃料元件在小型反应堆中具有较为广阔的应用价值[4]。花瓣形燃料棒具有螺旋结构,因此,与传统圆形燃料棒组件相比,组件内冷却剂流动具有独特的热工水力特性。目前,美国、俄罗斯等世界核工业强国已经在花瓣形燃料棒上开展了相关工作,取得了一定的研究成果。我国仅对热工水力特性开展了初步研究,对气泡行为、临界热流密度等热工水力基础问题认识不深。
燃料元件周围的气泡会影响流道内的热工水力特性,通道内的流道规律十分复杂[5],因此有必要研究通道内的气泡行为。张明昊等[6]采用MPS-MAFL方法针对静止条件以及入口流量脉动条件下的单气泡垂直上升运动行为进行了分析。结果表明,脉动条件下,气泡形状和上升速度的波动周期均与流量周期相同,且波动幅度随流量脉动幅值的增大而增大。孙姣等[7]进行了静水中气泡在竖直壁面附近上升运动实验研究,发现在壁面附近气泡呈二维“之”字形周期性振荡上升。Li等[8]进行了气泡在水中上升运动的三维数值模拟,用流体体积法(VOF)捕捉气泡界面。结果表明,在旋流流场中,气泡向中心迁移,迁移运动受剪切力、气泡尺寸和涡流强度的影响。Basit等[9]研究了摇摆条件下静止液体中单个气泡的上升行为,分析了在摇摆条件下液体黏度和气泡尺寸等因素对气泡运动轨迹和上升速度的影响。
在气泡形状研究方面,将气泡形状参数与Grace气泡相图[10]对比是确定气泡形状准确性的一个重要手段。Wang等[11]进行了液态铅铋合金中气泡上升行为的数值模拟,基于漫反射界面法得到了气泡的形状变化。结果表明,气泡初始尺寸越大,其变形程度越大,同时气泡越容易发生分裂。Gu等[12]进行了水平和倾斜通道内气泡运动的实验研究,发现气泡上部和主体的形状取决于弗劳德数,而气泡背面的形状取决于弗劳德数和气泡尺寸。Kazuya等[13]模拟了二维气泡的上升,得到了单个气泡的上升速度和压力变化,并研究了不同尺寸气泡的形状变化差异。
花瓣形螺旋棒具有体表比大和自螺旋两大特点,从而可实现强化换热[4],因此可作为换热器强化换热管和核反应堆燃料棒等。与常规圆形棒束通道相比,花瓣形棒束通道内有明显的二次流[14],其独特的流场特性会导致气泡行为发生显著改变。目前,已有研究主要集中在二维气泡行为数值模拟以及单流道内的气泡运动实验上,而花瓣形棒束通道内三维气泡的行为研究未见报道。本文利用VOF模拟气泡在花瓣形棒束通道内的上升过程,研究气泡在流道中的运动轨迹、形状和上升速度变化。
1 模拟理论及方法
1.1 计算模型
花瓣形棒束通道计算模型如图1所示,计算域截面外边缘为矩形,高度125 mm,其中包含4根呈矩形排布的花瓣形实心螺旋棒,花瓣形螺旋棒截面外切圆直径为D,外凸弧半径为R/2,内凹弧半径为R,D/R=5.2,外凸弧和内凹弧连接部分长为h,D/h=8.9,矩形流道边长为L,L/D=2.1,y轴方向为流动方向。已有研究[14-16]表明,燃料棒间距设置为0.5 mm时,可精确捕捉近壁面处流体的流场细节,而不会对燃料棒子通道整体换热情况产生影响。

图1 花瓣形棒束通道计算模型Fig.1 Calculation model for petal-shaped rod bundle channel
为了明晰气泡在花瓣形棒束通道内的行为特性,引入了相同工况下半径1 mm气泡在圆形棒束通道内的上升运动数值模拟,圆形棒束通道计算模型如图2所示,以燃料棒横截面积为基准,保证燃料体积不变,圆形棒与花瓣形棒放置在相同中心位置。

图2 圆形棒束通道计算模型Fig.2 Calculation model for circular rod bundle channel
1.2 VOF模型及控制方程计算模型
VOF[17]是通过计算模型中各相在划分每个单元网格内的体积分数和相应函数来确定相态之间的交界面,根据捕捉到的交界面进一步确定相间关系以及多相流的流动状态。每个计算单元中各相的体积分数(α)之和均为1.0,下角标g代表气相,l代表液相。气相体积分数方程如下:
(1)
式中:αg为气相的体积分数;vg为气相速度。
本文研究空气-水两相流体,对液相有:
αl=1-αg
(2)
假设气、液两相均为不可压缩流体,同时考虑流体的黏性,不与外界发生热量交换,其动量方程为:
(3)
ρ=αgρg+(1-αg)ρl
μ=αgμg+(1-αg)μl
(4)
式中:v为流体的速度;t为时间;ρ为混合相密度;p为压强;μ为流体的动力黏度;Fσ为流体所受到的表面张力。表面张力可通过CSF(连续表面力)模型[17]计算得出,将各相界面上的连续三维效应代表表面张力效应。CSF模型如下:
(5)
式中:σ为表面张力系数;ρ为混合相密度;κ为曲率。
1.3 边界条件及网格无关性验证
流体域液相设置为水、气相设置为空气,气泡区域设置空气体积分数为1,模拟条件设置为常温常压,inlet为速度入口、outlet为压力出口。设置初始气泡半径为1、1.25、1.5 mm,气泡初始位置设置在截面中心的左下方,距离中心4 mm,如图1b所示,气泡初始高度为4 mm,圆形棒束通道内气泡初始位置相同。计算模型考虑壁面影响,湍流模型选取SSTk-ω模型,采用PISO算法作为压力-速度耦合算法。
为了能够更好地捕捉气泡界面,对计算模型进行了结构化网格的划分,如图3所示。采用271万、347万、391万和427万网格数的网格进行无关性验证,并通过模拟得到气泡达到稳定速度时的气泡纵横比和气泡形状,如图4所示。由图4可看出,271万网格计算结果误差较大,其余3组的气泡纵横比和形状轮廓接近。综合考虑计算精度以及效率,采用网格数为391万工况开展数值模拟。圆形棒束通道网格如图5所示,网格数为212万。

图3 花瓣形棒束通道结构化网格Fig.3 Structured grid of petal-shaped rod bundle channel

a——不同网格数气泡稳定纵横比;b——不同网格数气泡轮廓对比图4 不同网格数量下气泡形状对比Fig.4 Comparison of bubble shapes under different grid numbers

图5 圆形棒束通道计算网格Fig.5 Calculation grid of circular rod bundle channel
1.4 模型验证
为了验证模拟结果的准确性,对气泡在静水中上升运动实验[18]进行数值模拟。气泡形状对比结果如图6所示。从图6可看出,气泡轮廓基本相同。气泡上升速度对比结果如图7所示,实验和模拟得到的气泡上升速度变化趋势基本相同。上述对比分析表明,本文所采用的数值模拟方法是可靠的。

图6 气泡形状对比Fig.6 Comparison of bubble shape

图7 气泡速度随上升高度的变化Fig.7 Variation of bubble velocity with height of ascent
2 模拟结果及分析
2.1 气泡轨迹
通过研究气泡的轨迹分布,可分析其对流道内传热性能的影响。不同尺寸气泡质心在花瓣形棒束通道内的运动轨迹坐标如图8a所示,气泡质心横向运动轨迹如图8b所示,图中y轴为纵轴,x、z轴为横轴,虚线代表流道中心线,叉号代表气泡碰触壁面。通过半径为1 mm气泡的运动轨迹可看出,气泡横向位移变化很大,由于花瓣形燃料棒的自螺旋结构,在气泡上升一段时间后,燃料棒的花瓣会扭转至流道中心,当气泡的横向位移达到一定程度时,会与壁面发生接触,并继续沿着壁面滑移。1.25 mm气泡运动轨迹与1 mm气泡相似,但其横向运动幅度较小。1.5 mm气泡沿螺旋轨迹上升并逐渐向流道中心运动,与1 mm和1.25 mm相比,气泡在上升过程中并没有接触到螺旋棒。综上可知,气泡尺寸越大,横向位移幅度越小。这是由于随着气泡尺寸的增大,气泡的升力减小,气泡所受到的横向作用力也随之减小[19]。

a——气泡质心三维运动轨迹;b——xz截面气泡质心运动轨迹图8 花瓣形棒束通道内不同初始尺寸气泡质心的运动轨迹Fig.8 Trajectory of bubble masses of different initial sizes in petal-shaped rod bundle channel
不同截面形状棒束通道内气泡质心的运动轨迹如图9所示。从图9可看出,与花瓣形棒束通道相比,圆形棒束通道内气泡的横向位移幅度更小,气泡在上升过程中所受壁面的影响更小。两个组件内的气泡均呈螺旋形轨迹上升,花瓣形燃料棒束通道内的气泡在上升一段时间后会碰触到燃料棒壁面,而圆形通道内的气泡在上升过程中逐渐靠近流道中心,不会碰触到壁面。综上所述,花瓣形棒束通道由于其结构特殊,与圆形棒束通道相比其对气泡的上升行为影响更大,且由于其内部的花瓣呈螺旋形,随气泡上升空间位置持续变化,导致气泡更容易受到壁面的影响,横向位移变化更加明显。
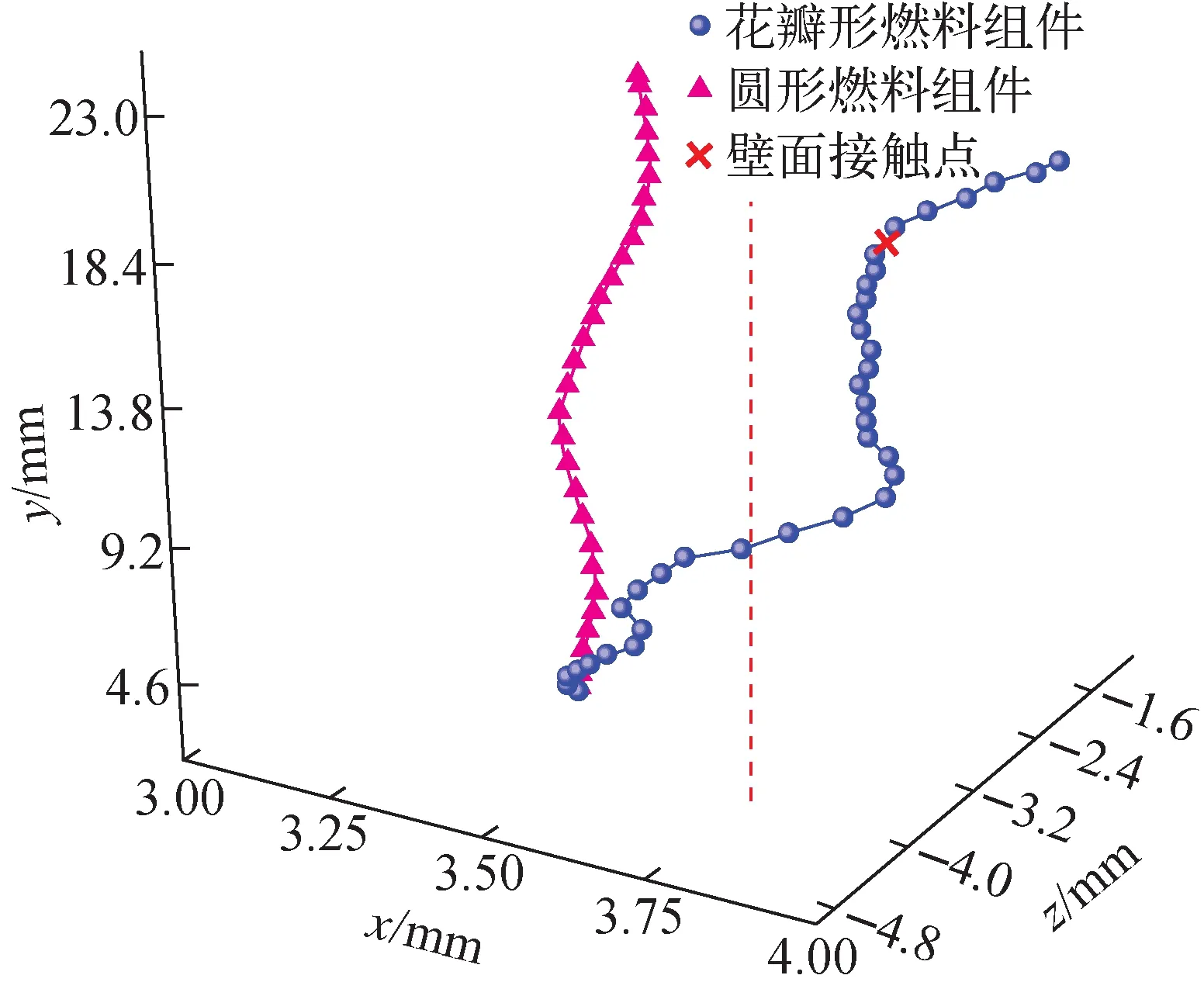
图9 不同棒束通道内气泡质心的运动轨迹Fig.9 Trajectory of bubble centre of mass in different rod bundle channels
要研究气泡的运动轨迹,需进一步分析气泡的受力影响。升力影响是气泡发生横向运动的主要原因,升力由黏性力分量和压力分量组成,与曳力方向不同,升力的方向一般与气泡运动方向垂直,其大小与气泡形状、流体性质及流体流速有关。气泡在棒束通道内运动时,由于通道内的壁面为曲面,流体流过时会产生非常复杂的流场以及壁面效应,导致气泡的运动行为及受力分析研究困难,因此主要采用泊肃叶流分析碰壁前单气泡所受升力。
在气泡升力公式中,升力系数决定了气泡升力的大小和方向,要研究气泡的升力首先应该了解升力系数的变化。根据Mehdi等[20]的研究结果,均匀剪切流下低黏度液体的升力系数公式为:
CL=0.001 307Eo3-0.019 79Eo2-
0.025 4Eo+0.590 1
(6)
式中,Eo为厄特沃什数,表征气泡所受表面力对气泡形状的影响,其公式如下:
(7)
式中:g为重力加速度;ρl为液相密度;ρg为气相密度;d为气泡水平直径;σ为表面张力系数。
Tomiyama等[21]通过气泡运动实验发现,气泡最大水平直径是导致气泡形状以及升力系数发生变化的主要原因,因此,计算Eo时采用气泡水平直径。图10为不同初始尺寸下气泡的升力系数和Eo变化。由图10可知,气泡在半径1~1.5 mm范围内时,其升力系数始终为正值,随着气泡初始尺寸的增大,气泡的Eo增大,同时其升力系数随之减小,据此可解释上文中气泡在上升过程中其运动轨迹随尺寸增大逐渐呈直线的原因。同时随着气泡的Eo增加,升力系数下降速度加剧,由以往的实验及模拟研究可知,随着气泡尺寸的增加,升力的作用方向会发生改变,即气泡尺寸过大时,升力系数会持续下降,与图10的升力系数变化趋势相同。
2.2 气泡形状
由气泡运动轨迹可知,气泡的形状变化是其在上升过程中会出现明显横向位移现象的主要原因,通过研究气泡的形状变化,可以解释气泡受力变化,从而阐明气泡的轨迹变化。本节通过不同尺寸气泡形状图、气泡纵横比和气泡相图,分析气泡形状的变化特性。
为了定量分析气泡的形状变化,引入气泡纵横比E,定义如下:
E=dh/dv
(8)
式中:dh为气泡的轴向长度;dv为气泡的径向长度;dh取气泡沿y轴的最大长度,而气泡横轴尺寸数据包括气泡截面上沿x轴和沿z轴的最大长度,二者数值基本相当,因此dv取二者平均值。
图11为不同尺寸气泡在花瓣形棒束通道内的三维形状变化。从图11可看出,气泡向壁面移动的过程中,在碰触壁面前,气泡形状逐渐由圆形变为椭圆形,这是由于气泡受到阻力和的影响,其上部与下部存在较大的压力差从而导致气泡发生形变;而气泡碰触壁面后会附着在壁面上,形状变得不规则。
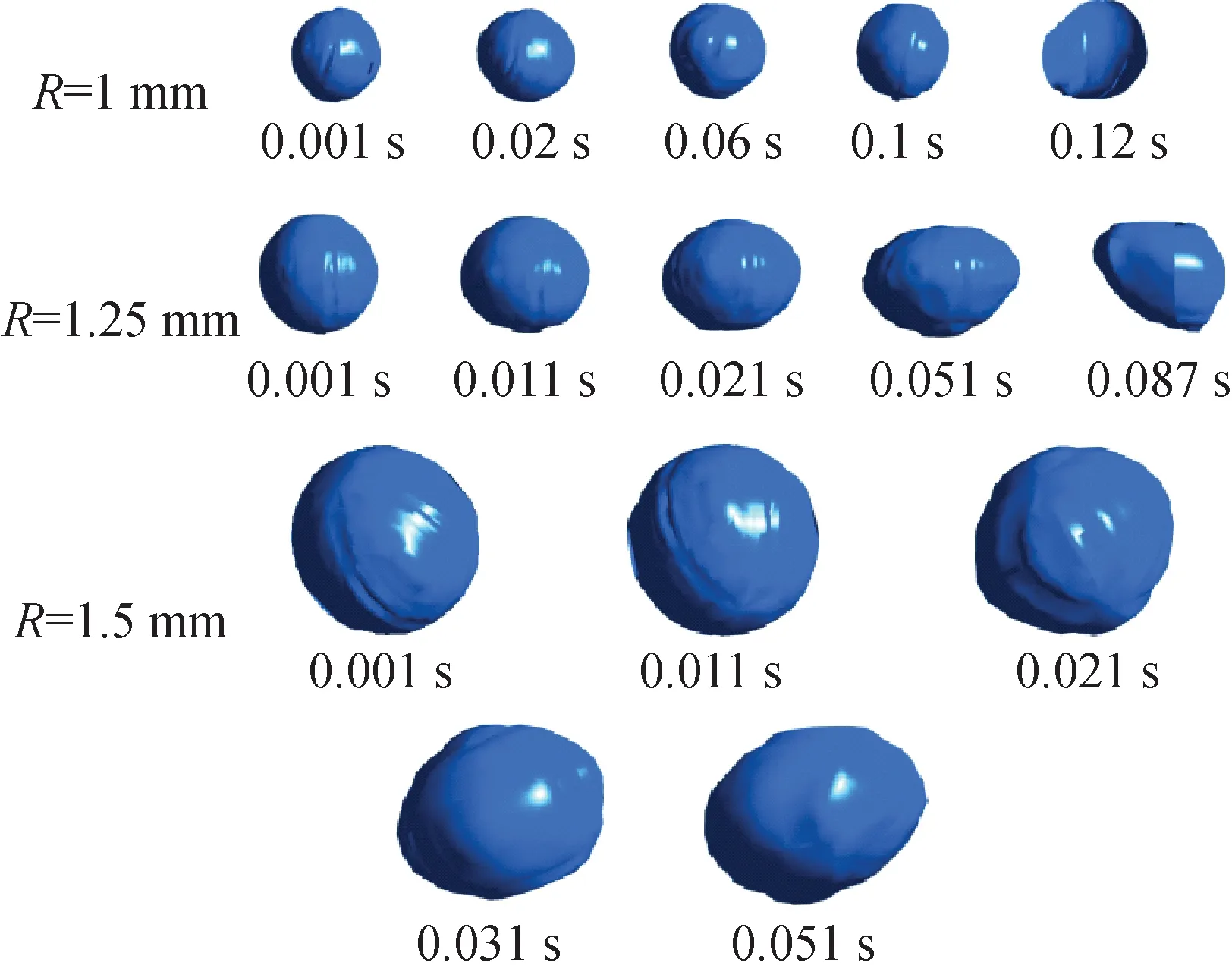
图11 不同尺寸气泡的三维形态变化Fig.11 Variation in three-dimensional morphology of bubbles of different sizes
图12为不同尺寸气泡纵横比的计算结果。从图12可看出,当气泡的纵横比大于1时,其在上升过程中会发生明显的形状变化,当气泡纵横比小于1后,气泡形状逐渐趋于稳定。1.25 mm气泡在运动初期纵横比迅速下降,气泡形状变化幅度非常大,0.03 s后气泡纵横比逐渐稳定,在0.07 s时气泡碰触壁面形状开始发生剧烈变化;在0.087 s时,气泡截面呈半圆状,此时气泡已经完全附着在壁面上,纵横比迅速上升。进一步观察不同尺寸气泡的形状及横纵比变化可看到,1 mm气泡在上升过程中,其形状始终接近圆形,纵横比变化幅度不大,维持在0.95左右,在其接触壁面后气泡局部会发生变形,纵横比发生波动。1.5 mm气泡纵横比变化幅度较大,纵横比最小可达到0.75,气泡在稳定后保持着扁椭圆状上升,纵横比在0.8左右,在不考虑气泡碰触壁面的条件下,1.5 mm气泡形状达到稳定的时间较1 mm和1.25 mm气泡的长。
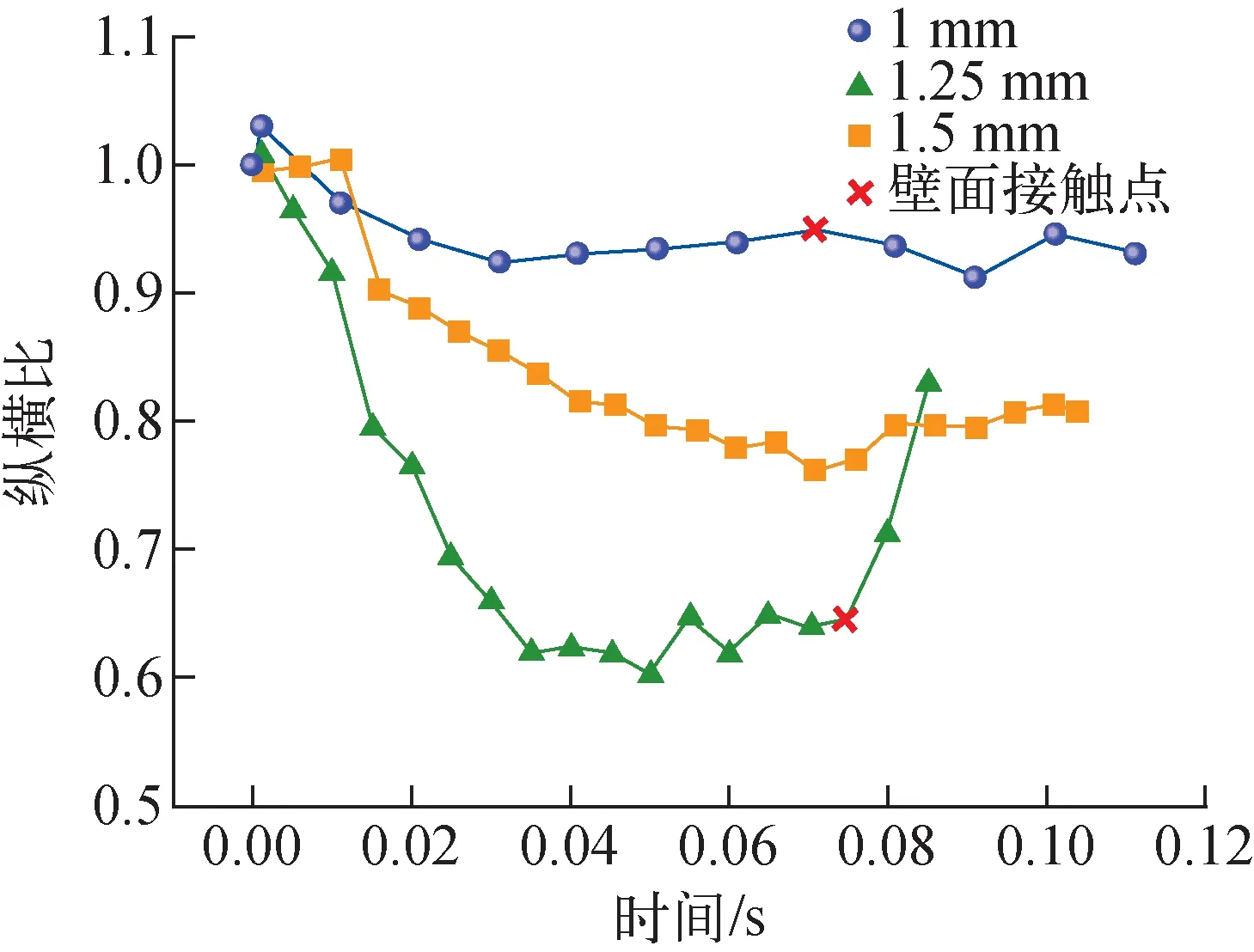
图12 不同尺寸气泡纵横比随时间的变化Fig.12 Aspect ratio of different bubble sizes over time
图13为不同棒束通道内气泡纵横比随时间变化。从图13可看出,在圆形燃料组件相比,在花瓣形燃料组件内,气泡的形变程度更小,纵横比变化更平稳。

图13 不同棒束通道内气泡纵横比随时间的变化Fig.13 Variation of bubble aspect ratio with time in different rod bundle channels
综上可知:在气泡碰触壁面前,其变形程度随着上升逐渐增大,纵横比随之减小,一段时间后气泡纵横比达到稳定,这是由于在气泡上升过程中,受其顶部和底部产生的压力差影响,气泡表面张力会发生变化,表面张力引起的气泡内部附加压强减小,从而导致气泡变形增大;在气泡碰到壁面后,气泡的形状变得不规则,纵横比也会随之发生变化。
2.3 气泡速度及其周围流场
通过研究气泡的上升速度变化,可阐明不同尺寸气泡在棒束通道内的流动与换热特性变化。气泡运动速度是衡量气泡行为的重要参数,对建立气泡换热机理模型具有重要意义,气泡速度主要取决于气泡尺寸和主流速度两个因素。为了得到气泡在每一时刻的上升速度,采用了DBSCAN聚类算法[22],并对模拟结果进行后处理,得到每一时刻气泡包含的所有相界面坐标点(α=0.5),通过计算可获得气泡在该时刻的质心坐标,计算公式为:
(9)

通过气泡的质心高度,可计算气泡的上升速度:
(10)
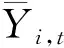
图14为不同初始尺寸气泡的轴向上升速度随时间的变化,叉号表示气泡开始接触壁面的坐标点。可见,1 mm气泡在初始阶段速度缓慢上升,一段时间达到峰值,随后气泡碰触壁面速度下降;1.25 mm气泡速度变化与1 mm基本一致,与1 mm气泡相比其稳定速度更大。1.5 mm气泡由于在上升过程中横向运动幅度不大,未接触到螺旋棒壁面,因此其速度不断上升,在0.05 s后逐渐趋于稳定。

图14 不同尺寸气泡上升速度随时间的变化Fig.14 Variation of bubble rise velocity with time for different sizes
综上,可将气泡在花瓣形棒束通道内的速度变化分为以下几个阶段:初始阶段,在浮力、曳力等的共同作用下,气泡速度从0开始加速上升,该过程持续时间很短。第2阶段,气泡的速度缓慢上升,并逐渐趋于稳定。第3阶段分为两种情况,若气泡未碰触到螺旋棒壁面,则该阶段气泡维持稳定速度上升,此时气泡受升力、曳力、浮力耦合作用,其形状和受力都不能保持固定,因此稳定速度在0.2 m/s附近振荡。若气泡碰触到壁面,此时气泡速度会迅速下降,随着花瓣形螺旋棒的花瓣部位慢慢旋转至流道中央,气泡碰触到棒束的壁面,所受到的黏性阻力增大,使气泡的速度逐渐减小。
通过对气泡周围流场及压力场分析,可阐明气泡上升轨迹和形状变化的原因,图15~17分别为初始半径为1 mm的气泡在相同时刻尾流变化图、气泡周围压力云图和气泡在流道内的位置。结合图15~17可看出,在初始阶段,t=0.001 s时,随着气泡速度的增加,气泡两端开始出现呈涡旋结构的尾流,此时气泡两端的速度场及压力场对称;尾流随着气泡的上升而逐渐上升,其速度始终小于气泡上升速度,因此尾流相对气泡下移,如图15中0.005 s时刻尾迹所示;在气泡上升时间到达0.01 s时,气泡两端的尾流开始出现不对称现象,气泡左侧的涡旋宽度逐渐大于右侧宽度,气泡也随之尾流变化向右侧偏移,形状也会发生剧烈变化,压力分布开始出现不对称特征;随后在0.02~0.04 s,气泡的速度逐渐增大,尾流逐渐变长,不对称现象越来越明显,气泡横向位移幅度也会增大,同时气泡周围压力场不对称现象加强,从图17可看出,这种不对称现象导致气泡在上升过程中发生横向位移;在0.06 s后,气泡的速度趋于稳定,气泡的尾流发生脱落后,开始形成新的尾流,此时气泡形状和轴向速度逐渐稳定,但气泡尾部压力场不对称现象越来越明显,导致横向位移速度增大;当气泡在t=0.1 s时刻附着在螺旋棒壁面上,气泡周围的流场也随之发生变化,导致靠近壁面的一侧气泡尾流变窄,同时气泡流速迅速下降,使远离壁面一侧的尾流相对气泡逐渐上升。气泡行为的变化是其尾迹和周围压力分布变化造成的,其中气泡尾部的流线变化更明显。综上,尾流首先在气泡两端对称产生,随着气泡速度增加逐渐脱落,尾流以及尾部压力场在气泡上升过程中呈现出非对称性,导致气泡的上升速度和轨迹也随之发生变化。非对称现象越明显,气泡横向位移幅度越大。

图15 不同时刻半径1 mm气泡周围流线变化Fig.15 Variation of streamlines around 1 mm bubble of radius at different moments

图16 不同时刻半径1 mm气泡周围压力变化Fig.16 Pressure variation around 1 mm bubble of radius at different moments

图17 不同时刻半径1 mm气泡对应位置Fig.17 Position of 1 mm bubble at different moments of radius
3 结论
本文利用VOF模拟了静水条件下花瓣形棒束通道内的单气泡上升行为,研究了气泡的上升轨迹、形状以及上升速度变化规律,主要结论如下。
1) 在花瓣形棒束通道内,初始半径为1~1.5 mm气泡的上升轨迹为螺旋形;气泡尺寸越小,横向移动越明显,因此气泡越容易碰到壁面,碰触壁面后气泡沿壁面滑移。未碰触壁面的气泡向中心移动,最后沿中心稳定上升。
2) 初始半径为1~1.5 mm气泡的形状均在球形和椭球形区域内波动。气泡接触壁面前,随着气泡逐渐上升,气泡的变形程度增大,纵横比减小并在一段时间后达到稳定;而在气泡碰触壁面后,气泡会附着在壁面上,形状变为半圆形,纵横比随之迅速减小。
3) 气泡在花瓣形棒束通道内的上升速度变化主要分为3个阶段:第1阶段气泡速度从0开始迅速上升,开始形成尾流;第2阶段气泡速度缓慢上升,气泡两端尾流及压力场发生不对称变化;第3阶段分为两种情况,如果气泡碰触壁面,其速度会迅速减小,靠近壁面侧的气泡尾流形状及压力场也会发生变化。若气泡未碰到壁面,气泡速度会在稳定速度附近波动,流场及压力场也会趋于稳定,尾流不断循环生成脱落。
4) 半径1 mm的气泡在圆形截面与花瓣形截面燃料棒棒束通道内均呈螺旋形轨迹上升,气泡纵横比的变化趋势也基本相同。但花瓣形燃料棒棒束通道内的气泡横向位移幅度更大且会碰触壁面,同时气泡形状变化程度更小。
