反应堆一回路对核主泵叶轮入流特性的影响

黎义斌,张帆,郭艳磊,李冬浩,王秀勇,王岩,杨从新,瞿泽晖

(1. 兰州理工大学能源与动力工程学院,甘肃 兰州 730050;2. 中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610213)

核电站一回路系统由并联到反应堆压力容器的3条封闭环路组成,是整个压水堆核电站的主干道[1-2].核主泵[3]相当于核电站的心脏,其主要作用是推动反应堆冷却剂在系统回路内循环流动,将反应堆堆芯产生的热量传递至蒸汽发生器,产生蒸汽带动汽轮机做功发电.核主泵是反应堆冷却剂系统中提供冷却剂循环动力的关键设备,其长期安全稳定运行对堆芯冷却和核电厂安全具有重要意义[4].

通常情况下,泵的叶片设计及安全可靠性评估均假设入流条件为均匀入流.众多研究人员在均匀入流条件下,对叶片泵的设计及运行进行了研究,获取了一定的成果[5-6].对于非均匀入流,研究者对发动机、压缩机、风力机等气体介质叶轮机械的研究取得了不少进展[7-9].目前,有关非均匀入流对核主泵入口流场影响的研究也有相关报道.侯向陶等[10]将SG下封头与RCP进行统一建模,分别研究了在稳态和瞬态情况下SG下封头对RCP入口流场的影响,与均匀入流相比,主泵入口处流场产生沿周向不均匀分布的轴向速度,且其扬程和效率分别下降了1.5%～7.7%和2.6%～4.1%.马腾跃等[11]开展了蒸汽发生器的缩比模型冷态试验,并以试验获得的数据作为SG下封头的入流条件,全面考虑了核主泵与蒸汽发生器的耦合流场特性,研究蒸汽发生器和核主泵流场特性之间的相互影响.叶道星等[12]通过试验和数值模拟方法分析了非均匀来流条件下核反应堆冷却剂泵的非定常特性,通过快速傅里叶变换和均方根法分析了压力脉动信号.

综上所述,仅考虑单一核主泵进行水力设计已不能满足反应堆一回路系统的设计要求.但是,目前核主泵水力设计仍采用均匀入流的设计理念,即便考虑了入流条件,也是简单的非均匀入流,且考虑了反应堆一回路系统对核主泵性能影响的相关研究较少.因此,文中将反应堆一回路系统进行模型简化,基于多孔介质模型和阻力匹配技术实现反应堆一回路系统的工况调节,采用CFD技术研究反应堆一回路对核主泵叶轮入流特性的影响.

1 几何建模及网格划分

1.1 几何建模

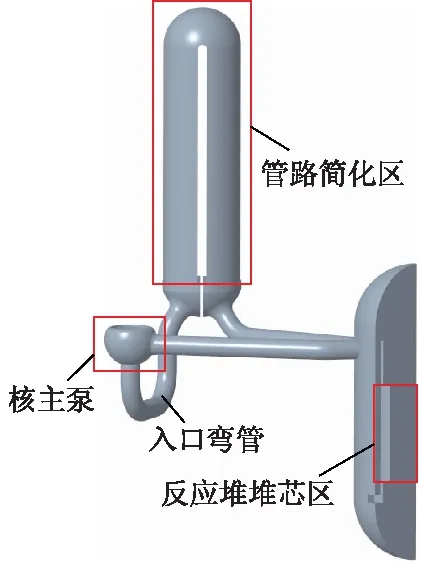
图1 反应堆一回路闭式系统简化模型

1.2 网格划分及无关性验证

应用ICEM CFD软件对计算域进行网格划分,考虑计算资源且为了保证计算模型有更好的收敛性,叶轮、导叶、压水室、进口段、入口弯管及冷热管段采用结构化网格划分,其余部分均采用四面体网格,其网格如图2所示.每个部件的网格数量:叶轮为3.16×106;进口段及入口弯管为3.25×106;压水室为3.99×106;导叶为2.93×106.最终,反应堆一回路简化模型的网格总数为3.34×107.对单独核主泵的计算网格进行独立性验证,以核主泵的扬程作为网格无关性验证的标准,发现当网格数达到1.20×107后,随着网格数的增加,核主泵的扬程值变化很小,此时可认为满足网格无关性的要求.

图2 计算域网格图

为了满足SSTk-ω湍流模型值的要求,取叶轮壁面第1层网格厚度为0.2 mm,边界层总层数为10,网格增长比率为1.2.计算得到叶轮叶片壁面y+值分布如图3所示.

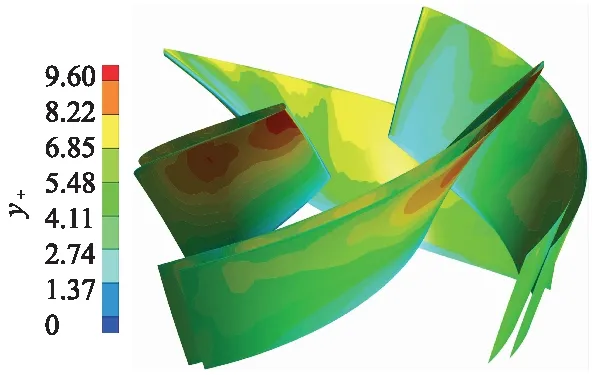
图3 叶轮叶片壁面y+分布

2 数值模拟

2.1 湍流模型及边界条件

数值计算的物理模型为反应堆一回路三维闭式系统,所以不需要单独设置进出口边界条件.设置计算域的对称面为“symmetry”边界,各部件的交界面均设置为“interface”,其余壁面均设置为无滑移条件,而近壁区的湍流流动选用标准壁面函数.由于叶轮部件为转动部件,故在计算时采用多重参考坐标系模型[14].计算模型采用SSTk-ω湍流模型,压力速度耦合方式选取SIMPLEC算法,离散选用易收敛的高阶格式,残差收敛精度设置为1.0×10-4,并结合入口流量判断结果是否收敛.

2.2 多孔介质模型

多孔介质模型就是在标准动量方程中增加了一个代表动量消耗的额外源项来实现流场调节[15],源项由2部分组成:黏性损失项和惯性损失项,计算式为

(1)

式中:Si(x,y,z)为i个动量方程中的源项;Dij为黏性损失系数;Cij为惯性损失系数;μ为黏度;vj为速度分量;|v|为速度大小.对于均匀多孔介质,式(1)可简写为

(2)

式中:D为黏性阻力系数,D=1/K,其中K为渗透率;C2为惯性阻力系数;vi为速度分量.

体积孔隙率γ表示控制单元内允许流体流过的体积与总物理体积的比值,计算式为

(3)

式中:V1为流体体积;V2为总物理体积.

阻力损失模型在CFX中包含2种损失模型,分别为各向同性损失模型和定向损失模型.流体进入反应堆堆芯和U型管束后,其主流方向分别为堆芯轴向和U型管束轴向,不会产生径向流动和损失,使得多孔区域的流动与真实堆芯及U型传热管的流动更接近,进而保证模拟的压降更精确.因此,文中选择定向损失模型来描述这一特征,并采用多孔介质最基本的阻力计算方法“渗透率和损失系数”对多孔介质区域的阻力进行计算.

渗透率K即流体通过多孔介质区域的渗透能力,其基于Darcy定律来描述多孔介质区域的渗透特性,计算式为

(4)

式中:Q为通过多孔介质的体积流量;L为流通长度;A为横截面积;Δp为压差.

损失系数Kloss表示流道内摩擦阻力损失与局部损失之和,其流动方向上的计算式为

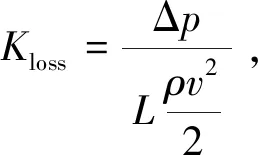
(5)

式中:Δp1为流道内摩擦阻力损失;Δp2为局部损失.

为了使得瞬态计算更快更好地收敛,以稳态计算结果作为瞬态计算的初始条件,进行非定常数值模拟.在综合考虑瞬态计算稳定性和计算精度条件下,以叶轮叶片旋转3°作为时间步长,即叶轮叶片经过120个时间步长旋转1周.总的计算时长为叶轮旋转18周所用的时间,即0.727 27 s,为了保证计算结果的准确性,文中统一选择最后1圈的计算结果进行瞬态分析,叶轮的转速为1 485 r/min,叶轮轴频fR为24.75 Hz,叶片数为4,叶频fRPF为99 Hz,叶轮通过频率fSPF为272.25 Hz.

为了获得入口弯管的压力脉动信息,自下封头出口至主泵入口段在各截面中心位置各取1个监测点,分别命名为xrg1—xrg6,各监测点的具体位置如图4所示.

图4 监测点位置示意图

为了更为全面准确地比较分析压力脉动的大小,采用量纲为一的系数Cp来替代监测点的压力值,其表达式为

(6)

(7)

式中:pi为监测点流场瞬时压力;pout为叶轮出口平均压力;ρ为流体介质密度;u2为叶轮出口处的周向速度;D2为叶轮出口平均直径;n为模型泵的转速.

采用量纲为一的频率系数Cb来代替频率,其公式为

(8)

式中:f为频率.

3 试验验证及性能预测

3.1 泵外特性试验

在0.6Qd～1.3Qd流量工况下,基于CFD技术对核主泵缩比模型的水力性能进行数值预测,并将数值预测结果与试验结果进行对比,以验证数值计算方法的合理性,进而保证模拟结果的可靠性.图5为闭式试验系统示意图,核主泵缩比模型扬程和效率计算值和试验值的对比结果如图6所示.相比试验值,数值预测得到的扬程和效率误差均小于5%,表明数值预测精度吻合度较好,根据相似换算关系,核主泵性能参数可以满足设计要求.

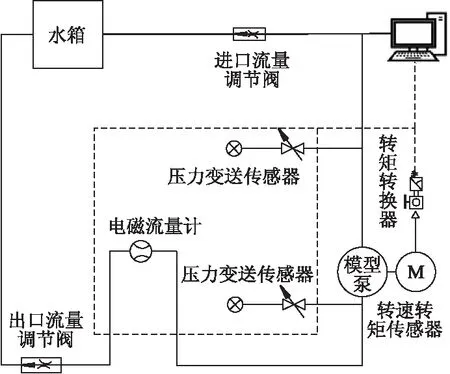
图5 闭式试验系统示意图

图6 计算结果与试验结果对比

上述试验忽略了反应堆一回路系统对核主泵水力性能的影响,即没有考虑反应堆一回路中核主泵来流的非均匀性或核主泵缩比模型试验台的来流不均匀性.因此,相比核主泵的实测值,上述单一核主泵缩比模型的数值预测扬程值和效率值均偏大,其数值误差可以通过上述数值预测和试验进行修正.

3.2 泵及管路性能预测

根据设计流量,采用不同的质量流量进口在0.6Qd～1.3Qd的8个流量工况点对核主泵及管路进行性能预测,得到泵特性曲线与管路特性曲线,如图7所示.在泵特性曲线与管路特性曲线的交点处,主泵所提供的扬程被管路系统所消耗,二者达到平衡.此时,闭式系统主泵的流量与额定工况值相差0.998%,扬程与额定工况值相差3.76%,二者误差较小,符合整体简化要求.

4 CFD数值模拟结果及分析

4.1 入口弯管计算结果及分析

图8为入口弯管不同截面的压力分布云图.由图可以看出,弯管截面的压力分布特性被破坏,在截面W1处受管道曲率的影响较小,但是受到反应堆一回路系统的影响,有明显的旋涡出现;在截面W2和W6处流体的流动方向发生变化,且受到弯管曲率及离心力的影响,外侧壁面的曲率半径由小变大,离心力指向外侧壁面,进而使得流体所受到的离心力和压力产生叠加效应,从而使得流体在外壁面的压力增大,而靠近内壁侧压力较小,进而产生横向压差.随着流动的发展,低压区范围越来越大.在管壁周围压力较小,而高压区集中在弯管中心.当流体流至弯管出口靠近泵进口位置的截面W7时,流体压力分布进一步恶化,低压区范围进一步增大且低压区由弯管内壁面向外侧壁面移动.

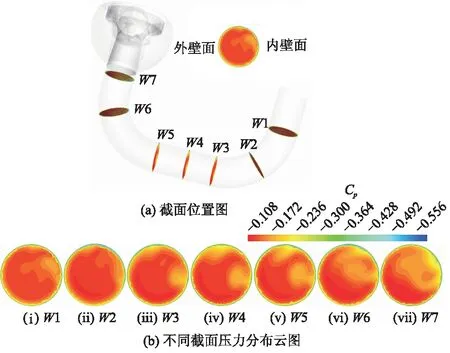
图8 入口弯管不同截面的压力分布云图

图9为入口弯管不同截面处的速度及其流线分布云图.由图可知,在一回路系统的影响下,流体在弯管内速度呈现不均匀分布,出现复杂的扰动涡团.截面W1靠近蒸汽发生器下封头,由于其非对称的突缩结构,使得从该处流出的流体较为混乱,并且在管壁内侧有明显的旋涡结构出现.在截面W2和W6处流体进入弯肘段,受离心力作用和曲率差的影响较大,使得该位置处的流场流动特性十分复杂,并产生了典型的反向涡对.当流体流过中间直管段到达截面W4时,内壁的低速区域汇入主流,在截面W7处横向流动开始变得明显,但速度仍然呈现非对称分布,同时出现了“Dean”涡对,这是一种管内二次流现象.

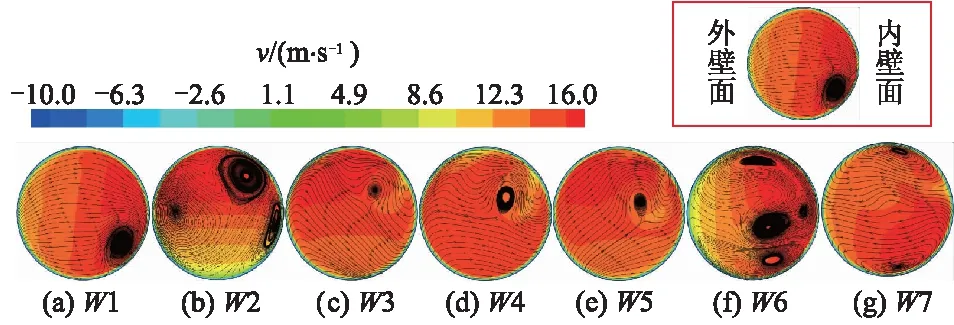
图9 入口管路不同截面的速度和流线分布图

图10为额定工况下入口弯管在一个旋转周期内各测点的压力脉动时域和频域特性图.由图10a可知,同一测点在不同时刻呈现一定的非定常特性,在转子旋转1周时间(1T)内,各个监测点的压力又呈现明显的周期性特征,各个监测点均出现4次波峰及波谷,并且在每个波峰及波谷之间,又出现明显的次波动,主要是由于反应堆一回路系统下入流畸变二次流现象使得流道出现堵塞,形成局部高压.由图10b可知,各测点的频率分布相似,经计算可知,主频的脉动峰值均为297 Hz,等于转频的倍频,同时在叶频处出现次频脉动,说明整个入口弯管中的压力脉动明显受转子转动效应的影响.

4.2 核主泵入口流场计算结果及分析

为了研究反应堆一回路系统对核主泵叶轮入口流场的影响,在叶轮进口前取5个等距截面进行流场分析.在截面P3上取A,B,C这3条圆弧线,分别为核主泵进口管内径的0.4,0.6和0.8倍.具体位置如图11所示,图中ω为角速度.

图11 核主泵入口截面示意图

图12为核主泵入口截面P3处速度流线图.可以观察到,在反应堆一回路系统的影响下,核主泵入口处形成了1对旋涡,且这1对旋涡的回旋方向相反,从而导致主泵进口产生预旋,而均匀入流条件下,入口截面的速度流线呈周向对称分布.

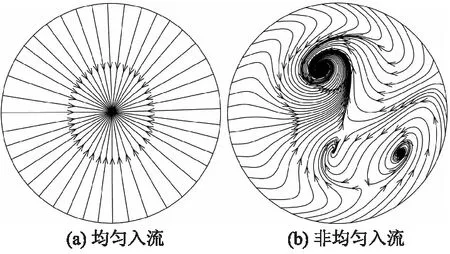
图12 核主泵入口流线图

图13为核主泵入口处不同截面上的压力分布.由图可知,入口流动不再沿轴向进入叶轮,各截面压力呈现不均匀分布,且存在一个明显的局部低压区.在截面P1至P5流动发展的过程中,高压区变得越来越明显,且向截面中心移动.各个截面存在明显的压力梯度,表明上游弯肘对泵入口压力产生了影响.由截面P5的压力分布可知,流体在截面P4至P5流动过程中,受转子旋转以及流体不断被吸入流道的影响,局部高压得到释放,且由于流体和轮毂凸起之间的挤压,使得该截面中心处压力值较高,从中心沿径向的压力梯度在周向上呈现不均匀分布,从而对转子径向受力产生不利影响.

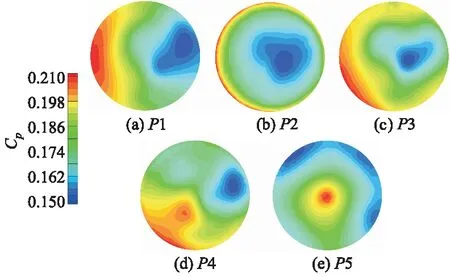
图13 核主泵入口截面压力分布

图14为核主泵进口不同截面处的速度分布.

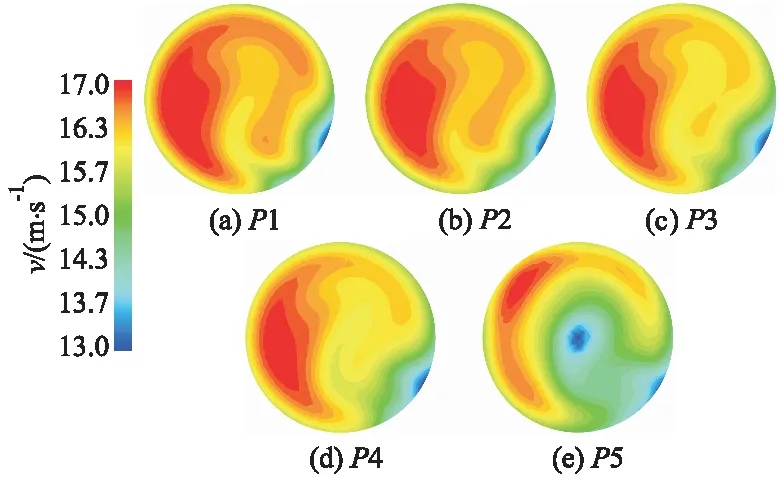
图14 核主泵入口截面轴向速度分布

由图14可知,轴向速度的对称分布特性被破坏,在弯肘内侧存在明显的低速区域,而外侧速度较大,速度分布整体趋于相似且存在偏心.随着流动发展,流体距离核主泵入口越近,低速区变得越来越明显,且不断向弯管中心移动,高速区在缓慢减小,在截面P5处低速区范围最大,在截面中心出现低速区,受主泵对其入口流场整流作用的影响,流场的紊乱程度降低.

为了定量描述轴向速度在核主泵入口处的分布规律,数值计算发现截面P3处轴向速度沿周向和径向的分布存在明显的不均匀程度,如图15所示,图中θ为角度;x/R代表x所在直径的距离与核主泵进口管内径的比值;y/R代表y所在直径距离与核主泵进口管内径的比值.

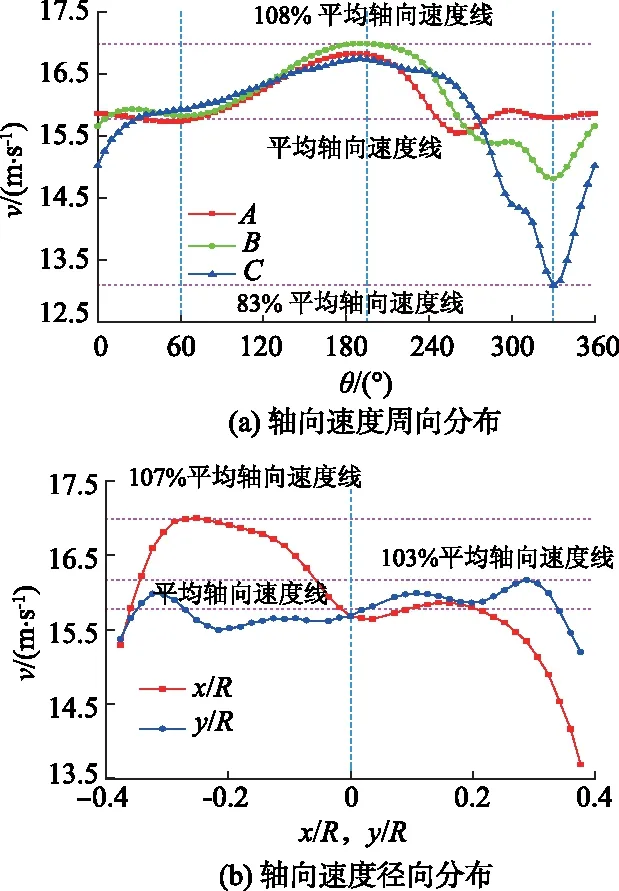
图15 核主泵入口截面轴向速度沿周向和径向分布

由图15a可知,轴向速度沿圆弧线A,B,C的分布是相似的,在60°～180°和330°～360°,3条圆弧线均有一个上升的变化;在195°附近轴向速度达到最大值,此时偏离平均轴向速度108%;而在195°～270°,这3条圆弧线都有一个减速区,同时圆弧线C在300°～360°区域的轴向速度最小,其最小轴向速度低于平均值83%.由图15b可知,沿径向速度分布较平均轴向速度也有一定程度的偏离,沿x所在直径的最大轴向速度为平均轴向速度的107%,而沿y所在直径的最大轴向速度为平均轴向速度的103%.通过分析可知,各截面均存在一个明显的局部低压区,且沿周向和径向的速度变化均超过了平均轴向速度的80%.MAHAFFEY等[16]指出,离心泵的吸入口处沿圆弧线的速度分布应在其平均速度的±5%内,而沿径向的速度分布应在其平均速度±10%内.可见,在反应堆一回路系统的影响下,核主泵入口处产生了严重的入流畸变.

5 结 论

1) 基于SSTk-ω湍流模型的数值模拟结果与试验结果的吻合度较高,在全流量工况下验证了数值计算的准确性.在反应堆一回路中采用多孔介质模型,通过泵特性曲线与管路特性曲线的动态匹配,可实现管路阻力的静动态调节,使核主泵在反应堆一回路系统中运行在额定工况点.

2) 反应堆一回路系统对核主泵内部流动和性能有显著影响,核主泵入口弯管流动的周向对称性被破坏,压力和速度呈现不均匀分布,流体在运动过程中,受到弯管曲率的影响,在离心力作用下形成了管内二次流动,且二次流动由弯管内侧不断向弯管中心偏移,在靠近叶轮进口处产生了“Dean”涡对,因此在后续的研究中将考虑增加入口弯管与核主泵叶轮之间的距离来缓解这一现象.

3) 在反应堆一回路系统的影响下,核主泵入口流场产生了1对旋转方向相反的旋涡,其压力和速度的周向均匀分布特性被破坏,各截面均存在一个明显的局部低压区,且沿周向和径向的速度变化均超过了平均轴向速度的80%,这一现象对核主泵叶轮做功及受力产生不利影响,使核主泵的水力性能下降.因此,核主泵叶轮的水力性能受到反应堆一回路的影响不可忽略,设计和模型换算过程中要考虑上述影响,否则会导致实际运行过程中核主泵的水力性能不能满足反应堆一回路系统的参数要求.