基于变分模态分解的癫痫脑电芯片算法研究

王 婷,石 蓝,黄 玮,张子辰

(江苏信息职业技术学院,江苏 无锡 214000)

0 引言

癫痫是一种常见的神经系统疾病。目前,被癫痫疾病影响的人数全球超过5 000万人[1]。头皮电极获得的脑电图(EEG)、磁共振成像和计算机断层扫描等影像技术结合使用,是癫痫诊断的常规方式[2]。在传统的癫痫检测中,医学专家观察脑电图是否包含癫痫特征波,这种方法不仅耗时,而且高度主观依赖经验。脑电图中存在的大量噪声可能会干扰专家的判断。设计脑电的可穿戴式检测芯片的算法,可以自动检测患者的癫痫发作情况,从而高效地协助医生进行诊断。

在癫痫信号特征提取阶段,为了达到良好的特征区分和数据降维效果,国内外已经进行了多种提取方式的探索。基于经验模态分解的变分模态分解主要思想是将信号分解为围绕各中心频率附近变化的窄带变分模态分量,通过寻找约束变分模型的最优解来自适应获取变分模态函数(VMF)。发作期脑电的不确定度会明显降低,出现了许多与熵(En)有关的脑电特征提取研究方法,主要包括近似熵、样本熵、模糊熵[3-4]。精细复合多尺度散布熵是在散布熵的基础上对信号进行多尺度量化得到的,避免了原始散布熵因仅在单一尺度上处理信号而出现的复杂性导致特征提取不完全等问题[5]。

虽然已有许多特征提取方法和分类方法运用于癫痫检测中,但大多是针对癫痫发作期脑电与正常脑电的二分类。而对于癫痫患者不发作时进行的检测也是有必要的,即发作间期的检测。发作期间的脑电图通常也可见异常的癫痫样放电。因此,本文主要研究正常时期、发作间期与癫痫发作期3类脑电信号的检测。发作间期的脑电图部分由慢波化组成,若基本节律中混有较多的慢波,则形成不规则的脑电图。针对发作间期的背景节律性特点,本文提出一种基于变分模态分解的癫痫检测算法。EEG信号经VMD分解后获得变化中心频率的VMF,对VMF进行能量分离,加强慢波、棘波等特征,再二次提取其均值、方差和RCMDE 3种特征,并利用随机森林对其进行分类,完成了正常脑电信号、发作间期与癫痫发作期的3分类。通过与文献方法对比,本研究验证了该方法提取EEG信号的有效性。

1 方法

图1为本文提出的基于变分模态分解的癫痫脑电信号检测算法的流程图。本方法包括如下4个步骤:(1)对脑电信号数据集进行VMD分解,分解为有不同中心频率和带限的固有模式函数多个子模态;(2)对子模态进行能量分离,增强信号瞬态冲击成分;(3)经过能量分离后的信号二次特征提取其均值、方差和RCMDE;(4)将提取的特征输入随机森林进行分类。

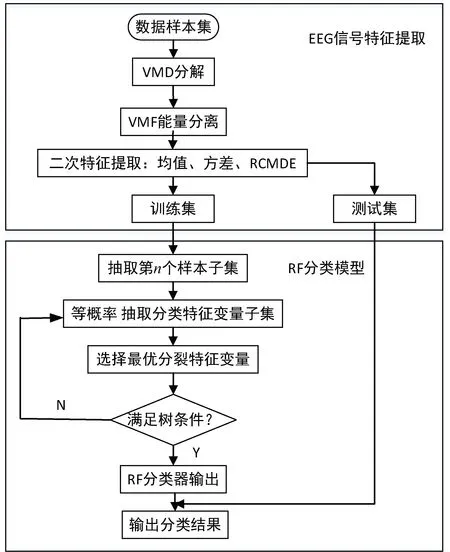
图1 癫痫检测流程

1.1 变分模态分解

变分模态分解是自适应、完全非递归的数据处理方法。它是根据当前数据来确定信号序列的模态分解个数,可以自适应对每种模态的最佳中心频率和有限带宽进行变化,有效地对固有模态分量进行分解。它的核心思想是构建和求解变分问题。由于EEG测试时间以及被测样本的不同,各频带段中心频率也会发生小范围的改变,VMD并不是固定的中心频率,而是将EEG信号分解成在中心频率附近的变分模态分量,不断迭代的中心频率可以良好表达这种神经活动的轻微变化。VMD 算法中惩罚因子可以保证高斯噪声环境下信号重构的准确性,其值过大会引起模态重叠,较小会引入噪声,默认将其设定为2 000。分解模态个数K对序列分解和预测精度都有较大影响,若K值过大会造成过分解,产生无用分量,高频模式过多,增加计算复杂度。若 K 值过小,序列将不会完全分解,使部分带限信号分解不出来造成原信号信息的丢失,进而影响分析结果。脑电信号的癫痫异常信息大多在25 Hz以下,根据中心频率观察法选取分解模态个数K=4。对数据集A010、D010、E010前1 000个数据进行VMD分解,癫痫信号特征波主要集中出现在子频带 VMF2～VMF4内。故在后续的特征提取工作中,仅分析 VMF2～VMF4频带内的脑电信号。

1.2 能量分离

Teager能量算子是一个非线性算子,可以对被测信号相邻的3个采样点进行计算,具备优良的时间分辨率,计算过程简单快速,能够增大癫痫波特征频率的倍数。对正常脑电信号数据集中的A010、癫痫发作间期D010 以及癫痫发作期E010 经VMD分解后,将VMF2～VMF4 频带信号进行Teager 非线性能量算子计算后,正常脑电信号的Teager能量较为平缓,在0～700 μA范围内波动。癫痫发作间期,脑电信号的间歇性突增最高达7 000 μA。癫痫发作期时,能量在棘波处波动非常剧烈,可达2×105μA。经过Teager能量分离后,3种EEG信号的特征更加明显,其中每组信号的四频带信号最为敏感,所以只选取正常EEG、发作间期EEG、发作期EEG的四频带的能量作为后续二次特征提取。

1.3 二次特征提取

根据以上分析,信号经能量分离后的四频带能量包含脑电信息的重要组成部分,接下来将对四频带能量进行二次特征提取,分别提取均值、方差与精细复合多尺度散布熵。RCMDE用来表征TEOV4时间序列的复杂性,人脑非致痫区域的神经活动相对致痫区域更活跃,通过RCMDE可以更好地观测EEG的规则性和组织性,计算 RCMDE 需要对4个参数分别设置:类别个数c,嵌入维度m,时间延迟d以及尺度因子τ。类别个数c若过大会导致具有较大差异的两个量被归为同一类,过小则导致具有较小差异的两个量被归为不同类,此处将c值设为 6。对于嵌入维度m,为了保证统计可靠性,将m值设为 3。时间延迟d一般取 1,本文尺度因子τ设为 10,即每个数据段提取10个尺度上的 RCMDE 值。利用RCMDE计算能量算子结果如图2所示。

图2 不同EEG的RCMDE

患者在癫痫发作期间产生的棘波和尖波等波形具有节律性,在0～10时间尺度上,正常EEG的RCMDE都要大于癫痫患者EEG的RCMDE,发作间期的脑电信号幅值变化最小。在脑电图中的潜在的脑电模式未知的情况下,相关的时间尺度也是未知的。通过RCMDE将脑电信号扩展到10个时间尺度,有利于在时间尺度未知时提供特殊的观察视角。有可能某一时间尺度上,正常脑电信号的熵值与癫痫信号的熵值接近,但在其他时间尺度则会有明显差别。RCMDE可以增加癫痫判断容错率,进一步利于构建后续脑电信号分类模型。

1.4 随机森林算法

随机森林算法(Random Forest,RF)基本单元是决策树。每棵树都可以视为单个分类器,分类输出由所有决策树投票。RF通过自助抽样和随机子空间,能够对多维度、多特征的数据进行快速分析以及提高分类性能,将提取的三维特征作为随机森林输入,首先假设N为训练集中的事例数,则从训练集中随机抽取N个样本,有放回在每个样本过程和获取的N个训练样本中。从m个特征变量中随机等概率抽取d个子变量,这些子变量组成此节点的分裂特征变量子集,然后利用基尼系数值最小原则选择一个最优的分裂特征变量继续对该节点分裂,建立多个决策树组合为随机森林。针对测试的数据集,每个决策树都会得到一个分类结果,对这些结果进行投票表决,得票数最多的分类结果为最终决策。

2 实验与分析

实验数据来自德国Born癫痫脑电研究室。此数据集中共包含标号从 A～E的 5个子数据集,每个子数据集均包括100个脑电信号。每个脑电信号的长度为 23.6 s,采样频率为 173.6 Hz。

由于EEG是非线性和非稳态的信号,传统的频域分析方法只能揭示EEG信号的整体特征。而癫痫的特征波可能会在瞬间出现。为了捕捉脑电信号的瞬时行为,本研究通过使用VMD将原始EEG信号分解为4个数量的子模态。子模态中的癫痫特征信息此时仍然受背景噪声的干扰,冲击成分不明显,采用能量分离对癫痫特征起到增强的作用。为了减少运算,本研究选择最敏感的能量分布TEOV4作为后续提取特征。在TEOV4中提取均值、方差和RCMDE3类数据特征作为后续随机森林的分类特征。随机森林的分类性能与决策树的数量有关,当树的数量少于100棵时,误差会迅速减少,而当树的数量大于250棵时,误差会保持温和的浮动。因此,在接下来的实验中,随机森林的决策树数量被设定为250棵。

在脑电信号数据集中,随机抽取70%的脑电信号作为训练集,30%作为测试集,随机森林中包含250棵决策树。表1显示了分类器的准确度 (ACC)、灵敏度 (SEN)和特异性 (SPE)3个评价指标。

表1 与其他算法结果对比

本文针对正常EEG、发作间期EEG、发作期EEG进行三分类,而表中两种算法是针对发病与非发病的二分类研究。Acharya 等[6]采用熵等23个特征进行脑电分类获得87.93%准确度,Bhattacharyya 等[7]基于可调Q小波变换提取多元模糊熵方法对脑电信号处理获得了84.67%准确率。实验结果表明,本文算法在ACC、SEN、SPE都在一定程度有所提升,证明该方法对于脑电信号分析具有可行性。

3 结语

由于用癫痫脑电记录进行人工诊断是一种低效的方式,本文提出了一种基于变分模态分解的癫痫脑电信号可穿戴芯片的检测算法。应用能量分离,对VMD分解后的信号序列进行特征信息增强,从中提取均值、方差和RCMDE 3种特征,并通过随机森林进行自动预测,分类了正常时期、发作间期与癫痫发作期3类脑电信号。实验结果显示本文所提出的方法分类准确度90.78%,可以辅助临床医生进行诊断,具备潜在临床应用价值。