半潜式风电机组平台水动力模型试验及数值模拟研究
2023-10-25翟恩地李荣富赵子晗邵昌盛章丽骏
方 龙,翟恩地,李荣富,赵子晗,邵昌盛,章丽骏
半潜式风电机组平台水动力模型试验及数值模拟研究
方 龙1, 2,翟恩地2,李荣富2,赵子晗3,邵昌盛3,章丽骏4, 5
(1. 天津大学建筑工程学院,天津 300072;2. 北京金风科创风电设备有限公司,北京 100176;3. 南方海洋科学与工程广东省实验室(湛江),湛江 524002;4. 上海交通大学船舶海洋与建筑工程学院,上海 200240;5. 东海实验室,舟山 316021)
针对某深远海漂浮式风电机组运动响应受风载荷影响的问题,进行了缩尺模型的水池试验以及实尺模型的数值模拟计算:根据水池自由衰减试验得到的自由衰减曲线及衰减消灭曲线,对基于势流边界元建立的数值模型进行了必要的阻尼修正;用数值方法计算得到的平台运动RAO结果与水池试验生成白噪声非规则波时测量得到的平台运动响应结果进行了对比分析,确保了所建立数值模型的准确性,同时验证了白噪声非规则波试验的可行性;通过时域及频域数值计算方法与试验方法相结合,对比研究了恒风条件下和无风条件下白噪声非规则波作用时平台的运动响应,以及相关的波浪载荷与风载荷的幅值与相位频谱.根据上述计算及研究结果,最终初步总结出了风载荷对风电平台半潜式浮式基础的运动响应的主要影响形式及原因.研究结果表明:风载荷对平台运动的影响与风、浪载荷主要频率成分处频率、幅值以及相位有关.在风载荷与波浪载荷的能量集中频率基本一致,且与平台运动固有频率相重叠时,风载荷的影响会得以显著体现(本文中差异约22%),而影响的形式(增强或削弱运动幅值)则取决于此时风载荷与波浪载荷的相位差:当风、浪载荷同相位时,联合载荷作用下相关自由度的运动幅值将显著增大,反之则显著减小.
浮式风电机组;运动响应;气动载荷;模型试验;数值模拟;势流边界元
海上风电近年来快速发展[1],但随着近海风力资源开发日趋饱和加之近海船舶航道、渔业的开发,海上风力发电朝深水发展的趋势成为必然[2].因此,自Heronemus[3]于1972年首次提出漂浮式风电机组(floating offshore wind turbines,FOWT)的概念以来,越来越多的学者开始研究与漂浮式风电机组相关的工程与学术问题.与近海固定式风电机组相比,对漂浮式风电机组相关问题研究的最大特点和难点是风电机组浮式基础复杂的运动响应问题,这也是影响漂浮式风电机组气动性能的一个关键因素.
现有相关研究中,主要以基于数值分析程序的研究方法为主:Jonkman等[4-5]基于FAST的水动力模块HydroDyn进行了二次开发,对驳船式浮式风电机组进行了气动-水动-伺服-弹性全耦合数值分析,并与另两型TLP以及Spar基础漂浮式风电机组进行了对比研究;Kvittem等[6]则利用非线性水动-气动耦合程序Simo-Riflex-AeroDyn对不同水动力计算方法对半潜式漂浮式风机运动响应计算结果的影响规律进行了对比研究.此外,也有部分学者致力于针对漂浮式风电机组开发独立计算程序:Meng等[7]利用独立开发的程序针对某型6MW漂浮式风电机组的运动响应开展了时域数值模拟研究.受限于试验成本以及早期对浮式基础风电机组发展的不够重视,与漂浮式风电机组相关的试验研究则相对较少.Goupee等[8-9]与荷兰MARIN合作,对柱式、TLP型以及半潜式基础漂浮式风电机组运动响应特性进行了模型试验研究.
随着近年海上风电机组在中国沿海海域的快速发展,漂浮式风电机组的发展需求在中国也日趋迫 切[10],针对漂浮式风电机组复杂的气动-水动耦合作用,国内也有大量学者开始进行相关研究:马钰[11]基于5MW OC3-Hywind浮式风机平台进行了全耦合时域运动响应数值计算;张靖晨等[12]利用MATLAB开发的计算程序分别基于叶素动量理论和势流理论,针对某型浅吃水的5MW Spar型漂浮式风电机组基础的运动响应进行了数值计算分析.然而,全耦合方法费时费力且仍需试验结果来验证其可靠性,势流理论与叶素动量理论皆为简化方法,无法考虑强非线性对计算结果的影响.若能结合模型试验与数值方法来研究复杂的气动-水动相互作用的机理进而改进现有算法,则有望提高数值方法的计算效率以及准确性.国内也有少量针对漂浮式风电机组基础运动响应的试验与数值对比研究,如阳杰等[13]针对6MW单柱型漂浮式风电机组在极限海况下的运动响应开展时域数值与试验对比研究,验证了数值方法的准确性.
目前已有大量针对浮式风电机组基础运动响应的研究,但其中数值与试验相结合的研究仍较少,且大部分试验数据不公开[14].此外,尽管国外已有不少更大装机容量浮式风电机组的研究和建设项目[15],但目前国内建成的浮式风力仍然以6MW容量为主.在此背景下,本文基于本研究团队在MARIN进行的6MW半潜式风电机组基础风洞水池试验结果,进行了试验与数值对比研究,并结合数值方法探究了风与波浪载荷耦合作用下半潜式漂浮式基础运动响应机理,研究成果可为国内同类型漂浮式基础模型试验与运动响应模拟分析提供参考依据,并对国内漂浮式风电机组的大规模商业化应用提供指导.
1 风洞水池试验
1.1 试验水池
本次研究相关的模型试验在荷兰MARIN的海洋水池(offshore basin)完成[16],水池长44.35m,宽35.6m,水池深度1~10m并可调节.水池可以模拟规则波、非规则波、白噪声非规则波,并可同时模拟风浪流作用.
1.2 试验模型
试验模型根据金风科技设计的半潜式浮式风电机组的浮式平台基础选择1∶55的缩尺比制造,试验模型如图2所示,对应于该缩尺比下的各参量相似比见表1,通过表中相似比可将模型试验设置的参数以及试验结果的数据换算为浮体实尺情况下的结果.此外,在模型试验中,平台运动通过6自由度运动捕获系统获得,该系统由浮体平台表面的3个感光贴片和多个光感相机组成;波面升高数据则由置于平台中心附近波高仪记录所得.
试验用风力机模型理论上应该根据雷诺相似进行缩尺,但是这会与浮体的缩尺之间无法保持一致,因此最终试验用的是金风科技设计的专用的低雷诺翼型.此外,锯齿形胶带还被添加到叶片的吸力侧以获得湍流边界层,并用电动机驱动风力机模型来匹配真实风力机的转速与推力.用以模拟风载荷的推力通过安装于塔筒顶端的六分力仪测得,传感器具体安装位置与相关先前研究[16]一致.

图2 半潜式浮式风机试验模型
表1 平台各物理量相似比对照

Tab.1 Comparison among similarity ratios of physical parameters of platform
此外,浮式风力机平台用9根系泊缆绳进行系泊,每个立柱3根系泊绳.每根系泊缆绳由链接钩、弹簧以及锚链3部分组合而成.在试验中,由于水池尺寸较大,没有对系泊缆进行等效截断,而是对完整系泊缆进行了调试以满足长度以及系泊缆刚度的相似.系泊缆具体的布置以及刚度将在下一节中具体介绍.
1.3 白噪声非规则波试验

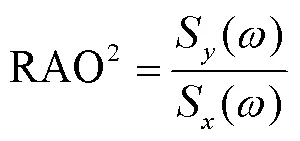
由于现实中的非规则波谱多为窄带谱,在低频和高频区间的波浪能量较小,引起的运动响应幅值较小,二者的比值计算得到的RAO误差则相对较大.因此,目前对浮体运动响应的研究的主流方法仍然是通过大规模规则波试验得到RAO,然而这种方法既费时又耗力[17].白噪声非规则波是一种理想化的非规则波浪谱,现实海洋环境中并不存在,其频谱在所研究的波浪频率范围内能量基本一致,因此理想情况下白噪声非规则波浪谱曲线应是平直的,白噪声试验分析所得的RAO在相当宽广的频率范围是正确可靠的[18].本文对平台运动响应的计算、验证以及后续有关风载荷对运动影响的研究均建立在白噪声非规则波试验基础之上.
2 数值模型建立及试验对比验证
本文中的数值计算在浮体运动响应计算部分所用方法为时域和频域的基于势流理论的边界元方法,并考虑二阶的波浪载荷的影响.系泊系统的计算则主要基于悬链线理论,利用动态分析方法充分考虑了系泊缆的动态效应[19].上述理论均是成熟且公认的理论方法,且本文所用计算软件属于成熟的商业势流边界元计算软件,方法理论不再赘述.
2.1 几何三维模型的建立
利用ANSYS Mechanical APDL对平台基础进行实尺度下的几何建模.坐标系定义如图3所示,其中坐标系原点竖直方向位置位于水线面处,风电机组迎风面朝向轴正轴,为右手坐标系,轴与塔筒中心线重合且正方向竖直向上,轴与图3中一根支架平行.平台质量特性参数见表2.

图3 平台全局坐标系的定义
表2 平台质量特性

Tab.2 Mass characteristics of platform
平台基础的几何建模如图4所示,其中平台垂荡阻尼板在几何模型中没有建出,这是由于垂荡阻尼板是厚度相对极薄的结构,在进行势流边界元计算时,通常用一种特殊的没有质量和厚度的莫里森单元来模拟其受到的水动力载荷[20].此外,几何模型不建出垂荡板,可避免过薄的几何形状导致画网格时需要局部加密增大工作量和网格量.
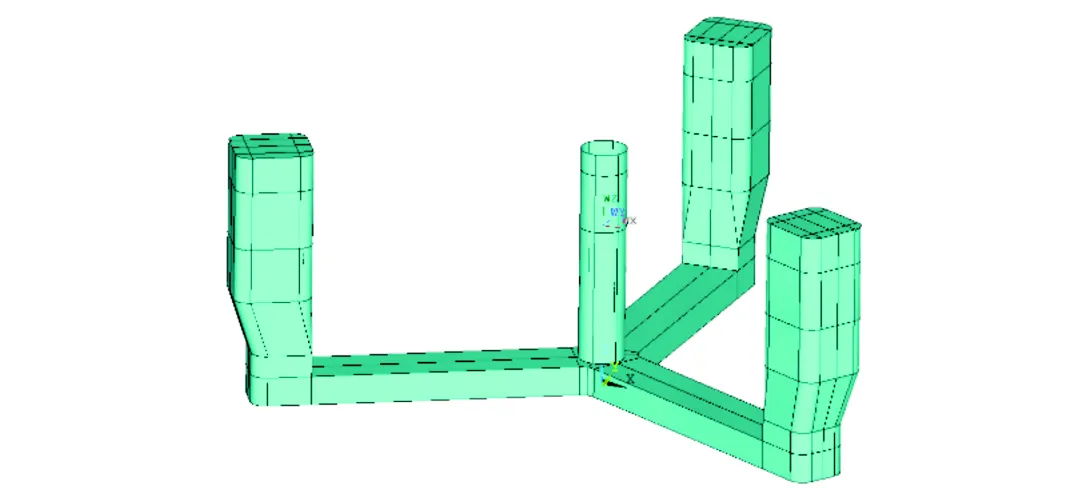
图4 平台几何三维模型
2.2 数值有限元模型的建立
建立数值有限元模型时,需要考虑平台基础的系泊系统,根据表3中系泊点坐标和表4中锚泊点坐标可定义出系泊缆(刚度见表5)的布置范围,如图5(a)所示,系泊点1~9分别位于平台3个立柱上,与之对应的锚泊点1~9布置于远端.
表3 平台系泊点坐标
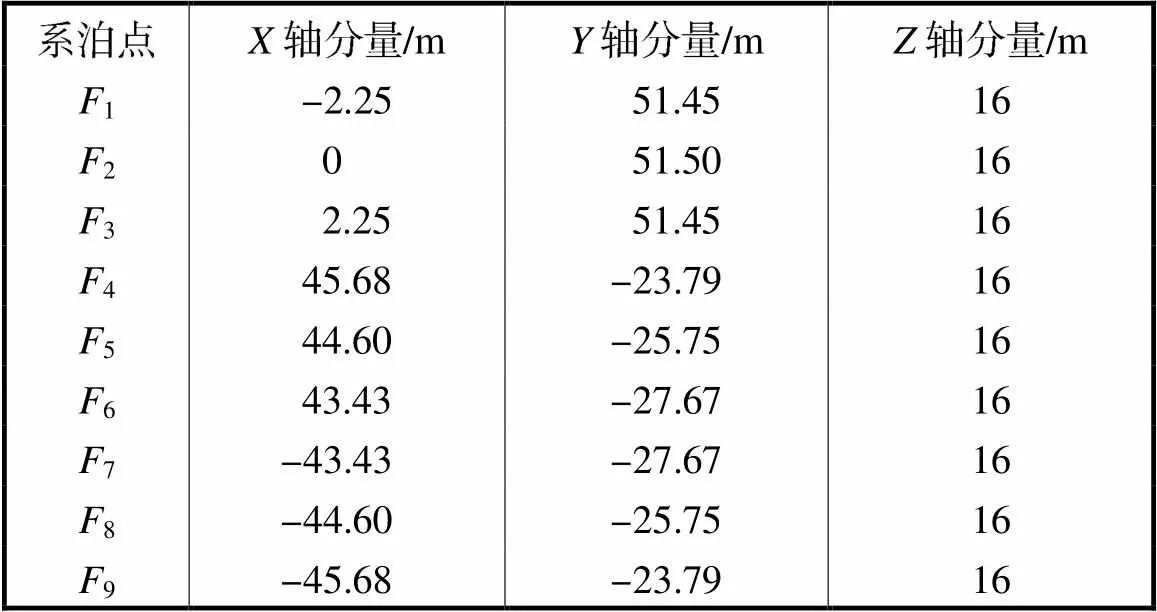
Tab.3 Coordinates of mooring points of platform
表4 平台锚泊点坐标
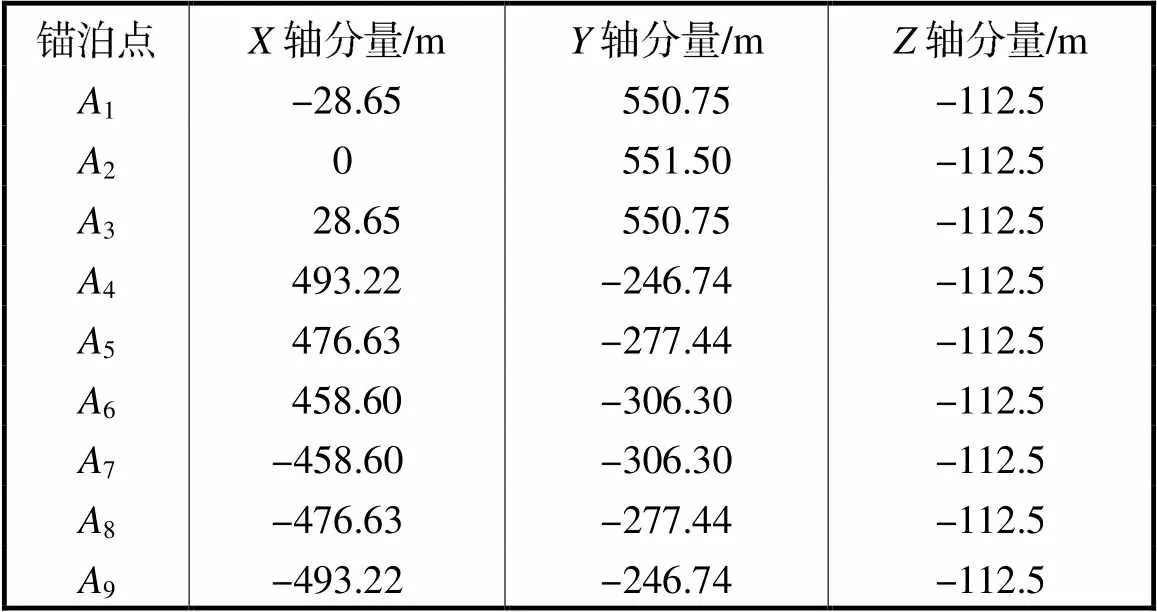
Tab.4 Coordinates of anchoring points of platform
表5 平台系泊缆刚度
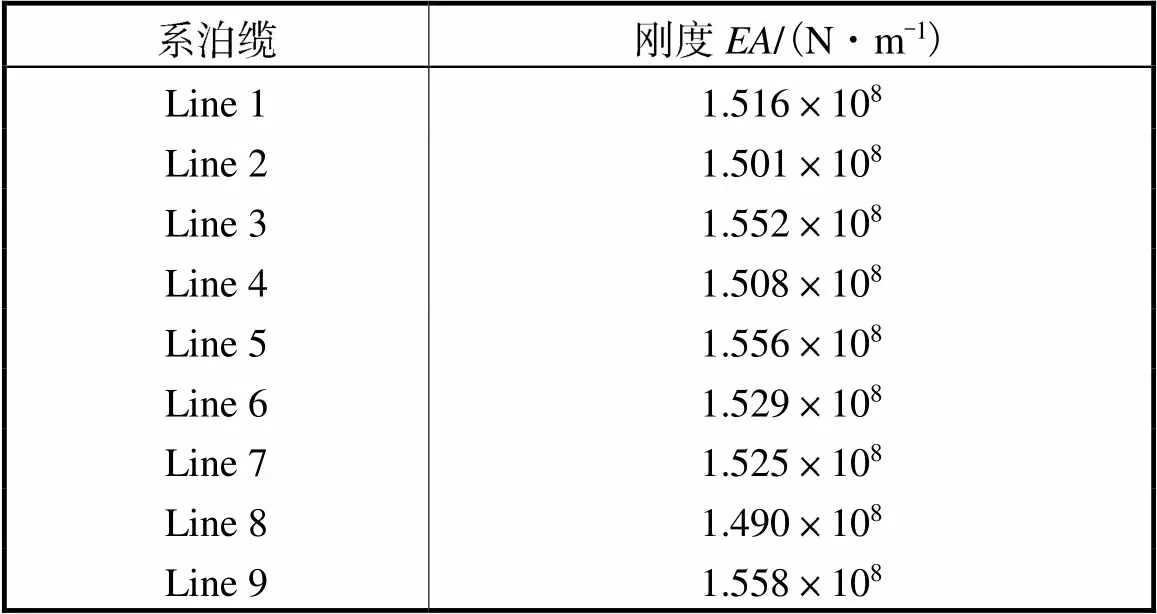
Tab.5 Stiffness of mooring lines of platform
最终建立系泊状态下的平台有限元模型如图5(b)所示,平台各立柱底部均有单独设置的无厚度的莫里森单元来模拟圆形垂荡板(如图5(c)所示).此外,注意到图5(b)中AQWA数值有限元模型的全局坐标系与之前一致,而随体坐标系原点则在重心处.
考虑到AQWA-Line计算时网格不能超过18000个,且1个波长范围内应不少于7个网格.在此基础上进行网格收敛性验证,网格尺寸为0.5m(粗)、1m(中)和2m(细)的3套网格划分策略计算得到的结果几乎完全吻合(见图6).
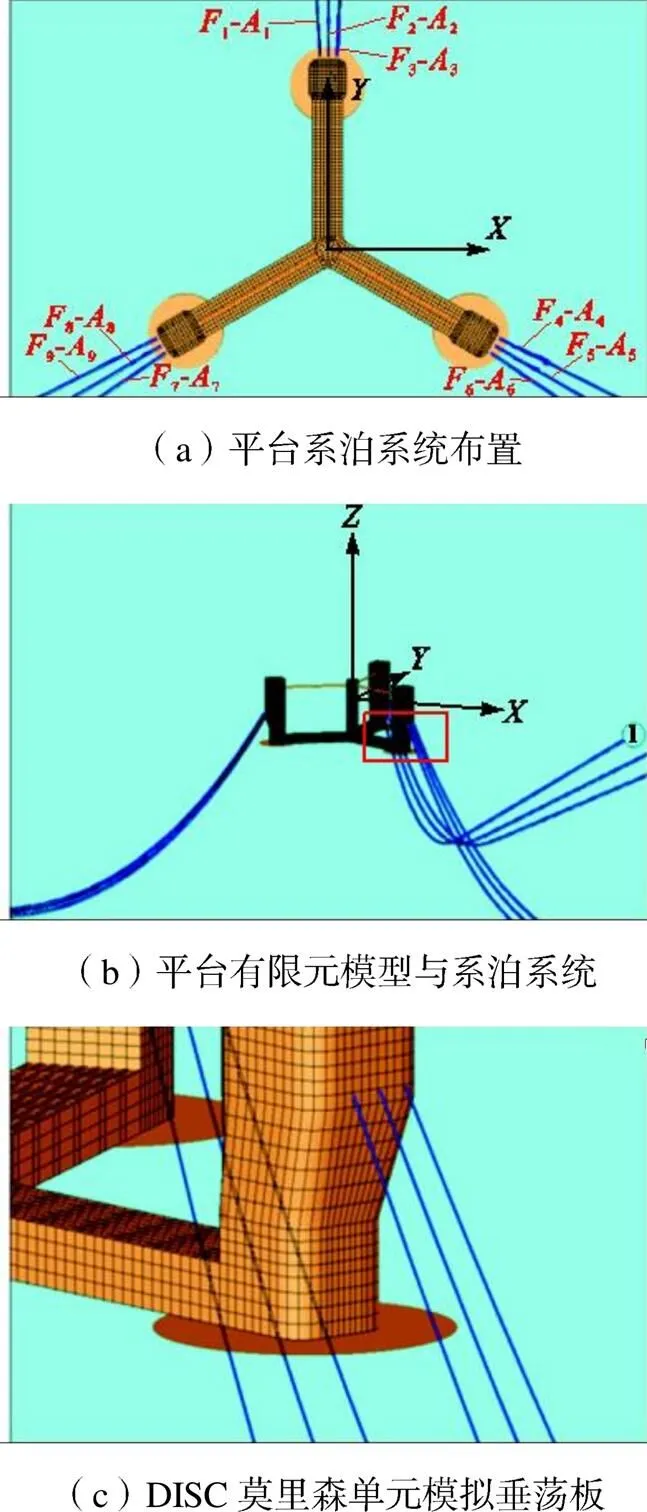
图5 平台有限元模型

图6 网格收敛性验证
网格敏感性分析见表6.由于上述用于验证网格收敛性的参考是RAO曲线,因此用拟合优度(也称决定系数)2来衡量曲线间误差[21],可以发现粗网格与中网格拟合优度可达0.9896,中网格与细网格间的拟合优度可达0.9934,这意味着中网格与细网格计算得到的结果间差异较中网格与粗网格间的差异更小,计算结果是随网格尺寸收敛的.因此最终采用中网格,即网格尺寸为1m的映射网格划分策略,网格总量为9888.
表6 网格敏感性分析

Tab.6 Sensitivity analysis of mesh
2.3 静水自由衰减试验及阻尼修正
势流边界元软件在计算时无法考虑水的黏性,水黏性引起的阻尼通常需要通过其他方法(如模型试验或者CFD)进行静水自由衰减试验,来辅助修正势流计算时需要考虑的阻尼.静水自由衰减试验在平静水面进行,通常给予模型相应自由度的初始位移,然后释放模型,使其在阻尼作用下做相应自由度的自由衰减运动.通过自由衰减运动的时程曲线(见图7)得到其消灭曲线(见图8),从而利用消灭曲线法[22]进行阻尼修正.
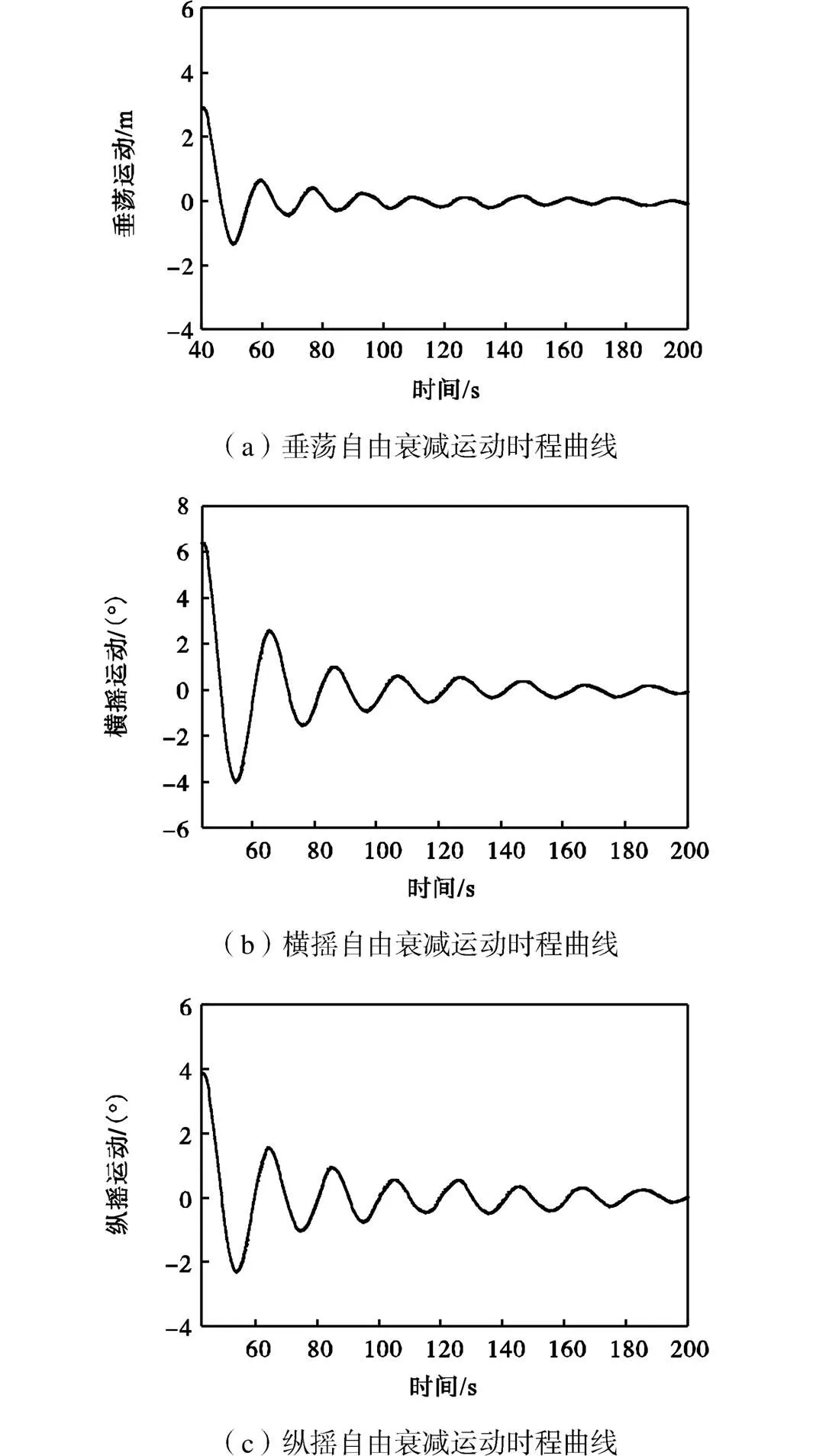
图7 垂荡、横摇和纵摇自由衰减运动时程曲线
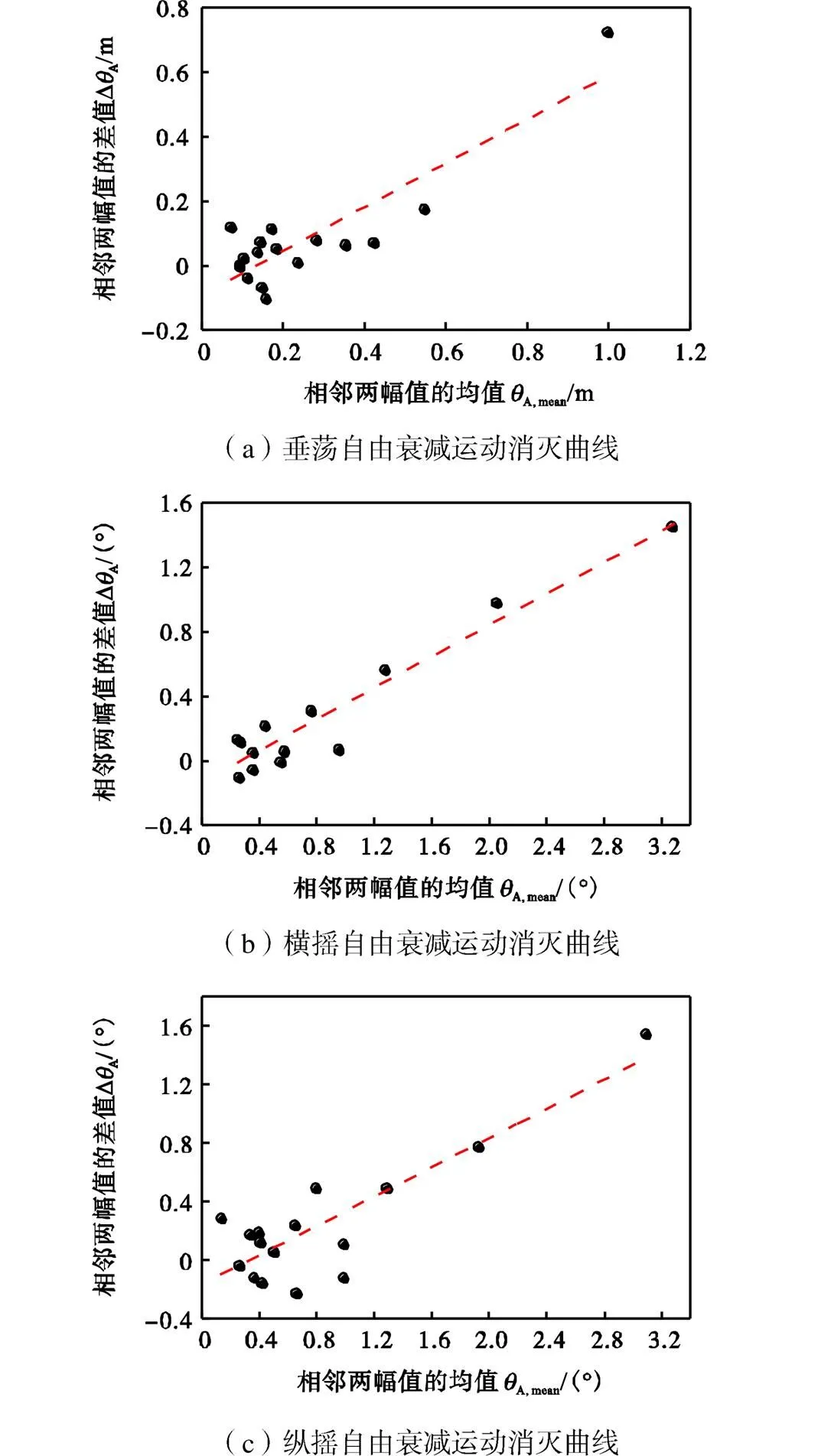
图8 垂荡、横摇和纵摇自由衰减运动消灭曲线
利用上述自由衰减试验得到消灭曲线,其斜率即自由衰减系数,根据式(2)和(3)可以计算得到无因次的自由衰减系数和阻尼修正值为
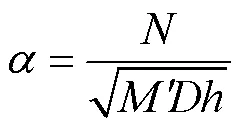
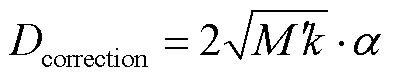
根据上述自由衰减运动的时程曲线的振荡周期可以得到垂荡、横摇和纵摇的固有周期或固有频率,详见表7.再根据上述阻尼修正方法,利用固有周期结果进行计算,即可得到需要修正的阻尼值.阻尼修正计算具体结果见表8.
表7 固有周期和固有频率
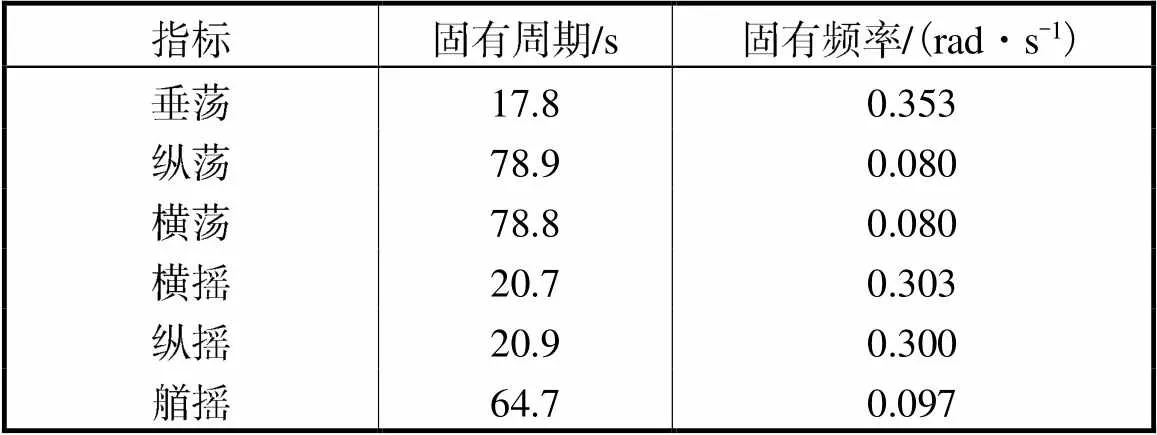
Tab.7 Natural period and natural frequency
表8 阻尼修正
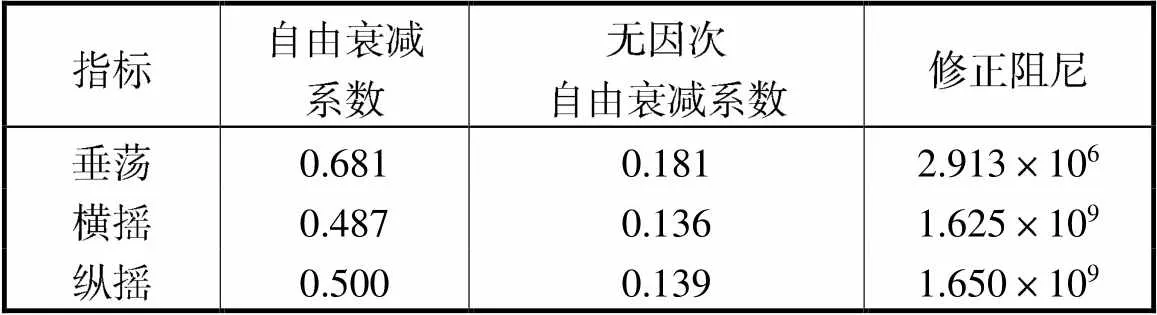
Tab.8 Damping correction
2.4 阻尼修正后运动RAO对比验证
修正阻尼值后利用势流边界元频域数值方法可计算得到平台基础运动RAO,计算结果与模型试验测得结果进行对比分析可以验证数值算法的准确性与可行性.本节对180°浪向(轴正向为迎浪方向)下的平台基础6自由度运动RAO对比分析.其中模型试验结果是根据运动时程曲线进行时频域转换得到运动响应谱后与入射海浪谱进行对比(即根据式(1))得到.对比结果如图9所示.
对比图9中试验与数值结果可以发现:数值结果与模型试验结果吻合良好,在高频段(波浪频率>1.2rad/s)存在一定误差,这是因为白噪声非规则波只有在理想情况下才在各个波浪频率处的能量相同.实际情况下,试验产生的白噪声非规则波通常在低频(波浪频率<0.25rad/s)和高频处能量极小.根据式(1)相除时误差会被放大.图10中的白噪声非规则波的能量谱可以验证上述观点.
此外,纵荡、垂荡、纵摇和艏摇运动响应RAO均有较明显的双峰特征,第1个峰值频率出现在各自由度的运动固有频率附近(固有频率参考表7,其中值得注意的是艏摇固有频率约为0.097rad/s,超过了计算和试验数据处理范围,因此固有频率处第1个峰值未显现).通过对比数值计算得到的这4个自由度的波浪激励力(入射波浪载荷加上绕射波浪载荷),发现第2个峰值主要由波浪激励力引起,如图11所示.
可以发现纵荡、垂荡、纵摇和艏摇运动RAO的双峰特征中的第2个峰值对应的波频与波浪激励力极大值所对应波频基本吻合:纵荡第2个峰值与纵荡波浪激励力极值频率均在1.25rad/s附近;垂荡在0.7rad/s附近;纵摇在0.8rad/s附近;艏摇较为特殊,由于其固有频率(约0.097rad/s)处峰值无法显现,艏摇运动RAO的双峰均受波浪激励力影响,对应0.9rad/s以及1.5rad/s频率附近.
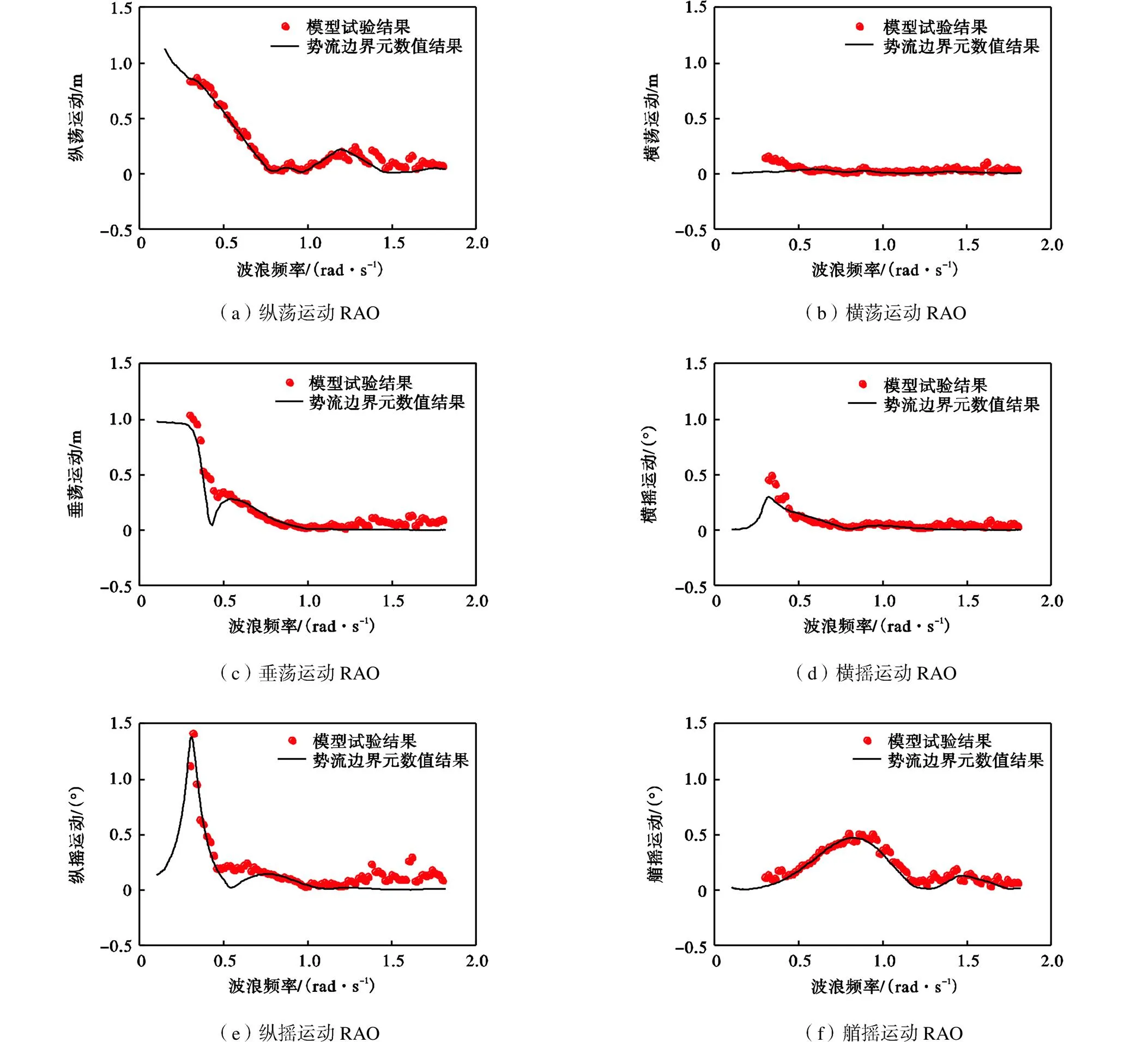
图9 180°白噪声非规则波作用下6自由度运动RAO
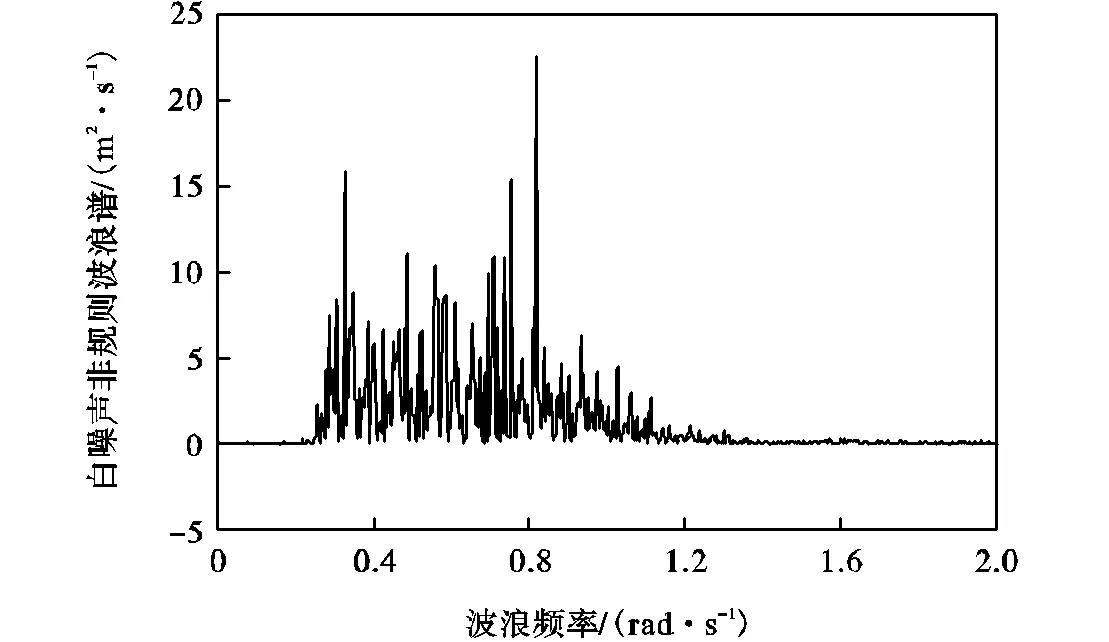
图10 180°白噪声非规则波浪谱

图11 纵荡、垂荡、纵摇和艏摇激励力RAO
3 风载荷对运动响应的影响
3.1 模型试验中定常风载荷对运动响应的影响
分别对比无风与在定常风载荷(风向与浪向一致)作用下的白噪声非规则波模型试验得到的平台运动响应,来讨论风载荷对运动响应的影响.
如图12所示,通过对比有风和无风条件下模型试验得到的平台运动RAO曲线,可以发现定常风对平台在纵、横、垂荡及横摇(图12(a)~(d))和艏摇(图12(f))方向的影响相当有限,对纵摇则存在较为显著的影响.进一步对比有风和无风条件下的纵摇运动响应(图12(e)),可以发现在纵摇固有频率(波浪频率=0.3rad/s)处存在较大差异;风载荷作用使得平台在固有频率处的纵摇运动响应幅值减小了近22%.由于白噪声谱在低频和高频处能量较小,数据处理误差不可控,因此在各图中已进行频率范围截断.
3.2 数值方法探究风载荷对平台运动影响的机制
3.2.1 考虑风、浪载荷共同作用的数值方法的验证
由上节内容可以发现,在180°风浪联合作用下,受风载荷影响最大的纵摇方向的运动并未在风的作用下进一步增大运动响应,反而显著减小了约22%.考虑到此时波浪与风都是非规则时域信号,若此时波浪载荷与风载荷峰值频率接近且在峰值频率处波浪载荷与风载荷处于接近的量级水平,但是作用相位相反,则引起纵摇的外部载荷将相互抵消削弱,从而造成上述结果.为进一步探究风载荷对平台运动产生此类影响的原因,需要分别得到平台所受的风载荷和波浪载荷.风载荷的时域信号已经在试验中测得,波浪载荷则缺少相应的试验数据,因此可通过数值方法获得波浪载荷数据.
基于势流边界元理论的频域数值方法在第2.3节中已得到验证,在此基础上对时域数值方法进行验证.由于主要讨论纵摇方向的影响,因此后续验证将以该自由度为主.时域数值方法计算流程如图13所示,将有风条件下的白噪声非规则波试验测得的波面升高(图14(a))与风载荷(图14(b))时域数据作为时域数值算法的输入参数来计算风浪载荷下平台基础的纵摇运动响应,计算得到的纵摇时域运动信号如图14(c)所示,可见风载荷改变了平台的纵摇平衡位置(风载荷作用下纵摇平衡位置约在-1.5°而非0°处).
对上述时域数值方法得到的有风条件下平台纵摇时域信号进行处理可以得到平台纵摇运动RAO,如图14(d)所示.与有风条件下试验方法得到的纵摇运动RAO对比,可以发现时域数值结果的大小及变化趋势能与试验结果较好吻合.此外,与无风条件下频域数值方法/试验方法得到的纵摇RAO相比,同样可以发现风载荷减小了平台在纵摇固有频率处的纵摇运动幅度,与第3.1节中结果相印证.
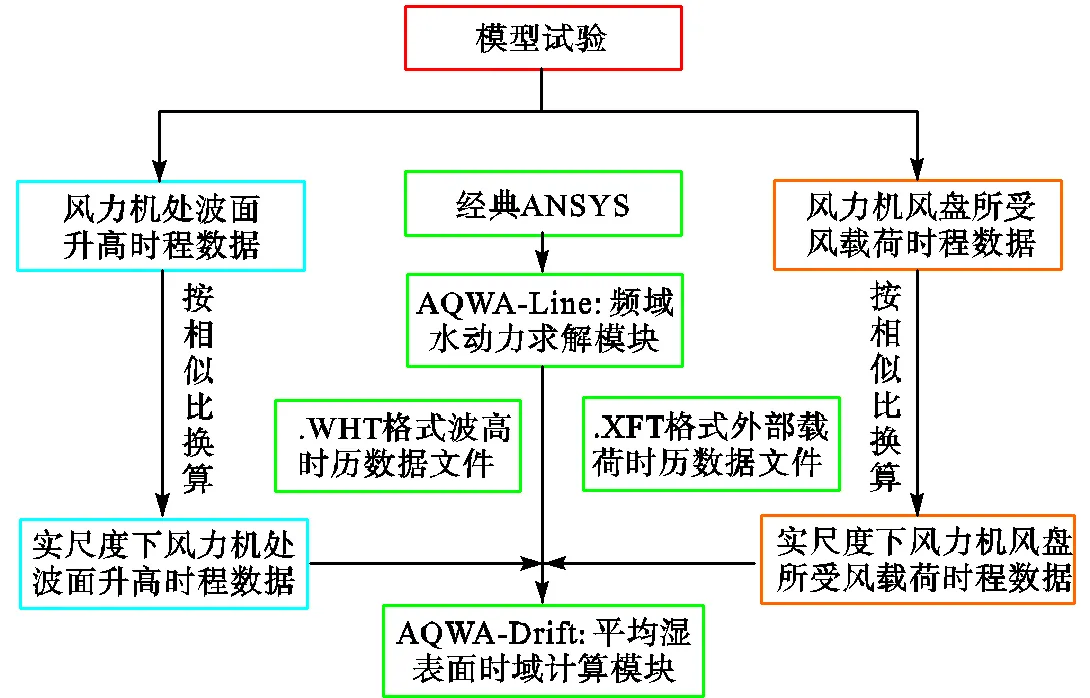
图13 考虑风、浪载荷的时域数值方法计算流程
3.2.2 波浪载荷的计算
通过上述方法对势流边界元时域数值方法的计算结果可靠性与准确性进行了验证.考虑到需要验证风载荷使平台纵摇运动幅度减小的原因是风载荷与波浪载荷量级相当而相位相反,且风载荷在试验中已经测得,因此仍需要波浪载荷的时域信号.
通过上述时域分析方法可以计算得到平台受到的波浪载荷时域信号(图15),其量级与平台风力机机组引起的基础平台所受风载荷(图14(b))量级 相当.
3.2.3 载荷信号的时频转换及风、浪载荷的相位差
对上述波浪载荷(图15)与风载荷(图14(b))的时域信号数据进行快速傅里叶变换,可以分别得到波浪载荷(图16(a))与风载荷(图16(b))的幅值频谱.
由图16可发现,风载荷与波浪载荷均在平台纵摇固有频率(=0.3rad/s)处存在较大的峰值,且峰值的数量级基本相当,此时平台所受的总载荷同时受到风载荷与波浪载荷支配.这意味着当平台的纵摇频率在0.3rad/s时,由于风载荷能量集中频率也在该频率处,若此时风载荷与波浪载荷作用相位相反,则极可能导致载荷相互抵消,进而减小纵摇运动幅度.因此,需要进一步计算波浪载荷与风载荷相位谱,并对其相位差的频谱加以验证.
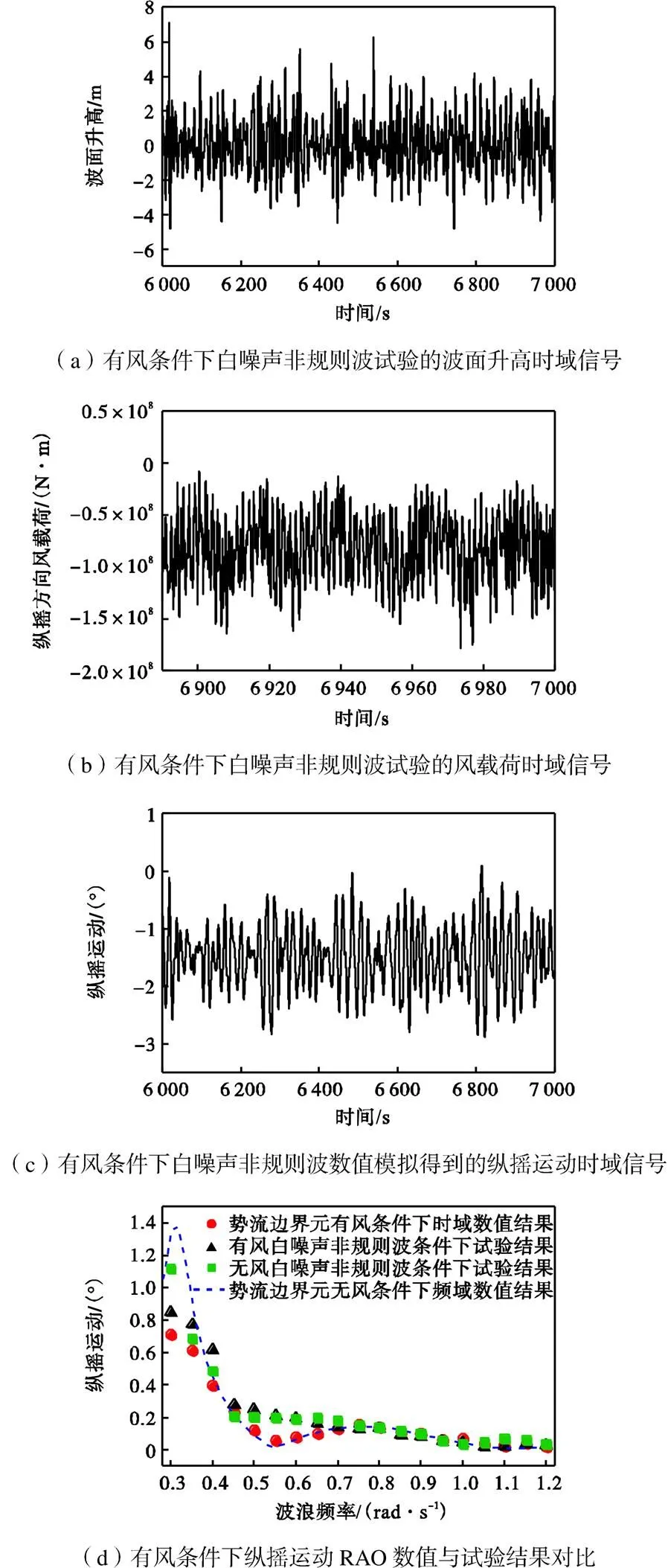
图14 有风条件下纵摇运动RAO的数值求解方法的验证
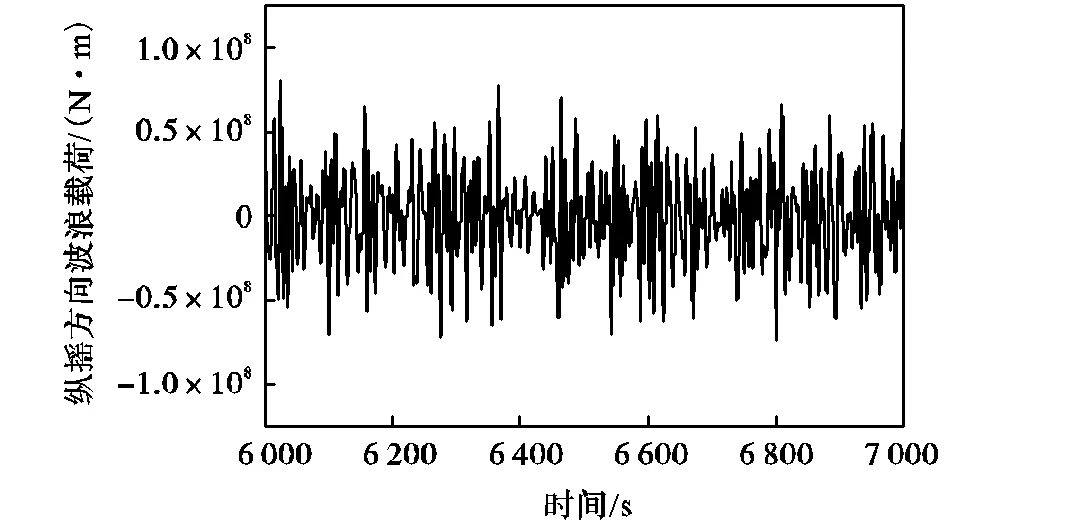
图15 纵摇方向波浪载荷时域信号

图16 纵摇方向波浪、风载荷幅值频谱

综上,波浪载荷与风载荷的主要频率成分同频(同为约0.3rad/s频率),且刚好位于平台纵摇运动共振频率处.与此同时,波浪载荷与风载荷的作用相位刚好相反是造成此时在风、浪载荷共同作用下,平台纵摇运动幅度被显著削弱的主要原因.
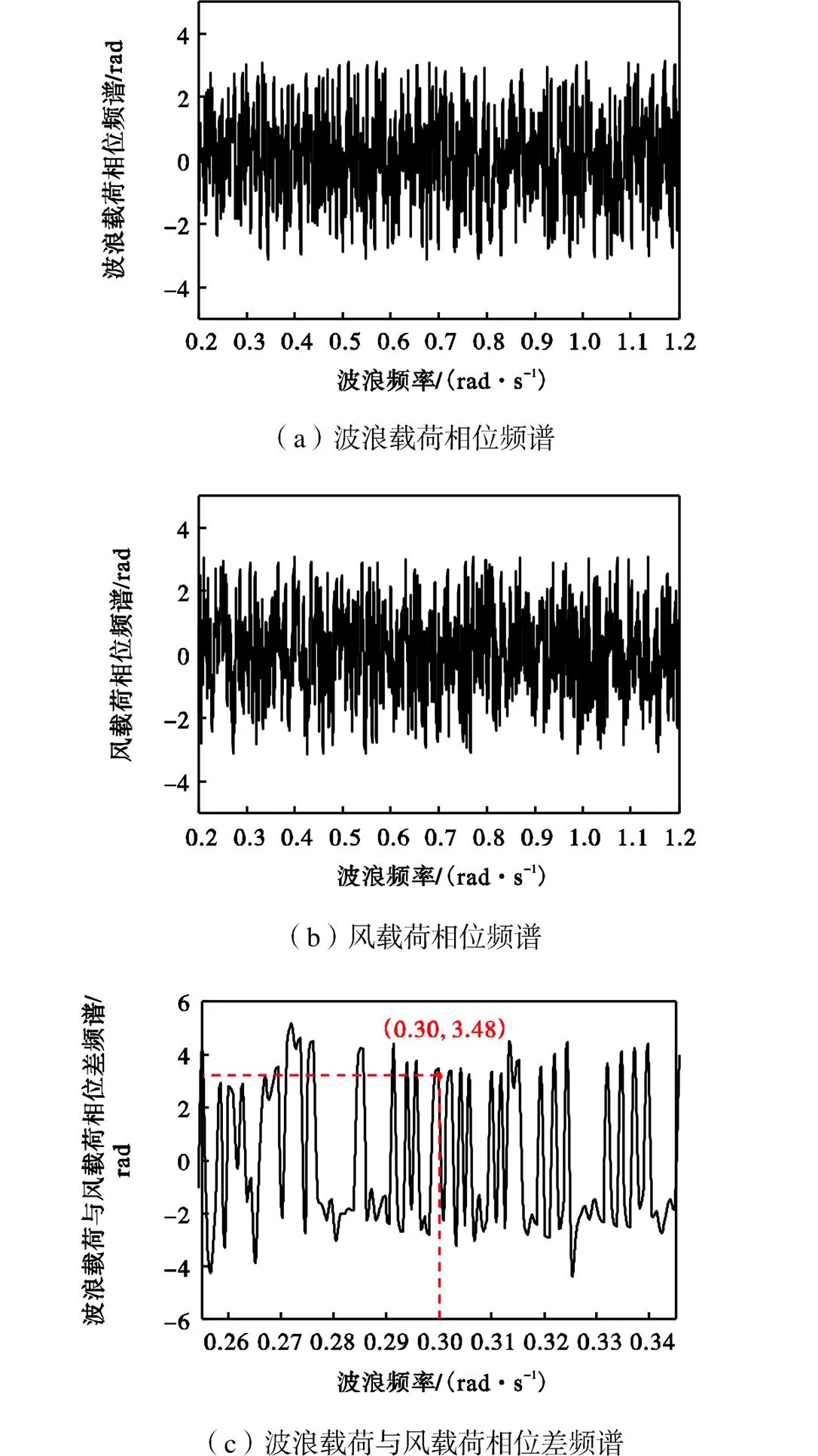
图17 纵摇方向波浪载荷与风载荷相位谱与相位差频谱
4 结 论
本文对某型6MW浮式风电机组的水池试验数据进行了处理,并与数值结果进行对比验证确保处理方法的准确性,通过对比有风条件下和无风条件下的白噪声非规则波试验数据处理结果发现风载荷对平台运动存在影响.最终通过考虑风浪共同作用的势流边界元的时域数值方法对此进行深入研究,探讨风载荷的影响机制.
(1) 利用白噪声非规则波试验求得的浮体运动RAO在广泛的波浪频率范围内是准确的,能与势流边界元方法求得的运动RAO较好吻合,而白噪声非规则波谱能量较小处求得的运动响应则误差不可控.
(2) 定常风的风载荷作用下,风载荷对平台运动存在一定的影响,这种影响主要集中在风载荷作用最显著的运动自由度上,且这种影响的形式及程度与风、浪载荷主要频率成分处频率、幅值以及相位有关.
(3) 当风、浪载荷的主要频率成分同频且位于平台运动固有频率处时,风载荷的影响能够显著体现,此时若风、浪载荷同相位,则联合载荷作用下相关自由度的运动幅值将显著增大.反之,则显著减小,这也是本文研究中风载荷削弱了平台运动响应这一现象的根本原因.
[1]董霄峰,练继建,王海军. 海上风机结构振动监测试验与特性分析[J]. 天津大学学报(自然科学与工程技术版),2019,52(2):191-199.
Dong Xiaofeng,Lian Jijian,Wang Haijun. Monitoring experiment and characteristic analysis of structural vibration of offshore wind turbine[J]. Journal of Tianjin University(Science and Technology),2019,52(2):191-199(in Chinese).
[2]Gao Z T,Feng X Y,Zhang Z T,et al. A brief discussion on offshore wind turbine hydrodynamics problem[J]. Journal of Hydrodynamics,2022,34(1):15-30.
[3]Heronemus W E. Pollution-free energy from offshore winds[C]//8th Annual Conference and Exposition,Marine Technology Society. Washington DC,USA,1972.
[4]Jonkman J M. Loads Analysis of a Floating Offshore Wind Turbine Using Fully Coupled Simulation[R]. Golden,USA:National Renewable Energy Lab,2007.
[5]Jonkman J M,Matha D. Dynamics of offshore floating wind turbines—Analysis of three concepts[J]. Wind Energy,2011,14(4):557-569.
[6]Kvittem M I,Bachynski E E,Moan T. Effects of hydrodynamic modelling in fully coupled simulations of a semi-submersible wind turbine[J]. Energy Procedia,2012,24:351-362.
[7]Meng L,Zhou T,He Y,et al. Concept design and coupled dynamic response analysis on 6-MW spar-type floating offshore wind turbine[J]. China Ocean Engineering,2017,31(5):567-577.
[8]Goupee A J,Koo B J,Kimball R W,et al. Experimental comparison of three floating wind turbine concepts[J]. Journal of Offshore Mechanics and Arctic Engineering,2014,136(2):020906.
[9]Kimball R,Goupee A J,Fowler M J,et al. Wind/wave basin verification of a performance-matched scale-model wind turbine on a floating offshore wind turbine platform[C]//International Conference on Offshore Mechanics and Arctic Engineering. San Francisco,USA:American Society of Mechanical Engineers,2014.
[10]Zhang L,Li Y,Xu W,et al. Systematic analysis of performance and cost of two floating offshore wind turbines with significant interactions[J]. Applied Energy,2022,321:119341.
[11]马 钰. 单柱式浮式风机动力性能机理研究[D]. 上海:上海交通大学船舶海洋与建筑工程学院,2014.
Ma Yu. Research on Dynamic Analysis for a Spar Type Offshore Floating Wind Turbine[D]. Shanghai:School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,2014(in Chinese).
[12]张靖晨,李 焱,唐友刚,等. 新型浅吃水浮式基础风力机动力响应研究[J]. 太阳能学报,2021,42(7):378-383.
Zhang Jingchen,Li Yan,Tang Yougang,et al. Analysis on dynamic response of new type reduced draft floating foundation wind turbine[J]. Acta Energiae Solaris Sinica,2021,42(7):378-383(in Chinese).
[13]阳 杰,何炎平,孟 龙,等. 极限海况下6MW 单柱型浮式风力机耦合动力响应[J]. 上海交通大学学报,2021,55(1):21-31.
Yang Jie,He Yanping,Meng Long,et al. Coupled dynamic response on a 6MW spar-type floating offshore wind turbine under extreme conditions[J]. Journal of Shanghai Jiao Tong University,2021,55(1):21-31(in Chinese).
[14]Shah K A,Meng F,Li Y,et al. A synthesis of feasible control methods for floating offshore wind turbine system dynamics[J]. Renewable and Sustainable Energy Reviews,2021,151:111525.
[15]刘晓辉,高人杰,薛 宇. 浮式风力发电机组现状及发展趋势综述[J]. 分布式能源,2020,5(3):39-46.
Liu Xiaohui,Gao Renjie,Xue Yu. Current situation and future development trend of floating offshore wind turbine[J]. Distributed Energy,2020,5(3):39-46(in Chinese).
[16]李荣富,方 龙,宁巧珍,等. 半潜式与固定式海上风力机气动性能水池模型试验对比研究[J]. 可再生能源,2022,40(7):914-920.
Li Rongfu,Fang Long,Ning Qiaozhen,et al. A comparative experimental study on floating and fixed bottomoffshore wind turbines[J]. Renewable Energy Re-sources,2022,40(7):914-920(in Chinese).
[17]李宏伟,庞永杰,孙 哲,等. 白噪声不规则波与聚焦波的水池模拟[J]. 华中科技大学学报(自然科学版),2013,41(1):89-92.
Li Hongwei,Pang Yongjie,Sun Zhe,et al. Simulation of white noise irregular wave and focused wave in ocean basin[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2013,41(1):89-92(in Chinese).
[18]杨建民,肖龙飞,盛振邦. 海洋工程水动力学试验研究[M]. 上海:上海交通大学出版社,2008.
Yang Jianmin,Xiao Longfei,Sheng Zhenbang. Experimental Study of Hydrodynamics in Ocean Engineering[M]. Shanghai:Shanghai Jiao Tong University Press,2008(in Chinese).
[19]冷述栋. CALM系泊系统动力响应分析[D]. 大连:大连理工大学船舶工程学院,2013.
Leng Shudong. Dynamic Response Analysis of CALM Mooring System[D]. Dalian:School of Naval Architecture and Ocean Engineering,Dalian University of Technology,2013(in Chinese).
[20]高 巍,董 璐,黄 晶. ANSYS AQWA软件入门与提高[M]. 北京:中国水利水电出版社,2018.
Gao Wei,Dong Lu,Huang Jing. Getting Started and Improving of the Software of ANSYS AQWA[M]. Beijing:China Water & Power Press,2018(in Chinese).
[21]Di Bucchianico Alessandro. Coefficient of determina-tion(2)[M]//Encyclopedia of Statistics in Quality and Reliability. Wiley,2008.
[22]Faltinsen O. Sea Loads on Ships and Offshore Structures [M]. Cambridge,UK:Cambridge University Press,1993.
Hydrodynamic Model Test and Numerical Simulation of Semi-Submersible Wind Turbine Platform
Fang Long1, 2,Zhai Endi2,Li Rongfu2,Zhao Zihan3,Shao Changsheng3,Zhang Lijun4, 5
(1. School of Civil Engineering,Tianjin University,Tianjin 300072,China;2. Beijing Goldwind Science & Creation Windpower Equipment Co.,Ltd.,Beijing 100176,China;3. Southern Marine Science and Engineering Guangdong Laboratory(Zhanjiang),Zhanjiang 524002,China;4. School of Naval Architecture,Ocean & Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;5. Donghai Laboratory,Zhoushan 316021,China)
Aimed at the influence of wind load on the foundation’s motion response of one floating wind turbine in deep sea,the wave tank model test of a scale model and the numerical calculations of a full-scale model were carried out. According to the free-decay curves and extinction curves obtained from the free-decay experiment conducted in the wave tank,the necessary damping correction was performed on the numerical model established based on the potential flow boundary element method. The platform’s motion RAOs calculated by the numerical method were compared with the platform’s motion response results measured in the wave tank model test,where the white noise irregular wave was generated,thus ensuring the accuracy of the established numerical model. At the same time,the feasibility of the white noise irregular wave experiment was also verified. Through the combination of the time- and frequency-domain numerical calculation methods and experimental methods,the motion responses of the platform under the action of white noise irregular wave with constant wind or with no wind,as well as the amplitude and phase spectra of related wave and wind loads,were compared and studied. According to the above calculation and research results,the main influencing forms of wind load for the floating foundation’s motion response of the semi-submersible wind turbine and the corresponding reasons were preliminarily summarized. Results show that the influence of wind load on the platform’s motion is related to the frequency,amplitude and phase of the main frequency components of wind and wave loads. When the energy concentration frequencies of wind and wave loads basically agree with each other and they also overlap with the natural frequency of the platform’s motion,the influence of wind load will be significantly reflected (with a difference of about 22% in this paper). As to the form of influence (e.g., enhancing or weakening the motion amplitude),it depends on the phase difference between the wind and wave loads at the time. When the wind and wave loads are in the same phase,the motion amplitude of relevant degrees of freedom under the combined loads will increase significantly. In contrary,the motion amplitude will decrease significantly when the two loads are different in terms of phase.
floating offshore wind turbine;motion response;aerodynamic load;model test;numerical simulation;potential flow boundary element
10.11784/tdxbz202301010
TK83
A
0493-2137(2023)11-1145-12
2023-01-09;
2023-03-15.
方 龙(1988— ),男,博士研究生,工程师,fanglong@goldwind.com.Email:m_bigm@tju.edu.cn
赵子晗,hans_zhao@zjblab.com.
国家重点基础研究发展计划资助项目(2019YFE0102500);东海实验室基金资助项目(DH-2022KF0304).
the National Basic Research Program of China(No.2019YFE0102500),the Science Foundation of Donghai Laboratory (No.DH-2022KF0304).
(责任编辑:武立有)
