基于分层强化学习的无人机机动决策*

杨晟琦，田明俊，司迎利，金琳乘

（1.中国航空工业集团公司沈阳飞机设计研究所，沈阳 110035；2.中国空空导弹研究院，河南 洛阳 471009）

0 引言

现代空战对高动态和强实时的需求逐渐增长，人类飞行员的决策受限于反应速度和环境适应性。而人工智能由于不存在人类飞行员的相关局限性而逐渐展现优势［1］。因此，无人机的机动决策成为航空科学中一个越来越重要的研究领域。微分对策、人工势场、模糊推理、遗传算法等算法均被用于解决无人机的机动决策问题［2-6］。此外，以深度强化学习（deep reinforcement learning，DRL）为代表的人工智能技术与此领域的交叉融合也得到了广泛研究［7-10］。其中，基于遗传模糊树开发的ALPHA 空战系统首次证明了基于人工智能技术的空战决策方法具有击败人类飞行员的潜力。然而，目前已有的方法均采用固定的决策间隔，这使得无人机的机动决策难以适应高动态和强实时的环境。

综上所述，本文采用分层强化学习（hierarchical reinforcement learning，HRL）方法，通过无人机在环境中的自我对弈，使无人机具备能够自适应调整决策间隔的自主机动决策能力，解决了无人机在高动态、强实时环境下的决策难题。

1 空战状态表征

本文将空战状态分为无人机绝对状态sa，相对状态sγ和本机导弹状态sm。绝对状态由以下元素构成：真空速v，当前高度h，爬升率h˙，速度倾角θ，速度偏角φ，法向过载nn，火控雷达锁定信号flock，电子告警信号fwarn，剩余空空导弹数量mleft。相对状态由以下元素构成：距离r，接近率r˙，相对高差Δh，目标进入角AA（目标速度矢量与视线矢量的夹角），本机雷达波束角AO（本机机头朝向与视线矢量的夹角）。导弹状态由以下元素构成：导弹速度vm，当前高度hm，导弹与目标距离rm，导弹与目标接近率r˙m，剩余命中时间tgo，导弹与目标之间的进入角AAm和波束角AOm。对于某个无人机，其整体的空战状态定义如下：

2 无人机机动模型

2.1 无人机运动学模型

为了便于研究无人机的机动决策，将无人机视为质点，则无人机的质点运动学方程为

式中，x，y，z 为无人机在惯性坐标系中的位置；x˙，y˙，z˙为无人机在惯性坐标系中的速度分量；θ 为无人机的速度倾角（速度矢量与水平面的夹角）；φ 为无人机的速度偏角（速度在水平面的投影与x 轴的夹角）；nx为速度方向的过载，nz为法向过载，φ 为绕速度矢量的滚转角；g 为重力加速度。

2.2 机动动作库

本文采用文献［11］中的扩展机动动作库，如图1 所示，将无人机在水平面的机动动作分为直线飞行，左转60 °，左转90 °，右转60 °，右转90 °共5种。无人机在垂直面的机动动作包含水平飞行，爬升30°，爬升60°，俯冲30°，俯冲60°共5 种。每个方向上的机动动作还包含加速、匀速、减速3 种状态。

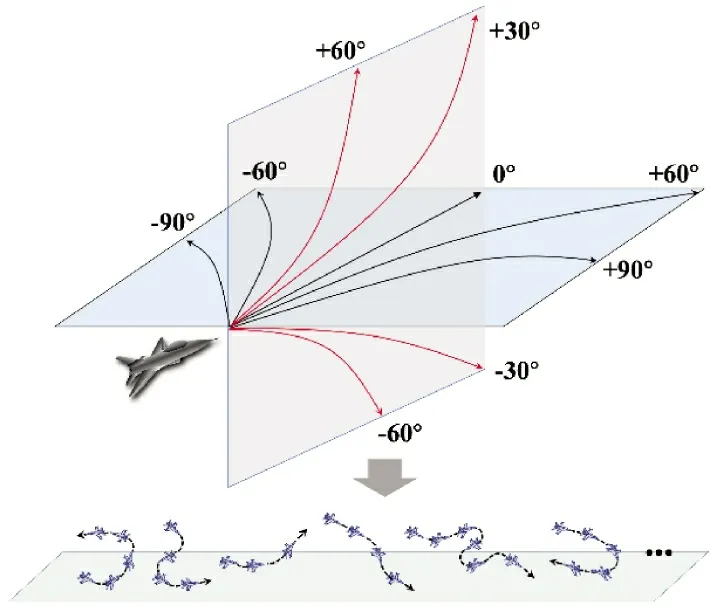
图1 机动动作库示意图Fig.1 Schematic diagram of maneuver action database

3 基于分层强化学习的无人机机动决策

为了自适应地调整决策间隔，提出机动选择策略和机动中断策略。无人机根据当前空战状态，依据机动选择策略选择具体实施的机动动作。在决策过程中，依据机动中断策略判断是否需要中断当前机动动作。本文基于Actor-Critic 的强化学习训练架构，构建机动选择策略网络、机动中断策略网络和价值网络。

3.1 策略和价值网络优化

将机动选择策略网络表示为πα，参数为α。将机动中断策略网络表示为πβ，参数为β。无人机选择一个机动动作执行直到πβ输出中断信号，然后根据πα输出新的动作a。策略πβ表示了动作的中断概率。为了防止无人机始终保持相同的动作，设置动作最大保持间隔为tmax。将最大化无人机获得的累积回报作为优化的目标函数。将无人机初始状态表示为s0，则无人机整体轨迹的期望累积回报可以表示为：

式中，γ∈（0，1）为折扣因子，rt为t 时刻获得的即时奖励。基于上述目标函数，状态价值函数可以表示为：

式中，Qπ为状态价值函数：

式中，p 为状态转移概率；U 为执行动作a 后状态转移至st+1后的价值，可以表示为：

无人机连续维持k 步动作不变的概率可以表示为：

当动作保持k 步后出现动作中断时，此时的状态转移概率为：

根据概率的链式法则，当上述的机动决策序列发生n 次时，整个决策过程的状态转移概率为：

综上，根据策略梯度定理，可以推导出机动选择策略网络和机动中断策略网络的参数更新方法。对于具有参数α 的机动选择策略网络πα，无人机期望累积回报对参数α 的梯度可以表示为：

根据动作中断策略网络参数的更新方式可知，当动作为最优时，优势函数为正，参数的梯度呈减小的趋势，从而减小动作中断的概率，使无人机继续保持当前的最优决策。反之，负的优势函数使动作中断概率增加，使无人机趋向于决策出更优的机动动作。通过动作的保持和中断，无人机能够自适应地调整决策间隔以在恰当时机作出准确的决策。

设价值网络参数为λ，则无人机期望累积回报对参数λ 的梯度可以表示为：

3.2 分层网络结构

为了使无人机学习机动策略，构建一个分层网络。整个网络将空战状态作为输入，输出当前选择的机动动作am，动作是否中断操作at和导弹射击指令as。空战状态通过全连接神经网络生成嵌入向量，将其拼接在一起生成包含全局信息的隐变量etot。进而通过softmax 函数，输出机动动作和射击指令的离散决策量。

在实际空战中，飞行员往往先根据态势选择合理的机动动作，然后根据实际情况判断是否继续执行此机动动作或调整为其他战术策略。因此，机动中断网络采用两级的分层决策结构来模仿这种决策顺序。将机动选择网络输出的机动动作和射击指令转换为one-hot 编码，并将其作为先验知识与隐变量etot共同生成动作是否中断操作at。

图2 展示了该分层网络的整体形式和输入输出关系。下页表1 具体说明了分层网络的结构。神经网络参数采用均值为0，方差为1 的正态分布进行随机初始化。

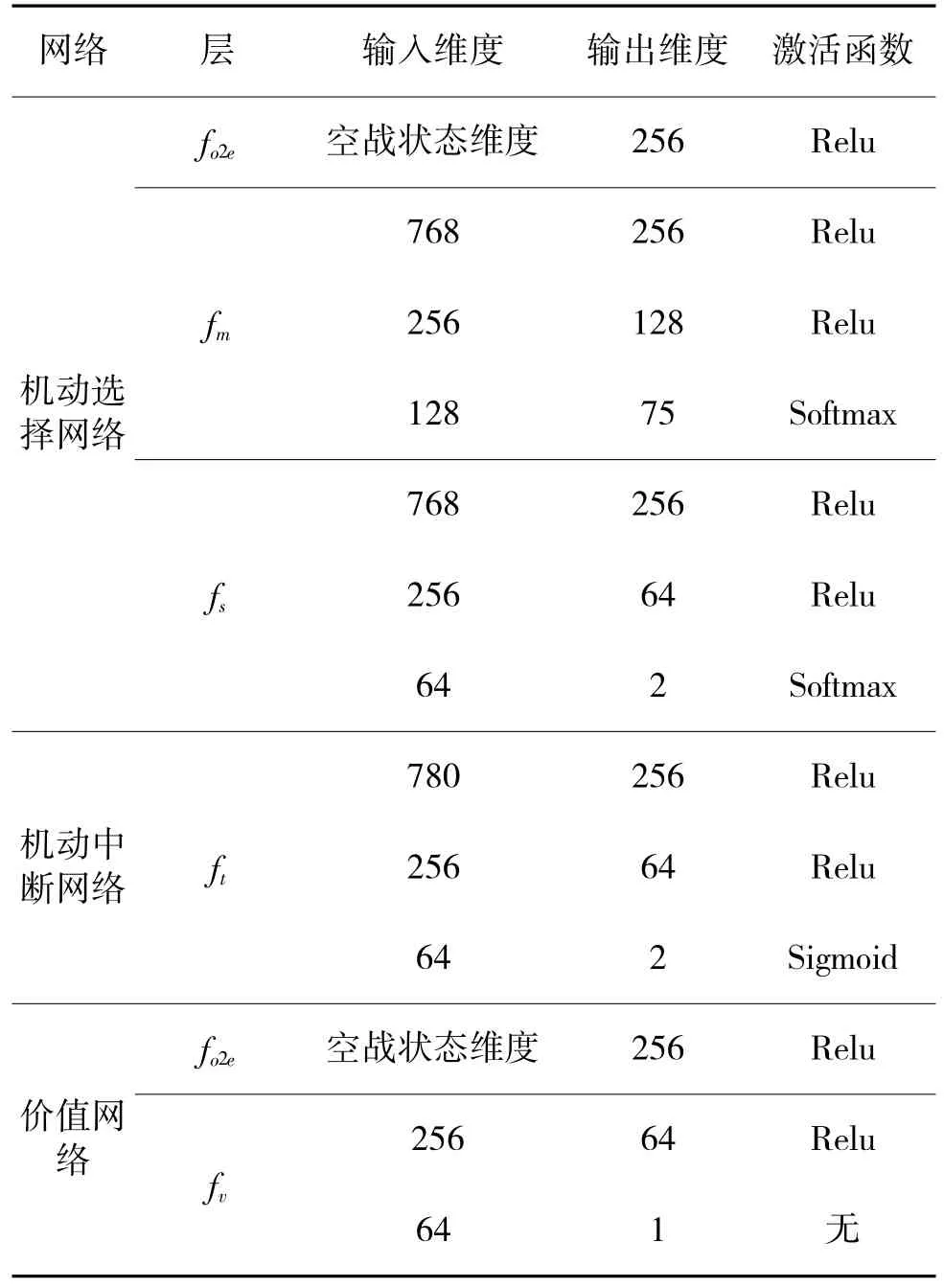
表1 分层网络结构Table 1 Hierarchical network structure

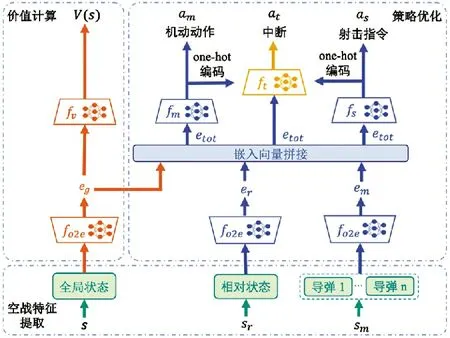
图2 分层网络框架Fig.2 Hierarchical network framework

3.3 训练过程

本文采用自博弈对抗的训练方式使其具备期望的决策能力。无人机通过与环境互动获得奖励或惩罚。表2 展示了无人机获得奖励或惩罚的典型事件。

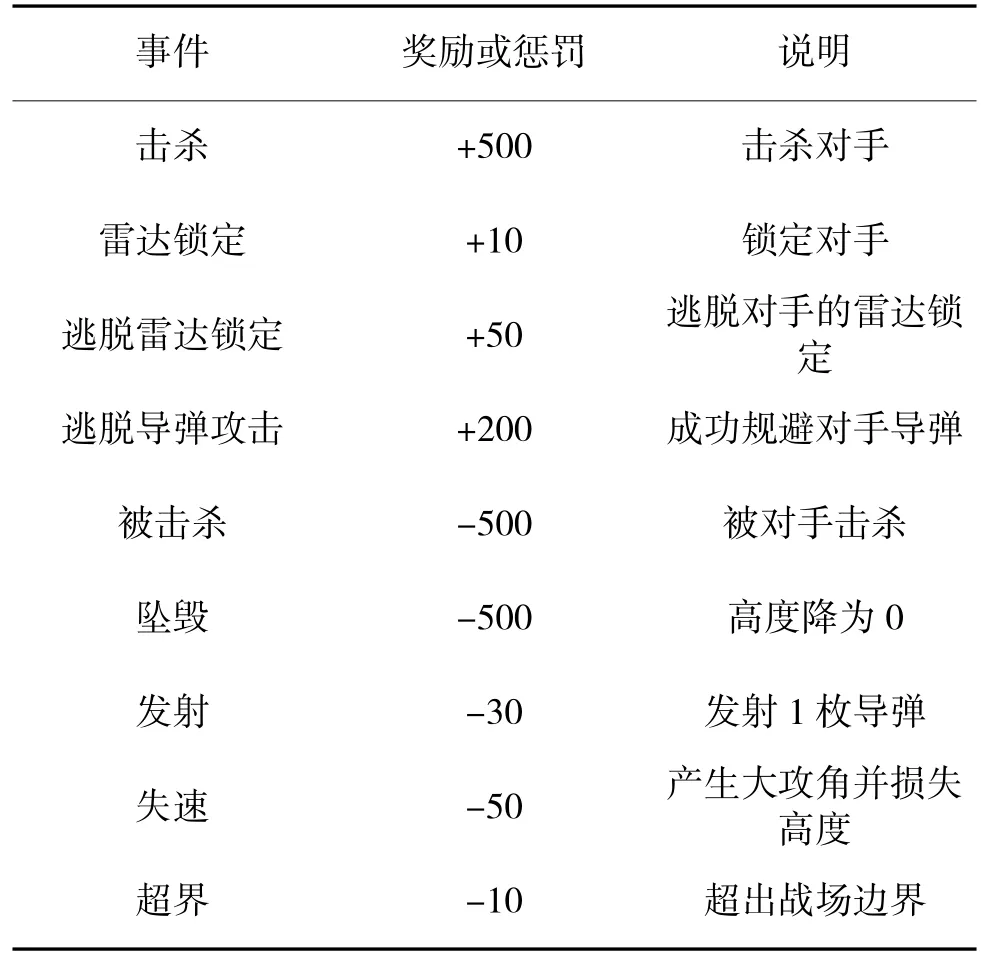
表2 奖励设置Table 2 Reward setting

基于上述分层网络，将训练过程分为采样和训练两部分。首先，初始化两架由上述分层网络参数控制的无人机。通过两架飞机与仿真环境的对抗互动，采集每个仿真步下的数据作为训练样本，共采集10 000 条样本。网络参数采用式（1）～式（3）进行更新，学习率设置为1×10-5。更新结束后，将旧样本丢弃并采集新样本。采样和训练交替进行，直到最大训练轮数。整个训练过程的具体实施步骤如下：

Step 1：初始化机动选择策略网络、机动中断策略网络和价值网络，设置动作最大保持间隔tmax，动作保持步长为0；

Step 2：将空战状态输入机动中断策略网络，输出无人机中断动作的概率p，通过参数为p 的伯努利分布进行采样，如果采样结果为1，则无人机中断当前动作；否则，维持动作不变；

Step 3：当无人机中断当前动作或动作保持步长等于最大保持间隔时，将动作保持步长重制为0，执行Step4，否则执行Step5；

Step 4：将空战状态输入机动选择策略网络，输出机动动作和相应的动作概率πα，获取即时奖励rt和下一状态st+1，将当前状态和下一状态输入价值网络，输出当前价值vt和下一状态价值vt+1。根据式（1）和式（3）更新机动选择策略网络和价值网络的参数，跳转到Step6；

Step 5：动作保持步长加1，无人机维持机动动作不变；

Step 6：根据式（2）更新机动中断策略网络的参数，循环执行Step2～Step6 直到最大训练轮数。

4 仿真验证

4.1 算法整体表现

为了验证本文提出的方法能够有效学习无人机的机动决策，将其与DQN 和DDPG 算法进行对比［8］，所有算法均选取3 个随机数种子，共训练2 000 轮。图3 展示了3 种算法的学习曲线，其中，横轴表示训练轮数，纵轴表示算法对应的无人机在训练过程中获得的平均奖励，阴影部分体现了3 个随机数种子下奖励的方差，而实线为对应的均值。从图中可以看出，本文提出的方法获得了高于-100 的平均奖励，显著优于对照算法。根据表2 的奖励设置，更高的奖励反映了更有效的进攻行为和防御性为，从而证明了本文算法能够使无人机在空战中作出更为有效的机动动作以高效击杀目标和规避威胁。

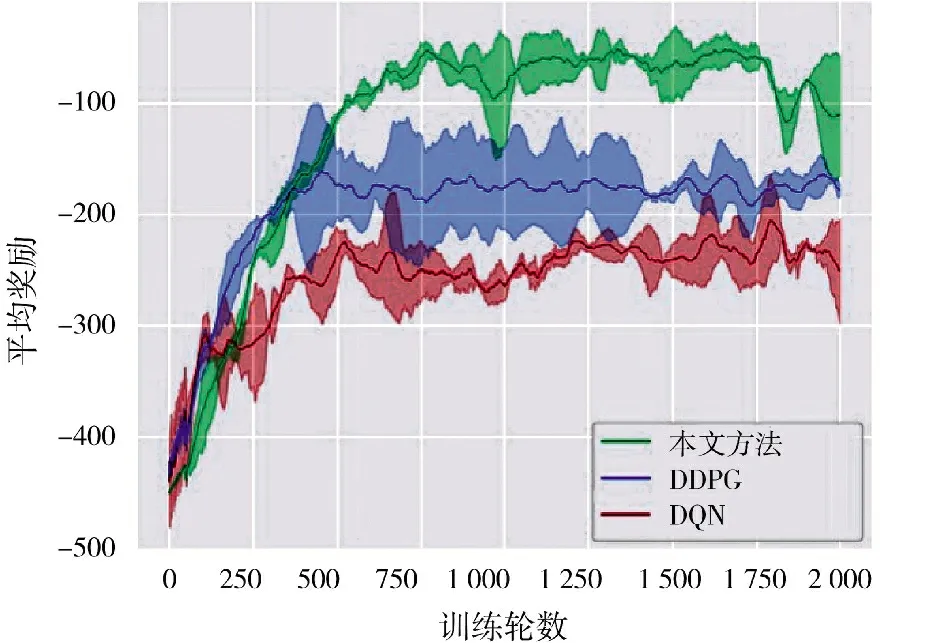
图3 学习曲线Fig.3 Learning curve

4.2 模拟空战对抗测试

将本文算法和DDPG，DQN 和基于规则的专家系统进行100 场模拟的对抗测试。无人机的初始化高度为5 km～10 km，初始化速度为250m/s～300 m/s，采用均匀分布进行初始化。每架无人机携带4 枚空空导弹。战场为200 km×200 km 的矩形区域，获胜条件为通过导弹击落对手或将对手驱赶至战场区域以外。空战的最大持续时间为600 s，若达到最大时间仍未分出胜负，则为平局。胜/平/负比例的统计结果如图4 所示。结果表明本文算法在对抗DDPG，DQN 和基于规则的专家系统时，分别获得了69%，74%和79%的胜率，证明了本文算法能够使无人机在空战中通过有效的机动完成高效击杀和规避，从而获胜。

图4 模拟空战对抗胜率Fig.4 Confrontation winning rate of simulation air combat

图5 展示了两个典型的空战机动轨迹。其中，蓝方为本文决策方法控制的无人机，红方为基于规则的专家系统。从图5 中可以看出，蓝机在面对红机时，能够采取更为灵活的机动策略，如：回转降高，偏置攻击等，证明了本文提出的方法使无人机学习到了更为灵活有效的机动战术。

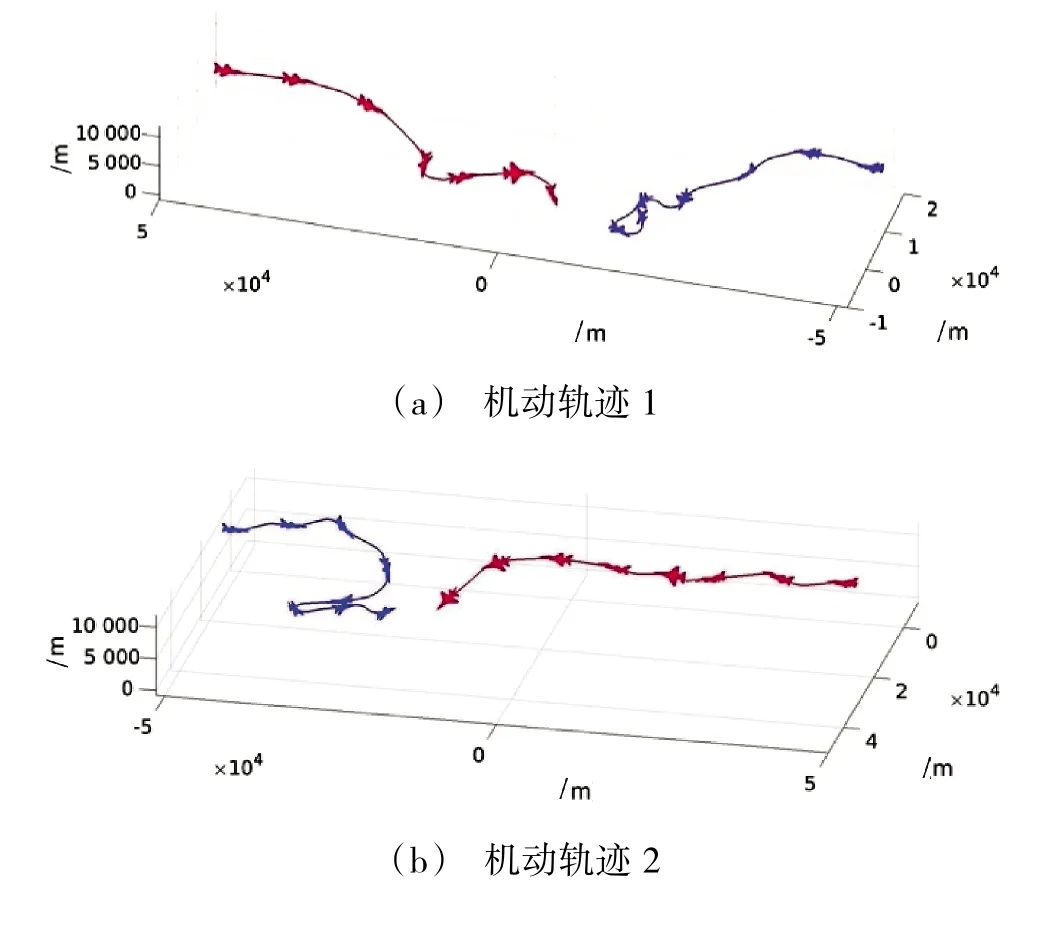
图5 基于分层强化学习的无人机机动轨迹Fig.5 Maneuver trajectory of uav based on hierarchical reinforcement learning

4.3 算法收敛性与实时性

本文算法在训练过程中如果在连续100 轮内奖励的变化不超过10%，则认为算法的训练已收敛。通过调整表1 中神经网络除输出层以外的神经元数量，观察算法的收敛轮数和平均单步决策的时间消耗，如表3 所示。实验数据表明，神经网络中神经元的数量会显著影响收敛轮数，随着神经元数量增长，收敛速度下降；而网络容量对平均单步决策用时影响不明显。

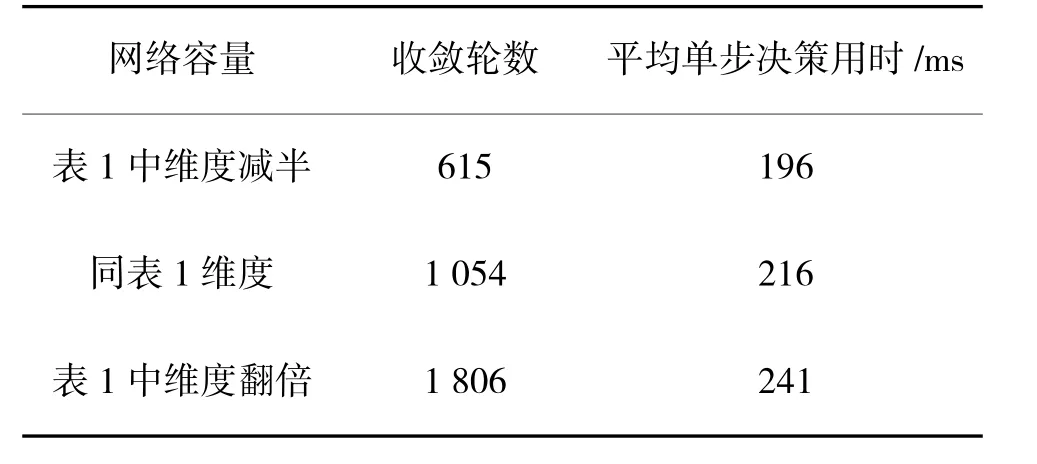
表3 算法收敛性和实时性Table 3 Convergence and real-time of algorithm

5 结论

本文提出了一种基于分层强化学习的无人机机动决策方法，设计了分层的机动选择策略网络和机动中断策略网络，推导出两种网络基于策略梯度的参数更新方式，使无人机的决策间隔能够自适应地变化，以满足高动态、强实时环境下的决策需求。