永磁同步电动机绕组匝间短路时电磁力特性的研究

成豪杰,唐 旭,李永枭

(青岛理工大学 信息与控制工程学院,青岛 266525)

永磁同步电机具有控制性能好、运行效率高以及结构简单等优势,广泛应用在交通、工业等各个领域中。由于电机的运行环境复杂,电机绕组长期发热、绝缘老化等容易导致电机绕组出现匝间短路故障。如果故障不能及早处理,将会引起更严重的相间短路等故障[1-2]。当电机发生匝间短路故障时,电机的三相电流、电磁转矩和反电势等参数也发生改变,为研究电机匝间短路故障所带来的影响,有学者建立电机匝间短路故障分析模型,对匝间短路下的转矩、相电流和短路线圈电流特性进行了分析,为诊断电机此类故障提供了依据[3-9]。当电机出现匝间短路时,电机气隙磁场发生变化,短路线圈会产生与旋转磁动势相反的磁动势,容易增强电磁振动,加重电机噪声从而影响正常使用。永磁电机的噪声一般有机械噪声、电磁噪声和空气动力噪声三种类型,电磁噪声是产生电机噪声主要原因[10],其主要是由作用于电机定子铁心内表面的径向电磁力激发的。永磁同步电机在实际使用中往往采取变频供电,这样会引入不同频率的电流谐波,这些电流谐波感生的谐波磁场作用于定子铁心上产生不同频率的径向电磁力。对于径向电磁力的分析有解析法和有限元法[11-16],于莫岩等[17]、李晓华等[18]通过解析法和有限元法分析了变频供电下径向电磁力与谐波电流频率的关系,得出了电机产生高频噪声的主要原因,但是这些分析只是在电机无故障情况下进行的,而电机故障情况下的振动噪声更加严重。

目前对于永磁同步电动机匝间短路下的电磁振动分析较少,为了分析变频供电下电机发生匝间短路时的电磁振动,本文通过解析分析电机匝间短路下的磁动势分布,建立了电机匝间短路故障下径向电磁力的解析分析模型,得到了电机径向电磁力的阶次和频率成分,然后搭建了变频供电下绕组匝间短路故障的有限元联合仿真模型,通过有限元分析验证了电机匝间短路故障时径向电磁力的解析分析模型及其阶次和频率成分分析的正确性。

1 永磁同步电动机径向电磁力的分析

依据麦克斯韦应力法,电机的径向电磁力密度为

(1)

式中:μ0为空气磁导率;θ为气隙圆周角;Br(θ,t)为径向气隙磁密分布;Bt(θ,t)为切向气隙磁密分布,与径向气隙磁密相比,电机的切向气隙磁密可以忽略不计。

当电机发生匝间短路故障时,电机的径向气隙磁密分布可以表示为

Br(θ,t)=F(θ,t)Λ(θ,t)=[Fs(θ,t)+FPM(θ,t)+Fgξ(θ,t)+FD(θ,t)]Λ(θ,t)

(2)

式中:Fs(θ,t)为定子绕组基波电流产生的磁动势;FPM(θ,t)为转子永磁体磁动势;Fgξ(θ,t)为绕组谐波电流产生的磁动势;FD(θ,t)为短路线圈产生的脉振磁动势;Λ(θ,t)为气隙磁导函数。

将式(2)代入式(1)可得:

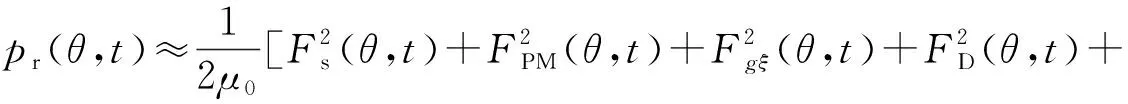
(3)

对转子永磁体磁动势、定子基波电流磁动势、谐波电流磁动势、脉振磁动势和气隙磁导函数分别进行傅里叶展开,代入式(3)即可得到径向电磁力密度的解析分析模型。

1) 永磁体磁动势FPM(θ,t)的傅里叶展开式为

FPM(θ,t)=∑Fμ1cos(μ1ωt-μ1pθ)

(4)

式中:μ1=1,3,5,…;ω为电机转子旋转的电角速度;p为电机的极对数。

(5)

式中:μ2=1,2,3,…。

2) 三相对称定子绕组基波电流磁动势Fs(θ,t)的傅里叶展开式为

(6)

所以该空间磁动势为

Fs(θ,t)=∑Fvcos(ωt-vpθ+φ)

(7)

式中:φ为A相绕组轴线与永磁磁极中心线的夹角;v=±6n+1(n=0,1,2,3,…)。

3) 三相对称定子绕组电流谐波磁动势的傅里叶展开式为

(8)

式中:g为谐波电流的次数;ξ= ±6n+1(n=0,1,2,3,…)为谐波电流产生的磁动势谐波阶数。

该谐波电流主要有两种:低频电流谐波频率fg= (±6k+1)f1,其中,k=0,1,2,3,…,f1为电流的额定频率;开关频率附近的高频电流谐波频率fg=afc±bf1,其中,fc为控制电路的开关频率,当a=1,3,5,…时,b=3(2m-1)±1, (m=0,1,2,…);当a=2,4,6,…时,b=6m±1, (m=0,1,2,…)。开关频率附近的主要谐波电流的频率为afc±2f1,afc±4f1,afc±8f1(a为奇数)和afc±f1,afc±5f1,afc±7f1(a为偶数)等。

4) 定子绕组发生匝间短路时,如图1所示。图1中,A相绕组一个定子槽内的部分线圈发生了匝间短路。

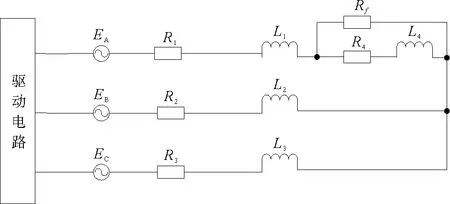
图1 匝间短路故障

在图1中,A相绕组未短路线圈的电流为ia1=iA1+iA2。其中,iA2是与B相、C相电流对称的分量,即iA2=-iB-iC,而iA1是由于A相短路导致的A相电流大于B相、C相电流的分量。同时,A相绕组短路线圈中只存在转子永磁体旋转产生的感应电流ia2=iAD,为了方便分析,将短路线圈的电流写为ia2=ia1-ia1+iAD= (iA1+iA2)-ia1+iAD。

此时,B相、C相电流与A相绕组(包含未短路线圈、短路线圈)电流分量iA2构成三相对称电流,所产生的空间磁动势如上述第2)、3)项所示。另外,A相绕组其余电流分量在空间产生的是脉振磁动势,现分析如下:

①A相绕组未短路线圈、短路线圈的电流分量iA1产生的脉振磁动势为F1coshpθcosgωt,h=1,3,5,…。

②A相绕组短路线圈的电流分量-ia1,iAD产生的脉振磁动势为F2coslθcosgωt,l为正整数,且不等于Q1/y的整数倍,其中Q1为定子槽数;y为短路线圈的节距。

则总的脉振磁动势为

FD(θ,t)=(F1coshpθ+F2coslθ)cosgωt

(9)

5) 气隙磁导函数的傅里叶展开式为

Λ2(θ,t)=G01+∑Gk1cosk1Q1θ

(10)

式中:G01为气隙磁导的恒定分量;Gk1为气隙磁导k1次谐波的幅值,k1=1,2,3,…;Q1为定子槽数。

将式(4)—(10)代入式(3),可以得到永磁同步电动机故障时的径向电磁力密度解析分析模型。经分析,电磁力的阶次和频率成分见表1。

与电机正常状态下相比,电机发生匝间短路故障时,电磁力的阶数和频率发生变化,会产生低阶的电磁力,例如阶数为l1±l2,hp±l,μ1p±l和νp±l等的低阶电磁力。

在SVPWM调制策略下,主要的高频谐波电流频率为fc±2f1,fc±4f1和2fc±f1,产生的径向电磁力的阶次和频率成分见表2。

表2 高频谐波磁场作用产生的电磁力的阶数、频率成分

2 内置式永磁同步电动机的有限元分析

2.1 电机联合仿真模型的建立

本文研究的是一台11 kW、6极36槽内置式永磁同步电动机,其出现匝间短路故障时的模型如图2所示,红色线圈为匝间短路线圈。电机主要参数见表3。

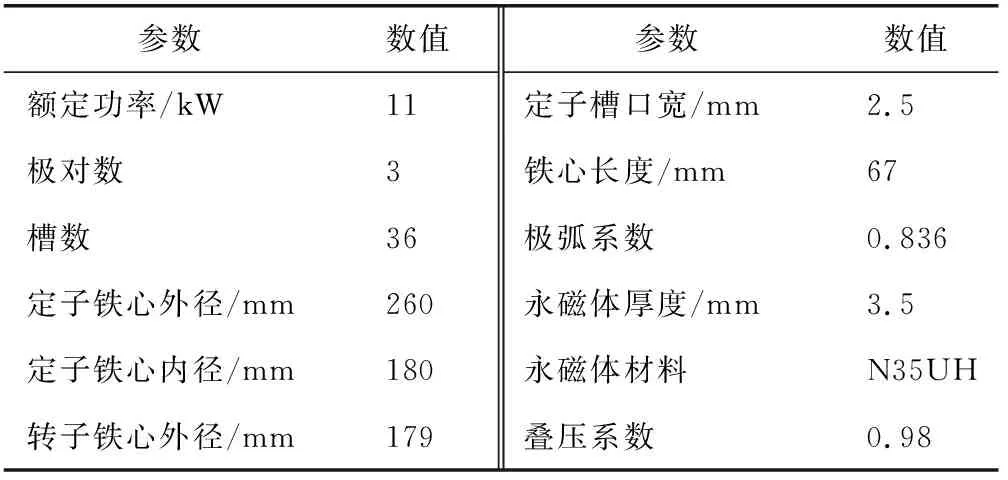
表3 样机的主要参数

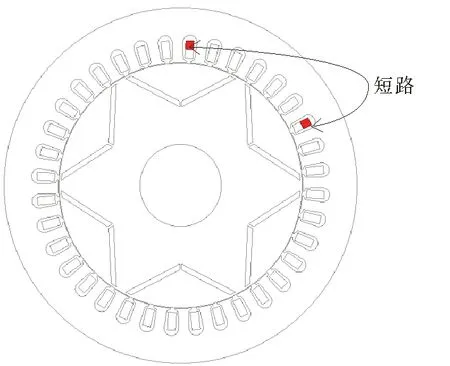
图2 样机匝间短路故障

变频供电下,为分析匝间短路故障对永磁同步电动机径向电磁力的影响,搭建基于矢量控制的联合仿真模型,图3为联合仿真模型的控制电路,图4为联合仿真模型的逆变驱动电路。电机每个定子槽内的绕组匝数为17匝,设置A相匝间短路匝数为8匝,R1为匝间短路线圈的电阻,L1为匝间短路线圈的端部电感。将电机有限元模型、矢量控制电路与逆变驱动电路连接,在控制模型中设置SVPWM载波频率为4 kHz,驱动电路中6个功率器件IGBT的通断由SVPWM输出状态信号进行控制。

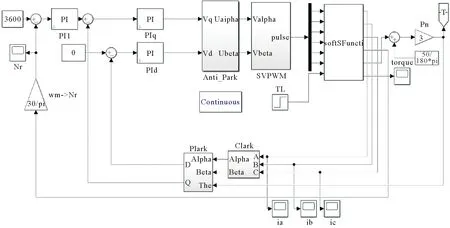
图3 联合仿真模型的控制电路

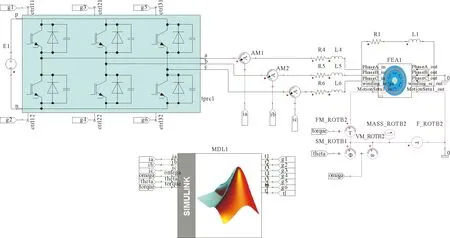
图4 联合仿真模型的逆变驱动电路

2.2 谐波电流的有限元仿真分析

利用所建立的联合仿真模型对电机的负载运行情况进行有限元仿真,并进行电流谐波分析,其中控制电路的开关频率为4 kHz,电源的额定频率为180 Hz。图5、图6分别为电机无故障、匝间短路故障下稳定运行后的三相电流波形。对A相电流分别进行傅里叶分解得到的频谱图如图7、图8所示,右上角为局部放大图。图9、图10为短路线圈电流波形和频谱图。

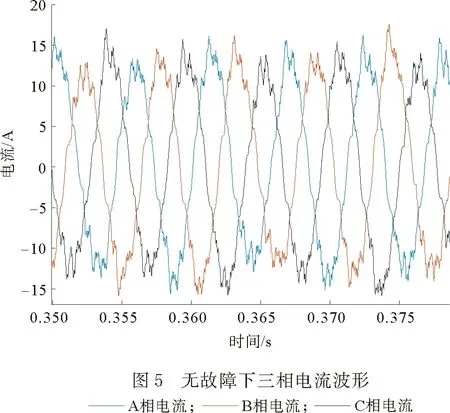
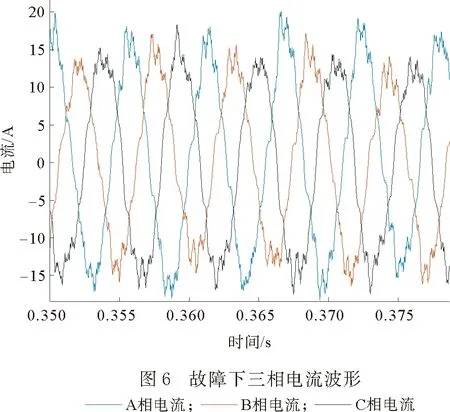
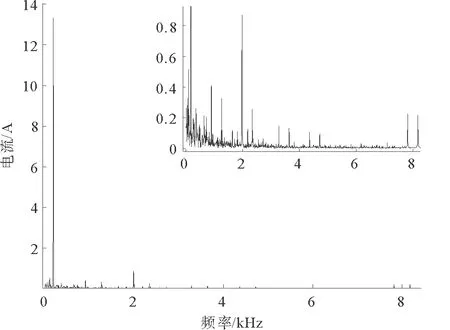
图7 无故障下A相电流频谱

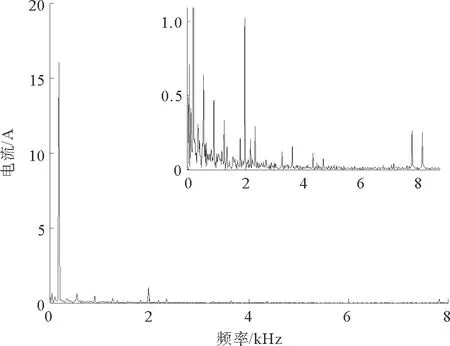
图8 故障下A相电流频谱

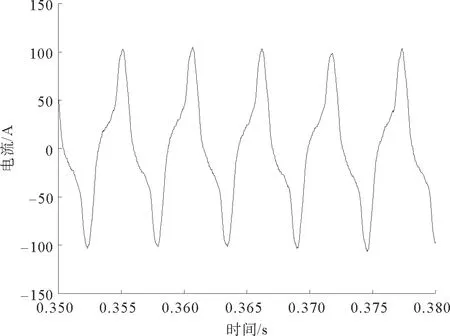
图9 短路线圈电流波形

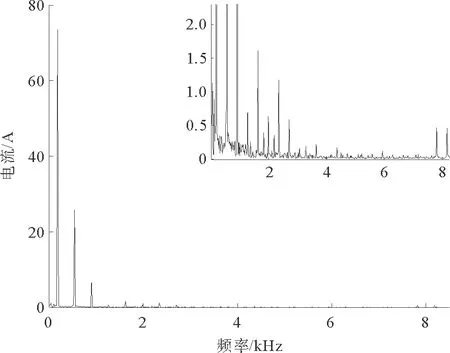
图10 短路线圈电流频谱

当电机匝间短路故障时,三相电流不对称,故障相电流比其他相电流幅值大,A相电流幅值为16.05 A,相比正常状态下增大了20.4%;频率为180,1260,1980,2340 Hz的A相电流幅值比正常状态下幅值高,短路线圈电流幅值远远大于正常电流,可能会进一步烧坏匝间绝缘,造成更多线圈短路。从图5和图6中可以看出,电流波形接近正弦波,但是里面含有大量的谐波导致电流波形发生畸变,在变频供电下,绕组电流的低频频率主要有180,900,1260,1980和2340 Hz等,与理论分析fg=(±6k+1)f1相符;开关频率附近的高频频率成分主要有3280,3640,4360,4720,7820和8180 Hz等,已知fc=4 kHz,f1=180 Hz,有限元仿真结果也与理论分析fg=afc±bf1相符。

2.3 径向电磁力的有限元仿真分析

图11、图12分别为电机无故障、匝间短路故障下某一瞬间作用于定子铁心内表面的径向电磁力密度分布图,分别对其进行傅里叶分解可以得到径向电磁力密度的主要空间阶次成分,如图13、图14所示。由图11、图12可以看出,匝间短路故障下电磁力分布不均匀,故障下径向电磁力幅值比正常状态下大。由图13、图14可以看出,电机正常情况下径向电磁力的空间阶次主要为6,12,18,24,30阶。由表1得电磁力主要阶次为2p的整数倍,解析分析与有限元分析的结果相符;匝间短路故障下附加产生了1,2,4,5,7阶等一些低阶的径向电磁力,由表1得脉振磁动势作用下的低阶电磁力阶次为l1±l2,hp±l,μ1p±l

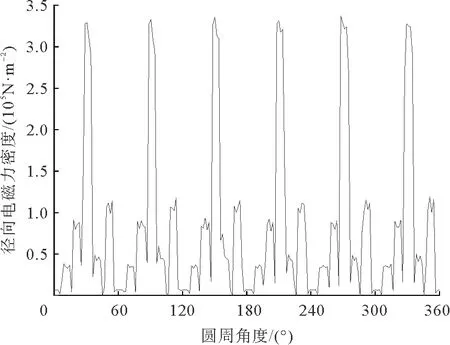
图11 无故障下径向电磁力密度波形

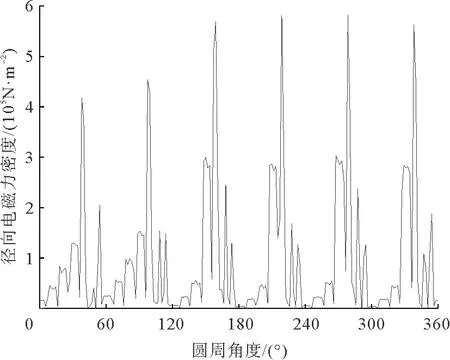
图12 故障下径向电磁力密度波形

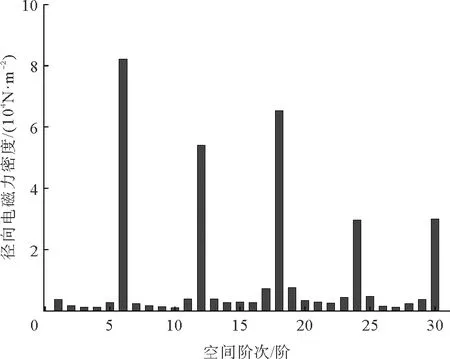
图13 无故障下径向电磁力密度空间阶次

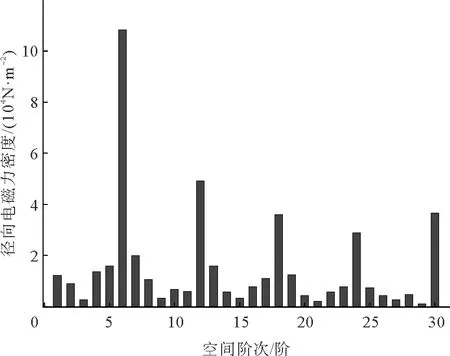
图14 故障下径向电磁力密度空间阶次

和vp±l等,解析分析与有限元分析的结果相符。

电机稳定运行之后,对电磁振动产生主要影响的是6阶径向电磁力。因此,本文计算了电机无故障、匝间短路故障下,转子旋转一周的时间内(0.0167 s),电机定子齿顶处6阶径向电磁力随时间变化曲线,分别如图15、图16所示。对其进行傅里叶分解得到相对应的频谱图,如图17、图18所示,右上角为局部放大图。由图17、图18可以看出,电机正常状态和发生匝间短路故障时6阶径向电磁力密度的主要频率成分为360,720,1440,1800,2520,3100,3820,4180,4900,7640和8360 Hz等。其中在频率360,1080,1800,2160,2520 Hz下,故障状态的径向电磁力密度比正常状态下大,所以匝间短路故障增强了电磁振动。由表1和表2可知,对于该样机,正常状态下和匝间短路故障下产生的6阶径向电磁力低频频率均为2f1,(g1±g2)f1,(g±1)f1;开关频率附近的电流谐波产生的6阶径向电磁力频率均为fc±f1,fc±5f1,2fc±2f1,这与有限元仿真结果相同。

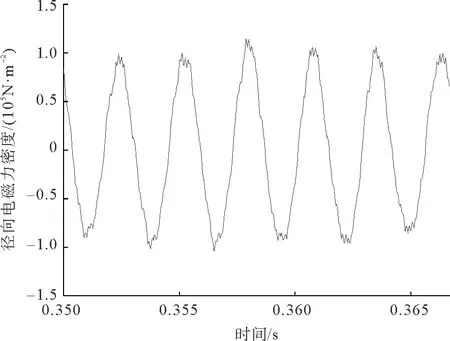
图15 无故障下定子齿顶处6阶径向电磁力密度

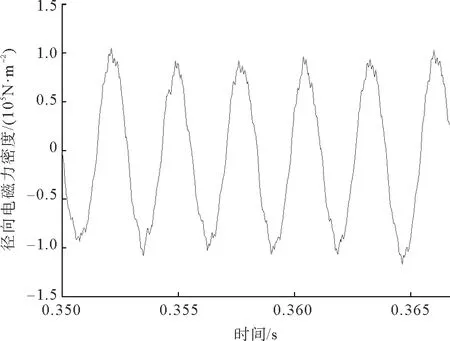
图16 故障下定子齿顶处6阶径向电磁力密度

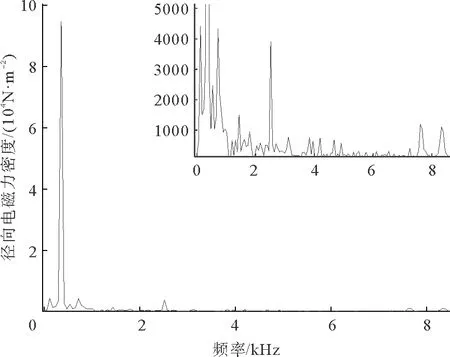
图17 无故障下6阶径向电磁力密度频谱

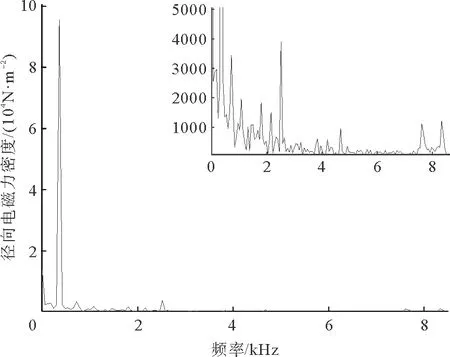
图18 故障下6阶径向电磁力密度频谱

由前述分析可知,电机发生匝间短路故障时,会出现低阶电磁力,因此进一步分析了新出现的低阶电磁力的频率成分。同分析6阶径向电磁力一样,利用有限元计算和傅里叶变换可以得到1,2,4,5,7阶径向电磁力的主要频率成分及对应的幅值,见表4。电机定子齿顶处5阶径向电磁力密度频谱图如图19所示。由表4可以看出,1,2,4,5,7阶径向电磁力的主要频率为360,720,1080,1440,1800,和2160 Hz等低频部分,开关频率附件的高频部分幅值较小;由表1可知,新产生的低阶电磁力的主要频率成分相同,且为(g±μ1)f1,(g±1)f1和(g1±g2)f1,该结果与有限元分析结果相符。同时,由表4可以看出,随着频率变大,电磁力幅值趋于减小,其中对低阶电磁力产生主要影响的频率是360和720 Hz。

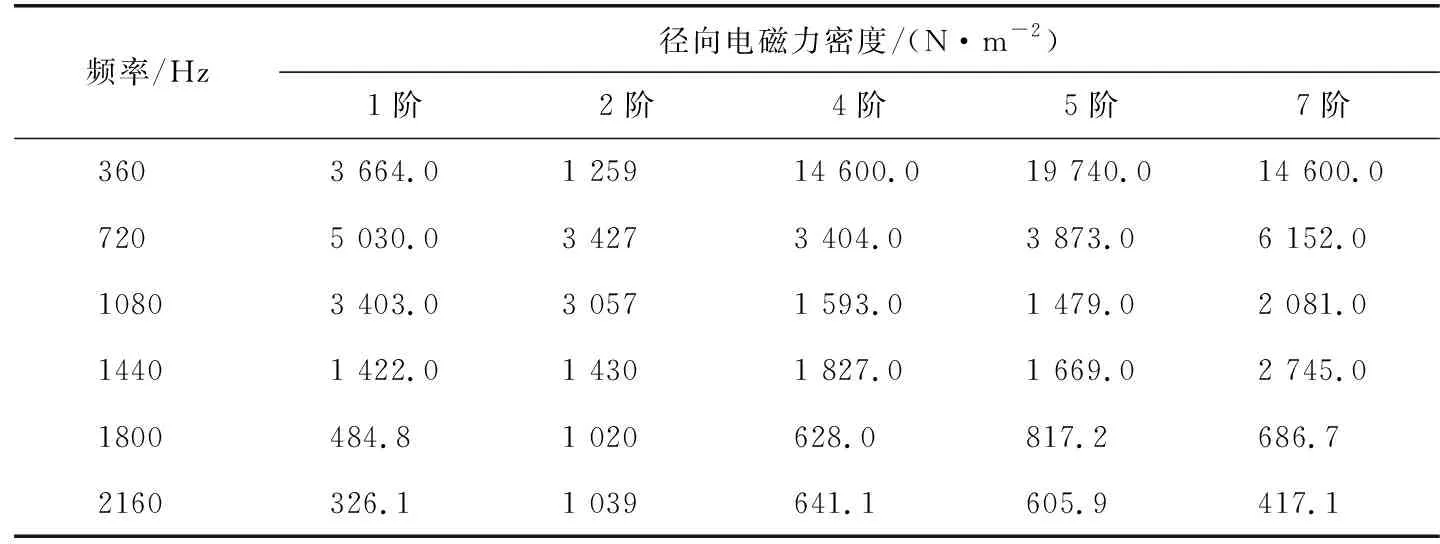
表4 匝间短路故障产生的低阶电磁力的幅值

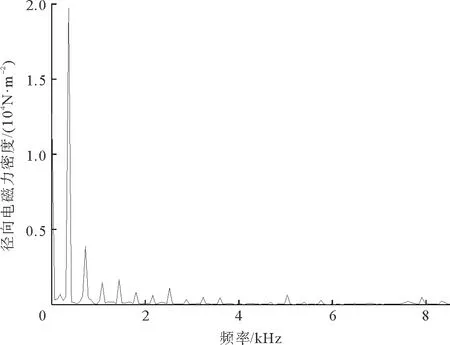
图19 故障下5阶径向电磁力密度频谱

3 结论

本文建立了永磁同步电动机发生匝间短路故障时径向电磁力的解析分析模型,分析了无故障和故障下径向电磁力的阶数和频率成分特征;另外,建立了电机本体和控制电路结合的联合仿真模型,分别在无故障和故障情况下对电机径向电磁力的阶数和频率成分特征进行了有限元仿真验证。得到以下结论:当电机发生匝间短路故障,三相电流不平衡,故障相电流的幅值比其他相的大,电机故障时的谐波电流频率成分与无故障时相同;无故障时电机的径向电磁力阶次主要为2p的整数倍,故障下电机中会产生低阶的径向电磁力;电机无故障、故障下相同阶次电磁力的频率成分相同,且均包含低频成分和高频成分;电机故障下新出现的低阶电磁力的主要频率成分相同。