融合公交GPS与IC卡数据的乘客下车点推算模型研究及应用
2023-10-24周晨阳张国栋文舜智欧阳锦灿
周晨阳 张国栋 文舜智 刘 川 欧阳锦灿
(浙江数智交院科技股份有限公司,浙江 杭州 310030)
公共汽车作为县城公交系统的重要组成部分,对公交GPS和IC卡数据进行研究得到乘客出行的需求与规律,为公交线路规划调整、运营管理提供数据支撑[1-3]。推测公交下车点可以了解公共交通需求变化特征。针对公交下车点推算的研究较多。Farzin[4]通过整合公交GPS数据估算乘客出行的上下车位置,构建区域公交OD矩阵。Vu等[5]构建了一个用于用户聚类和目的地预测的朴素贝叶斯分类器。Chen等[6]利用智能卡数据比较了伦敦、北京和新加坡的异质性和多样性,讨论不同时空尺度的变化。Eh等[7]从城市、分析方法、输出结果等方面对使用IC卡数据估计公共交通OD进行了综述。Yan等[8]通过制定往返、换乘原则识别出行的用户,利用朴素贝叶斯分类器完成下车点识别。综上所述,公交下车点推断主要有两种识别方法:一是基于出行链,该方法逻辑简单,适用于小样本且具有明确应用场景的数据;二是基于机器学习,需要有大量数据支撑,适用于出行链规则不明确的应用场景。文章以浙江省某县为例展开研究,该县公交线网结构清晰,居民公交出行行为、出行链及活动模式异质性较低,可采用基于规则的识别方法推算公交下车点,对推算结果进行客流特征分析。
1 公交数据概述
基于2020年9月1日—11月30日浙江省某县的公交GPS数据和IC卡数据展开。区域总面积2 539 km2,2020年常住人口19.4万人,有19条公交线路,209个公交站点。本文使用的公交GPS数据约2 000万条,IC卡数据约37.3万条。根据该县2020年公交乘车类型分布调查,9—11月乘车人次共计约41.8万人,IC卡(含客票、月票、公交云)占比为89.5%,该县公交IC卡普及率较高,因此使用IC卡数据进行下车点推断及客流出行特征挖掘具有一定代表性。
各乘车类型数量分布如表1所示。
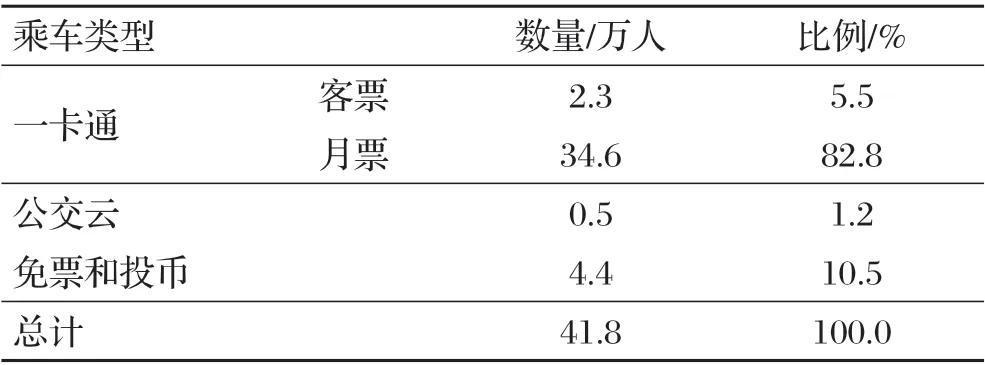
表1 各乘车类型数量分布
2 基于时空约束与概率的两阶段下车点推算模型
将公交GPS数据和IC卡数据匹配,通过将IC卡数据匹配对应车辆指定时间段内的GPS数据,得到站点上客记录表,通过融合时空信息和概率方式的两阶段模型推算下车点。基于出行链时空约束的推算模型:先基于时间和位置推算,对每个上客站点,找到下个刷卡时间站点,当前线路中与其最近的站点即为下客站点;基于概率的推算模型:面向非通勤出行的公交记录,且时空约束推算模型失效情况下,选择用户在当前线路上客频率最高的站点作为下客站点。
2.1 基于出行链时空约束的推算模型
经典出行链包含两点基本假设。同一出行者行程连续,即前一段行程下车点和接续行程上车点在时空上相近;同一出行者单日出行链闭环,单日行程结束时返回当日出发站点。文章构建了基于时空约束的出行链假设以保证推断过程的准确性。根据同一用户出行记录判断用户“往返”“同站换乘”“异站换乘”3种类型出行记录并打上标签。针对同站换乘类型,检查前后两程是否满足同站换乘时间上限来判别其有效性;针对异站换乘类型,只有同时满足时间约束和空间约束时,记录才有效。同站换乘和异站换乘的时空约束应该有所差异。
基于时空约束的出行链假设下车点推算模型如图1所示。

图1 基于时空约束的出行链假设下车点推算模型
2.2 基于概率面向弹性出行的下车点推算模型
上客记录总数为n,对于第i条上客记录ri(1 ≤i≤n),卡号为ci,刷卡时间为ti,所属公交线路为l(共m个站点,站点集合Lm={l1,l2,…,lm}),点为SUi,要推算的下客站点为SDi,推算步骤为:筛选出卡号为ci,且与ri同日期,刷卡时间大于ti的上客记录集,记为R;若R非空,则找到离推算上客记录最近的一次上客记录rj(j≠i,1 ≤j≤n),将rj的上客站点记为SUj,线路l中离站点SUj最近的站点作为推算的下客站点,时,满足Distance(Sp,SUj)最小,则SDi=Sp。其中Distance(S1,S2)表两个站点的距离;若R为空,则筛选出卡号为c且线路为l的所有上客记录集,统计上客站点频率,排除上客站点SUi后,由高到低排列为{S1,S2,…,Sm},则上客频率最高的站点S1作为推算的下客站点,即SDi=Sp。每条上客记录ri采用以上步骤推算下客站点,可得到站点上下客记录表。面向弹性出行的第二阶段推算模型较好地弥补了第一阶段推测效率较低的缺陷。
两阶段下车点推算模型整体框架如图2所示。

图2 两阶段下车点推算模型整体算法框架
3 下车点推算结果及县城公交客流特征分析
3.1 上下车点推算模型结果分析
两阶段模型在整体下车点推算比例为96.6%,共计约25.5万条。其中第一阶段基于出行链时空约束的推算比例为41.7%,第二阶段基于概率面向弹性出行的下车点推算比例为54.9%。
下车点推测各阶段数量占比如表2所示。
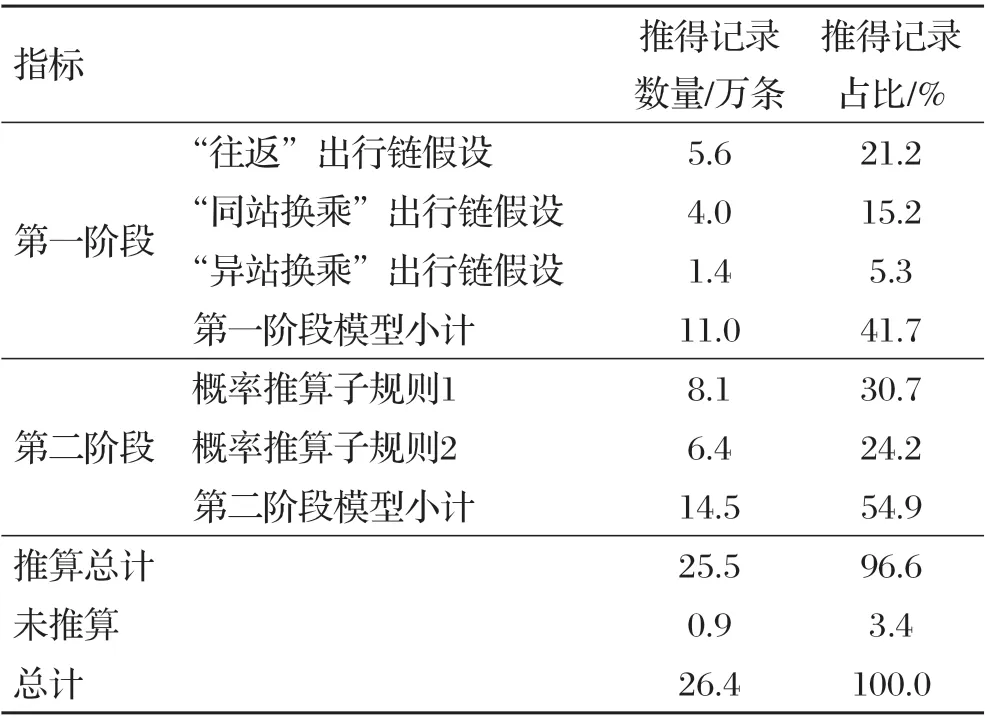
表2 下车点推测各阶段数量占比
在推得上下车站点记录的基础上,以4路为例,从站点上下客日人次、站点OD日人次、运距、客流等维度进行分析。4路各站点上下客量较大的人民医院、官碧路口、平昌广场西站点均为建设强度或居住密度较高区域。
4路站点上下客日人次如图3所示。
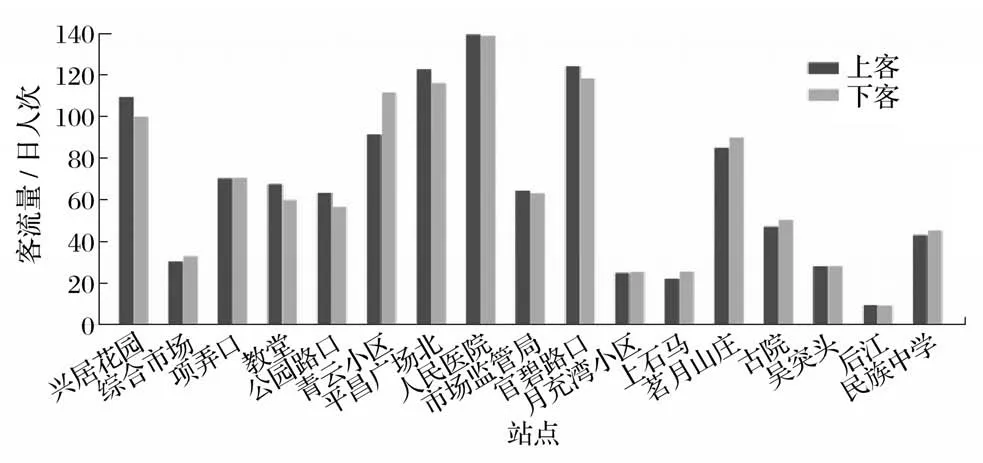
图3 4路站点上下客日人次
4路OD量的分布不太均衡,少数主要场所承担了很大的OD量,如广场、医院、公园等,这些场所都有客流聚集的风险,原因可能是县城用地规划各功能分区的不协同性,在无形中增加了该县公交的客流负担。4路站点日均OD矩阵如图4所示。
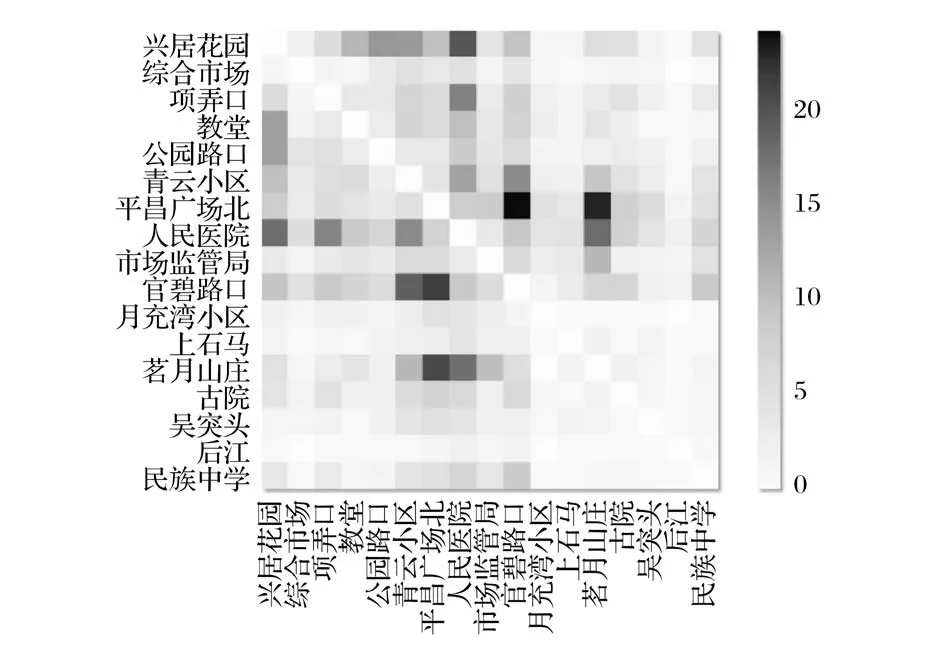
图4 4路站点日均OD矩阵
1路、6路总运距最高,5路、6路平均运距最高,与1路、5路、6路途径工业园区、公司、学校等有关,会产生大量通勤出行。各人次运距变化总体平滑,但前20%人次运距变化幅度较大,说明公交出行倾向于短途。各线路平均运距对比如表3所示。
3.2 基于下车点推断的县城公交客流分析
3.2.1 高低频客流分析
将月出行次数大于15次的乘客定义为高频客流,反之为低频客流。低频客流的平均出行距离大于高频客流,高频乘客倾向于更短距离的出行。另外该县20.9%的高频用户数贡献了67%的客流量,表明少量高频用户承担了大部分县城公交出行,应当作为公交运营管理的重点关注对象。
高低频客流特征对比如表4所示。
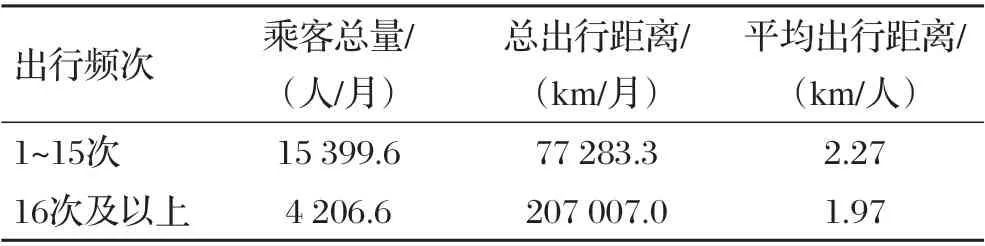
表4 高低频客流特征对比
3.2.2 分时段客流分析
以10 min为间隔,分别统计工作日和休息日在各时间段的客流,如图5、图6所示。

图5 工作日分时段客流变化趋势
从总体客流量分布可知,3个月的客流时变趋势基本一致,10月份因为国庆假期导致工作日客流少而节假日客流多;从各时段的分布上看,工作日和节假日均呈现出早高峰和晚高峰的特征,工作日更明显且早晚高峰时间集中,说明工作日承担了大量的通勤客流,休息日相对特征不明显且时间比较分散,说明休息日承担了大量的非通勤客流。
4 公交特征规律对于其他县城的适用性
为了验证规律对一般县城的适用性,对浙江省其他2个县(SY县、LG县)同样使用二阶段下车点推算模型及公交客流特征分析,以SC县表示本研究案例县城。
各县基本情况如表5所示。
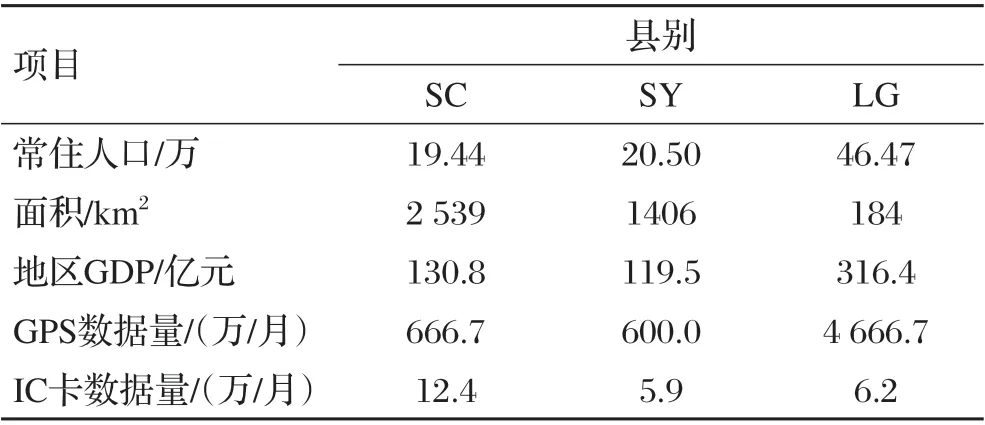
表5 浙江省各县基本情况
由表5可知,人口、地区GDP和数据量上SC、SY两县接近,LG县大于SC、SY两县,但LG县区域面积较小,人口密度远大于SC县、SY县,总体各县人口规模处于同一数量级,具有可比性。
模型推算各县部分客流结果数据如表6所示。

表6 各县部分客流结果数据
两县的各项结果相近,SY县高频用户和高频流量比例都更高,共同规律是少量高频用户占了大部分客流量,低频用户的平均出行距离大于高频用户,工作日相比休息日平均出行距离略大、每日客流量更多,高频用户倾向于工作日出行,低频用户倾向于休息日出行。推算SY、LG两县的上下客日人次、站点OD量、运距指标,规律也与SC县一致,说明SC县分析得到的特征规律适用于一般县城。
5 结语
文章基于浙江省某县2020年9—11月的公交GPS数据和IC卡数据,进行下车点推算及其应用,设计了融合时空信息和概率方式的两阶段下车点推算模型,得到该县公交系统OD矩阵。从站点OD量、运距、客流等维度展开分析,得到规律基本符合实际县城实际情况,采用同样模型和方法对相似的县城进行分析验证,发现结论也适用于其他县城,如各站点上下客量总体均衡,平时客流密集站点的上下客量较大;线路OD分布总体不均衡,少数场所承担较大OD量;不同线路总运距和平均运距不同,各人次运距变化总体平滑,公交出行倾向于短途;工作日相比于休息日平均出行距离略大、每日客流量更多,高频用户倾向于工作日出行,低频用户倾向于休息日出行;工作日和节假日都呈现早高峰和晚高峰的特征。文章所设计公交下车点推算方法与站点OD、运距、客流等的规律特征,对县城公交均具备一定普适性。文章也存在一些不足,主要体现在下车点推算方法上,对于刷卡频率较低的乘客,难以通过基于时空信息和概率的方法推算,后续可以完善相关方法,或采用将规则与机器学习相结合的方法,对公交下车点进行更精准推算。
