基于循环模型的盾构隧道地铁列车行车性能分析

牛 刚，张光伟，靳兆阳，张 伟

（1. 中交海峡建设投资发展有限公司，福建福州 350015；2. 中国交建轨道交通分公司，北京 101300；3. 福建理工大学土木工程学院，福建福州 350118）

1 引言

随着城市轨道交通运营网络的增密以及运营速度的持续提升，对城市轨道交通运营的安全性和稳定性的要求愈发严格[1]。盾构隧道凭借其独特的优势，逐渐成为地下空间开发的主要技术手段。地铁列车对隧道及周边环境的影响，以及列车在隧道中的振动现象，均是隧道建设的重点研究内容。一些学者已在这方面做出了贡献：王晓睿等[2]以郑州地铁1号线为背景，探讨了地铁列车在小半径曲线盾构段的隧道周边土体动力响应；夏志强等[3]针对杭州地铁3号线，建立地铁车辆-轨道耦合振动模型，分析了浮置板长度、轨道不平顺、扣件刚度等因素对钢弹簧浮置板轨道动力特性的影响；周华龙等[4]同样构建了地铁列车-轨道耦合振动模型，并以深圳地铁某线路为研究对象，讨论了不同等级减振轨道对运行性能的影响；董昊亮等[5]以上海地铁为背景，构建车轨耦合模型，讨论了地铁车轮磨耗对地铁运行平稳性的影响；魏焕卫等[6]以济南地铁为背景，对地铁运行引发的环境振动进行了监测，对响应的时频特征及传播规律进行了分析。国际学者如Zhang等[7]以成都市1条紧邻既有地铁1号线的地铁隧道为研究对象，通过现场试验和数值计算，分析了新建地铁隧道在既有线列车移动荷载作用下的车辆动力响应特性；Yang和Li[8]提出了一种基于三维动态刚度的模型（DSM），以预测地铁列车引发的建筑物振动。

在盾构隧道的设计与施工前期计算过程中，常需进行有限元计算，分析盾构管片的受力情况及变形状态。由于隧道长度较长，精细化的有限元分析需要大量的自由度，从而耗费巨大的计算内存和时间。例如，在对盾构隧道地铁列车行车性能进行数值分析时，列车需行驶一段较长的距离，导致结构部分的计算范围过大。然而，列车经过一段时间后，前一段距离的盾构结构对列车行车性能的影响变得微小。鉴于此，本研究提出了一种循环计算方法，该方法将盾构结构首尾相接，形成闭环，使得数值模拟的列车可在闭环内进行循环计算，由此减少所需的自由度，有效提升计算效率。

2 土体-盾构管片循环模型

土体和盾构管片通过有限元软件ABAQUS建模，如图 1所示，二者均为实体单元，盾构管片与土体之间采用Tie接触，即不考虑二者之间的滑移，土体外部为固定边界，将土体及盾构的前后两边进行耦合处理，实现类似“共节点”的状态。完成建模后将土体-盾构模型的刚度和质量矩阵导出。

图1 土体-盾构管片有限元模型

3 列车-轨道-管片-土体循环模型

3.1 轨道-盾构隧道循环模型

钢轨及轨道均采用欧拉梁单元建模，其中钢轨与轨道之间的扣件采用弹簧-粘滞阻尼进行模拟，轨道板与盾构管片通过弹簧-粘滞阻尼连接，同样，在钢轨及轨道的前后端节点为“共节点”，如图 2所示，左边的1 号节点为起始节点，右边的1号节点为一虚拟节点，其与左边的1号节点为共节点，结构形成闭环。

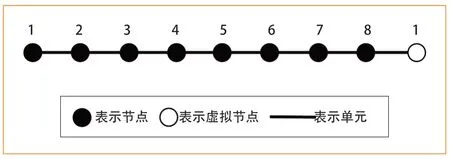
图2 循环结构模型

得到的轨道-盾构隧道循环模型的动力学方程为：

式（1）中，Mts和Kts为轨道-盾构循环隧道模型的质量和刚度矩阵；Cts为阻尼矩阵，通过瑞利阻尼获得；和Xts分别轨道-盾构循环隧道模型的加速度、速度和位移列阵；Fts为作用在轨道-盾构隧道循环模型的荷载列阵。

3.2 车辆模型

车辆模型采用多刚体-弹簧-阻尼系统进行仿真，其中每辆车包括1个车体、2个转向架和4个轮对。采用弹簧刚度和粘性阻尼对车体与转向架之间的悬挂系统（二系悬挂）和转向架与轮对之间的悬挂体系（一系悬挂）进行模拟，如图 3所示。图3中C表示车体；T1表示前构架；T2表示后构架；W1、W2、W3、W4表示同一节车厢的4个轮对；ky1和cy1分别表示一系悬挂横向刚度和阻尼；kz1和cz1分别表示一系悬挂垂向刚度和阻尼；ky2和cy2分别表示二系悬挂横向刚度和阻尼；kz2和cz2分别表示二系悬挂垂向刚度和阻尼；kx1表示一系悬挂纵向刚度；kx2表示二系悬挂纵向刚度；b1表示一系悬挂中2个竖向弹簧的水平距离之半；b2表示二系悬挂中2个竖向弹簧的水平距离之半；d1表示同1个转向架的2个轮对中心距离之半；d2表示同1个车箱的2个转向架中心距离之半；h1表示车体重心到二系悬挂横向弹簧的距离；h2表示转向架重心到二系悬挂横向弹簧的距离；h3表示转向架重心到一系悬挂横向弹簧的距离。

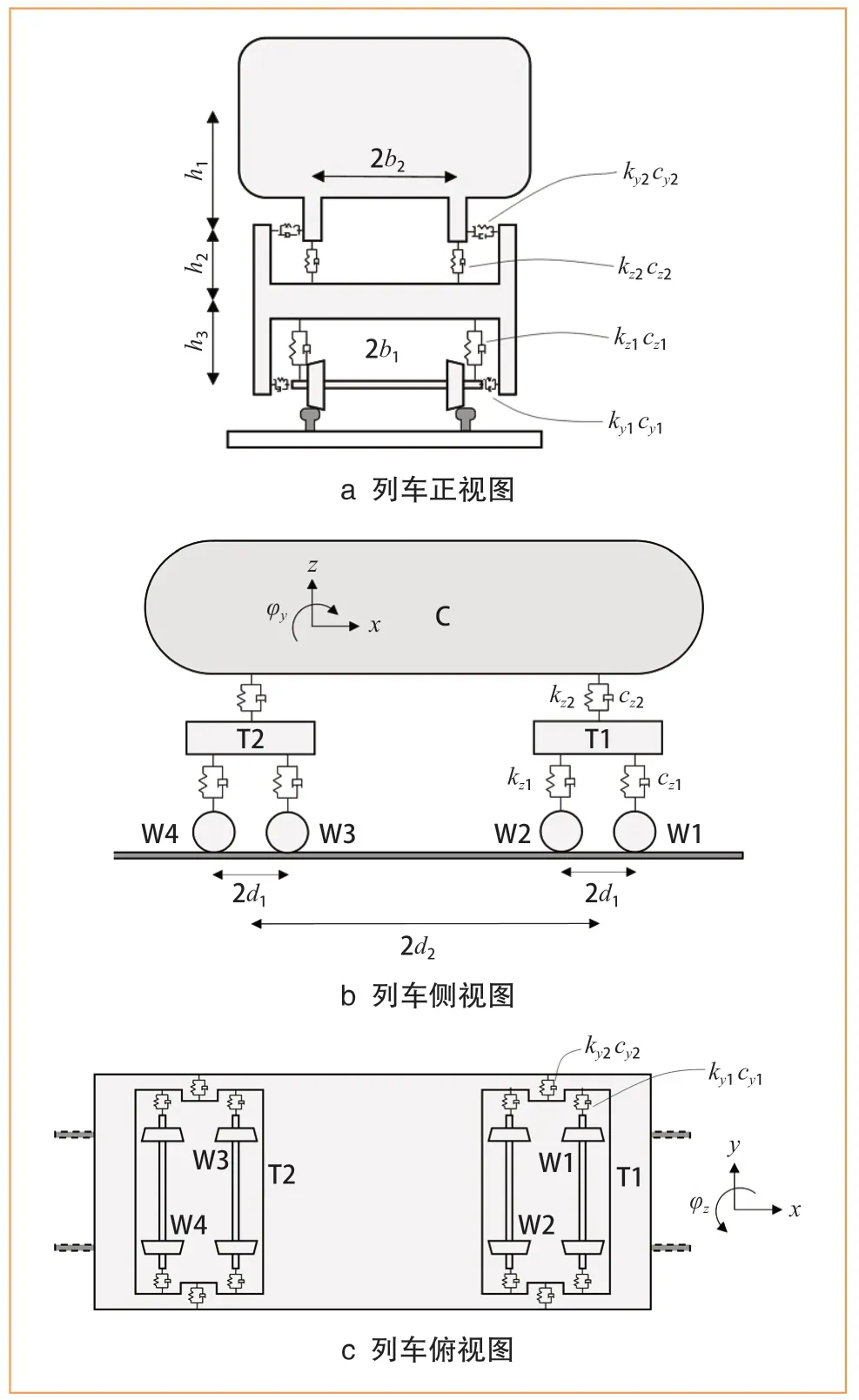
图3 车辆模型

根据弹性势能不变性原理，可以得到车辆的动力学方程为[9]：

式（2）中，Mv、Cv和Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵；Fv为荷载列阵；Xv为位移列阵。质量矩阵Mv的表达式如下：

式（3）中，n为列车节数；diag[ · ]表示对角矩阵；Mvi为第i节列车矩阵，其表达式为：

式（4）中，Mc、Mt和Mw分别为车体质量矩阵、构架质量矩阵和轮对质量矩阵，表达式分别为：

式（5）～（7）中，mc，mt，mw分别表示车体、构架及轮对质量；J表示转动惯量。

刚度矩阵的表达式如下：

其中，Kvi为第i节列车的刚度矩阵，其表达式如下：

式（9）中，Kt1w2为前构架与轮对的相互作用矩阵；Kt2w4为后构架与轮对的相互作用矩阵。

将车辆刚度矩阵中的刚度系数k全部替换为阻尼系数c，即可得到对应的阻尼矩阵。

3.3 系统动力学模型

列车模型和轨道-盾构隧道模型通过轮轨关系进行耦合，其中轮轨关系包含轮轨力和轮轨几何位移量2个方面，具体可见文献[9-12]。当车轮驶出图 2中的最右边的单元后，随即进入最左边单元，整个系统形成循环动力学模型。

4 算例

以长乐滨海快线机场站—中间风井区间盾构为例，有限元模型由土体、管片、轨道和钢轨4个部分组成，完整模型中土体选取长×宽×高= 1 500 m×100 m×40 m为计算土体，循环模型中土体选取长×宽×高=300 m×100 m×40 m为计算土体，土体共分为5个土层，自上而下分别为粉细砂、泥质粉细砂以及3个属性不一样的粉质黏土，粉细砂土层高5 m；泥质粉细砂土层高10 m；3个属性不一样的粉质黏土土层高分别为15 m、5 m、5 m，管片外径为8.3 m，内径为7.5 m，各部分的基本力学特性如表 1所示。列车采用常用的地铁列车型号，其关键参数如表 2所示。

表1 盾构管片-土体基本力学特性

表2 列车关键参数

4.1 模型验证

4.1.1 与已有文献结果对比

列车-轨道-结构系统是一个复杂的系统动力学模型，为验证该系统动力学模型计算结果的准确性，提取夏志强等人[3]的动力响应结果进行对比，该算例为6节编组AH型列车，车速为80 km/h，采用美国轨道谱生成轨道不平顺。对比结果如图4所示，可以看到，无论是钢轨位移时程或者垂向加速度时程响应，循环模型所得到的结果的幅值及趋势均与已有文献结果接近，论证了本文模型计算结果的准确性。

4.1.2 与完整模型的对比

循环模型中的结构-土体的矩阵维度与完整模型有较大差别，因此，也需要验证其计算结果的准确性。将完整模型作为精确解，通过对比这2种模型之间的响应，论证循环模型的准确性。图5为2种模型关键指标的动力时程响应，包含扣件处钢轨位移、车体垂向加速度和垂向轮轨力。可以看到，循环模型各个指标的计算的结果均与完整模型相吻合，证明了循环模型得到的结果与完整模型一致，从效率角度，完整模型的自由度数量约为循环模型的5倍。

图5 循环模型与完整模型对比验证

图6 不同车速下的车体加速度

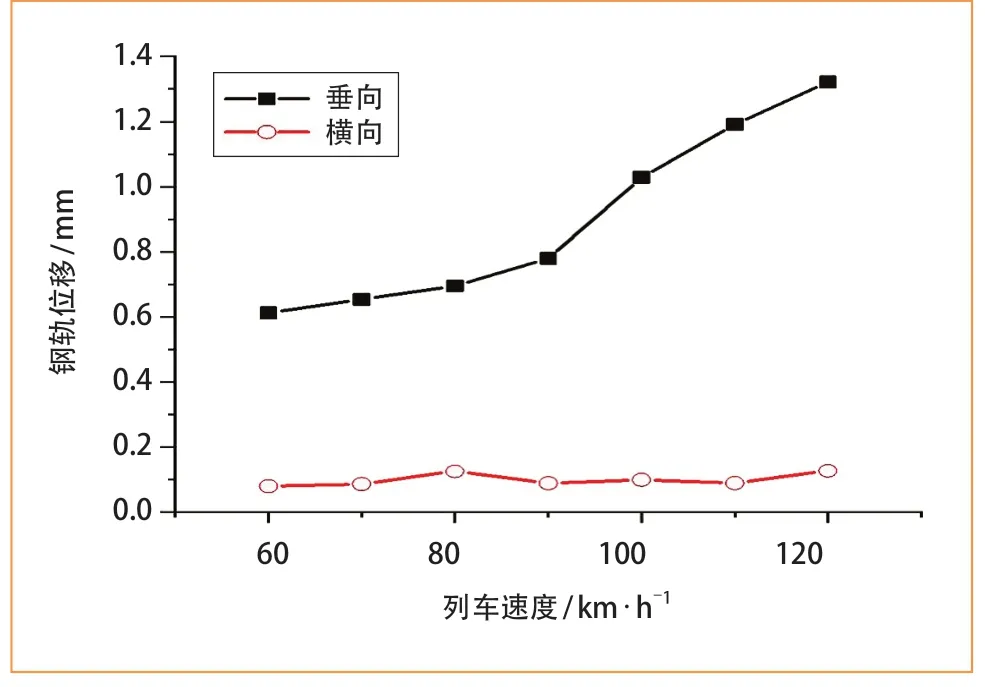
图7 不同车速下的钢轨位移

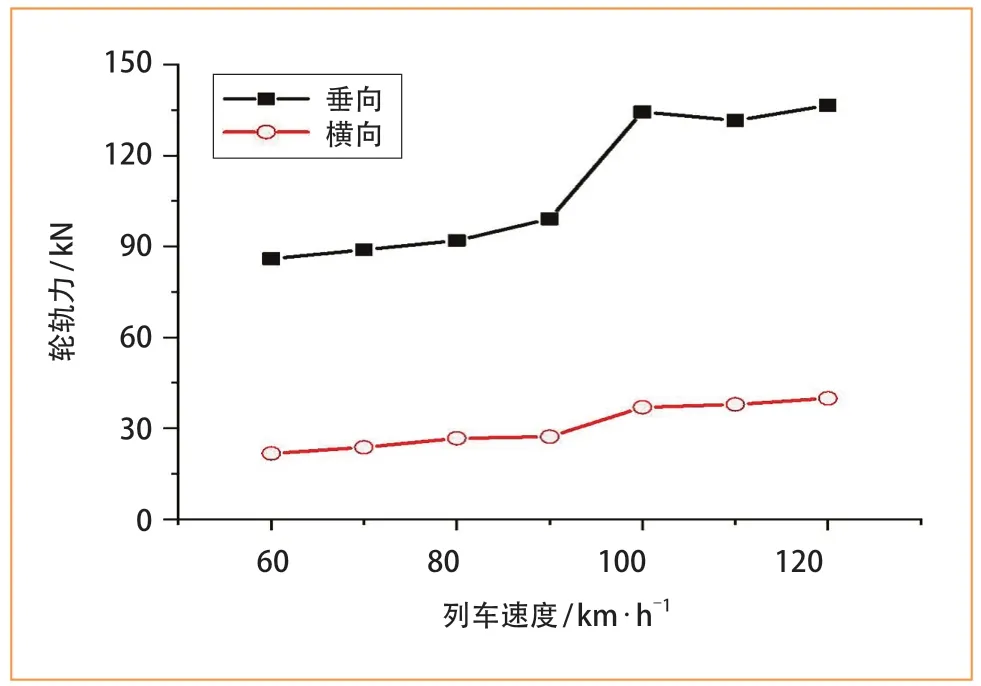
图8 不同车速下的轮轨力

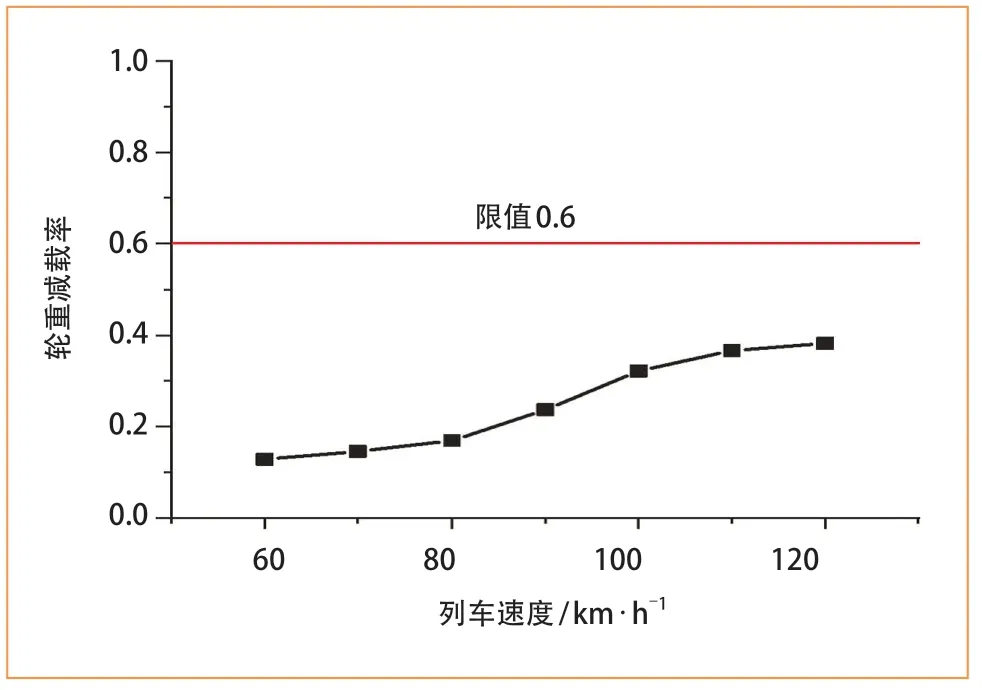
图9 不同车速下的轮重减载率

图10 不同车速下的脱轨系数

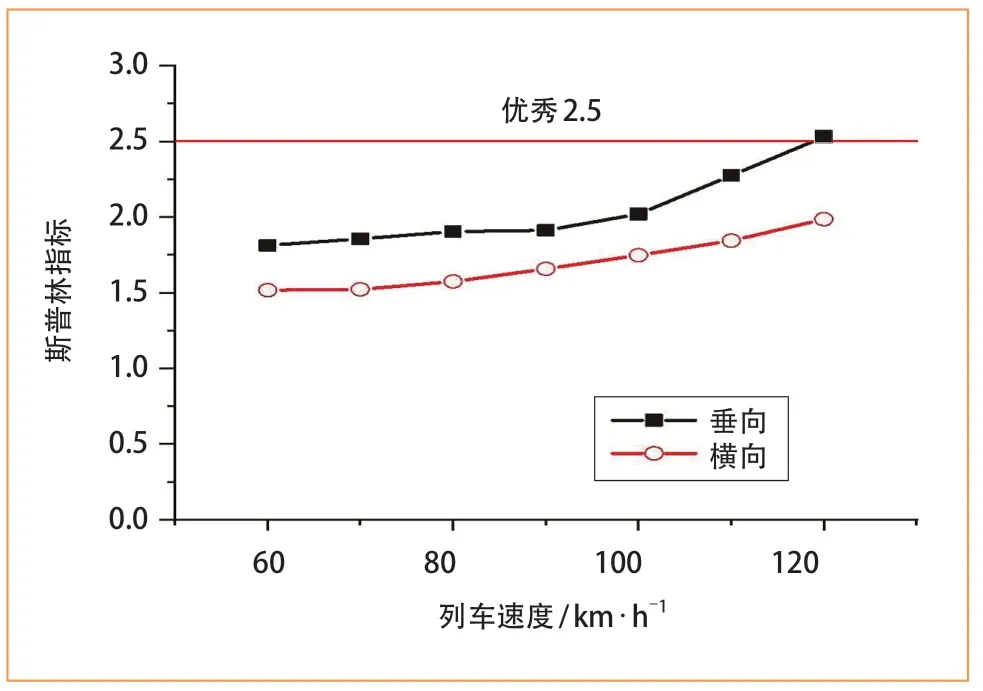
图11 不同车速下的平稳性指标

4.2 不同车速下的关键指标分析

为分析长乐滨海快线机场站—中间风井区间盾构段的地铁列车行车性能，基于循环模型对不同车速下的关键指标进行了计算，包含列车车体加速度、钢轨位移、轮轨力、轮重减载率、脱轨系数以及斯普林指标，其中轮轨力、轮重减载率、脱轨系数通常用于衡量列车的安全性能，车体加速度用于评价列车的舒适性，斯普林指标用于评价列车的平稳性。计算速度为60～120 km/h，涵盖了地铁列车的常用车速。

由图 6可以看出，车体加速度随着列车速度增大而增大，其中不同车速下垂向加速度均大于横向加速度，在列车的常用车速范围内，车体加速度均未超过行车振动的舒适性指标，即横向加速度1.0 m/s2、垂向加速度1.3 m/s2。

由图 7可以看出，钢轨在扣件处的垂向位移响应最大值随着车速增大而增大，钢轨横向位移对于车速变化不敏感，这是由于轮轨垂向力包含列车重力和轨道不平顺激励两部分，其中列车重力占主要部分，且造成的钢轨静态变形大，而横向力主要为轨道不平顺的激励，列车重力产生的比重较小，即造成的钢轨静态变形小，从而导致在不同车速下横向位移也很小。

由图 8可以看出，列车的轮轨力随着车速增大而增大，且垂向轮轨力的增大幅度大于横向轮轨力。

轮重减载是由于轨道不平顺激励导致轮轨垂向力动态浮动，减载率越大，说明其越不安全。由图 9可以看出，地铁列车的轮重减载率随着车速增大而增大，在计算车速即常用运营车速范围内，该指标未超限（限值为0.6）。脱轨系数是轮轨横向力与垂向力的比值，根据轮轨静态得到的限值为0.8，因此，在各国规范中也将0.8作为脱轨系数的限值。由图 10可以看出，脱轨系数随着车速增大而增大，在计算车速即常用运营车速范围内，该指标未超限。

斯普林指标是衡量列车振动过程平稳性的关键指标，在各国的铁路运营中广泛采用。斯普林指标越小，说明列车振动的平稳性越好，规范中将斯普林指标小于2.5定义为优秀。由图 11可以看出，列车的横向和垂向斯普林指标均随着车速增大而增大，其中垂向斯普林指标在不同车速下均大于横向斯普林指标，当车速小于120 km/h，列车的斯普林指标均为优秀，在车速为120 km/h时，斯普林指标略微超过优秀限值。总体而言，在正常运营车速范围内，地铁列车的各项动力学指标均为优秀或满足要求。

5 结语

分析地铁列车行驶性能时，建立大范围的盾构管片 -土体模型是必要的，但这对计算效率造成了严重影响。为解决这个问题，构建了一个列车-轨道-管片 -土体循环模型，并对该模型计算结果的准确性进行了验证。采用长乐滨海快线机场站—中间风井区间盾构区间作为工程背景，对地铁列车的行驶性能进行了深入分析，得出以下结论。

（1）使用循环模型能显著降低轨道-管片-土体的自由度数量，且其计算结果与完整模型一致。

（2）随着车速的增加，钢轨在扣件处的垂向位移响应最大值增大，但横向位移对车速的变化并不敏感。同时，列车的轮轨力也随车速的增加而增大，尤其是垂向轮轨力的增长幅度超过了横向轮轨力。

（3）列车车体的加速度随车速的增大而增大，其中不同车速下，垂向加速度总是大于横向加速度。同样地，列车的横向和垂向斯普林指标均随车速的增大而增大，而且在任何车速下，垂向斯普林指标都大于横向斯普林指标。

（4）地铁列车的轮重减载率和脱轨系数都随着车速的增加而增加。然而，列车行驶性能的所有动力学指标均符合规定要求。