Contact Angle Prediction Model for Underwater Oleophobic Surfaces Based on Multifractal Theory

Jiang Huayi; You Yanzhen; Hu Juan; Tian Dongmei; Qi Hongyuan;Sun Nana; Liu Mei(. College of Petroleum Engineering, Xi’an Shiyou University, Xi’an 70065, Shaanxi, China 2. Shaanxi Key Laboratory of Advanced Stimulation Technology for Oil & Gas Reservoirs, Xi’an Shiyou University, Xi’an 70065, Shaanxi, China . The Second Gas Production Plant, Changqing Oilfield Company, Yulin 79000, Shaanxi, China)

Abstract: Traditional microstructure scale parameters have difficulty describing the structure and distribution of a rough material’s surface morphology comprehensively and quantitatively. This study constructs hydrophilic and underwater oleophobic surfaces based on polyvinylidene fluoride (PVDF) using a chemical modification method, and the fractal dimension and multifractal spectrum are used to quantitatively characterize the microscopic morphology. A new contact angle prediction model for underwater oleophobic surfaces is established. The results show that the fractal dimension of the PVDF surface first increases and then decreases with the reaction time. The uniformity characterized by the multifractal spectrum was generally consistent with scanning electron microscope observations. The contact angle of water droplets on the PVDF surface is negatively correlated with the fractal dimension, and oil droplets in water are positively correlated.When the fractal dimension is 2.0975, the new contact angle prediction model has higher prediction accuracy. The maximum and minimum relative deviations of the contact angle between the theoretical and measured data are 18.20%and 0.72%, respectively. For water ring transportation, the larger the fractal dimension and spectral width of the material surface, the smaller the absolute value of the spectral difference, the stronger the hydrophilic and oleophobic properties, and the better the water ring transportation stability.

Key words: contact angle; hydrophilic-oleophobic surface; polyvinylidene fluoride; multifractal; prediction model

1 Introduction

The wetting phenomenon is the macroscopic result of the interaction of microscopic characteristics, such as the structural properties of the solid surface, the liquid properties, and the molecular force at the solid-liquid interface. Current research shows that the main factor affecting the wettability of a solid-liquid interface is the solid surface’s microscopic morphology, which is usually evaluated using surface roughness. However, the surface roughness is only a scale parameter and cannot accurately and comprehensively reflect the surface morphology[1].

Wenzel[2], Cassie, and Baxter[3]have conducted in-depth studies on the relationship between the micromorphology of solid surfaces and their wettability. They introduced the roughness factor and proposed the classical Wenzel and the Cassie-Baxter models[4]based on Young’s model.

However, a contact angle model based only on statistical parameters inevitably shows some deviations because of the different geometric morphologies and heterogeneity of real material surfaces. Also, existing contact angle prediction models are based on only a few studies of oilwater two-phase liquids. This point is crucial for water ring stability in heavy oil transportation by water rings[5-7].Therefore, finding evaluation parameters unrelated to the scale and establishing a more accurate contact angle prediction model for the microscopic morphology of underwater oleophobic surfaces is necessary to comprehensively and quantitatively study the relationship between microscopic morphology and wettability.

Mandelbrot first created fractal theory and proposed the fractal dimension to quantify the complexity of irregular objects in the 1970s[8-9]. Yang[10]proposed that fractal theory could be used to describe the microscopic geometric characteristics of solid surfaces qualitatively.Using fractal theory, Yuan et al.[11]established a surface contour mathematical model that provides a theoretical basis for exploring the characterization parameters of three-dimensional surface morphologies. Because there is a certain degree of self-similarity between the local and global surface contour curves, the microscopic morphology of a solid surface can be characterized by a fractal dimension[8,9,12-14].

Huo et al.[15]investigated the surface morphology of Ti-Mg supported polyethylene particles and catalysts using scanning electron microscopy (SEM). They found that the two surfaces had prominent fractal characteristics and that it was feasible to characterize the surface by a fractal dimension. Soumya et al.[16]prepared nanosized molybdenum oxide (MoO3) films by changing the ablation time and annealing temperature after deposition and analyzed their surface fractal characteristics. The results showed that the surface roughness decreased with increasing fractal dimension, consistent with atomic force microscopy analysis.

Researchers worldwide have improved classical wetting models to further explore the relationship between fractal parameters and contact angle. Zeng[17]established a mathematical fractal dimension and scale model under the Wenzel state, linking the apparent and Young’s contact angles. The model was verified by the water wetting experimental results of a nanoscale fractal surface reported in the literature. Based on fractal theory, Jiang et al.[18]established a new model for calculating the contact angle of water droplets under the Cassie-Baxter state, as follows:

whereθfis the actual contact angle,φsandφvrepresent the area fractions of the solid-liquid and gas-liquid interfaces, respectively, andφs+φv=1.Lrepresents the upper limit scale of the fractal surface, andlrepresents the lower limit scale.Dis the fractal dimension, andθeis the intrinsic contact angle. The simulated data of the model are basically consistent with measured water contact angle data on a superhydrophobic surface with a nanoscale silicon carbide microstructure. Jain et al.[19]used the Weierstras-Mandelbrot (W-M) function rough fractal model to describe a multiscale random rough surface. On this basis, they proposed a mathematical model to evaluate the apparent contact angles on different wettability surfaces as follows:

whereθis the equilibrium contact angle under the Cassie state,r1is the roughness ratio of the surface wetting area,φis the area fraction of the solid area wetted by liquid,andθ0is the intrinsic contact angle. For a surface having a fractal structure, the Wenzel contact angle prediction model of a surface with a fractal structure can be obtained by approximating the roughness factorras (L/l)D-2[20]:

whereθwis the actual contact angle, θ is the intrinsic contact angle in the Wenzel contact angle prediction model, (L/l)D-2represents the roughness factor,Lis the upper limit scale of the fractal surface, andlis the lower limit scale. For an actual random fractal surface,the maximum and minimum peaksZmaxandZminof the contour curve can be used to replace the upper and lower limit scalesLandlof the fractal surface, and Eq. (3)becomes

Thus, although many investigators introduce fractal theory to study the influence of fractal dimension on contact angle and obtain contact angle prediction models,a single fractal dimension has difficulty comprehensively and quantitatively describing the structure, distribution,and other surface morphology details[21]. Therefore, it is necessary to seek other parameters to characterize the microscopic morphology of a single fractal to obtain a new contact angle prediction model based on fractal theory and improve the contact angle prediction accuracy for fractal structure surfaces.

A multifractal is a singular set of non-uniform fractal dimension distributions superimposed with subsets of different fractal characteristics. It is necessary to introduce its probability distribution function and calculate its moments to form a continuous fractal dimension spectrum, called a multifractal spectrum, to describe the complexity and nonuniformity of a fractal in more detail. Mwema et al.[22]prepared thin films at substrate temperatures of 44.5–100 °C and proposed a multifractal method to characterize the microscopic morphology of thin films. Shan et al.[23]used SEM to observe the microscopic morphology of copolymer hydrogel samples and introduced the multifractal spectrum. The results showed that the multifractal spectrum, singular index α,and Hausdorff dimension could quantitatively characterize the inhomogeneity and network distribution width of hydrogel homopolymers and copolymers.

Jiang et al.[1]constructed the microscopic morphology of different steel surfaces and calculated the fractal parameters by adjusting the chemical etching time. Their results showed that a fractal dimension and multifractal spectrum can characterize the surface morphology of the material.The contact angle increased with increasing fractal dimension. Therefore, although a multifractal can be used to supplement the quantitative description of the surface morphology of materials, few studies have introduced multifractals into contact angle prediction models.

Given this, polyvinylidene fluoride (PVDF) material was studied in this paper and was modified to a hydrophilic underwater oleophobic surface. The microscopic morphology of the surface was comprehensively and quantitatively described by combining the fractal dimension and multifractal spectrum to establish a new contact angle prediction model for underwater oleophobic surfaces. This study has important guiding significance for regulating water ring stability, and the new contact angle prediction model established has essential application value in fields such as liquid transportation, aerospace,biomimetic films, and coatings.

2 Fractal Theory and Contact Angle Prediction Model

2.1 Fractal theory

2.1.1 Fractal dimension

This paper uses the fractal dimensionDto describe the fractal characteristics of a material surface morphology quantitatively. The box-counting dimension is chosen to calculate the fractal dimension using MATLAB.

N(ε) is the number of sets whose diameter isεin the cover fractal set A, with the following mathematical relationship:

Taking lg(ε) as the abscissa and lg(N(ε)) as the ordinate,a straight line is fitted in double logarithmic coordinates.The negative of the slopekis the box-counting dimension.

2.1.2 Multifractal

This paper uses a multifractal spectrum to describe the fractal characteristics of a material’s surface morphology quantitatively. A multifractal spectrum is usually characterized by two parameters: the spectral width Δαand the spectral difference Δf(α).

In the box-counting method of multifractal theory, the fractal image is covered by a square box with edge lengthε,nijrepresenting the number of fractal pixels in box (i,j),with Σnijrepresenting the number of pixels of all fractal numbers. The probability measurePij(ε) of the fractal image in eachε×εbox is defined as

The probability measurePij(ε) in the scale-free selfsimilar region can be written as

whereαijis the dimension of the fractal image in the box,called the local fractal dimension, also known as the singularity index.

Then, Δα=αmax-αmindefines the disorder of the overall fractal region’s probability measure and the complexity of the surface. A larger Δαrepresents lower surface uniformity.

The dimension functionf(α) is defined as a subset of the singular indexα:

The complexity and irregularity of the surface are mainly presented as Δf(α)=f(αmin)-f(αmax).

Because there is a unique one-to-one correspondence betweenαandf(α), there is a dimension spectrum describing multifractal properties called the multifractal spectrum.

The sum ofqsquares ofPij(ε) can be expressed by the partition functionχq(ε). Then the relationship between τ(q) andqis

where τ(q) is the mass index, andqis the weighting factor. If τ(q) is linear withq, the graph is single-fractal.If τ(q) is a convex function ofq, the graph is multifractal.A Legendre transformation of Eqs. (8) and (9) can be obtained as[24]

In summary, a multifractal spectrum is usually characterized by a spectral width Δα and spectral difference Δf(α):

where αmaxandf(αmax) are the maximum probability subset dimension and the sum of the maximum probability subset dimensions, respectively, andαminandf(αmin) are the minimum probability subset dimension and the sum of the minimum probability subset dimensions, respectively.The spectral width Δαcharacterizes the uniformity of the probability distribution. The smaller the Δα, the more uniform the distribution. The spectral difference Δf(α) characterizes the difference between the sum of the minimum and the maximum probability subset dimensions.When Δf(α) > 0, the multifractal spectrum is left-hooked,and the surface morphology height is relatively low. When Δf(α) < 0, the multifractal spectrum is right-hooked, and the surface morphology height is relatively high.

The singularity index α and multifractal spectrumf(α) are calculated by first importing a captured SEM image into the current MATLAB folder and processing the SEM gray image into a binary image. The box-counting method is used to calculate the fractal dimension with a computer program according to Eq. (11). Finally, the spectral width Δαand spectral difference Δf(α) are calculated according to Eqs. (12) and (13).

2.2 Contact angle prediction model

Previous studies have found that a single fractal dimension cannot fully and accurately characterize a surface’s morphology. Therefore, this paper introduces a multifractal spectrum based on a single fractal dimension to reasonably optimize Eq. (4) to improve the accuracy of the contact angle prediction model.

Through linear fitting analysis, it is found that there is a particular mathematical relationship between (Zmax/Zmin) andTherefore, for the actual random fractal surface, this paper introduces the multifractal spectrum parameters into Eq. (4) to obtain a contact angle prediction model for an underwater oleophobic surface:

where θ0is the intrinsic contact angle of oil droplets in water on a smooth surface. In this paper, the contact angle measured between the smooth specimen surface after uniform grinding (using 2000 mesh, 3000 mesh,5000 mesh, and 7000 mesh sandpapers, in that order)and oil droplets in water is used as the intrinsic contact angle. It can be seen from Eq. (14) that cosθwincreases with increasingand fractal dimensionDwhen the tested material surface is underwater oleophilic. Therefore,θwdecreases as they increase,making the surface more oleophilic. By contrast, when the tested material surface is underwater oleophobic,cosθwdecreases with increasingand fractal dimensionD, soθwincreases as they increase, making the surface more oleophobic. In other words, for the measured surface, the degree of underwater oleophobicity/oleophilicity increases with increasingand fractal dimensionD.

For water-annulus transportation, a pipe wall with underwater oleophobicity can be adjusted by changing its surface morphology, that is, by increasing the fractal dimensionDand spectral width Δαand decreasing the absolute value of spectral difference Δf(α). Thus, oil has difficulty spreading on the pipe wall surface, and the waterannulus transportation stability is noticeably improved.

3 Experimental Verification Method of Model

3.1 Preparation of microscopic morphology of PVDF surface

It was found that chitosan and nano-silica have good hydrophilicity. In this paper, chitosan is modified by the reaction of glutaraldehyde and silica with the amino and carboxyl groups of chitosan, respectively. Chitosansilica composites with different microstructures were prepared on the surface of PVDF specimens by changing the reaction timet. In addition, PVDF specimens with hydrophilic underwater oleophobic properties were obtained. It is worth noting that the chemical modification method used in this article has good durability.The specific experimental steps are as follows:

(1) The PVDF specimen was cut into 15 mm×10 mm×2 mm pieces. A 1.25 mol/L sodium hydroxide alcohol solution was prepared with a 1:1 volume ratio of anhydrous ethanol to distilled water. The specimen was placed in the sodium hydroxide alcohol solution for 1 min at a water bath temperature of 75°C. After that, the specimen was cleaned with ethanol and dried at room temperature.

(2) A 2 g oxalic acid was dissolved into 80 mL distilled water. The solution was ultrasonically dissolved uniformly for 15 min. Subsequently, 2 g chitosan powder was added and stirred at 50°C until completely dissolved.(3) Deionized water and anhydrous ethanol were mixed with a volume ratio of 25 mL: 125 mL. The solution was ultrasonically mixed uniformly for 15 min. Then, a 4 mL 35% ammonia solution was added and ultrasonically remixed for 15 min. Subsequently, a 0.2 mL tetraethyl orthosilicate was added slowly and mixed by magnetic stirring for 24 h.

(4) The prepared chitosan and silica solution were mixed at a volume ratio of 50 mL: 50 mL and magnetically stirred for 2 h. Then, a 0.15 mL glutaraldehyde solution was added and magnetically stirred for 12 h to obtain the chitosan-silica solution.

(5) The PVDF specimens pretreated by step (1) were placed in the chitosan-silica solution and were removed after standing for 3, 5, 7, 9, 11, 13, 15, 17, and 19 min,respectively, and then dried at room temperature. The treated PVDF specimens were then placed in 0.1 mol/L sodium hydroxide solution and removed after standing for 30 min. Finally, they were cleaned with distilled water and dried at room temperature.

Because the PVDF specimens were not conductive, a Q150RES automatic ion sputtering instrument was used to spray them with gold, and a JSM-6390A scanning electron microscope was used to obtain the surface morphology of the PVDF specimens.

3.2 Measurement of contact angle on the underwater oleophobic surface

A liquid-liquid-solid contact angle measurement device was designed to measure the contact angle of oil droplets in water on the specimen surface. The measurement device includes an end cover, cavity, sampling platform,and adjusting base. A schematic diagram of the device is shown in Figure 1. Gasoline and diesel were selected as the tested oil droplets. The oil droplet volume was 3 μL and was precisely controlled by a microsyringe.

Figure 1 Schematic diagram of contact angle measurement of oil droplets in water

The specific measurement procedure steps are as follows:(1) Fix the PVDF specimen on the lower surface of the sampling platform with two elastic tablets. Adjust the base’s height to keep the sampling platform’s lower surface at the same height as the lens center of the contact angle measurement device.

(2) Open the end cover, filling the cavity with distilled water to overwhelm the sampling platform’s lower surface. Screw on the end cover to seal the cavity.

(3) Fix the contact angle measurement device for oil droplets in water on the rotating platform of a JC2000D1 contact angle meter and ensure that no movement occurs.

(4) Add 3 μL gasoline or diesel to the microinjection pump and set the injection parameters. Drop the tested oil droplets onto the specimen’s center through the microinjection needle.

(5) Obtain the contact angle image of oil droplets in water using the JC2000D1 contact angle meter camera and calculate the contact angle.

4 Results and Discussion

4.1 SEM at different reaction times

Hydrophilic and oleophobic surfaces with different morphologies were prepared by controlling the reaction time between the PVDF specimens and the chitosansilica solution. The surface morphologies of the PVDF specimens were collected by the scanning electron microscope using 400× magnification. The results are shown in Figure 2.

Figure 2 Morphologies of PVDF surfaces for different reaction times

Figure 2 shows that the microscopic surface morphology of the pretreated-only PVDF specimen is unchanged.The specimen surface is not rough, and it is the flattest specimen. When the reaction time is 3–7 min, many upward curling structures appear on the specimen surfaces. With increased reaction time, the number of upward-curling structures gradually decreases, but their sizes increase, possibly because the chitosan-silica coats the PVDF specimen surface. However, the coating is incomplete because of the shorter reaction time.

A few block bumps appear on the surface whent=9 min andt= 11 min. Whent= 13 min, the PVDF specimen surface is composed of a crawler structure. This phenomenon may be because glutaraldehyde smoothes the chitosan-silica film coated on the PVDF specimen surface with the extended reaction time. Whentincreases to 15–19 min, the edge of the crawler structure on the surfaces gradually rolls up and then slowly disappears.This change may be because the chitosan-silica film gradually peels from the surface with the continuously extended reaction time, making the surface roughness structure disappear and decreasing the roughness.

4.2 Fractal dimension and multifractal spectrum

This paper uses the fractal dimension and multifractal spectrum to comprehensively and quantitatively characterize the surface morphology of materials. The multifractal spectrum includes the spectral width Δα and spectral difference Δf(α).

The fractal dimensions of PVDF at different reaction times are shown in Figure 3. The multifractal spectrum of PVDF is shown in Figure 4.

Figure 3 Variation of PVDF fractal dimension with reaction time

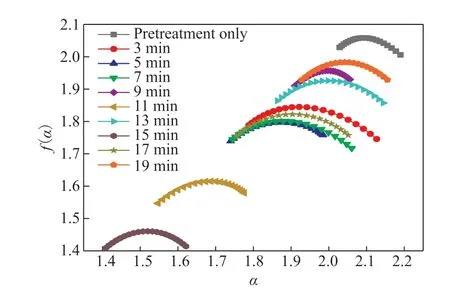
Figure 4 PVDF multifractal spectrum

According to the definitions of the spectral width and spectral difference, the PVDF multifractal spectrum parameters Δα and Δf(α) were calculated from Figure 4,and the results are shown in Table 1.

Table 1 PVDF multifractal spectrum parameters at different reaction times

It can be seen from Figure 3 that the fractal dimensions of the PVDF specimen surfaces are greater than 2, indicating that they have apparent fractal characteristics[25]. With increasing reaction time, the fractal dimension of PVDF first increase and then decrease, reaching a maximum value of 2.0986 att= 13 min. This is because the PVDF specimen surface initially exhibits many upward-curling structures, followed by the disappearance of the upward-curling structures to form a crawler structure. Finally, the crawler structure disappears, and the specimen surface becomes flat again.

Whent= 17 min, the fractal dimension of the PVDF specimen surface increases slightly and is 0.096% higher than that att= 15 min, consistent with the microscopic morphology of the corresponding sample in Figure 2. In addition, according to the calculations, the spectral width of PVDF specimen surface att= 17 min also increases by 39.80% compared with that att= 15 min, indicating that the surface morphology of the PVDF specimen is more uneven att= 17 min. This also describes the material’s surface morphology from the perspective of the multifractal spectrum parameter.

Table 1 shows that the uniformity of the PVDF specimen surface characterized by the spectrum width Δα is consistent with the SEM observation results.The spectrum width att= 9 min decreases by 40.53%compared tot= 5 min. However, the corresponding fractal dimension increases by 0.39%. The results for the spectral difference Δf(α) show they were less than zero att= 9 min andt= 5 min, and the multifractal spectrumshows a right hook shape. According to the definition of Δf(α), the number of maximum probability subset dimensions is greater than the number of minimum probability subset dimensions. That is, the large-scale microstructure of the PVDF specimen surface occupies a large proportion, possibly because the upward curling structure of the PVDF specimen surface disappears at this time, leaving only a few granular protrusions.

It is apparent that the single fractal dimension cannot fully and accurately characterize the microscopic morphology,so it is necessary to combine multifractal spectrum parameters. The spectrum width att= 15 min is 7.35%lower than att= 11 min, and the corresponding fractal dimension is also reduced by 0.51%. This phenomenon may be because the surface roughness of the PVDF specimen is less fort= 15 min, so the roughness is reduced, and the overall microscopic morphology is more uniform than fort= 11 min. This approach gives a more complete description of the microscopic morphology of the material surface.

4.3 Influence of fractal parameters on contact angle

The contact angles of water droplets and gasoline and diesel droplets in water on PVDF specimens for different reaction times are shown in Figure 5.

Figure 5 Contact angles of different droplets on PVDF specimens for different reaction times

It can be seen from Figure 5 that when the reaction time of the PVDF specimen is 5–17 min, the specimen surfaces exhibit hydrophilic and underwater oleophobic states. However, the pretreated-only specimen surface displays hydrophobic and underwater oleophobic states.Moreover, for most of the reaction times, the contact angles of gasoline droplets in water on specimen surfaces are smaller than those of diesel droplets in water. This difference may be due to the fact that the surface tension of gasoline is about 22 mN/m and diesel is about 26.8 mN/m[26], which is consistent with the fact that the contact angle of liquid increases with increasing surface tension for the same solid surface. Whent= 13 min, the contact angles of water droplets on the specimen surface have a minimum value of 52.3°. In this case, distilled water can wet the surface of the PVDF specimen well and can readily spread on it. Whent= 11 min, the maximum contact angles of gasoline and diesel droplets in water on PVDF specimens are 137.5° and 138.3°, respectively,showing that oil droplets can hardly wet the surface of the PVDF specimen. That is, oil has difficulty adhering to the PVDF wall during water ring transportation, while the water film can firmly adhere to the PVDF wall, allowing the water ring to achieve the most stable state.

A scatter diagram of the contact angles of water droplets and gasoline and diesel droplets in water and the fractal dimension of the PVDF specimen surface are provided in Figure 6.

Figure 6 Relationship between the surface fractal dimensions of PVDF specimens and the contact angles of water droplets and gasoline and diesel droplets in water

Figure 6 shows that the contact angles of water droplets on the specimen surfaces decrease with increasing surface fractal dimension and have a significant negative correlation. The contact angles of gasoline and diesel droplets in water increase with increasing surface fractal dimension, and there is a significant positive correlation between them. Overall, it is consistent with the law that the rougher the surface of lyophilic (lyophobic) materials,the larger the fractal dimension and the more lyophilic(lyophobic) the surface[25]. When the fractal dimension reaches its minimum value of 2.0672, the measured contact angles of water droplets on the PVDF surface reach their maximum value of 94.4°. This may be because the pretreated PVDF specimen surface is smooth and has no rough structure, so the fractal dimension achieves a minimum value.

Because the contact angle increases with decreasing fractal dimension[27], the measured value of the water droplet contact angle is the smallest for the largest fractal dimension, and vice versa. When the fractal dimension reaches a larger value of 2.0975, the measured contact angles of gasoline and diesel droplets in water reach their maximum values of 137.5° and 138.3°, respectively.When the fractal dimension reaches the maximum value of 2.0986, the measured contact angles are 129.5° and 125.5°, respectively. For fractal dimensionD, a value of 2.0975 is only 0.052% smaller than 2.0986, but the contact angle of gasoline and diesel droplets in water increase by 6.18% and 10.17%, respectively. From Table 1, it can be seen that the reason for the large difference in contact angle for similar fractal dimensions may be that the spectrum width atD= 2.0975 decreases by 18.53% compared to atD= 2.0986. That is, the specimen surface is more uniform atD= 2.0975. These results also supplement the description of fractal dimension from the perspective of multifractal spectrum parameters.

Therefore, it can be concluded that for water ring transportation, the larger the fractal dimension of the material surface, the smaller the contact angle of water droplets and the larger the contact angle of oil droplets in water, making the hydrophilic-oleophobic properties of the pipe wall stronger, and the water ring stability better.

4.4 Verification of contact angle prediction model

In this section, Eqs. (4) and (14) are used to calculate the contact angles of PVDF specimens with different fractal dimensions. The relative deviations between the calculated and measured contact angles before and after optimization are compared to further verify the prediction accuracy of the new mathematical model. The results are shown in Figure 7. The intrinsic contact angles from Eqs. (4) and (14) are 111.61° (gasoline droplet in water)and 112.30° (diesel droplet in water). In Eq. (4), the maximumZmaxand the minimumZminof the contour curve are calculated by a computer program. The spectral width Δα and spectral difference Δf(α) in Eq. (14) are shown in Table 1.

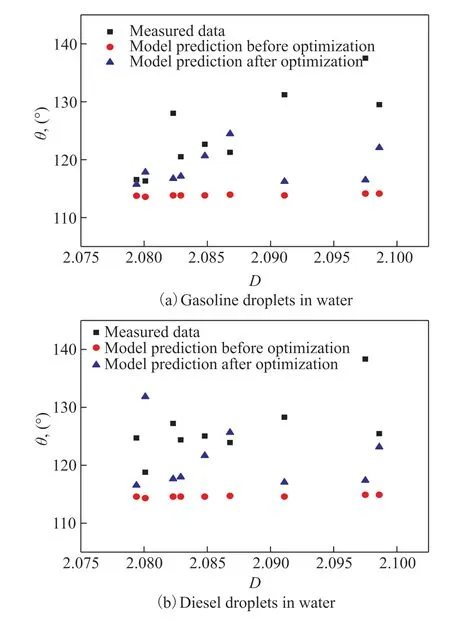
Figure 7 Comparison of measured and theoretical data for oil droplet contact angles in water on PVDF specimen surfaces

It can be seen from Figure 7 that the theoretical contact angles of oil droplets in water after optimization are closer to the measured data than those before optimization. In combination with Figure 6, it can be seen that for the PVDF specimens, the maximum standard deviation of the measured contact angles of gasoline droplets in water is 4.94, and the minimum is 1.62. The maximum standard deviation for diesel droplets in water is 4.62, and the minimum is 1.37. The standard deviation of the measured contact angles on the material’s surface is less than 5. The measured results are more accurate and have practical significance.

The theoretical data for the contact angles of oil droplets in water after optimization on PVDF specimens differ significantly from those before optimization. WhenD= 2.0868, the difference between the theoretical contact angle of gasoline droplets in water before and after optimization is largest at 10.5°. For diesel droplets in water, whenD= 2.0801, the difference between the theoretical values before and after optimization is largest at 17.5°. The maximum relative deviation of the contact angle between the theoretical data obtained from the new prediction model and the measured data is 18.20%, and the minimum relative deviation is 0.72%.

The average, maximum, and minimum relative deviations after optimization are generally reduced compared with those before optimization. Among them, the average relative deviation of contact angles of gasoline droplets in water on PVDF specimen surfaces is reduced by 1.40%,and the average relative deviation of gasoline droplets in water is reduced by 2.39%. These reductions indicate that the new contact angle prediction model improves the calculation accuracy for the contact angle of oil droplets in water. For water ring transportation, the fractal dimensionDand spectral width Δα can be increased, and the absolute value of the spectral difference Δf(α) can be reduced by changing the pipe wall’s surface morphology.Thus the pipe wall has underwater oleophobic wetting characteristics, meaning that the oil has difficulty spreading on the pipe wall surface, which improves the water ring transportation stability.

5 Conclusions

In this paper, hydrophilic and underwater oleophobic PVDF surfaces with different morphologies were prepared by changing the reaction time. The fractal parameters were used to characterize the surface morphology of the PVDF and were calculated using MATLAB. The influence of the fractal parameters on the contact angle was analyzed. Finally, a new contact angle prediction model with higher accuracy for underwater oleophobic surfaces was obtained by optimization.

The findings of this study are summarized as follows:(1) The fractal dimension of the PVDF surface first increases and then decreases with the reaction time,reaching a maximum value of 2.0986 at 13 min. The spectral difference Δf(α) and spectral width Δα describe the PVDF surface morphology and are consistent with observations from SEM images.

(2) The contact angle of water droplets on the PVDF surface decreases, and the contact angle of oil droplets in water increases with increasing fractal dimension.WhenD= 2.0975, the measured contact angles of water droplets on the PVDF surface reach a minimum value of 57.3°, and oil droplets in water reach a maximum value of 138.3°.

(3) An existing contact angle prediction model was optimized by introducing Δα and Δf(α). After optimization, the maximum and minimum relative deviations between the theoretical and measured data are 18.20% and 0.72%, respectively. For water ring transportation, the surface morphology of the pipe can be changed to increase the fractal dimension and spectral width and decrease the absolute value of the spectral difference. This change gives the pipe wall hydrophilic and underwater oleophobic wetting characteristics,enhancing the stability and efficiency of water ring transportation.

Acknowledgements:This work was supported by the Natural Science Basic Research Program of Shaanxi (Program No.2023-JC-YB-351), the Scientific Research Program Funded by the Shaanxi Provincial Education Department (Program No. 20JS118), and the Xi’an Shiyou University Graduate Innovation and Practice Ability Training Plan (YCS21212097,YCS21212092).