磁悬浮系统的相位超前校正控制器设计
2023-10-23蓝昕雨钟志贤李先瑄陈金华
蓝昕雨,钟志贤,李先瑄,陈金华
(桂林理工大学 机械与控制工程学院,广西 桂林 541006)
0 引 言
磁悬浮系统在许多领域都具有很强的实用性[1-5], 在医学上可用作磁悬浮人工心脏泵、 在机床中可用于超高速铣削、 在计算机领域中可作为硬盘光盘转子支撑、 在石油与天然气工业中被应用于低温涡轮膨胀机等, 随着磁悬浮及控制技术的发展, 磁悬浮系统的应用越来越广泛。
在实际的磁悬浮控制系统中, 时滞是不可避免的, 并且该问题会严重影响磁悬浮控制系统的稳定性[6]。针对磁悬浮系统的时滞问题, 众多学者做了许多研究工作[7-10]。Soni等[11]采用帕德近似法对磁悬浮系统反馈信号的时滞值作线性逼近, 通过有时滞的数值模拟验证动力学模型的稳定性, 为时滞磁悬浮系统的应用提供了思路。Sun等[12]构建了具有时滞补偿的滑模面, 采用双层神经网络及自适应方法线性逼近, 提出了有限时间自适应跟踪控制器, 利用李雅普诺夫法验证了所提控制器的有效性, 为时滞磁悬浮系统控制器的深入研究提供了理论依据, 并在文献[13]中针对磁悬浮系统的时滞问题提出了基于黎卡提法与滑模控制相结合的自适应鲁棒控制器, 通过仿真和实验表明所提方法能够有效抑制磁悬浮系统的时滞。郑凯[14]建立了磁悬浮系统的时滞动力学模型, 并使用时滞控制律设计了镇定控制器, 使磁悬浮系统的时滞得到了有效抑制。
以上方法从控制系统建模和控制器设计两方面推进了磁悬浮控制系统时滞的研究进程, 但存在着如下问题: 1)控制算法过于复杂且部分控制算法依赖于精确的数学模型, 难以应用于实际的控制系统; 2)对磁悬浮系统的时滞等不确定性加以描述后, 基于模型设计的控制器的阶数会增加, 控制效果难以符合预期设定。
针对以上问题, 本文将相位超前控制方法应用于磁悬浮球系统。相位超前控制方法是控制系统中用于修正系统伯德图的手段, 其优点是能根据不同系统的伯德图设置不同的参数, 在不变更系统幅值的条件下减弱系统相位的滞后, 无须提高控制器的阶数就能获得良好的控制效果。除此之外, 相位超前校正具有抑振的特点[15-16]。基于此, 首先建立单自由度磁悬浮系统的数学模型, 然后根据磁悬浮系统的相位裕度设计相位超前校正控制器, 进而采用伯德图与奈奎斯特图验证相位超前校正控制器的稳定性, 最后开展了仿真分析和悬浮实验研究, 以期设计出具有响应速度快、 抖振小的相位超前控制器等。
1 磁悬浮球系统的数学模型
由图1所示, 磁悬浮实验系统由钢球、 电磁绕组、 功率放大器、 激光传感器、 驱动电路以及上位机构成。磁悬浮球系统的传递函数为

图1 磁悬浮系统结构图[17]Fig.1 Structure diagram of magnetic levitation system
(1)
式中: 系数A=i0/2g;g为重力加速度, m/s2; 系数B=i0/x0;i0表示平衡电流, A;x0表示钢球处于平衡状态时钢球质心与电磁铁磁极间的气隙, mm;Ka代表功率放大器的增益[17]。
磁悬浮球系统的物理参数如表1所示。
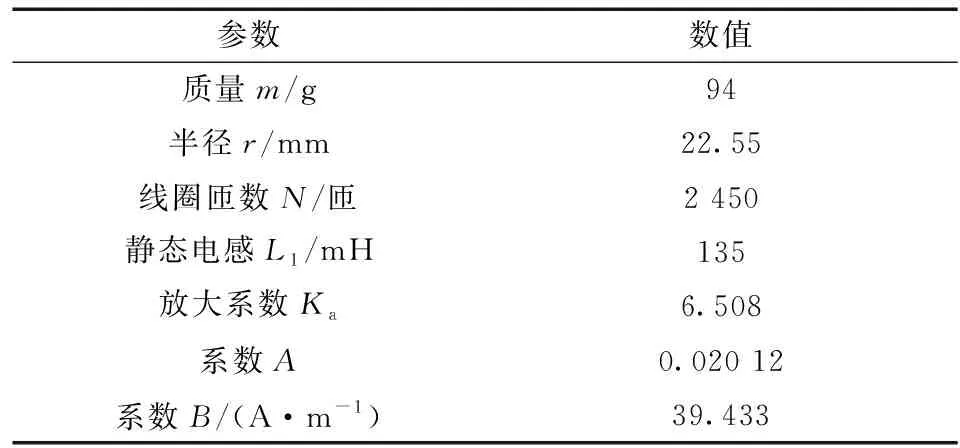
表1 磁悬浮球各项物理参数
将表1中的物理参数代入式(1), 得到单自由度磁悬浮系统的传递函数如下:
(2)
2 相位超前校正控制器的设计
磁悬浮闭环控制系统的方框图如图2所示。其中, 被控系统G0(s)的伯德图如图3a。设校正后的磁悬浮系统的相位裕度为50°, 稳态误差系数Kp为5。由于相位超前校正控制会让系统产生幅值衰减的影响, 故串联放大倍数为Kc的功率补偿放大器来消除此影响, 则相位超前校正控制器

图2 校正后的磁悬浮闭环控制系统框图Fig.2 Block diagram of corrected magnetic suspension closed-loop control system

图3 磁悬浮系统的伯德图Fig.3 Bode diagrams of magnetic levitation system
(3)
计算出式(3)中的增益Kcα, 根据初始设定的稳态误差, 有
G1(s)=KcαG0(s);
(4)
(5)
添加增益后的开环系统G1(s)的伯德图如图3b所示。系统的相位裕度为0°, 系统需要补偿50°的相位裕度, 但增加超前校正装置会使幅值曲线发生变化, 增益的交界频率会往右移, 需要补偿系统的相位滞后增量, 故在原来基础上增加5°。因此需要的最大相位超前量φmax近似等于55°, 有
(6)
幅值的变化为
(7)
其中, 转角频率ω=1/(αT)。
由图4知, 被控系统的响应速度随着剪切频率ωc的增大而变差, 但剪切频率过大会导致系统性能变坏, 在相位裕度固定的情况下, 合适的剪切频率能让系统的控制性能更优。

图4 不同剪切频率设置下相位超前校正器的控制效果Fig.4 Control effect of phase advance corrector under different cut off frequency
综上, 针对单自由度磁悬浮系统所设计的相位超前校正控制器为
(8)
校正后磁悬浮系统的伯德图如图3c所示。相位裕度约为55°, 符合设计要求。由其奈奎斯特图(图5)可知, 包围(-1, 0)点有一次负穿越, 并且系统有一个开环右半复平面极点, 故系统稳定。
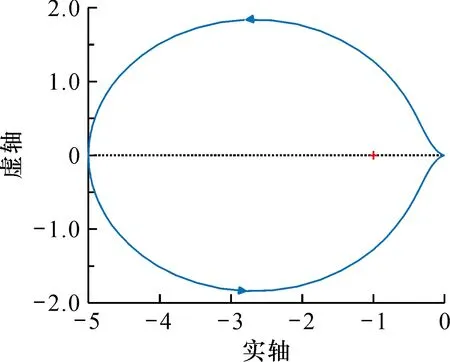
图5 校正后磁悬浮系统的奈奎斯特图Fig.5 Nyquist diagram of corrected magnetic levitation system
3 仿真与实验分析
分别通过相位超前校正控制器与Smith-PID控制器对控制系统进行仿真实验, 如图6所示。其中, PID控制器的具体控制参数为Kp=15、Ki=0.000 1、Kd=32、 采样频率=0.001。
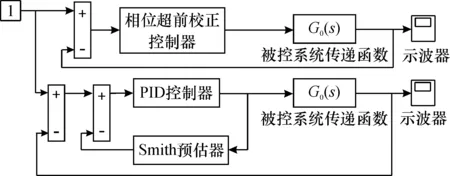
图6 磁悬浮系统相位超前校正与Smith-PID仿真程序对比Fig.6 Comparison of phase advance correction and Smith-PID simulation programs for magnetic levitation system
图7为相位超前校正控制器与Smith-PID控制器阶跃响应曲线对比, 相位超前校正控制的系统相较于Smith-PID控制的系统阶跃响应速度加快, 超调量减小。

图7 相位超前校正控制器与Smith-PID控制仿真阶跃响应曲线对比Fig.7 Comparison of step response curves between phase advance correction controller and Smith-PID control simulation
在Matlab/Simulink中建立单自由度磁悬浮系统的相位超前校正控制器如图8所示, 相位超前校正控制器在单自由度磁悬浮系统实验台完成实时悬浮的实验如图9所示。可知, 钢球的悬浮位置δ基本稳定在7.8×10-3m处, 根据系统的比例关系换算, 与图8最初给定的位移一致, 满足预期目标。
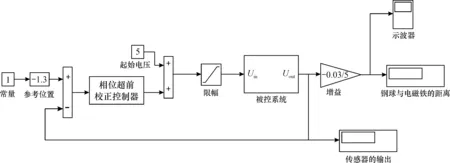
图8 相位超前校正控制器实时控制磁悬浮球程序Fig.8 Program for real-time control of magnetic levitation ball by phase advance correction controller

图9 系统稳定时的磁悬浮球Fig.9 Suspension of magnetic levitation ball in stable system
图10为相位超前校正控制与Smith-PID控制的实时位移比较。相位超前校正控制与Smith-PID控制相比, 位移波动幅度较小, 稳定性得到了提高。
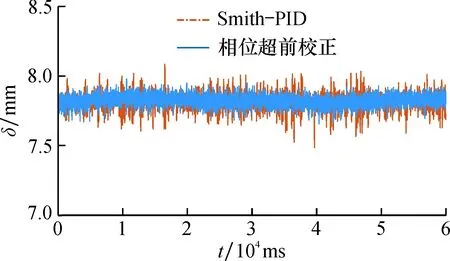
图10 相位超前校正与Smith-PID控制器位移比较Fig.10 Comparison of displacement between phase advance correction controller and Smith-PID controller
4 结 论
针对磁悬浮系统的时滞问题, 提出相位超前校正控制器, 并将其与Smith-PID控制器在磁悬浮系统上进行仿真与实时实验对比, 得到以下结论:
(1)采用相位超前校正控制器后, 减弱了磁悬浮系统相位的滞后, 提高了系统的收敛速度, 缓解了磁悬浮系统的时滞问题。
(2)相比于Smith-PID控制的磁悬浮控制系统, 基于相位超前校正控制的磁悬浮系统的位移波动幅度减小, 稳定性明显提高。
