基于深度学习的气象要素时空预报策略——直接预报和迭代预报的对比

曾安捷 华维 严中伟 祖子清 娄晓 于小淇 夏江江

1 成都信息工程大学，成都 610225

2 中国科学院大气物理研究所东亚区域气候—环境重点实验室，北京 100029

3 中国科学院大学地球与行星科学学院，北京 100049

4 国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室，北京 100081

1 引言

气象要素的时空预报问题是天气气候预报中一个重要的研究课题。近年来，随着可用气象观测数据的增多以及计算机技术的发展，机器学习，特别是深度学习方法被越来越多地应用于天气气候预报问题中。周康辉等（2021）总结了传统机器学习方法和深度学习方法在强对流监测、短时临近预报和短期预报领域的应用，对目前机器学习存在的问题和未来发展方向进行了讨论。贺圣平等（2021）在关于机器学习方法在气候预报中的应用的研究中，介绍了机器学习方法和卷积神经网络（Convolutional Neural Network, CNN）的原理，并利用卷积神经网络对东亚冬季温度进行了建模回报。在北京地区体感温度误差和华北气温多模式集合预报的订正问题中，机器学习方法均取得了较好的效果（门晓磊等, 2019; 武略等, 2022）。Zhou et al.（2022）利用深度学习方法，基于基本数值模式变量进行定量降水预报，预报效果超过了欧洲气象中心的ECMWF HRES高分辨率数值模型。

在气象要素的临近预报问题中，以长短期记忆网络（Long Short-Term Memory, LSTM）结合卷积神经网络CNN为主要结构的卷积长短期记忆模型ConvLSTM （Shi et al., 2015）和预报循环网络PredRNN（Wang et al., 2017）被用来进行雷达回波的时空预报。这类模型主要是基于能直接提取时序信息的循环神经网络（Recurrent Neural Network,RNN）构建的。在基于RNN结构的预报中，韩丰等（2019）利用具有空间记忆模块和时间记忆模块的ST-LSTM（SpatioTemporal LSTM）单元构建模型，对雷达反射率进行预报，其预报效果超过了业务使用的交叉相关法。

近年来，有较多的研究以卷积神经网络CNN为主要网络结构构建时空预报模型。一般来说基于CNN结构的模型能够较好地捕捉空间信息（Reichstein et al., 2019），常用于和图像处理相关的问题中。但基于CNN结构的模型也能利用卷积结构将时间序列图像叠加在通道或深度维度上，隐式地处理时空序列预报问题（Prudden et al., 2020;Hu et al., 2021）。相比基于RNN的预报模型（如ConvLSTM），基于CNN的预报模型的结构更加简单灵活，优化模型所消耗的计算资源更少，被越来越多地应用于时空预报任务（Han et al., 2021;Hu et al.,2021）。

为了预报未来多个时次的气象要素场，基于CNN的模型通常采用不同的预报策略，例如迭代预报策略（Recursive Forecast Strategy, RFS）以及直接预报策略（Direct Forecast Strategy, DFS）（Shi and Yeung, 2018）。RFS模型一般以相对于输入时段气象要素场的下一时次气象要素场为训练目标，通过将上一时次的预报场作为预报下一时次气象要素场的一个输入，迭代使用RFS模型从而实现目标时段的预报（曹伟华等, 2022）。Ayzel et al.（2020）构建了一个基于CNN的雷达回波预报模型RainNet，RainNet输出未来5 min的雷达回波，通过迭代策略RainNet被用于预报未来1 h内12个连续时次的雷达回波。对于较低的降水阈值，RainNet预报效果超过了基于光流法的传统模型，RainNet对较强降水的预报能力有限。

与RFS利用模型自身输出作为新的模型输入进行预报不同，DFS模型直接对目标时段进行训练，不需要借助模型中间输出就能生成目标时段的预报。DFS模型通常有多输出的多时次直接预报模型（Direct Forecast Strategy-Multi steps, DFS-M）和单输出的单时次直接预报模型（Direct Forecast Strategy-Single step, DFS-S）。DFS-M模型在整个目标时段的所有时次上计算损失函数，通过一个模型直接输出多个时次的预报结果。在使用DFS-M预报策略的研究中，Zhang et al.（2019）使用多来源的3维雷达回波数据和气象再分析数据，构建了一个3D卷积模型（3D-cube Successive Convolution Network, 3D-SCN）用于预报对流雷暴的生消发展，该模型的预报效果超过了传统临近预报算法雷暴识别、追踪与外推算法（Thunderstorm Identification,Tracking, and Nowcasting, TITAN ）。Castro et al.（2021）利用时空卷积“序列到序列”网络（Spatiotemporal Convolutional Sequence to Sequence Network, STConvS2S）构建了一个 DFS-M模型，相比于一般的CNN序列预报模型，STConvS2S在训练阶段不会违背输入数据的时间顺序，可以生成超过输入时次长度的预报。其对于气温的预报效果超过基于RNN的基准模型，训练耗时比RNN模型更短。Pan et al.（2021）构建了基于UNet网络变体的混合重分配网络（FUsion and REassignment Networks, FURENet），通过融合额外的偏正雷达数据，FURENet可以更好地预报对流雷暴的演变过程。

DFS-S模型一般由多个子模型构成，每个子模型负责预报目标时段中的一个时次。在使用DFS-S预报策略的研究中，Agrawal et al.（2019）使用UNet模型预报未来1 h的雷达降水，预报效果超过了光流法、持续预报以及一个数值预报模型。Ham et al.（2019）利用CNN直接预报未来某一个时刻的Niño指数，相比动力预报模型CNN模型更善于预报海温的纬向分布。Trebing et al.（2021）提出加入注意力机制的UNet变体模型SmaAt-UNet（Small Attention-UNet），该模型使用更少参数取得了和其他深度学习模型相似的降水预报效果。

通过相关研究可以看出，在使用基于CNN的模型进行临近预报时，可以采用不同的预报策略，但目前缺少针对同一个气象要素临近预报问题使用多个预报策略的研究，此类研究可以通过对比不同预报策略预报效果的差异，分析预报策略对模型预报效果的影响。

本研究以一个气象要素时空预报问题（垂直累积液态水含量）为例，对比基于CNN模型的不同预报策略模型的预报效果，通过深度学习可解释性技术，对导致预报策略间差异的原因进行初步分析，以期为深度学习技术在天气气候预报问题中的应用提供方法参考。

2 数据和方法

2.1 数据

本研究使用风暴事件图像数据集（Storm EVent ImagRy, SEVIR）中的垂直累积液态水含量（Vertically Integrated Liquid water content, VIL）数据作为时空预报问题的数据集。为了有效地训练各种深度学习模型以及验证各个算法在气象应用问题中的效果，美国麻省理工学院林肯实验室Veillette et al.（2020）结合GOSE-16气象卫星以及NEXRAD天气雷达的观测数据构建了风暴事件图像数据集SEVIR，以加速气象问题中深度学习方法的创新。SEVIR数据集是一个时空对齐的图像集合，这些图像记录了2017～2019年在美国大陆上发生的多种天气事件。SEVIR数据集约有20%的天气事件被分类为风暴事件，其余的天气事件被称为随机事件。SEVIR_VIL数据集共包含了18968次天气事件，每一个天气事件的持续时间为4 h，由49个连续的垂直累积液态水含量图像组成，相邻时次的图像间隔5 min，单个垂直累积液态水图像以1 km分辨率覆盖一个384×384的格点区域。SEVIR_VIL中的数据以灰度图的形式进行保存，取值范围是0～255以内的整数。灰度图像的格点值和实际的垂直累积液态水含量（单位：kg/m2）的转化规则如表1所示，灰度值255代表缺测。

表1 灰度图格点值和垂直累积液态水含量之间的转换关系Table 1 Scaling rule of converting vertical integrated liquid from gray scale image

参照使用SEVIR_VIL数据的已有研究（Hu et al., 2021），本研究将1个天气事件分成了3个单独的训练样本序列，每一个训练样本序列包含25个连续时次图像，其中前13个时次作为输入时段，剩下的12个时次是目标预报时段。本研究将2019年6月1日之前的44760个训练样本序列划分为深度学习模型的训练集和验证集，训练集验证集的数据比例为8∶2，2019年6月1日之后的12133个训练样本序列作为测试集。为了方便模型训练优化，将图像格点值除以255，对数据集整体进行了归一化处理。

2.2 方法

2.2.1 构建RFS和DFS预报策略模型的基础网络结构

本研究使用UNet网络结构作为构建RFS和DFS预报策略模型的基础网络结构，由于该网络整体结构像一个大写的英文字母U，故称其为UNet，UNet的具体细节结构可参考文献（Ronneberger et al., 2015）。本研究使用的UNet网络如图1所示，主要结构设计包含：对称的4层编码—解码网络结构，每层编码—解码结构之间都有一个跳跃连接，在解码网络后通过一个1×1的卷积层得到模型的最终输出。编码器由4个下采样模块组成，每一个下采样模块都有2个卷积层和1个平均池化层。每一个下采样模块减小输入图像的大小，同时使其特征图数量翻倍。相对应的解码器由4个上采样模块构成，上采样模块扩展输入图像的大小，同时使其特征图数量减半。每一个上采样模块有1个上采样层和2个卷积层。跳跃连接将编码器中的低层特征同解码器中的高层特征结合在一起，保留了输入垂直液态水含量图像中的多尺度空间信息。

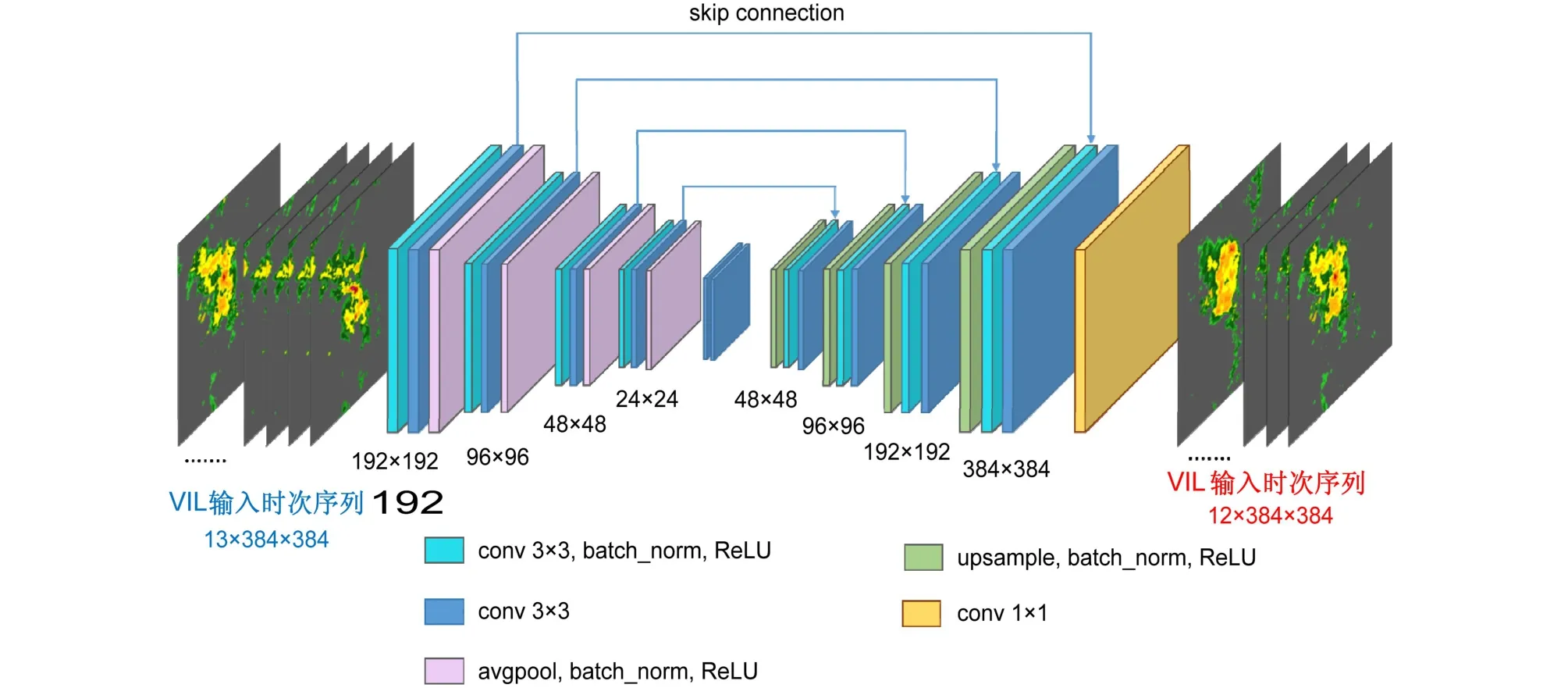
图1 构建三个预报策略模型的基础UNet网络结构Fig. 1 Basic UNet architecture for constructing three forecast-strategy models

本研究的预报目标是构建3种基于基础UNet网络结构的预报策略模型，利用历史13个连续时次的垂直液态水含量图像预报未来12个连续时次的垂直液态水含量图像。因此基础UNet网络的输入图像大小是13×384×384，其中13个通道代表历史13个连续时次。输出图像的大小是12×384×384，其中12个通道代表未来12个连续时次。该网络模型共有899596个可训练参数，训练的迭代轮次设置为50次，训练批次大小为4，在4个NVIDIA GTX 1080Ti显卡上使用pytorch（Paszke et al., 2019）框架进行并行计算，训练耗时约5小时。模型的损失函数为均方误差损失（Mean Squared Error, MSE），使用解耦权重衰减的自适应矩估计优化器AdamW（Loshchilov and Hutter,2019）更新网络参数，学习率为0.0001，权重衰减系数为0.001。

2.2.2 基于基础UNet网络结构的3个预报策略模型

本研究设计了3个基于基础UNet网络结构（2.2.1小节）的预报策略模型，以对比不同预报策略对于深度学习模型预报能力的影响。为尽量保证模型间的预报效果差异只受预报策略的影响，3个预报策略模型均使用同样的网络结构，仅在模型训练时误差计算的时次上有所不同。3个预报策略模型的输入图像大小均为13×384×384，输出图像大小为12×384×384，而在实际预报阶段使用的输出时次取决于模型的预报策略。

第一个预报策略模型是基于迭代预报策略的RFS模型，模型输出相对于输入时段下一时次的垂直液态水含量图像。模型自身输出的预报作为进行下一次预报的一个新的输入时次，同原始输入时次结合，组成模型新的输入时段（图2中间输入序列），以此迭代生成下一时次的垂直液态水含量图像。因此目标的多时次预报是通过迭代使用12次RFS模型实现的，其预报流程如图2所示。为了简便该RFS模型被记为RFS-O（Recursive Forecast Strategy-One step）模型（“O”代表模型输出1个时次的垂直液态水含量）。

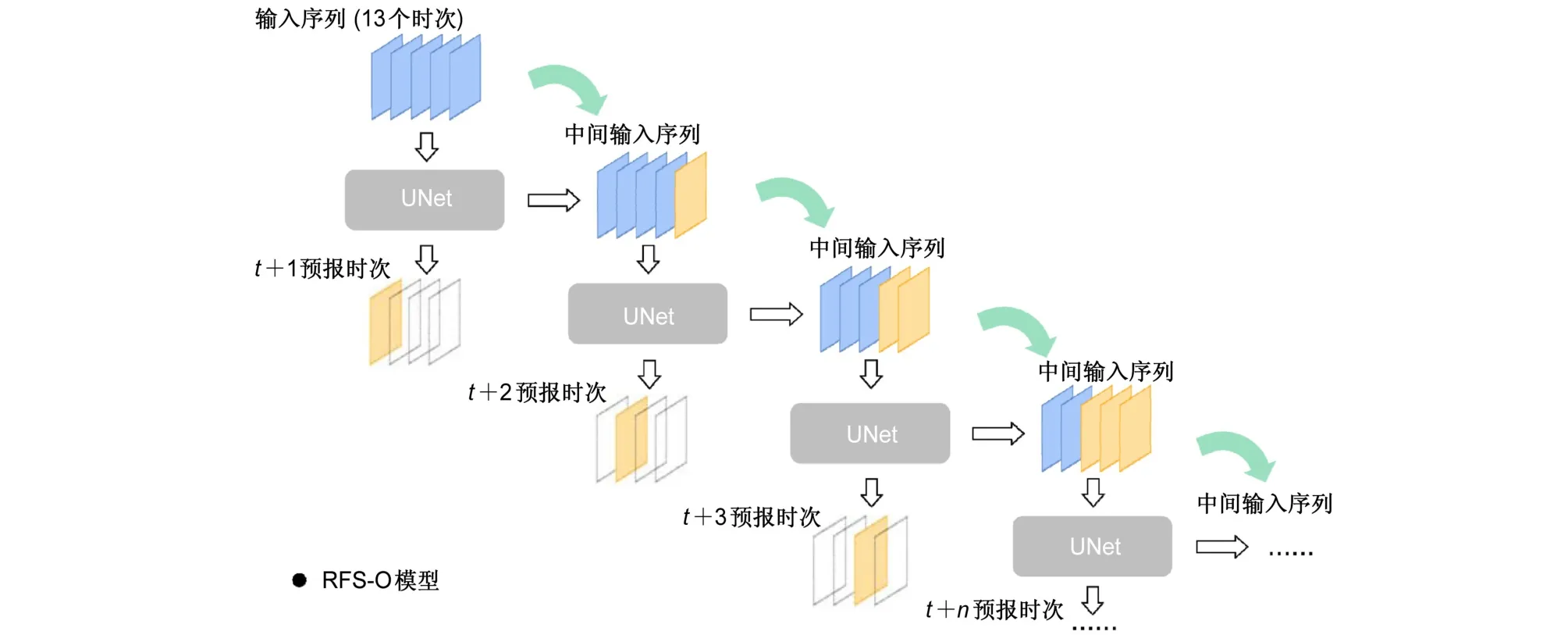
图2 RFS-O模型预报流程示意图Fig. 2 Forecast process of RFS-O model

第二个模型是基于直接预报策略的多时次输出模型DFS-M。DFS-M模型同时预报未来12个时次的垂直液态水含量图像，模型实际采用的预报时次即为模型的全部输出：12×384×384，其预报流程如图3所示。

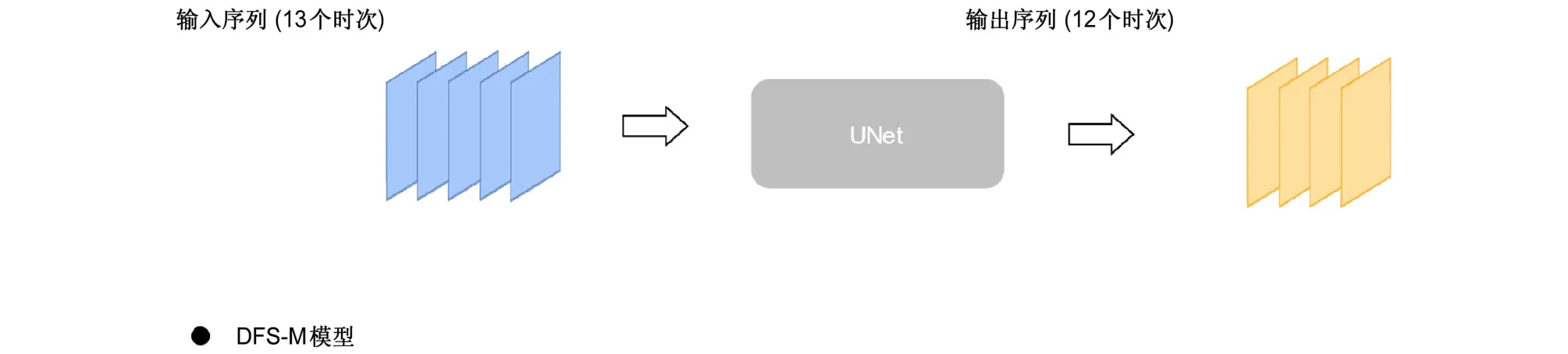
图3 同图2，但为DFS-M模型Fig. 3 Same as Fig. 2, but for DFS-M model

第三个模型是基于直接预报策略的单时次输出模型DFS-S。一个DFS-S子模型只预报单个时次的垂直液态水含量图像，与RFS-O模型迭代使用同一个模型进行预报不同的是，DFS-S模型同时训练12个DFS-S子模型来预报目标时段，每个子模型负责预报特定的1个时次（其预报流程如图4所示）。

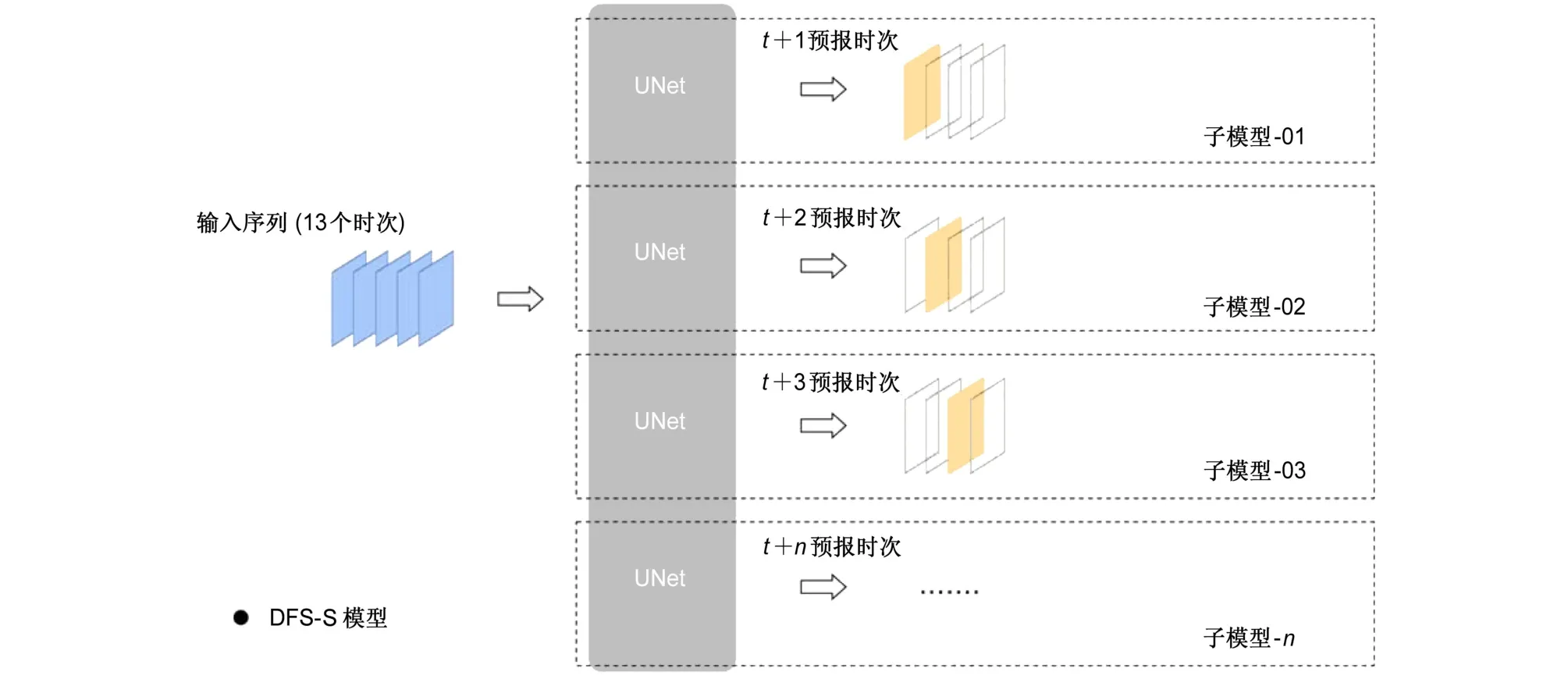
图4 同图2，但为DFS-S模型Fig. 4 Same as Fig. 2, but for DFS-S model

使用一张NVIDIA GTX 1080Ti显卡进行预报测试，经过训练后的3种预报策略模型的单次推断耗时如图5所示。RFS-O模型的预报耗时最高，约为0.317 s。DFS-M模型预报耗时约为0.007 s，预报速度最快。DFS-S模型进行一次预报约耗时0.086 s。

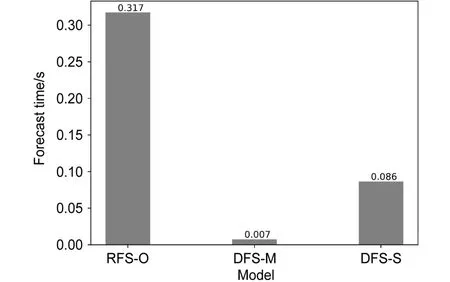
图5 RFS-O、DFS-M和DFS-S模型进行一次预报的耗时Fig. 5 Inference time of RFS-O, DFS-M, and DFS-S models for a single forecast

本研究设计构建了上述3种基于不同预报策略的垂直液态水含量临近预报模型。通过对比每个预报策略模型的预报结果，可以评估不同预报策略的对于模型预报能力的影响。

3 结果

3.1 统计评估指标

本研究利用一些常用的统计评估指标在测试集上评估模型的预报效果，这些评估指标包括均方根误差（Root-Mean-Square Error, RMSE）以及3个基于二维混淆矩阵的降水预报评分（垂直液态水含量与地面降水有直接联系）：命中率（Probability of Detection, POD），临界成功指数（Critical Success Index, CSI）以及虚警率（False Alarm Rate, FAR）。

RMSE代表预报垂直液态水含量图像中格点值同实际观测图像对应格点值之间的平均误差，其计算公式如下：

其中，M和N分别为垂直液态含水量图像的总行数和列数，i和j分别为垂直液态含水量图像中格点所在的行数和列数，公式中的V和Vs分别代表实际观测图像和模型预报图像的格点值。

降水预报评分是在特定阈值下对预报技术有效性的统计评估，通过表2所示的二维混淆矩阵，本研究分别计算POD、CSI和FAR评分，对应计算公式如下：

表2 用于降水预报评分计算的二维混淆矩阵Table 2 Binary contingency table for calculating precipitation forecast verification metrics

其中，TP代表真正例（True Positive）相同格点位置的垂直液态水含量观测值和模型预报值都超过特定阈值的格点数量，FN是假反例（False Negative）观测值超过特定阈值而预报值在该阈值之下的格点数量，FP是假正例（False Positive）观测值低于特定阈值而预报值超过该阈值的格点数量。

本研究所使用的3个降水评分的取值范围均为0～1，其中POD和CSI越接近1，FAR越接近0，代表模型的预报效果越好。

3.2 模型预报效果对比

3.2.1 模型在整体预报时段上的预报效果

本节对比使用不同预报策略的模型：RFS-O、DFS-M和DFS-S，在12个预报时次上的平均预报效果，计算各预报策略模型在测试集上预报结果的平均RMSE误差及以20为阈值的POD、CSI和FAR评分，其结果如表3所示。采用直接预报策略的模型（DFS-M和DFS-S）在4个统计评分中有3个（除了FAR）都优于采用迭代预报策略的RFS-O模型，DFS-M和DFS-S的平均RMSE低于RFS-O约19%，POD和CSI分别高于RFS-O模型27%和12%。DFS-M模型在除了FAR的统计评估指标上都略微优于DFS-S模型。在预报耗时方面DFS-M对测试集中全部天气事件进行预报耗时244 s，DFS-S和RFS-O则分别耗时684 s和1345 s。

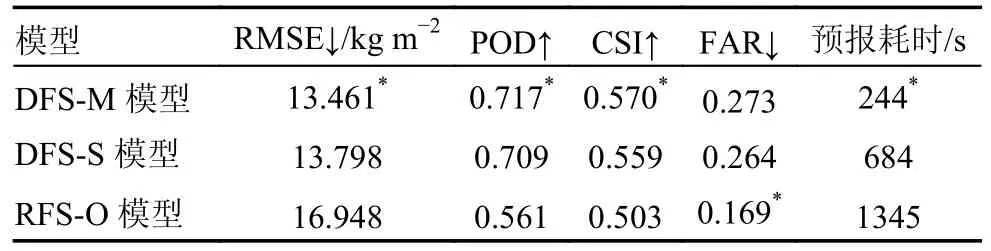
表3 预报策略模型在测试集上的平均统计评分Table 3 Comparison of the averaged statistical forecast scores of RFS-O, DFS-M and DFS-S models on the test dataset

3.2.2 预报策略模型在12个预报时次上的预报效果

图6展示了3个预报策略模型的RMSE、POD、CSI和FAR随预报时次的变化情况。可以看出随着预报时次的增加，预报的不确定性有所上升。3个模型的RMSE、FAR均随预报时次增加而上升，POD和CSI随预报时次增加而下降，模型的综合预报效果随预报时次的增加而下降。

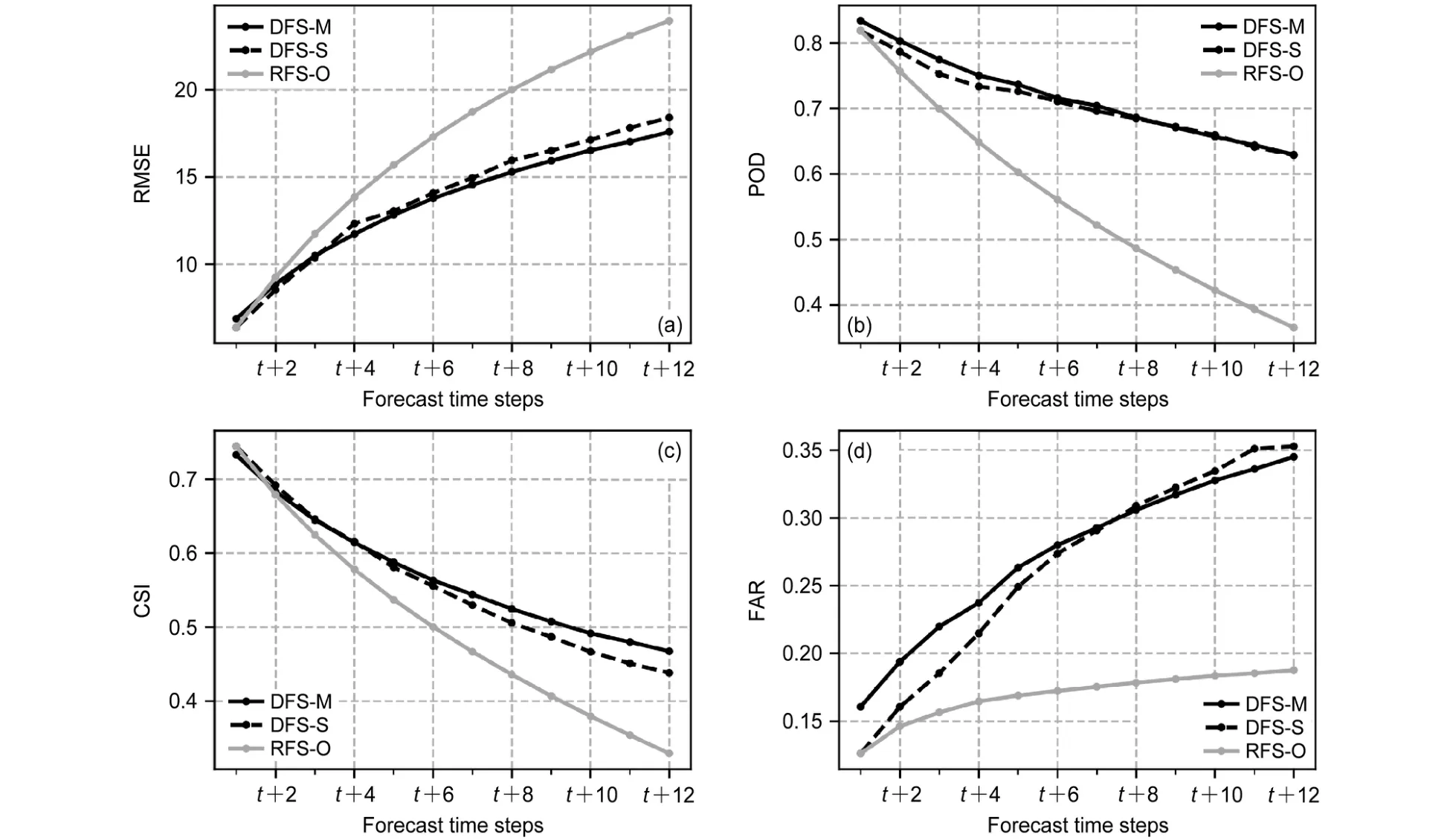
图6 预报策略模型的（a）RMSE（单位：kg m-2）、（b）POD、（c）CSI和（d）FAR随12个预报时次的变化Fig. 6 Variations of (a) RMSE (kg m-2), (b) POD, (c) CSI, and (d) FAR of forecast-strategy models over 12 forecast time steps

如图6a所示，随着预报时次的增加，直接预报策略模型DFS-M和DFS-S的RMSE明显优于迭代预报策略模型RFS-O。对于两个直接预报模型，DFS-M在整体预报时段上优于DFS-S模型，对于前两个预报时次的RMSE，DFS-S的预报效果略微优于DFS-M。

从降水预报评分来看，图6b中RFS-O的POD明显低于两个直接预报模型。DFS-M和DFS-S模型的POD评分接近，在前5个预报时次DFS-M的POD略微优于DFS-S模型。在图6c中两个直接预报策略模型DFS-M和DFS-S的CSI优于RFS-O模型，DFS-M的CSI在整体目标时段上优于DFS-S，前3个时次DFS-S模型的CSI高于DFS-M。在图6d中，RFS-O模型的FAR低于DFS-M和DFS-S，DFS-S的FAR在前6个时次低于DFS-M模型。

3.3 天气事件实例分析

为了对比模型预报和实际观测的垂直液态水含量之间的差异，本研究随机选取模型测试集中的一次降水天气事件，并绘制了该天气事件中，未来6个预报时次的垂直液态水含量分布图，同3个预报策略模型对应时次的输出进行对比分析，如图7所示。每一列代表一个预报时次，第一行是该次天气事件中实际观测的垂直液态水含量分布图，剩下3行为各个模型的对应预报结果。

图7 2019年6月1日（89.6°W～94.9°W，43.3°E～46.6°E）区域测试集一次降水天气事件实例中（d1）观测和（d2-d4）模型预报的t+1时次（第一列）、t+3时次（第二列）、t+5时次（第三列）、t+7时次（第四列）、t+9时次（第五列）和t+11时次（第六列）垂直累积液态水含量分布Fig. 7 Vertically Integrated Liquid water content (VIL) distributions across t + 1 (the first column), t + 3 (the second column), t + 5 (the third column), t + 7(the fourth column), t + 9 (the fifth column), and t + 11 (the sixth column) time steps for (d1) observation and (d2-d4) model outputs within a single weather event from test dataset on 1 Jun 2019 within the region (89.6°W-94.9°W，43.3°E-46.6°E)

如图7所示，3个模型的垂直液态水含量相对实际观测偏低，RFS-O模型的预报结果偏低更明显。DFS-M模型对于更长预报时次的垂直液态水含量的高值区域预报得更准确，整体来说直接预报策略模型DFS-M和DFS-S对于高值垂直液态水含量的位置和大小的预报都优于迭代预报策略模型RFS-O。随着预报时次的增加，模型预报的主要垂直液态水含量分布区域开始发散，使得预报结果出现模糊现象。RFS-O的预报图像发散较小，同时对垂直液态水含量的预报偏小，这对应了3.2.1和3.2.2小节中RFS-O模型较小的FAR。

3.4 输入时次图像的特征重要性

基于直接预报策略的两个模型DFS-M和DFS-S的对垂直液态水含量的预报效果明显优于基于迭代预报策略的RFS-O，本研究尝试对这两个直接预报模型进行进一步分析。为了对比两个模型的潜在差异，使用深度学习可解释性方法深度学习重要性特征法（Deep Learning Important FeaTures, Deep-LIFT）（Shrikumar et al., 2017）对两个模型输入时次的特征重要性进行了计算。DeepLIFT方法利用反向传播神经网络中所有神经元对于输入特征的贡献，在特定的输入上解析一个神经网络的输出预测。在本研究中，输入特征共有13个，即13个历史时次的垂直液态水含量图像。DeepLIFT方法使用神经网络中神经元的激活值和“参考”激活值之间的差异计算贡献分数，先通过正向传播过程计算各层神经元和“参考”激活间的差异，然后通过反向传播算法逐层推导出模型输入的特征贡献度。通过使用参考差异，DeepLIFT在梯度为零的情况下也能允许神经元传递重要信号，同时也解决了梯度变化不连续的问题。模型在使用DeepLIFT方法后可以得到13个贡献度图像（每个贡献度图像的大小和输入图像相同），本研究定义单个输入时次的特征重要性分数等于该时次贡献度图像的格点绝对值的平均。研究对测试集中的1512个风暴事件使用DeepLIFT，并采用相对重要性分数，也即单个输入时次的特征重要性分数在13个输入时次特征重要性分数之和中的占比，作为每个输入时次重要性的表征指标。

如图8所示是DFS-M和DFS-S模型13个输入时次的相对重要性分数在12个预报时次上的变化曲线。两个模型最主要的区别是DFS-M模型的相对重要性分数在预报时次上的变化稳定，震荡较小，曲线相对光滑。DFS-S模型的相对重要性分数在预报时次上有很大震荡，相邻预报时次间的相对重要性不具有明显的变化规律。如图9所示是两个模型的单个输入时次对于整体预报时段的相对重要性分数，这相当于单个输入时次对于12个预报时次的相对重要性分数之和。两个模型的相对重要性分数都集中在最后几个输入时次上，t-1和t输入时次的重要性占总输入重要性的80%，说明t-1和t时次的输入对于整体预报有很大的影响。

图8 随预报时次增加，模型输入时次（a）t-12、（b）t-11、（c）t-10、（d）t-9、（e）t-8、（f）t-7、（g）t-6、（h）t-5、（i）t-4、（j）t-3、（k）t-2、（l）t-1、（m）t 的相对重要性分数折线图Fig. 8 Line charts of relative importance score evolution with increasing forecast times for input time steps (a) t-12, (b) t-11, (c) t-10, (d) t-9,(e) t-8, (f) t-7, (g) t-6, (h) t-5, (i) t-4, (j) t-3, (k) t-2, (l) t-1, and (m) t for DFS-M and DFS-S models

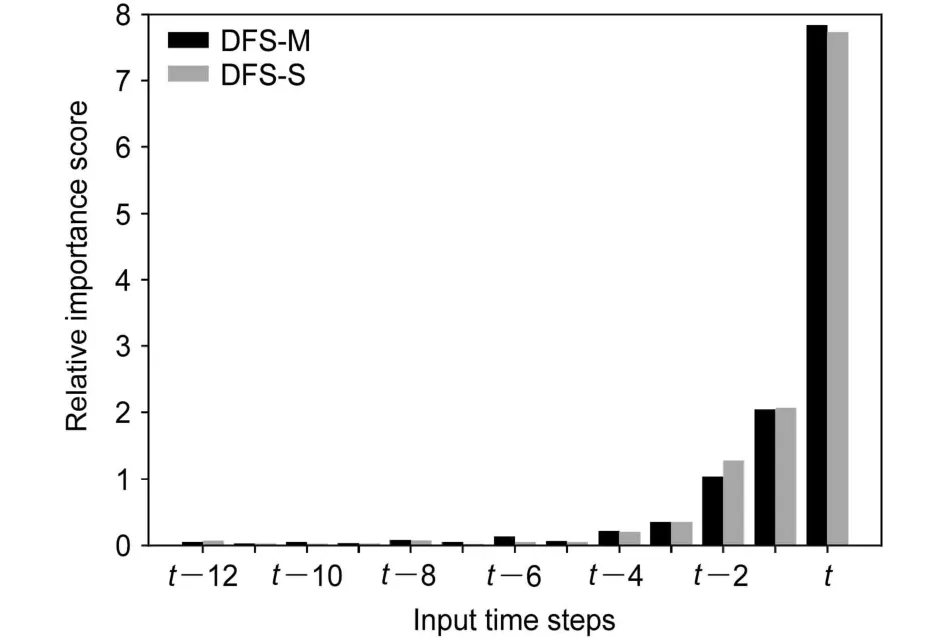
图9 模型13个输入时次在整体预报时段上相对重要性得分的分布Fig. 9 Distribution of 13 input time steps’ relative importance scores on the whole forecast time sequence

DFS-M和DFS-S的输入重要性在12个预报时次上的变化曲线有相似的趋势，研究通过对图8中曲线进行一元线性拟合得到了每个输入时次相对重要性得分变化的斜率，结果如图10所示。前期输入时次（从第t-12到t-2输入时次）的相对重要性随着预报时次增加具有上升趋势，尽管t-1和t输入时次在12个预报时次上的总体重要性占比很高，t-1和t输入时次在单个预报时次上的重要性随预报时次的增加呈现下降的趋势。这说明靠近预报时段的输入时次对于整体预报起主导作用，但其重要性会随着预报时次的增加逐渐下降，前期输入时次（t-12到t-2）对于较长时次的预报的重要性会相对地升高。注意到DFS-S模型的斜率通常大于DFS-M模型的斜率，这说明DFS-M模型的输出时次间存在着一定的约束关系。

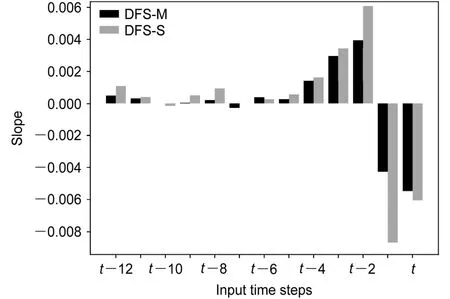
图10 模型13个输入时次相对重要性得分随预报时次变化曲线的一元线性拟合斜率Fig. 10 Slopes of unary linear fit for the variations of 13 input time steps’ relative importance scores over 12 forecast time steps

对于DFS-M的每一个输入时次，重要性在12个预报时次上变化较一致，而DFS-S模型的输入重要性没有明显变化规律，尽管两个模型输入重要性变化趋势相同，DFS-S的变化斜率总是大于DFSM，相对来说DFS-S模型的输入重要性更加不受约束。这些模型特征表明，DFS-M模型能捕捉到12个预报时次间存在的联系，对模型各输出时次的预报结果有一定的约束作用。两个直接预报模型的输入重要性主要集中在最后两个时次，随着预报时次增加t-12到t-2输入时次重要性上升，t-1和t时次重要性下降，这说明在进行较长期预报时，需要重视前几个预报时次对最终预报的贡献。

4 讨论与结论

本研究通过使用经典UNet网络结构构建了3个预报策略模型，基于历史13个时次的垂直液态水含量对未来12个时次的垂直液态水含量图象进行外推预报，对比了一个迭代预报策略模型RFSO和两个直接预报模型DFS-M和DFS-S在气象临近预报中的预报效果。通过对不同模型预报结果的统计评估以及对输入时次重要性的对比分析，本研究总结了这些预报策略模型的优缺点。这里对迭代预报模型和直接预报模型的特征和在不同预报时次的预报效果进行讨论。

和采用直接预报策略的模型相比，RFS-O模型的整体预报效果较差，RFS-O不好的预报表现和模型使用自身中间输出进行迭代预报时误差的累积有关，相似的误差累积也在一些文献中有所提及（Bi et al., 2023）。RFS-O在训练阶段的输入是真实的历史时次垂直液态水含量数据，而在进行实际迭代预报时模型的输入逐步被模型自身输出的预报数据所取代，这种训练和推理阶段的差异使得RFS-O模型比直接预报模型更容易出现误差累积。

对于采用直接预报的DFS-M和DFS-S模型，DFS-M模型在目标时段的平均预报效果优于DFS-S模型。有研究对一般机器学习方法中的时序预报策略进行了对比（Bontempi et al., 2013），该研究表明对于一般的时间序列预报问题，单时次输出的模型是独立训练的，忽略了目标预报时段中每个时次间存在的统计相关性。在本研究中DFS-S模型的每一个子模型都是以单一时次垂直液态水含量图像为标签进行训练的，子模型将其预报的时次看作和余下11个预报时次相互独立。但短时间内大气中含水量的变化是一个连续的过程，因此每一个时次间的垂直液态水含量都存在一定的相关性，但DFS-S模型的训练过程没有考虑这种相关性，影响了DFS-S模型的预报效果。研究通过3.4节中对两个模型的DeepLIFT输入重要性在预报时次上的变化进行分析，进一步说明了这种差异。DFS-S模型对于前几个时次的预报在RMSE、CSI和FAR上略微优于DFS-M模型，可能是由于预报的不确定性会随着预报时次的增加而增加，导致DFS-M模型在训练时的主要误差集中在较为靠后的预报时次，经过反向传播后，模型对靠后的几个预报时次加入了较多预报权重，使得模型对于前几个预报时次的预报效果欠佳（Taieb and Atiya, 2016）。本研究对气象临近预报问题中迭代预报和直接预报策略的讨论，可以类似应用在基于深度学习方法的气候预报问题中。

通过对采用迭代预报和直接预报策略的模型进行对比和分析，研究得出了以下3点主要结论：

（1）迭代预报模型RFS-O的预报误差随着预报时次的增加而快速累积，直接预报模型对目标时段的预报效果优于迭代预报模型。

（2）由于预报时次间的相关性约束，以整个目标时段为标签进行训练的DFS-M模型的预报表现更加稳健，整体预报效果优于以单一时次为标签进行训练的DFS-S模型。

（3）对于直接预报模型DFS-M和DFS-S，模型对于整个预报时段的总体输入重要性主要集中在最后两个输入时次。对于单个预报时次，较早输入时次的重要性随着预报时次的增加而上升。

由于DFS-M和DFS-S对于不同时次的预报效果不同，可以将DFS-S对于前3个时次的预报同DFS-M对后9个时次的预报组合起来，看作一种结合预报的结果。该结合预报在整体目标时段上具有更低的平均RMSE，降水预报评分介于两个模型的降水预报评分之间。