Dilution Crystallization Kinetics of PYX in DMF
2023-10-23LUOXiLIUHongniZHAOJuanCHANGHaiLUANJieyuZHOUWenjing
LUO Xi,LIU Hong-ni,ZHAO Juan,CHANG Hai,LUAN Jie-yu,ZHOU Wen-jing
(Xi′an Modern Chemistry Research Institute, Xi′an 710065, China)
Abstract:For the optimization and scale-up of the dilution crystallization process of 2,6-dipicrylamino-3,5-dinitropyridine(PYX), the dilution crystallization kinetics of PYX was studied in the crystallization system with DMF as the solvent and H2O as the anti-solvent. Firstly, the solubility curves of PYX in DMF pure solvent and DMF-H2O binary solvent were measured by with laser dynamic method, by which the corresponding solubility models were established. And then, the crystal growth type of PYX was determined. The crystal growth and nucleation rates of PYX in the dilution crystallization process were measured, and the corresponding crystallization kinetics models were established. On this basis, the effect factors and laws of the crystallization kinetics of PYX were analyzed. The results show that the solubility of PYX in DMF pure solvent and DMF-H2O binary solvent with different volume ratios increases with increasing temperature, and decreases with increasing H2O content. The solubility of PYX in different solvents was fitted by Apelblat model, where the correlation coefficients of the fitting results are all greater than 0.99. The crystal growth type of PYX is particle size independent growth. The crystal growth and nucleation activation energy of PYX are 8.33×103J/mol and 1.01×104J/mol, respectively. The index of supersaturation ratio to crystal growth rate is 6.73.The stirring strength, supersaturation ratio and suspension density to crystal nucleation rate are 0.27, 7.16 and 0.14, respectively. The crystal growth and nucleation rates of PYX increase along with the increase of temperature and supersaturation ratio. Also, the increase of temperature or supersaturation ratio is more conducive to the crystal nucleation of PYX. Compared with the supersaturation ratio, the stirring intensity and suspension density have less effect on the crystal nucleation rate of PYX, and increasing the stirring intensity or suspension density is detrimental to the crystal growth of PYX.
Keywords:physical chemistry;PYX;DMF; solubility;crystallization kinetics.
Introduction
2,6-Bis(picrylamino)-3,5-dinitropyridine(PYX) was first synthesized by Los Alamos National Laboratory in the United States in the 1970s. PYX is one of the most commonly used heat-resistant explosives, and it is often used in explosive charges requiring extreme heat resistance[1-4]. At present, The crystal morphology of PYX directly synthesized by synthetic process is mostly needle-like or rod-like, and the crystal has large aspect ratio and uneven particle size distribution. Limited by poor crystal formability, PYX has problems such as low bulk density and poor dispersion during application, which makes it difficult to meet the requirements of the charging process of modern weapons[5-8].
Recrystallization is one of the key techniques in the preparation of explosive crystals[9-12]. The crystal formability and performance of PYX can be largely optimized through recrystallization, so that PYX can meet the requirements of charging process. Therefore, recrystallization is of great research significance to the preparation of PYX. Common recrystallization methods include cooling method, dilution method, and melting method, etc. The dilution method is to dissolve the sample in the solvent with good solubility, and then precipitate the crystal by adding the anti-solvent that is almost insoluble to the sample. The dilution method has the characteristics of simple operation, low cost, and high efficiency, and it is a common method of the recrystallization of PYX at present. Riggs[13]used DMSO, DMF as solvent and water as anti-solvent to recrystallize PYX by dilution method. The method improved the shock wave sensitivity of PYX. Wang Baoguo[14]used DMF as solvent and water as anti-solvent to prepare ultrafine PYX crystals with average particle size of 1μm by dilution method. The method reduced the impact sensitivity and improved the energy output of PYX. Li Yongqiang[15]used DMSO, DMF, NMP as solvent and water as anti-solvent to prepare PYX crystals with different morphologies by dilution method. The method decreased the particle size of PYX with DMF or NMP as solvent and increased the specific surface area of PYX. In the previous research, the author found that using DMF as solvent and water as anti-solvent, polygonal block PYX crystals can be obtained by dilution method. The crystal aspect ratio and particle size were obviously decreased, and the uniformity of particle size distribution was greatly improved, which can meet the charge requirements of PYX with small particle size. But there is no relevant research on the dilution crystallization kinetics of PYX, which cannot provide a theoretical basis for the optimization and scale-up of dilution crystallization process. The dilution crystallization kinetics is to study the relationship between crystal nucleation rate, crystal growth rate and driving force in the process of dilution crystallization, and clarify the mechanism of crystal nucleation and growth. The research on dilution crystallization kinetics has very important guiding significance for controlling crystal nucleation and growth.
In this research, the dissolution crystallization kinetics of PYX was studied in the crystallization system with DMF as solvent and H2O as anti-solvent. The solubility curves of PYX in DMF pure solvent and DMF-H2O binary solvent were measured, and the corresponding solubility models were established. Then the crystal growth type of PYX was determined. The crystal growth and nucleation rates of PYX in the crystallization process were measured, and the corresponding crystallization kinetics models were established. On this basis, the effect factors and laws of the crystallization kinetics of PYX were analyzed. The research provides a theoretical basis for the control, optimization and scale-up of the dilution crystallization process of PYX.
1 Experimental
1.1 Instruments and reagents
Crystalline multi-channel crystallizer, Technobis, Netherlands; Master Sizer laser particle size analyzer, Malvern, UK; Constant temperature water bath, Aoxin Electronic Technology Co., China; Glass jacketed reactor, Shubo glass instrument Co., China; Electronic analytical balance, Mettler Toledo, Switzerland.
N,N-dimethylformamide (DMF), analytical reagent, Sinopharm Chemical Reagent Co., China; Deionized water, self-made; PYX, purity≥99.5%, Xi′an Modern Chemistry Research Institute.
1.2 Measurement of solubility
The solubility was measured by laser dynamic method. A certain amount of solvent and excess PYX were accurately weighed and placed in a crystallizer. Then, the temperature was increased according to a certain heating rate under stirring. When the transmitted light intensity reached the maximum value and no longer changed, excess PYX was considered to have completely dissolved. The temperature corresponding to maximum transmitted light intensity was recorded. In this research, the molar fraction was used to express solubility. The solubility calculation formula is as follow:
(1)
In the equation:xis the mole fraction of PYX, mol/mol;mpis the mass of PYX, g.mdis the mass of DMF, g;mwis the mass of water, g;Mpis the molar mass of PYX;Mdis the molar mass of DMF;Mwis the molar mass of water.
1.3 Measurement of crystallization kinetics data
The crystallization kinetics data was measured by intermittent dynamic method. A certain amount of solvent and PYX were accurately weighed and placed in the reactor. The temperature was raised under stirring to prepare the saturated solution, and the saturated solution was held at the set crystallization temperature for 20min. Then, the crystal seed was added to the saturated solution and keep stirring 15min. And then the anti-solvent was added to the saturated solution according to a certain adding rate. The crystal slurry samples were taken at a fixed time interval, and quickly filtered and dried. The sample volume and the mass of dried crystals were recorded, and the particle size distribution of dried crystals was determined. The suspension density(MT) can be calculated by formula (2). The filtrate was evaporated to obtain the solute, and the solute mass was accurately weighed and the solution concentration was calculated. The supersaturation ratio (S) can be calculated by formula (3). The experiment was repeated by changing the crystallization temperature (T), the anti-solvent adding rate (v) and the stirring rate (ω). The experimental scheme of crystallization kinetics is shown in Table 1.
MT=md/V
(2)
S=CS/CB
(3)
In the formula,MTis the suspension density of sample, g/mL;mdis the mass of crystal, g;Vis the volume of sample, mL;Sis the supersaturation ratio;CSis the solution concentration, mol/mol;CBis the equilibrium concentration of solution under the same condition, mol/mol.
2 Results and discussion
2.1 Solubility
2.1.1 Measurement of solubility curve
The solubility of PYX in DMF pure solvent and DMF-H2O binary solvent with different volume ratios was measured at different temperatures. The temperature (T) was taken as the abscissa and the solubility (x) was taken as the ordinate, and the solubility curves are shown in Fig.1.

Fig.1 Solubility curves of PYX in different solvents
Fig.1 shows that the solubility of PYX in DMF pure solvent and DMF-H2O binary solvent increases with the increase of temperature, and decreases with the increase of H2O content. The higher the temperature, the smaller the increase rate of solubility.
2.1.2 Establishment of solubility model
The Apelblat model was used to fit the solubility data, and the fitting results are shown in Table 2. The Apelblat model is as follow:

Table 2 Fitting results of solubility
lnx=A+B/T+ClnT
(4)
In the model,A,B, andCare the model constants;xis the solubility;Tis the temperature, K.
It can be seen from Table 2 that the correlation coefficients (R2) of fitting results in different solvents are all greater than 0.99. It indicates that the fitting results have good correlation, and the solubility of PYX in different solvents can be accurately predicted through Apelblat model.
2.2 Crystal growth type
2.2.1 Measurement of relation curve between particle size and particle number density
The crystal growth rate type can be divided into particle size dependent growth, particle size independent growth, and growth dispersion.The natural logarithm of particle number density has a linear relationship with particle size when the crystal growth rate is independent of particle size, which can be used as the basis for judging the particle size independent growth[16]. In this research, the second sample of experiment No.6 was taken as an example. The particle size distribution of the sample was measured by the particle size analyzer, and the particle size range was decomposed into multiple small particle size ranges. The particle number density of different particle size ranges can be calculated by formula (5). The average particle size of different particle size ranges can be calculated by formula (7).
(5)
(6)
Lia=(Li+Li+1)/2
(7)
ΔLi=Li+1-Li
(8)
In the formula,niis the particle number density of the ith particle size range, number/μm4;φiis the volume percentage of the ith particle size range to the total particle size range;MTis the suspension density, g/mL;kis the crystal morphology factor;ρis the crystal density, g/cm3;Liais the average particle size of the ith particle size range, μm; ΔLiis the width of theithparticle size range, μm.
Liawas taken as the abscissa and lnniwas taken as the ordinate, and the relation curve betweenLiaand lnniis shown in Fig.2.
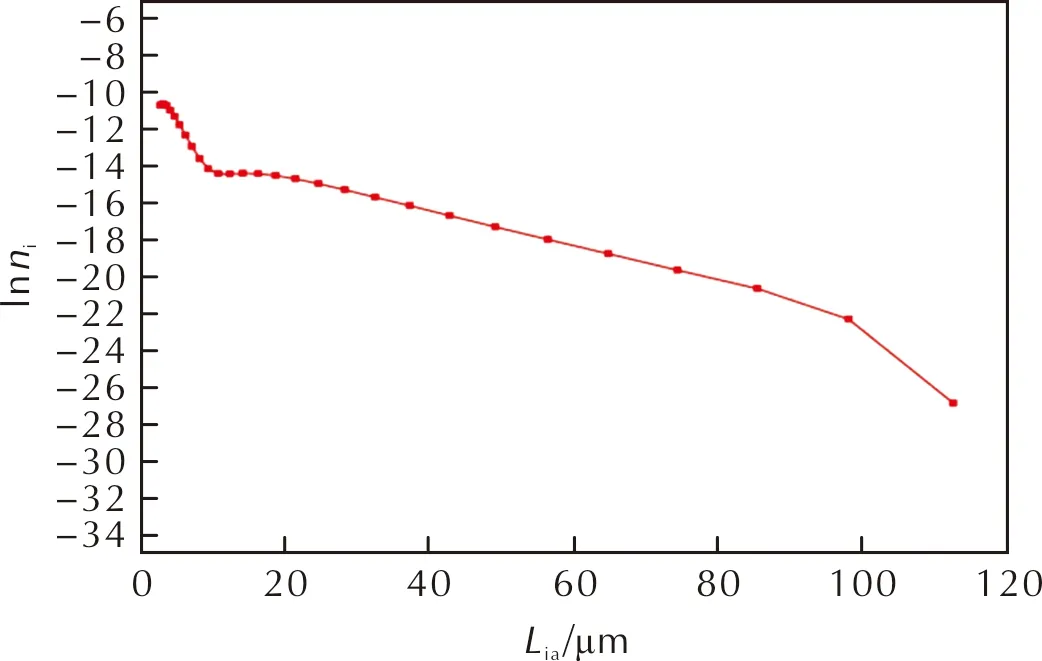
Fig.2 Relation curve between Lia and lnni
Fig.2 shows that the particle size range of PYX is 3.10—112.47μm. For most of the particle size range in the middle section,Liaand lnnishow a linear relationship.
2.2.2 Determination of crystal growth type
According to Fig.2,Liaand lnniwithin the particle size range of 21.43—85.32μm were linearly fitted, and the fitting result is as follow:
lnni=0.0942Lia-12.5982R2=0.9996
(9)
According to the fitting result, the linear correlation coefficient (R2) betweenLiaand lnniis 0.9996, which shows thatLiaand lnnihave a good linear relationship. It indicates that for most of the particle size range, crystal growth rate is independent of particle size. Thus, it is considered that the crystal growth type of PYX in this crystallization system is particle size independent growth. The average crystal growth rate in the range of 21.43μm to 85.32μm can be used as the crystal growth rate of sampling interval.
2.3 Crystal growth kinetics
2.3.1 Measurement of crystal growth rate
In this research, the laser particle size analyzer was used to measure the particle size distribution of PYX crystals at different sampling times. Combined with the particle number balance equation, the effect of crystal aggregation and fragmentation during crystallization is ignored, and the particle number in each particle size range can be calculated by grading method[17]. According to the grading method, the number of crystal particles in each particle size range can be calculated by formula (10), the growth rate of each particle size range can be calculated by formula (11), and the crystal growth rate of each sampling interval can be calculated by formula (12),
Ni=niΔLi
(10)
(11)
(12)
In the formula,Niis the number of crystal particles of theith particle size range, number/μm3;Giis the crystal growth rate of theith particle size range, μm/s;Gis the crystal growth rate of sampling interval, μm/s;ris the ratio of particle size value between upper and lower boundaries of each particle size range.
In this research, the experiment No.6 was taken as an example. The particle size distribution of crystal at different sampling times was measured. Within the particle size range of 21.43—85.32μm, the crystal growth rate of each particle size range at different sampling intervals was calculated, and the results are shown in Table 3.

Table 3 Crystal growth rate of each particle size range at different sampling intervals
According to formula (12), the crystal growth rates of PYX at sampling interval 1, 2, 3, 4 can be calculated to be 0.0960, 0.0325, 0.0125 and 0.0058μm/s. It indicates that the crystal growth rate of PYX gradually decreases during the crystallization process, and the decrease of crystal growth rate in the early stage of crystallization is greater than that in the later stage of crystallization.
2.3.2 Establishment of crystal growth kinetics model
For particle size independent growth, the empirical equation of crystal growth rate is often expressed by formula (13):
(13)
In the formula,Gis the crystal growth rate, μm/s;Sis the supersaturation ratio;kgis the pre-exponential factor;Egis the crystal growth activation energy, J/mol;Tthe temperature, K;Ris the gas constant, 8.314J/(K·mol); g is the constant related to crystallization conditions.
According to the experimental scheme, the crystal growth kinetics data under different crystallization conditions was measured, including crystallization temperature (T), supersaturation ratio (S) and crystal growth rate (G). Some data are shown in Table 4.
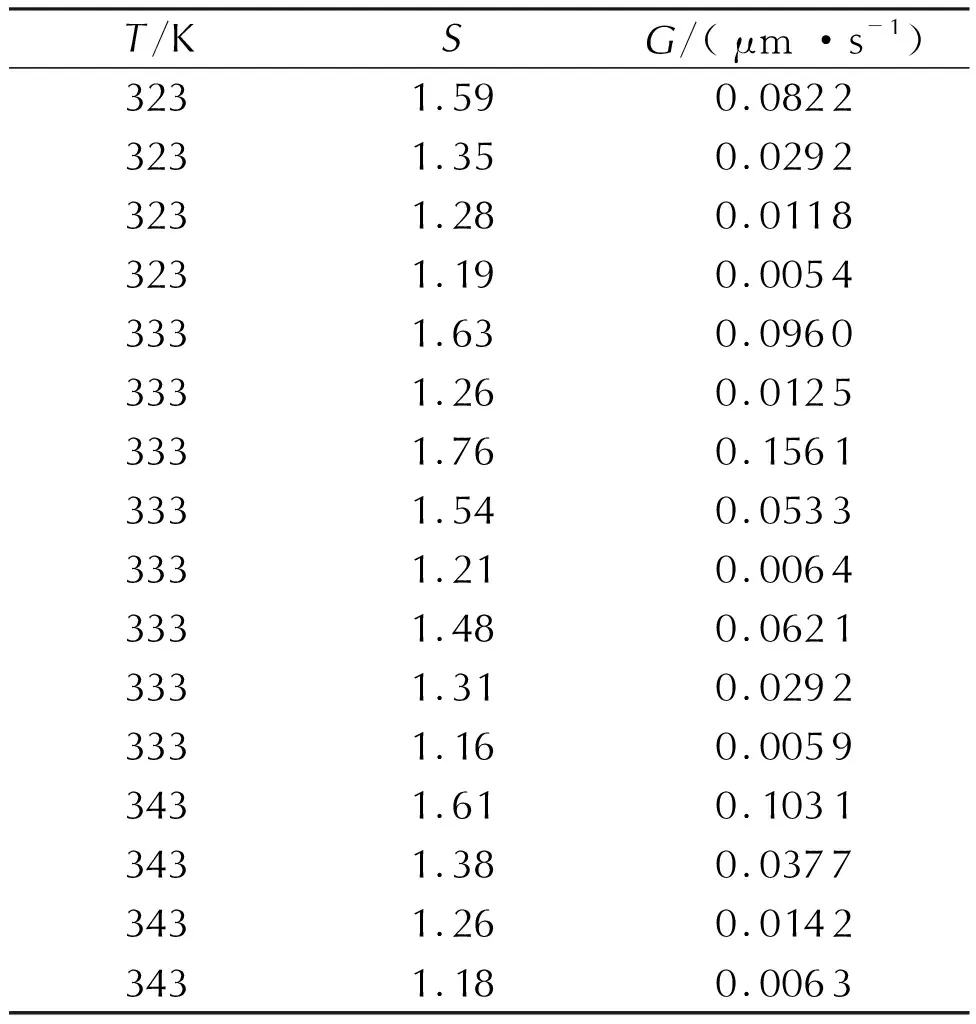
Table 4 Crystal growth kinetics data under different crystallization conditions
According to formula (13), the crystal growth kinetics data under different crystallization conditions was nonlinear fitted, and the crystal growth kinetics model is as follow:
(14)
According to formula(14), the crystal growth activation energy of PYX is 8.33×103J/mol. The higher the temperature, the higher the crystal growth rate of PYX. The index of supersaturation ratio is 6.73, which indicates that the crystal growth rate of PYX increases with the increase of supersaturation ratio.
2.4 Crystal nucleation kinetics
2.4.1 Measurement of crystal nucleation rate
For particle size independent growth, the limit method can be used to calculate the crystal nucleation rate at different sampling intervals by formula (15).
B=Gn0
(15)
In the formula,Gis the crystal growth rate of sampling interval, μm/s;Bis the crystal nucleation rate of sampling interval, number/(μm3·s);n0is the particle number density of the smallest particle size range, number/μm4.
In this research, the experiment No.6 was taken as an example. According to the crystal growth rate of each sampling interval and formula (15), the crystal nucleation rates of PYX at sampling interval 1, 2, 3, 4 can be calculated to be 1.74×10-6, 7.63×10-7, 2.74×10-7and 1.39×10-7number/(μm3·s). It indicates that the crystal nucleation rate of PYX gradually decreases during the crystallization process, and the decrease of crystal nucleation rate in the early stage of crystallization is greater than that in the later stage of crystallization.
2.4.2 Establishment of crystal nucleation kinetics model
Crystal nucleation can be divided into primary nucleation and secondary nucleation. In the crystallization process, primary nucleation is easy to produce explosive nucleation, which makes the crystallization process difficult to control. Therefore, secondary nucleation is the main mode of nucleation in industry. Combined with the diversity and complexity of secondary nucleation, the empirical equation of secondary nucleation is often expressed by formula (16).
(16)
In the formula,Bis the crystal nucleation rate, number/(μm3·s);ωis the stirring intensity, W/m3;Sis the supersaturation ratio;MTis the suspension density, g/mL;knis the pre-exponential factor;Enis the crystal nucleation activation energy, J/mol;Tis the temperature, K;Ris the gas constant, 8.314J/(K·mol);m,n,iare the constants related to crystallization conditions.
According to the experimental scheme, the crystal growth kinetics data under different crystallization conditions was measured, including crystallization temperature (T), supersaturation ratio (S), suspension density (MT), stirring intensity(ω), and crystal nucleation rate (B). Some data are shown in Table 5.

Table 5 Crystal nucleation kinetics data under different crystallization conditions
According to formula (16), the nucleation kinetics data under different crystallization conditions was nonlinear fitted, and the crystal nucleation kinetics model is as follow:
(17)
According toformula(17), the crystal nucleation activation energy of PYX is 1.01×104J/mol. The higher the temperature, the higher the crystal growth rate of PYX. The indices of stirring intensity, supersaturation ratio and suspension density are 0.27, 7.16, 0.14, which indicates that the crystal nucleation rate of PYX increases with the increase of stirring intensity, supersaturation ratio and suspension density. Compared with stirring intensity and suspension density, the index of supersaturation ratio is larger, which indicates that the effect of supersaturation ratio on the crystal nucleation rate of PYX is more significant.
2.5 affecting factors ofcrystallization kinetics
2.5.1 Effect of temperature on crystallization kinetics
Temperature will affect the thermal motion intensity of solute molecules, thus changing the mass and heat transfer efficiency of the crystallization system, and then changing the crystal nucleation and growth rates. According to the crystallization kinetics models of PYX, the effect of temperature on crystal growth and nucleation rates was analyzed. Under the premise ofS,ωandMTunchanged(Sis 1.50,ωis 42.14W/m3,MTis 0.08g/mL), the relation curves betweenG,BandTare shown in Fig.3.
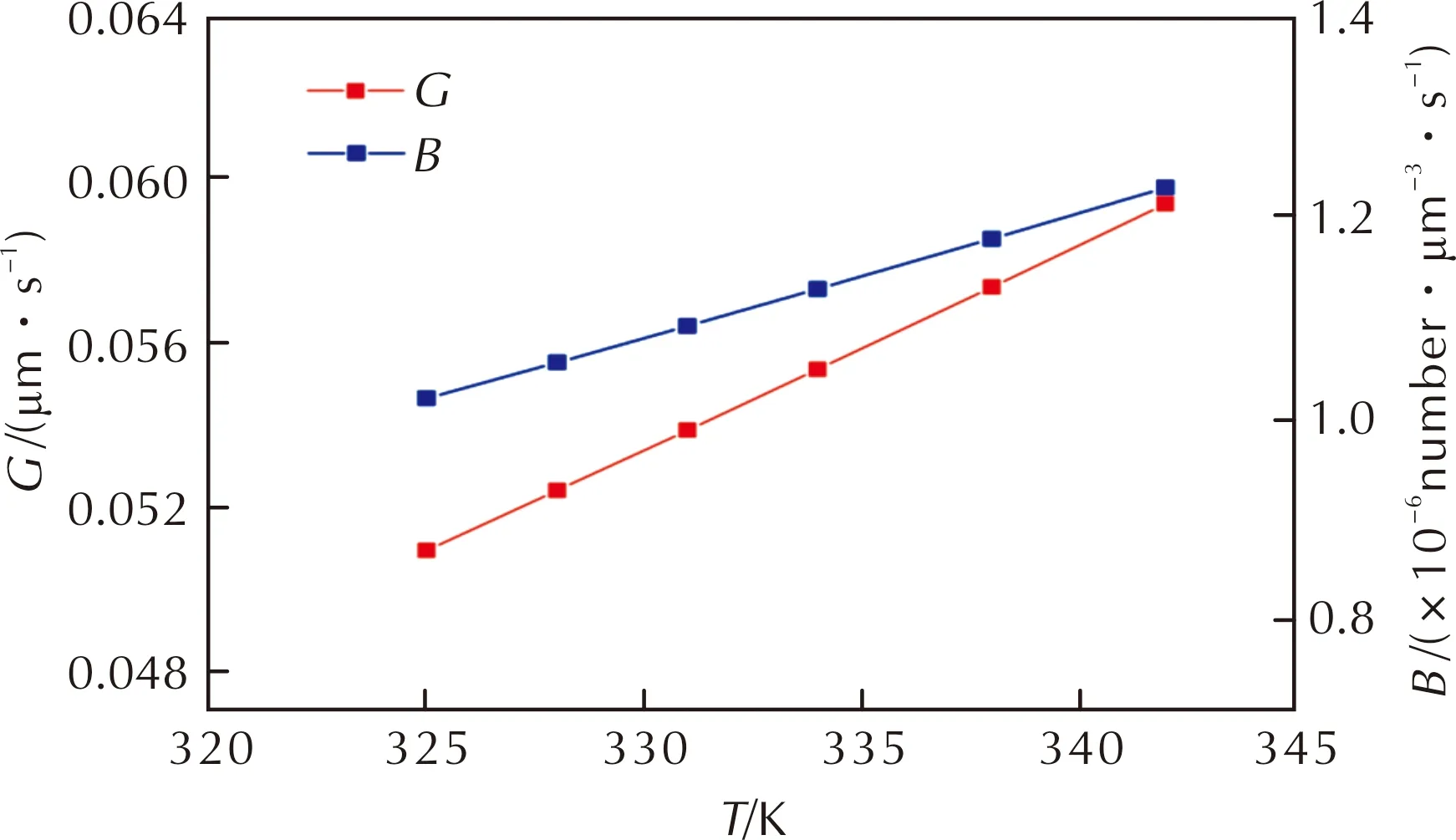
Fig.3 Relation curves between G, B and T
Fig.3 shows that under the certain crystallization conditions, crystal growth and nucleation rates increase with the increase of temperature, which indicates that increasing temperature is conducive to the crystal growth and nucleation of PYX.
In this research,the sensitive characteristics of the change of crystal growth and nucleation rates with temperature were analyzed. Under the premise of other crystallization conditions unchanged,εwas defined as the change rate of crystal growth and nucleation rates caused by increasing unit temperature(1K), and the relation curves betweenTandεare shown in Fig.4.

Fig.4 Relation curves between T and ε
Fig.4 shows that the change rate of crystal growth and nucleation rates gradually decreases with the increase of temperature, which indicates that the change of the crystal growth and nucleation rates of PYX is more sensitive at low temperature range.
In order to analyze the effect weight of temperature on the crystal growth and nucleation rates of PYX, it is assumed thatTis independent ofS,ω, andMT.Twas taken as the variable, and the empirical equations (13) and (16) were taken to be logarithm form and then converted to differential form. The empirical equations obtained are as follow:
(18)
(19)
The equation after subtracting above two empirical equations is as follow:
(20)
Combined with the crystallization kinetic models of PYX,Enis greater thanEg. When the temperature increases, the ratio ofB/Gincreases, and the increase multiple ofBwith the change of temperature is greater than that ofG. Therefore, increasing the temperature is more conducive to the crystal nucleation of PYX, and decreasing the temperature is more conducive to the crystal growth of PYX. Thus, in the process of PYX crystallization, in order to ensure the crystal growth, lower crystallization temperature should be used as much as possible on the premise of meeting the heat demand of crystallization system, so that more solutes can be used for the crystal growth.
2.5.2 Effect of supersaturation ratio on crystallization kinetics
The change of supersaturation ratio will affect the driving force of crystal growth,thus changing the crystal growth and nucleation rates. According to the crystallization kinetics models of PYX, the effect of supersaturation ratio on crystal growth and nucleation rates was analyzed. Under the premise ofT,ωandMTunchanged(Tis 333K,ωis 42.14W/m3,MTis 0.08g/mL), the relation curves betweenG,BandSare shown in Fig.5.

Fig.5 Relation curves between G, B and S
Fig.5 shows that under the certain crystallization conditions, crystal growth and nucleation rates increase with the increase of supersaturation ratio, which indicates that increasing supersaturation ratio is conducive to the crystal growth and nucleation of PYX.
In this research,the sensitive characteristics of the change of crystal growth and nucleation rates with supersaturation ratio were analyzed. Under the premise of other crystallization conditions unchanged,δwas defined as the change rate of crystal growth and nucleation rates caused by increasing unit supersaturation ratio(0.01), and the relation curves betweenSandδare shown in Fig.6.
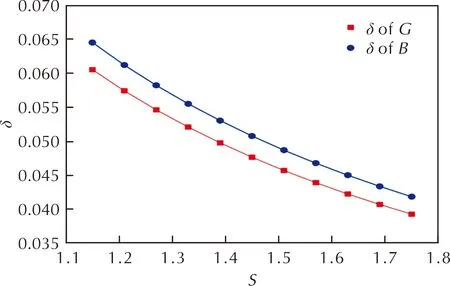
Fig.6 Relation curves between S and δ
Fig.6 shows that the change rate of crystal growth and nucleation rates gradually decreases with the increase of supersaturation ratio, which indicates that the change of the crystal growth and nucleation rates of PYX is more sensitive at low supersaturation ratio range.
Combined with the crystal dynamics model of PYX, The index of supersaturation ratio for the crystal nucleation rate is greater than that of crystal growth rate. Therefore, increasing the supersaturation ratio is more conducive to the crystal nucleation of PYX, and decreasing the supersaturation ratio is more conducive to the crystal growth of PYX. Thus, the supersaturation ratio should be strictly controlled in the process of PYX crystallization and keep it at a low level, so as to prevent the formation of a large number of crystal nuclei and make crystals grow stably.
2.5.3 Effect of stirring intensity and suspension density on crystallization kinetics
The change of stirring intensity and suspension density will affect the distribution of crystal particlesand the flowing state of crystal slurry, thus changing the collision probability between crystals and crystals, crystals and wall, crystals the stirrer, and then changing the secondary nucleation rate. According to the crystallization kinetics models of PYX, the effect of stirring intensity and suspension density on crystal nucleation rate was analyzed. Under the premise ofT,SandMTunchanged(Tis 333K,Sis 1.50,MTis 0.08g/mL), the relation curve betweenBandωis shown in Fig.7(a). Under the premise ofT,Sandωunchanged(Tis 333K,Sis 1.50,ωis 42.14W/m3), the relation curve betweenBandMTis shown in Fig.7(b).
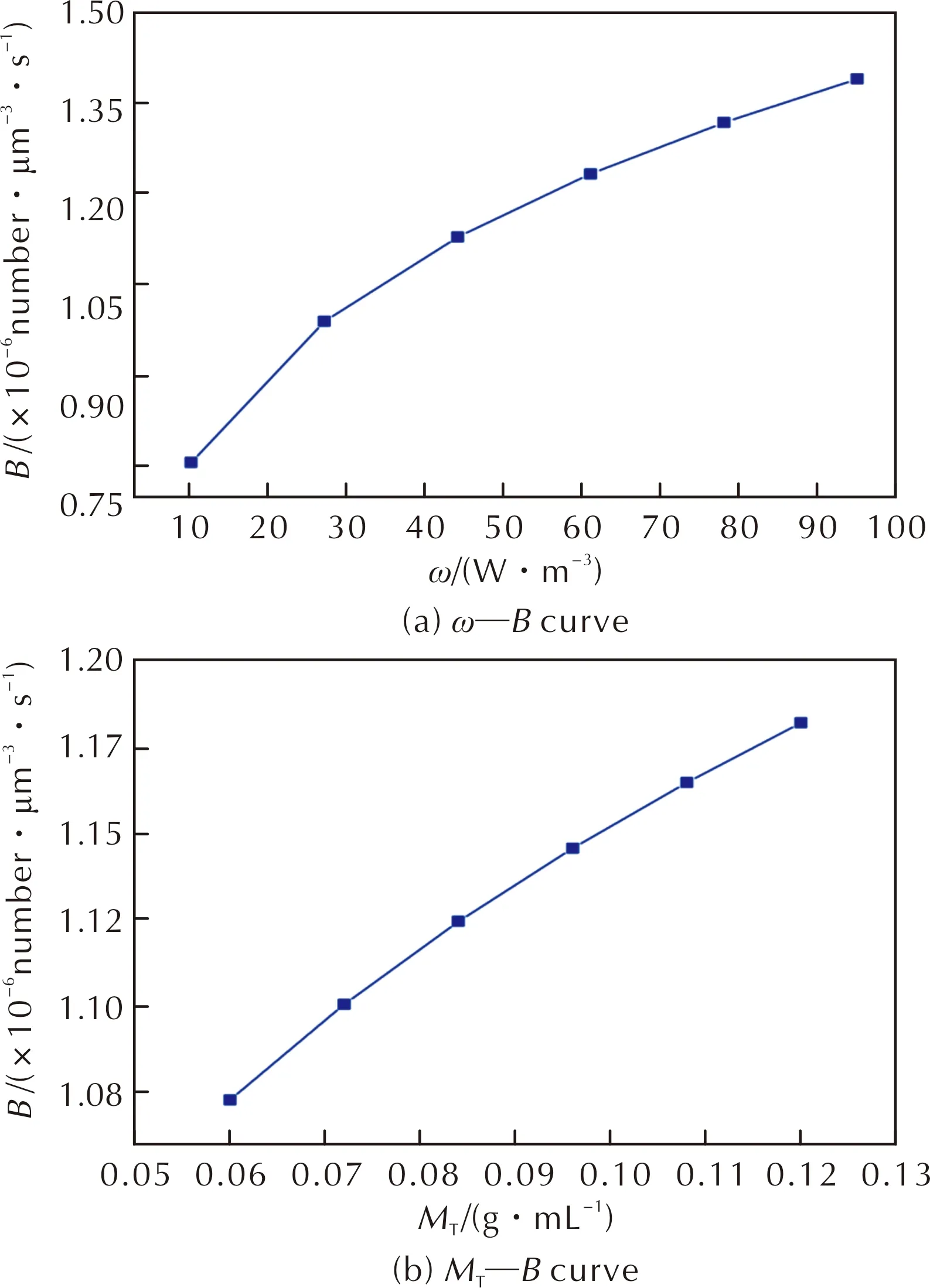
Fig.7 Relation curves between ω, MT and B
Fig.7 shows that under the certain crystallization conditions, crystal nucleation rate increases with the increase of stirring intensity and suspension density, which indicates that increasing stirring intensity or suspension density is conducive to the crystal nucleation of PYX.
Combined with the nucleation kinetics model of PYX, the index of stirring intensity is greater than that of suspension density. So the impact of stirring intensity is more significant than suspension density on the crystal nucleation rate of PYX. On the one hand, this may be because the increase of stirring intensity increases the collision probability of crystal particles, and it will increase the crystal nucleation rate. On the other hand, the increase of stirring intensity increases the shear stress in the fluid boundary layer, which will make some tiny particles that on the crystal surface fall off under the action of shear stress, and further increasing the crystal nucleation rate.
Compared with supersaturation ratio, the indices of stirring intensity and suspension density are smaller. So within the range of experimental conditions, the effect of stirring intensity and suspension density on the crystal nucleation rate of PYX is less than that of supersaturation ratio. However, the increase of stirring intensity and suspension density will increase the crystal nucleation rate but not increase the crystal growth rate, which will be detrimental to the crystal growth of PYX. In addition, there will be more energy input when it is scaled up to industrial crystallization, resulting in more significant effects of stirring intensity and suspension density on crystal nucleation. Therefore, in the crystallization process of PYX, the stirring intensity should be strictly controlled on the premise of ensuring the mass transfer and heat transfer of crystallization system uniform and stable, and the suspension density should be reduced as much as possible on the premise of meeting the demand of crystallization yield to prevent excessive nucleation during the crystallization process.
3 Conclusion
(1) The solubility of PYX in DMF pure solvent and DMF-H2O binary solvent with different volume ratios increases with the increase of temperature and decreases with the increase of H2O content. The correlation coefficients of the fitting results in different solvents are all greater than 0.99, so that the solubility of PYX in different solvents can be accurately predicted through Apelblat model;
(2) In the crystal system with DMF as solvent and H2O as anti-solvent, the crystal growth type of PYX is particle size independent growth, and the crystallization kinetics models of PYX are as follow:
(3)The crystal growth and nucleation activation energy of PYX are 8.33×103J/mol and 1.01×104J/mol. The crystal growth and nucleation rates of PYX increase with the increase of temperature and supersaturation ratio, and the change of crystal growth and nucleation rates is more sensitive at the low range of temperature and supersaturation ratio. The increase of temperature or supersaturation ratio is more conducive to the crystal nucleation of PYX. The crystal nucleation rate of PYX increases with the increase of stirring intensity and suspension density. Compared with the supersaturation ratio, the stirring intensity and suspension density have less effect on the crystal nucleation rate of PYX, and increasing the stirring intensity or suspension density is detrimental to the crystal growth of PYX.
