一种用于SPMSM的改进型滑模模型参考自适应系统观测器*

张 云, 阮承治

(1.南京交通职业技术学院 电子信息工程学院,江苏 南京 211100;2.武夷学院 机电工程学院,福建 南平 354300)

0 引 言

作为国家装备制造业的重要组成部分,电机系统的动稳态性能、运行稳定性及可靠性都影响着机械装备的工作性能。永磁同步电机(PMSM)因其具有无转子损耗、功率密度高、能效高和静态性能好的特性[1-2],而被广泛地应用于运动控制系统中。然而,PMSM矢量系统为了获得高性能的动静态运行品质,需要通过机械式传感器获得准确的速度和位置信息,但PMSM通常工作在恶劣环境中,且机械式传感器容易受环境影响出现故障,从而降低系统的可靠性[3]。

无传感器控制技术的出现解决了上述问题,专家学者们对无传感器控制技术展开了大量研究。目前,无传感器控制技术主要分为两大类:一类为高频信号注入法[4-5],该类方法仅适用于零速和低速;另一类为观测器法,主要为滑模观测器[6-7]、扩展卡尔曼滤波[8-9]和模型参考自适应系统观测器(MRASO)[10]等。其中,由于MRASO结构简单,计算量小而被广泛应用,但其内部的比例积分环节对系统内外部扰动参数敏感,存在鲁棒性不足的问题。为此,文献[11]提出了一种基于模糊PI的MRASO,通过模糊规则实时调整PI的系数,提高系统的动态性能,但模糊算法的引入无疑增加了系统的计算量。文献[12]提出了一种基于饱和函数的滑模变结构模型参考自适应系统观测器,引入滑模控制代替原有的PI控制,提高了系统的鲁棒性,但光滑的饱和函数无法保证系统状态收敛,不利于系统稳定。文献[13]将超螺旋算法(FSTA)和模型参考自适应系统(MRAS)结合,在抑制抖振的前提下,提高了系统鲁棒性。但传统的超螺旋算法无法有效应对线性增长扰动。

为了解决上述问题,本文将FSTA和MRAS相结合,设计出了一种采用带有线性校正项的快速超螺旋滑模模型参考自适应系统观测器(FSTA-SM-MRASO)用于估计电机转速和转子位置。所提观测器将快速超螺旋算法与模型参考自适应系统观测器相结合,构建了基于FSTA-SM-MRASO的SPMSM无传感器矢量控制系统。

1 SPMSM动态数学模型

由于SPMSM的定子电感Ld=Lq=Ls,故而其在旋转坐标系下的动态数学模型为

(1)

式中:id、iq、ud、uq、Ld、Lq分别为d-q坐标系下的定子电流、定子电压及定子电感;ωe、R、φf分别为电角转速、定子电阻和转子永磁体磁链。

对于表贴式永磁同步电机,采用id= 0 的矢量控制方法,其运动方程可以表示为

(2)

式中:Te、TL、p、ωm分别为电磁转矩、负载转矩、极对数和机械角速度。

2 FSTA-SM-MRASO的设计

2.1 MRASO原理

模型参考自适应系统观测器主要由参考模型、可调模型和自适应律组成。其中参考模型不含有待估计参数,可调模型含有待估计参数。当系统工作时,两个模型的输出具有同样的物理意义,然后根据两模型之间的输出误差,设计合理的自适应律对可调模型进行参数更新,使两模型之间的输出误差在系统达到稳态时趋于零。

MRASO基本结构图如图1所示。

图1 MRASO结构图

2.2 传统MRASO的设计

根据MRASO原理,SPMSM动态数学模型分别设置参考模型及可调模型。

首先,令:

(3)

根据式(1)设置参考模型,表示为

(4)

同时,根据式(4)可调模型设置表示为

(5)

式中:带有“^”的变量表示相应的估计值。

将式(4)和(5)相减,可得:

(6)

将式(6)改写为

(7)

(8)

2.3 FSTA-SM-MRASO的设计

由式(8)可知,传统MRASO的转速信息是通过PI控制器来获得的。但在实际工程应用中,PI存在鲁棒性不足的问题,故而采用滑模控制器代替原有的PI控制器。

定义滑模面:

(9)

(10)

由式(10)可知,当系统进入滑动模态时,也就是说参考模型和可调模型的电流相等,即ωeq=ωe。估计转速表达式为

(11)

式中:χ为滑模增益;sign(s)为符号函数。

由式(11)可知,估计转速中含有不连续的开关函数,其在系统中会造成大量的抖振现象,通常需要引入一阶低通滤波器进行滤波处理,但这样无疑增加了系统的复杂性。

为此,本文采用快速超螺旋算法抑制滑模抖振。

常规的超螺旋算法(STA)表示为[14-15]

(12)

式中:u和u1为状态变量;ξ为系统中的未知扰动。

由式(12)可知,常规的STA由于其比例项为开平方计算,这会影响系统的抗突变扰动能力,而且过大的比例项增益会导致系统抖振增大。为此,本文设计一种带有线性校正项的快速超螺旋算法,其表达式为[16]

(13)

式中:ku为线性校正项。

(14)

2.4 系统稳定性证明

为了证明系统稳定性,令:

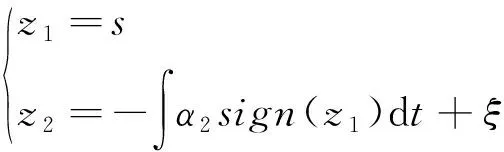
(15)

选取类二次Lyapunov函数为

V(z1,z2)=ζTΠζ

(16)

对式(16)求导得:

(17)

故而:

BTΠζ=(BTΠζ)T=ζTΠT(BT)T=ζTΠB

(18)

令Q=BT∏ζ=ζT∏B,Q2=ζT∏BBT∏ζ可得:

(19)

可以推出:

ζTΠBBTΠζ≥ρζTΠB+ρBTΠζ-ρ2

(20)

(21)

结合式(2),将设计的快速超螺旋滑模模型参考自适应系统观测器应用于表贴式永磁同步电机无传感器控制矢量控制系统,如图2所示。

图2 SPMSM无传感器控制矢量控制系统

3 仿真分析

为了证明所提策略的有效性,本文根据图1,通过MATALAB/Simulink仿真平台搭建基于FSTA-SM-MRASO的SPMSM无传感器控制模型,其电机参数见表1。控制器参数为PI:Kp=15,Ki=3 000;SM-MRASO:ε=400;STA-SM-MRASO:α1=30,α2=40 000;FSTA-SM-MRASO:α1=3,α2=4 0000,k=5 000。

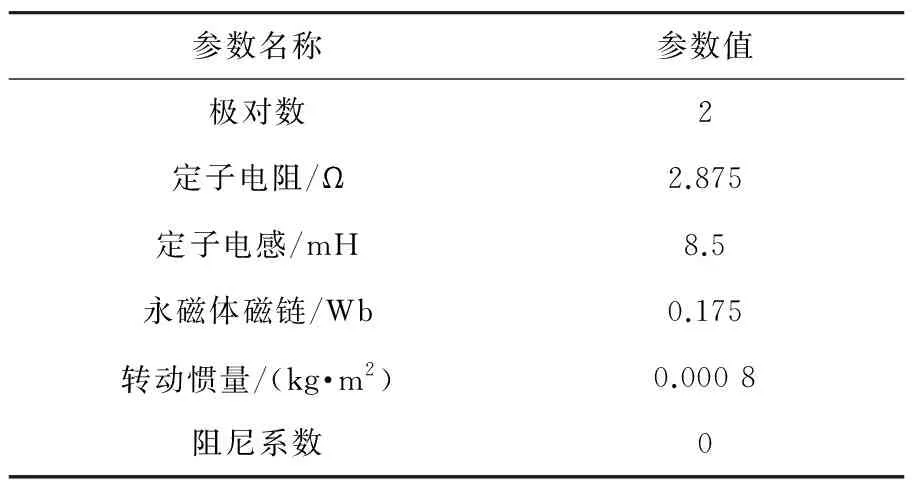
表1 SPMSM参数

图3给出了电机给定转速1 000 r/min空载起动,在0.2 s时,突增负载3 N·m的情况下,SM-MRASO、STA-SM-MRASO、FSTA-SM-MRASO及PI-MRASO四种无传感器控制策略的转速响应及转速误差的仿真图。

图3 转速响应及转速误差仿真图

由图3(a)～(d)转速响应可知,PI-MRASO、SM-MRASO、STA-SM-MRASO及FSTA-SM-MRASO 四种无传感器控制策略都有可行性和有效性,算法的估计转速均能跟踪电机的实际转速。

由图3(e)转速误差可知,在电机起步和0.2 s负载突增阶段,采用PI-MRASO控制策略时,转速估计有较大转速误差波动,算法的估计转速无法准确跟踪实际转速。采用SM-MRASO控制策略时,在电机起步和0.2 s负载突增阶段,转速估计都有着较好的稳定性,但是转速误差是四种方法中最大的。而STA-SM-MRASO和FSTA-SM-MRASO控制策略,虽然在电机起步和0.2 s负载突增阶段都有着良好的稳定性和较小的转速估计误差,但是其中FSTA-SM-MRASO的转速误差最小,动静态性能最好,鲁棒性更强。

图4为电机给定转速1 000 r/min空载起动,在0.2 s时,突增负载3 N·m的情况下,PI-MRASO、SM-MRASO、STA-SM-MRASO及FSTA-SM-MRASO四种不同的无传感器控制策略的电机转子位置响应的仿真图。

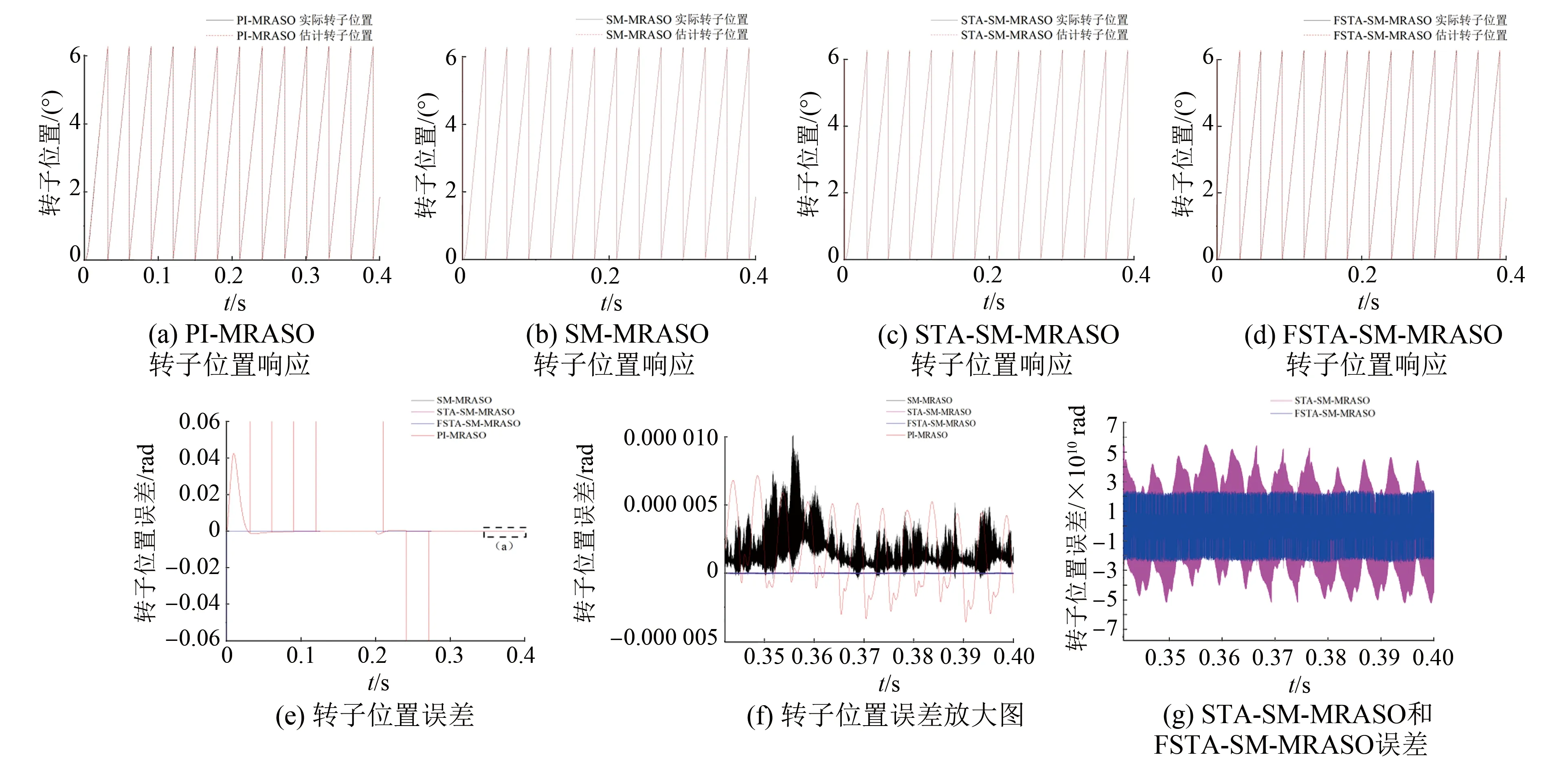
图4 转子位置响应及转子位置误差的仿真图

由图4(a)～(d)转子位置响应曲线可知,SM-MRASO、STA-SM-MRASO、FSTA-SM-MRASO和PI-MRASO四种无传感器控制策略都有可行性和有效性,算法的转子位置均能跟踪电机的转子位置。

根据图4(e)转子误差和图4(f)转子位置误差放大图可知,采用PI-MRASO控制策略时,在电机起步和负载突增阶段,转子位置估计误差最大,并且有较大的误差波动,算法鲁棒性较差。采用SM-MRASO控制策略时,转子位置估计误差比采用PI-MRASO控制策略有所提高,且算法鲁棒性也得到提高。而STA-SM-MRASO和FSTA-SM-MRASO控制策略在电机起步和负载突增阶段,转子位置误差最小,且有着良好的稳定性能。由图4(g)的STA-SM-MRASO和FSTA-SM-MRASO的误差对比图可知,与STA-SM-MRASO相比,引入线性校正项的FSTA-SM-MRASO的转速误差更小,动静态性能更好,能够更有效应对扰动,进一步抑制滑模抖振,提高了系统的鲁棒性。

4 结 语

为了实现高精度、高鲁棒性的SPMSM无传感器控制策略,本文提出了一种基于快速超螺旋滑模模型参考自适应系统观测器。首先,根据电机的动态模型建立模型参考自适应系统观测器;其次,采用带有线性校正项的快速超螺旋算法取代原有的PI控制器,增强了系统整体的鲁棒性;最后,通过仿真对PI-MRASO、SM-MRASO、STA-SM-MRASO及FSTA-SM-MRASO四种无传感器控制策略的转速响应及转速误差进行了对比,证明了所提策略的有效性。