基于模糊- 随机混合空间的机构时变可靠性研究
2023-10-23王佳聪常筠袖
王佳聪, 常筠袖
(辽宁石油化工大学机械工程学院, 辽宁 抚顺 113001)
0 引言
机构作为机械产品的重要组成部分,对机构进行时变可靠性分析很有必要。Andrieu-Renaud 等[1]提出PHI2 方法,将时变问题的求解转变为两相邻相距为时刻Δt,极限状态面从安全范围到失效范围穿越次数问题,利用上穿率计算产品可靠性。Sudret[2]提出新的PHI2 方法,降低两相距时刻Δt 对上穿率计算的影响。Mejri 等[3]在使用随机过程在处理广义强度和应力并考虑时间相关性的基础上,提出新的PHI2 方法。Du[4]以包络函数的思想为基础,通过与一次二阶矩法相结合提出包络函数法求解机构时变可靠性。高明君等[5]提出了一种基于广义强度退化的机构模糊时变可靠性建模方法。孙瑄等[6]建立了模糊时变可靠性建模与分析方法,考虑了随机变量与失效判据的模糊性。
上述学者在计算可靠度指标时主要应用低阶矩法,且求解的准确率有待提高。为进一步增加可靠度的求解精度,文章基于PHI2 方法与四阶矩法,应用4M-PHI2 方法用于求解机构可靠度,针对机构的强度等性能随时间退化情况,建立了机构模糊- 随机混合空间时变可靠性模型,通过对数值算例的模糊时变可靠性分析,验证了方法的准确性。
1 模糊-随机混合空间时变可靠性模型建立
1.1 随机时变可靠性模型
机构所需零件从生产、加工到装配过程中都存在些许误差,这会导致零件的参数具有不确定性,从而造成机构工作过程中的误差。设X=(X1,X2,X3,…,Xn)为机构参数随机变量,t=(0,1,2,…,n)为机构运转时间,φ(ω,t)为随机过程,ω 为变量在所处空间中的位置。机构所产生误差定义为机构实际输出ψ(X(ω),φ(ω,t))和理想输出ψd(t)之差,即:
式中:G[X(ω),φ(ω,t)]为机构时变误差函数。得到机构在运转时间为[t0,tn]范围内的机构时变可靠性概率模型:
式中:ε 为误差阈值。假设误差阈值与机构实际产生误差服从正态分布,根据应力- 强度干涉模型,时变极限状态函数为:
机构时变失效概率为
1.2 模糊- 随机混合空间时变可靠性模型
在时间为[t0,tn]时,考虑误差阈值与机构部分随机变量的模糊性时,机构的时变极限状态函数为:
机构时变失效概率为:
机构的失效概率可表示为:
式中:y 为机构模糊随机混合空间Ω 中的随机变量,定义y 的概率密度函数为fZ(y),μZ(y)为事件状态程度的隶属函数,μZ(y)∈[0,1]。
若μZ(y)为递减函数,将1-μZ(y)考虑为随机变量Y′的概率分布函数,机构的失效域可表述为{X|Z[X(ω),φ(ω,t)]≤Y′},等效极限状态函数为Ze=Z[X(ω),φ(ω,t)]-Y′且仅含随机变量。
同理,若μZ(y)为递增函数,将μZ(y)考虑为随机变量Y″的概率分布函数,机构的失效域可表述为{X|Z[X(ω),φ(ω,t)]≤Y″},等效极限状态函数为Ze=Z[X(ω),φ(ω,t)]-Y″,且仅含随机变量。
进而在给定水平α(0≤α≤1)下,μZ(y)为递增函数时,机构的时变极限状态函数和时变失效概率即可表达为:
2 基于4M-PHI2 方法的模糊-随机混合空间时变可靠度计算
2.1 4M-PHI2 方法
PHI2 方法是以首次穿越法为基础,将计算上穿率问题转变为求解产品t 时刻安全,t+Δt 时刻失效的概率问题[1],如式12 所示。
式中:v+(t)为t 时刻的上穿率;Φ2为二维正态分布的累积分布函数;β(t)和β(t+Δt)为通过一次二阶矩法等方法求解t 时刻与t+Δt 时刻的可靠性指标;ρg为相关系数。
在使用PHI2 方法过程中,单一时刻可靠性指标求解的准确度对后续计算机构的累计失效概率会产生很大影响。与一次二阶矩法等低阶矩法相比,四阶矩法避免了求功能函数偏导数等问题,并且在数值样本偏少的情况下有着高精度的求解结果[8],比较符合处理实际工程中对机构可靠性分析中的现实问题。因此,文章应用4M-PHI2 方法,从而获得更加准确的机构累计失效概率,由此得出:
式中:β4M(t)和β4M(t+Δt)为通过四阶矩法求解的t 时刻与t+Δt 时刻的可靠性指标。
当采用四阶矩法计算t 与t+Δt 两相邻时刻可靠性指标时,相关系数计算方法为:
式中:a(t)与a(t+Δt)为t 与t+Δt 时刻功能函数在验算点处的方向梯度向量,表达式为:
式中:U*为标准正态空间中的验算点,各参数在不同时刻相互关系如图1 所示。

图1 不同时刻参数关系
2.2 模糊- 随机混合空间时变可靠度求解
在α 水平下,设机构的时变极限状态函数为Zαe[X(ω),φ(ω,t)]即时变极限状态面为Zαe[X(ω),φ(ω,t)]=0。在时间[t0,tn]内,机构的失效即可表示为:
在to时刻的瞬时失效概率为:
在时刻t∈[t0,tn],α 水平下的上穿率为:
机构在时间[t0,tn]内的累积失效概率为:
将式(18)带入式(19)中,即可得到累计失效概率求解式为:
3 数值算例
设极限状态的隶属函数为:
引入随机变量Y″得:
即在α 水平下的等效功能函数为:
取α=0.2 时,式中变量分布见表1。

表1 变量分布
从图2 中可以看出,通过使用不同可靠度求解方法对这一典型(累计失效概率直线上升)算例求解后,以MCS(蒙特卡洛)法计算结果为准确值,文章所使用的4M-PHI2 方法相对于经典PHI2 方法与MCS 的曲线贴合程度更高,意味着具有更高精准度,由此证明文章方法的准确性。
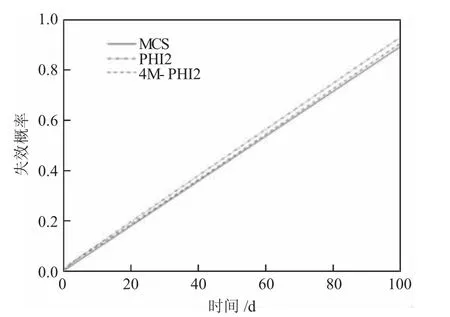
图2 累积失效概率
4 结论
文章基于PHI2 方法与四阶矩法,应用4M-PHI2方法求解机构可靠度,并建立了机构模糊- 随机混合空间时变可靠性模型。
通过算例可以说明,此可靠性模型具有实用性高,误差小的特点。且对于工程中,可根据实际情况确定模糊变量参数α 大小,对于考虑时间累积效应的机构模糊时变可靠性分析具有十分重要的现实意义。
