山西省工业企业创新驱动经济发展的实证分析
2023-10-23郝玺龙杨露豪
郝玺龙, 杨露豪, 张 乐
(1.山西省科技情报与战略研究中心, 山西 太原 030024; 2.稷山县水利局, 运城 稷山 043200)
0 引言
中国经济经历了改革开放后的高速发展阶段,至今已转型高质量发展,GDP 增速也逐渐放缓。这其中促进经济发展的驱动因素也必将迎来转变,在高速发展阶段,主要通过内需、消费、投资、对外出口来拉动GDP,经济结构和布局不合理不科学,发展粗放。当下进入高质量发展阶段后,以前的驱动因素逐渐乏力,那么调整经济结构、优化产业布局显得尤为重要,未来中国经济最大动力是创新驱动,以专利和研发所代表的创新才是长期经济增长的根本动力之一。国内外对创新驱动经济增长的研究已有部分报道。国外经济学家索洛提出“索洛模型”,通过实证分析得出一个国家或地区的经济增长是由技术创新驱动的[1]。在经济学家熊彼特提出创新的概念后,后来的各种实证分析和新古典增长理论都表明创新逐渐成为驱动经济发展的重要因素,尤其是在中国经济新常态下,创新将逐渐成为驱动区域经济持续增长的核心动力[2]。国内开发通过SPSS 实证分析了R&D 经费投入、R&D 人才投入、专利申请量三个创新要素对经济发展的影响,表明三个指标均对经济增长产生了促进的作用[3]。谭志敏等以湖北省为例,实证分析了规上工业企业研发经费与第二产业生产总值增长之间的关系,结果表明前者对后者具有显著的激励效应[4]。
1 数据选取与处理
1.1 数据选取
区域经济增长的关键指标就是国民生产总值(GDP),能反映出区域经济增长速度、经济体量以及国民生活水平等各个方面。关于工业企业创新驱动要素,多数研究认为与R&D 经费投入、专利申请数量有关。R&D 经费投入是企业创新活动的主要投入因素,而有效发明专利数则既是企业创新的主要资源投入,又是创新的主要成果产出,可以市场转化为生产力,这两者的水平直接决定着一个国家或地区的科技创新水平[3-5]。因此选取山西省2011—2021 年的国民生产总值(GDP)与规模以上工业企业有效发明专利数、R&D 经费为统计指标。所选数据皆来源于国家统计局官网中的规模以上工业企业研究与试验发展R&D活动情况和专利情况(2011—2021 年)。
1.2 数据处理
根据山西省2011—2021 年11 年的年度GDP 和居民消费价格指数(上年=100%),将GDP 转换为不变GDP,消除了物价上涨和通货膨胀对实际数据的影响。为了减少不同类型数据之间的差异性,避免因为不同类型数据因量纲差异太大而导致分析结果出现偏差,将数据进行对数化处理。
2 实证分析
2.1 模型构建
如表1 所示,从中发现,不管是山西省GDP 还是规模以上工业企业有效发明专利数,都呈现逐年递增的趋势,规模以上工业企业R&D 经费除2015—2016年有小幅下降以外,其他年份也呈现逐年递增趋势。为了定量分析各个指标之间的关系,以山西省不变GDP 对数(lnGDP)为纵坐标Y,分别以山西省规模以上工业企业有效发明专利数对数(ln 专利数)和规模以上工业企业R&D 经费对数(ln 研发)为横坐标X,利用SPSS21.0 软件作出散点图见图1、图2。
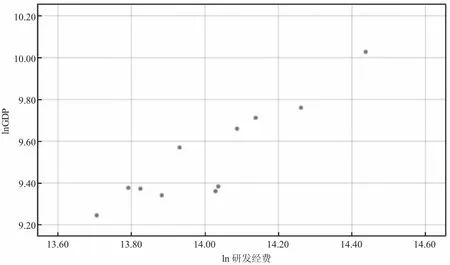
图2 lnGDP 与ln 研发经费的散点图

表1 2011—2021 年山西省规上工业企业有效发明专利数、R&D 经费和GDP
根据国内诸多学者的研究基础[5-8],结合观察散点图,推测lnGDP 分别与ln 专利数、ln 研发经费呈线性回归关系。利用SPSS 进行线性回归分析,并建立了如下方程:
式中:Y 为lnGDP:X 为ln 专利数、ln 研发经费;a 为回归常量;b 为回归系数。经回归分析后,分别得到模型摘要、方差分析表(ANOVA)和系数见表2。
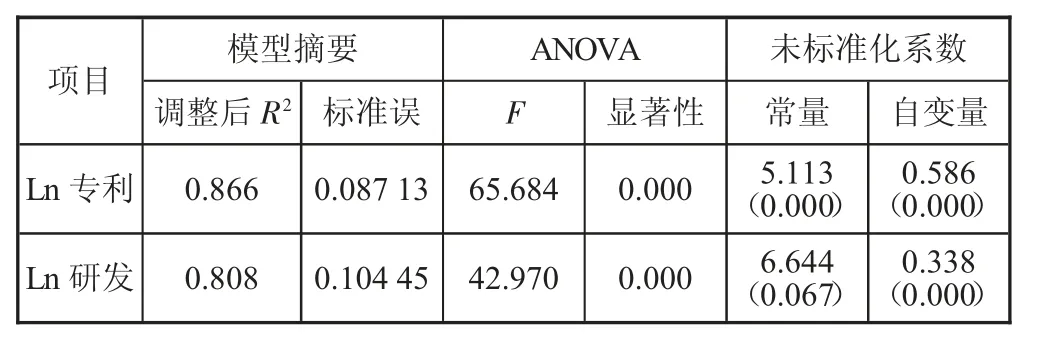
表2 模型摘要、方差分析表(ANOVA)和系数
2.2 模型分析
2.2.1 lnGDP 与ln 专利的回归分析结果
该模型调整后可决系数R2为0.866,表明模型拟合效果较好。它的含义是自变量所能解释的方差在总方差中所占的百分比,该模型中具体指山西省不变GDP 对数的总变差中有86.6%,可以由有效发明专利数对数来解释。ANOVA 方差分析结果中F 统计量等于65.684,概率P 值小于显著性水平0.000,极其显著,所以该模型具有统计学意义,即lnGDP 和ln 专利呈显著的线性关系。表2 还列出了一元回归模型的常量、回归系数的估计值和检验的结果,可知a=5.113,b=0.586,如果以lnG 代表Y,lnP 代表X,其中G=GDP,P=Patent,则公式写为:
经过幂函数变换,公式写为:
GDP 与有效发明专利数之间存在定量幂函数关系,其中常数e5.113>0,幂指数0.586>0,函数在(0,+∞)上单调增加,一定程度上反映出规模以上工业企业有效发明专利数的增长促进了山西省GDP的增长。
2.2.2 lnGDP 与ln 研发经费的回归分析结果
该模型调整后可决系数R2为0.808,表明模型拟合效果较好,在该模型中具体指山西省不变GDP 对数的总变差中有80.8%可以由R&D 经费对数来解释。ANOVA 方差分析结果中F 统计量等于42.970,概率P 值小于显著性水平0.000,极其显著,所以该模型具有统计学意义,即lnGDP 和ln 研发经费呈显著的线性关系。表2 还列出了一元回归模型的常量、回归系数的估计值和检验的结果,可知a=6.644,b=0.338,如果以lnG 代表Y,lnR 代表X,其中G=GDP,R=R&D,则公式写为:
经过幂函数变换,公式写为:
GDP 与R&D 经费之间存在定量幂函数关系,其中常数e6.644>0,幂指数0.338>0,函数在(0,+∞)上单调增加,一定程度上反映出规模以上工业企业R&D 经费的增长促进了山西省GDP 的增长。
在幂函数Y=bXa中,常数b>0,底数X>1 时,幂指数a 越大,函数值Y 也就越大。对于上述模型而言,0.586>0.338,即GDP 与有效发明专利数的幂函数指数大于GDP 与R&D 经费的幂函数指数,因此可以判断有效发明专利数的增长比R&D 经费的增长对GDP 的贡献度更大。
3 结论
根据上述分析,可知山西省GDP 与规模以上工业企业有效发明专利数、R&D 经费均存在定量的幂函数关系,且从回归模型的拟合效果、F 统计量和概率P 值、回归系数的显著性来看,尤其是拟合方程的幂指数,都是有效发明专利数优于R&D 经费,说明为促进经济增长,企业投入的R&D 经费应该重点产出有效发明专利。具体建议如下:
1)加强专利开发和保护意识。对研发和开发专利的企业,通过税收优惠、奖励资助的方式鼓励其加大研发开发力度。以技术专利化、监控市场竞争、建立保密协议、培育专利法务等方式加强保护意识。
2)增加有效发明专利数量。一方面要侧重授权因产品创新和技术革新申请的发明专利,减少授权因工艺创新申请的实用新型专利和因市场创新申请的外观设计专利;另一方面鼓励企业利用社会力量搞研发,建立产学研结合的多元创新意识,利用高校、科研机构的深厚理论功底和基础研究合作开发专利。
3)做强有效发明专利质量。发明专利会因超过法律保护期、未按期缴纳年费、专利诉讼等原因而失效,成为失效专利。对此,企业要在充分调研市场的基础上布局专利战略,采取接力开发、积极成果转化、布局海外同族专利等方式提高维持年限、市场占有率以及专利质量,且优惠政策向战略性新兴产业倾斜,培育高价值专利,响应国家知识产权工作高质量发展的号召。
