一种DEFAULT 密码算法抵抗差分故障攻击新方法

颜林洋 ,郝 婕 ,李灵琛

(1.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004;2.北京市经济管理学校,北京 100142)

1997年,Boneh等[1]针对RSA 密码算法首次提出故障攻击。随后,Biham 等[2]成功将差分故障攻击运用于DES算法的破译。2017年,李浪等[3]通过在DBLOCK密码算法的第17轮多次随机注入故障,平均只需4 次故障就可以恢复其主密钥;2019 年,Khairallah等[4]通过在非线性层注入非均匀分布故障,提出了一种针对SPN 密码结构的差分故障攻击方法,并有效减少了密钥的搜索空间;2020年,Karmakar等[5]针对NIST 候选算法SIV-Rijndael 256提出一种基于经典策略与密钥编排相结合的差分故障攻击方法,且仅使用一个随机字节故障就可以恢复密钥。

另一方面,2010年,李玮[6]通过大量的故障攻击实验,证明了包括DES、AES在内的国际主流密码算法,在不加防护的情况下往往不足以抵抗差分故障攻击。实际上,故障注入攻击的防护技术也不断涌现,主要包括实现级的防护和算法级的防护2种。实现级的防护包括冗余实现、编码校验及感染等实现方式;2015年,张海峰等[7]利用同一输入加密算法的不同级,获取相应的计算结果,验证输出的结果是否一致,判断是否被注入故障,以抵御差分故障攻击;2018年,Patranabis等[8]提出了确定性和随机性2种感染技术来保护AES密码算法,以抵抗差分故障攻击;2019年,Benhadjyoussef等[9]提出了一种基于奇偶校验的错误检测方案,其核心思想是基于奇偶校验对AES 算法进行防护;同年,Lasheras等[10]提出一种通过模糊输出值来应对故障攻击的轻量级防御对策;随后,Aghaie等[11]利用错误检测限制了故障的传播;2020 年,Lasheras等[12]提出一种通过少量冗余检测故障并感染中间状态的轻量级防御对策;同年,Potestad-Ordonez等[13]利用汉明码来检测密码算法中被注入的故障,并将其应用于AES算法,有效保护了AES算法抵御差分故障攻击;随后,Bauer等[14]利用奇偶校验码并发检错基于ARX 的算法;2021年,Rasoolzadeh等[15]同时引入纠错和检错结构,实现对故障攻击的防护。另一方面,算法级的防护方法研究也有一些新进展:2019年,Beierle等[16]提出一种可调分组密码算法CRAFT,并用可调模型来保护其免受差分故障攻击;2021年,Baski等[17]在亚密会上提出了DEFAULT算法,该算法利用具有线性结构的S盒来抵抗差分故障攻击(而无需额外的冗余措施),该密钥长为128 bit的算法版本可以抵抗差分故障攻击,其计算复杂度代价为264次运算;随后,Nageler等[18]分析了DEFAULT算法S盒的线性结构的相关性质,构建等价密钥,用少于100个故障和极低计算代价就可以恢复主密钥。目前DEFAULT 算法仍无法直接抵抗差分故障攻击。如何设计新的防护方案确保DEFAULT 密码算法能有效抵抗故障攻击亟待进一步解决。

基于DEFAULT算法的结构特点,结合冗余实现横向混淆(或纵向隐藏)及线性码提出了一种新的防护方案。该方案使用横向混淆来对冗余部分进行实现,保证算法抵抗非比特级别的故障注入的能力;将具有1 bit纠错能力和4 bit检错能力的[10,4,6]线性码引入防护方案,对每个S盒进行保护。

1 理论知识

1.1 差分故障攻击

1997年,Biham 等[2]提出了差分故障攻击。该方法利用错误密文与正确密文之间的差分,分析密钥信息,其具有攻击点多变、分析复杂度低等特点。该攻击的核心思想是攻击算法的最后几轮,其分析对象是密码的非线性部件S盒:首先构建S盒的扩展差分分布表,其中分布表的输入为〈差分输入,差分输出〉对,输出为S盒可能输入;其次,利用算法结构,每次的故障注入都可以确定相应的〈差分输入,差分输出〉对,查询构建出来的扩展差分分布表,并缩小S盒输入值的可能范围。利用差分故障传播可以捕获轮子密钥,并有效降低主密钥的搜索复杂度。

1.2 差分故障攻击的防护方法

根据防护结果的不同,可以分为基于检测的防护方案和基于感染的防护方案,其中基于检测的防护方案在时间或空间上对算法实现进行复制,并在每个算法部件运行中比较两次实现的结果是否一致,若不一致,判断为故障注入,并结束算法的运行,输出空密文。而基于感染的防护方案会在算法实现时引入一个检测模块,该模块会存储在算法部件实现前后中间状态值,并计算2次保存中间状态值的差分值。对于0输入,感染函数会输出0,对于非0输入,感染函数会输出一个非0的随机值。

算法级的防护方案在近几年也备受关注。这类算法通常不需要额外的冗余实现即可实现对故障注入的防护,比如DEFAULT算法的设计。

1.3 线性码

线性码常被用来错误检测和错误纠错,并被用于故障攻击的检测。以下介绍线性码的相关概念[15]。

定义1一个长为n的码c∈,其中:k是有效信息,n-k为冗余信息,将这个码c称为[n,k]线性码C。

定义2对于一个[n,k]线性码C,一个k×n的矩阵G可以让长为k的原始信息x通过转换C(x)=x·G,转换成一个长为n的对应码字,将矩阵G称为该线性码的生成矩阵。

校验矩阵用于检测一个的元素是否为可能的码字。当收到一个长度为n的码字x∈,判断该码是否为有效码,通常需要使用校验矩阵进行检验。若存在一个n×(n-k)的矩阵H,对于任何c∈(其中0(n-k)表示一个n-k的零向量),则称H为线性码的校验矩阵。

定义3最小距离[n,k]线性码C的最小距离,其中hw(x)表示x的汉明重量。将一个最小距离为d的[n,k]线性码C表示为[n,k,d]码。

引理1[15]对于一个[n,k]线性码C,d=。

引理2[15]对于一个[n,k,d]线性码C,其可以纠正错误码c'=c⊕ec,同时检测错误码c'=c⊕ed,其中e需要满足hw(ed)+hw(ec)＜d,且hw(ed)＜d/2。

1.4 DEFAULT算法

2021年,Baski等[17]提出DEFAULT 分组密码算法。该算法专为抵抗差分故障攻击而设计,其算法整体结构采用SPN 类型,分组长度和密钥长度均为128 bit,轮数为80轮,具体如图1所示,包括DEFAULT-LAYER 层、DEFAULT-CORE 层 及DEFAULT-LAYER层。其中LAYER 层用来抵抗差分故障攻击,而CORE层用来抵抗传统的数学分析。

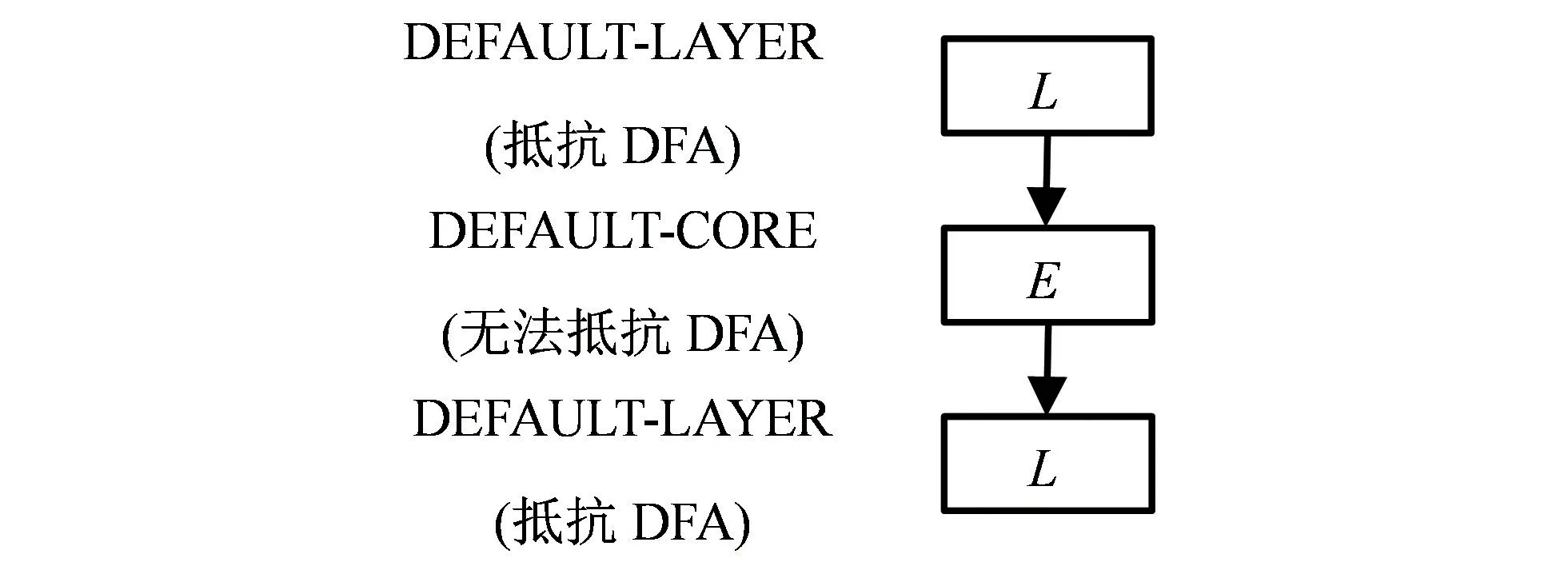
图1 DEFAULT算法结构

算法轮函数结构如图2所示(https://www.iacr.org/authors/tikz/),包括S盒层、比特变换层、轮常量及轮子密钥加4个模块,具体如下。

图2 DEFAULT两轮轮函数结构

1)S盒层。LAYER 层与CORE层的不同在于S 盒选取的不同:LAYER 选取的S 盒是037ED4A9CF18B265(具有线性结构,且能有效抵抗差分故 障攻击)。CORE 选取的 S 盒是196F7C82AED043B5(能抵抗传统数学分析)。

2)比特变换层。如图2所示,上一轮的4个S盒会影响对应下一轮特定的4个S盒,且一个S盒内的比特位映射后的相对位置是不变的,即若第i个比特位映射到第j个比特位,则i≡jmod 4。

3)轮常量加。每轮会有一个6 bit的常量被分别异或在第23、19、15、11、7和3比特位置,而第127比特总是保持翻转。

4)轮密钥加。轮子密钥异或到分组中间状态。

具体的密钥编排方案及解密过程可参见文献[17]。

2 横向混淆和纵向隐藏

根据故障攻击原理可知,实现故障攻击的前提是中间状态发生改变。以往基于检测思想的防护方案,通常使用一个复制冗余实现(复制原来相同的算法实现)来检测另一实现是否被注入故障。但由于原始实现和冗余实现的状态相同,双重故障仍可能成功(如图3所示)。

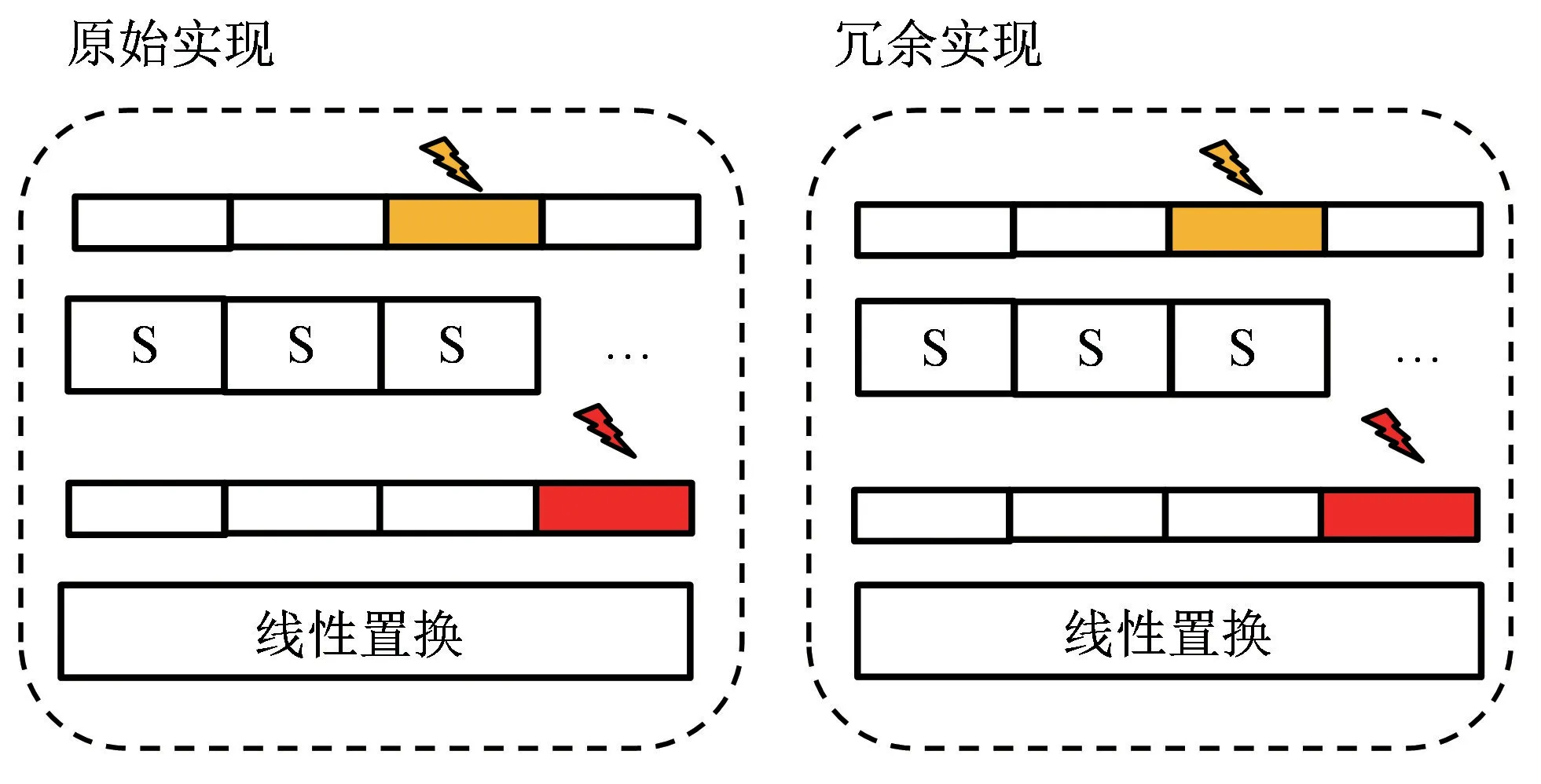
图3 复制冗余的故障攻击方法

为了有效抵抗非比特级故障攻击,在引入冗余的基础上,让冗余与原始实现的中间状态产生差异。这种差异的产生可以通过打乱中间状态或隐藏中间状态来实现,即横向混淆和纵向隐藏。

横向混淆的方法如图4(a)所示,在冗余实现横向打乱中间状态,图中中间状态内的数字表示其对应在中间状态中的序号。根据新的序列状态实现新的S盒和线性变换,可以在保证算法正确实现的情况下只改变中间状态的排序。如果攻击者利用非比特级别的攻击,其无法攻击到与原始实现相对应的比特,比如攻击者攻击了中间状态第4至7个比特,以双重攻击的方法,其会将故障注入中间状态第4、9、6、1个比特位,这样在经过轮函数后,输出的结果并不相同,检测到故障的注入。类似于Adomnicai等[19]提出的GIFT切片实现,是一个典型的横向混淆方法。

图4 基于横向混淆和纵向隐藏的冗余实现

纵向隐藏的方法如图4(b)所示,将算法实现的非线性部件与线性部件结合,形成一个T 实现,如AES的T-BOX实现和白盒实现可以被用来当做一个非常典型的T实现[20,21];该方法隐藏算法运行的中间状态,可以让攻击者无法找到原始实现与冗余实现对应的中间状态。

3 DEFAULT算法的防护方案

DEFAULT的防护方案分为两步:第一步利用横向混淆对DEFAULT 进行冗余实现;第二步利用线性码对每个S盒进行故障的纠错和检错。

3.1 DEFAULT基于横向混淆的实现

整体实现结构如图5所示,轮函数在进入LAYER层后,进行2次运算,分别是原始实现和横向混淆实现,其中进入横向混淆实现前,需先进行初始化。原始实现不改变中间状态的算法实现。横向混淆实现可以借鉴Alexandre等[19]提出的针对GIFT的比特切片方法。横向混淆实现将算法的每个部件单独实现,包括S盒层、比特置换层、轮密钥加和轮常量加4个部件。

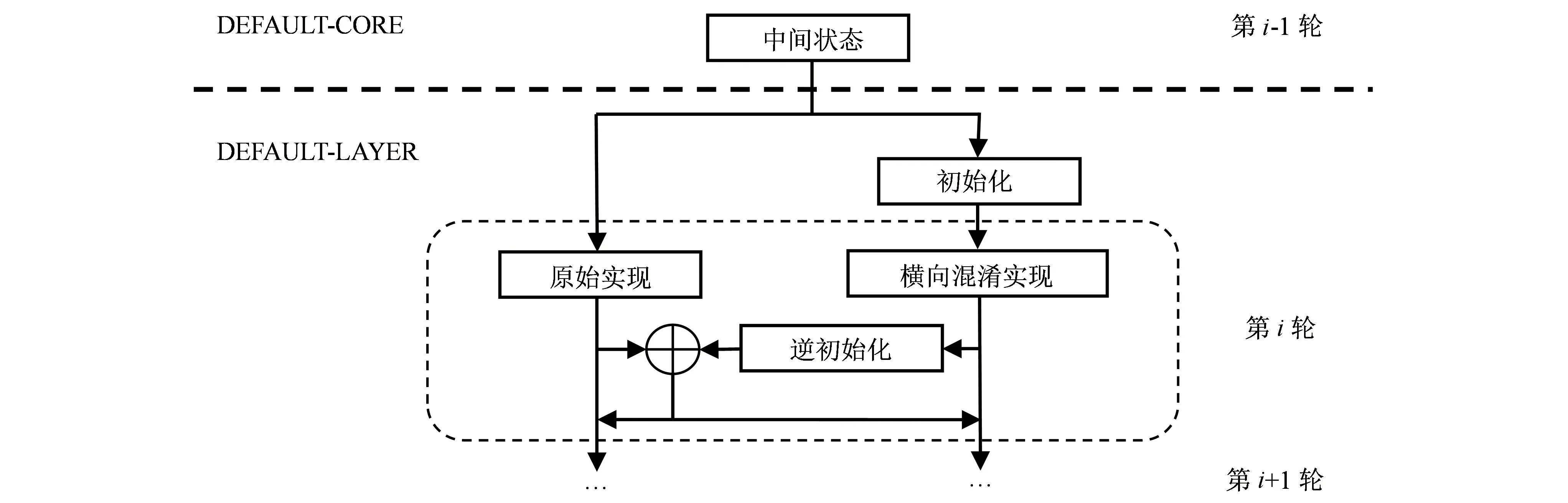
图5 DEFAULT基于横向混淆的实现

在轮函数结束(即完成原始实现和横向混淆实现)时,将横向混淆实现的中间状态逆初始化,比较原始实现的结果和解包后的结果是否一致,若一致,则认为无故障注入,继续进行接下来的轮函数,否则表示有故障注入。

初始化及横向混淆的具体实现如下:

1) 初始化。

如式(1)所示,将明文与轮密钥的所有比特位按4个S盒为一组将比特位的状态按列分别存入4个分组S4i、S4i+1、S4i+2和S4i+3中,0≤i＜8,Sj表示第j个半字节分片,bj表示第j个比特位。

2) S盒层实现。

防护方案只针对算法运行中的第2 个DEFAULT-LAYER进行冗余实现,所以对于横向混淆也只有DEFAULT-LAYER层的S盒。DEFAULTLAYER的4 bit S盒可用式(2)来表达。

其中:Si、S'i分别表示S盒输入和输出的第i比特;⊕表示XOR;·表示AND。

3) 比特置换层实现。

根据原来DEFAULT算法的比特置换和方案分片后的对应比特位置,逐一遍历各比特位,找出新的中间状态对应的比特置换位置,得到具体的置换,如表1所示。

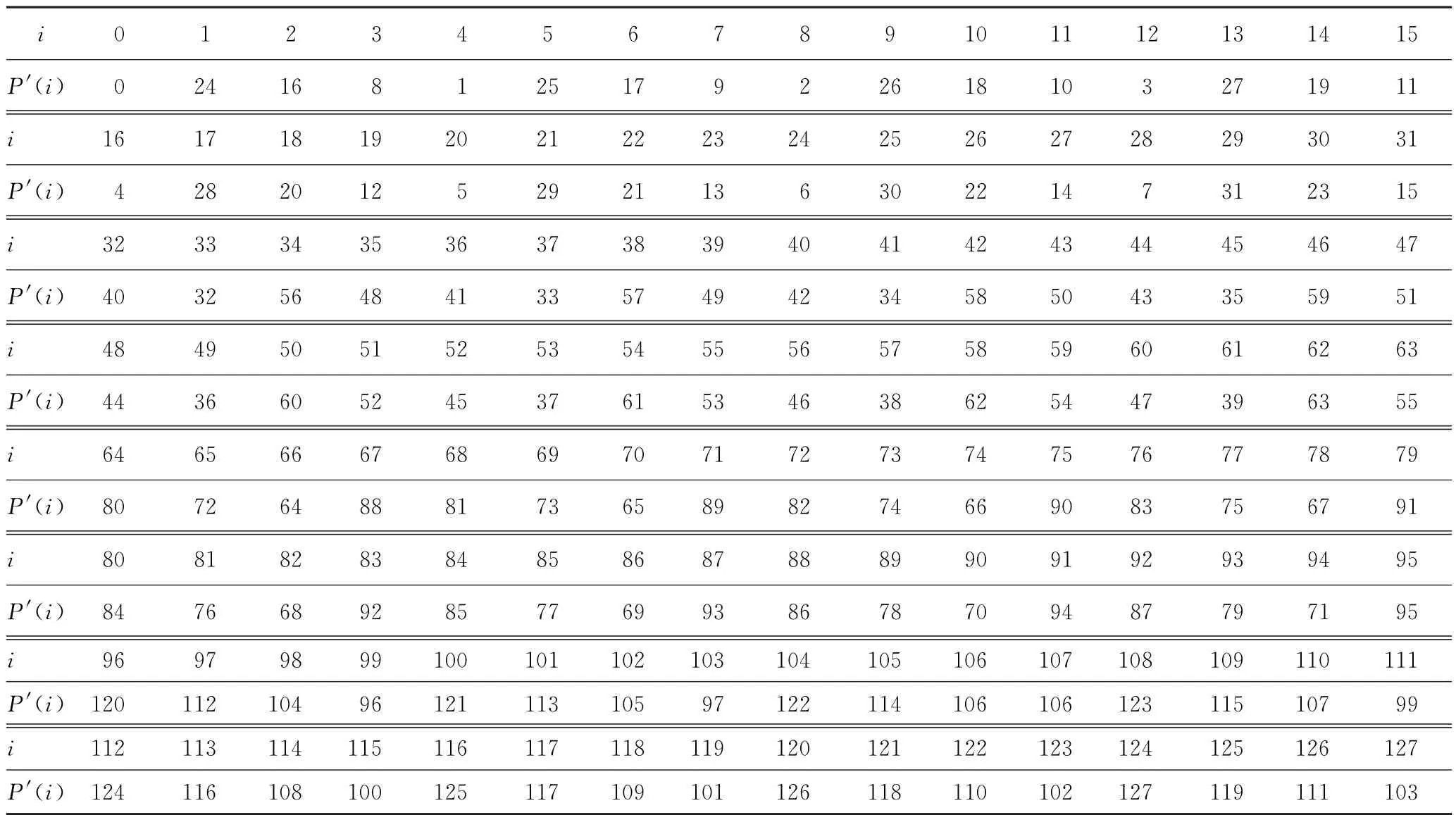
表1 横向混淆后的比特置换

4) 轮常量加实现。

对于轮常量C=c6c5c4c3c2c1c0,算法选择了127、23、19、15、11、7、3这7个比特位,除第127个比特位,其余比特位于新的中间状态的第3 和7 个S中,

其中:XY=00c5c4c3c2c1c0;Sa|Sb表示2个中间状态的拼接,第127 个比特位直接与S31的最高位异或。

3.2 引入线性码对S盒进行纠错检错

3.2.1 线性码的选择与生成

在实现具体的纠错检错方案前,需要先确定纠错码的防护能力及实现方式。

考虑2种攻击模型,即基于原始实现单个半字节的攻击和基于原始实现多个半字节的攻击。

1)基于原始实现单个半字节的攻击。攻击者对原始的1个S盒和对应冗余的4个比特位进行攻击。这些比特位分别位于不同的半字节中,因此,为冗余实现的各个4比特码字添加单比特纠错机制,实现半字节以下攻击的自动纠错能力。此时,线性码需要具备1 bit的纠错能力。

2)基于原始实现多个半字节的攻击。攻击者同时攻击左边2个或以上的半字节,并对冗余实现对应每个半字节中的多个比特攻击。若通过纠错实现安全性,会增加大量的冗余位,极大增加实现消耗。因此,对于需要纠错大于单比特的防护,根据引理2,防护方案采用检错与纠错并行的方式来降低过大的实现代价,选择的线性码需具备4 bit的检错能力。

综上,本方案需要实现一个单比特的纠错和4 bit的检错能力,根据1.3节可知线性码的最小距离为6,即需要找到一个[10,4,6]线性码。采用随机的方式获取线性码,随机生成一个矩阵4×10的矩阵G,遍历所有可能的信息码对应的线性码的汉明重量是否小于等于6(引理1),若有一个大于,则重新生成矩阵G并验证,否则表示生成成功。实验方案最终选择式(4)所表示的生成矩阵G。

根据生成矩阵G和定义2,容易获得校验矩阵H,如式(5)所示。

3.2.2 线性码纠错检错具体实现步骤

引入线性码为S盒提供纠错检错能力的具体步骤如下。

1)横向混淆实现进入S盒前,采用以下操作:

(a)为32个S盒的输入值Mi,计算冗余值Ri=Mi·G;

(b)保存所有的冗余值Ri。

2)S盒计算完成后,采用以下操作:

(a)将此时的S盒输入值与对应冗余值Ri组合生成一个10 bits待检测向量Di=|Ri;

(b)计算校验值Ci=H·Di;

(c)判断Ci是否等于0;

(d)若Ci等于0,表示无故障注入,结束检测模块,继续执行算法;

(e)若Ci不等于0,表示故障被注入,执行(f);

(f)比较Ci与校验矩阵H的第j列(1≤j≤4)Hj是否相等;

(g)若Ci=Hj,表示输入值Mi'第j个比特被注入故障,翻转第j比特进行纠错,重新执行当前轮函数;

(h)若均不相等,表示注入的故障大于单比特,无法纠错,输出空密文。

4 实验结果

对上述防护方案进行安全性测试。具体实验环境为:一台PC 机(Intel(R) Core(TM)i5-4200U CPU@1.6 GHz,8 GiB内存,Windows 7旗舰版);Microsoft Visual Studio 2019编译;故障的诱导采用半字节随机生成和固定比特位的随机生成2种方式进行模拟仿真。

4.1 抵抗差分故障攻击的有效性

攻击方法是在原始实现的中间状态找到一个或多个半字节进行注入错误,并对冗余实现对应的比特位进行攻击。

设定选择的明文为0x0102030405060708090a0b0c0d0e0f,主密钥为0x00000000000000000000000000000000。如表2所示,测试实验在不同轮数注入了不同的故障,共进行了100万次的随机故障注入测试,发现对于原始实现小于半字节的故障均可纠错,而对于原始实现大于半字节的故障也可以纠错,证明了防护方案的有效性。

表2 部分模拟攻击实验数据

4.2 方案性能(分析与比较)

对防护方案所需的软件消耗进行测试,发现新防护方案仅需额外25.08%的实现消耗。

本防护方案与现有技术对比如表3所示。

表3 差分故障攻击的防护性能对比

本研究和文献[15]由于利用了纠错码,相较其他防护方案增加了自动纠错的功能;文献[22]需要根据算法的轮函数特点,将各种操作合并成一张表,不具有可移植性。文献[12]减少了不必要的冗余信息,但自动纠错能力差。由于DEFAULT其轮数相对其他轻量级算法有所增加(DEFAULT有80轮),移植本防护方案到其他分组密码需要额外约25.08%×(80/40)×(40/28)≈72%的实现消耗。相较文献[22]的防护方案,本方案有显著的性能提升,并能提供半字节的自动纠错能力和全部比特位的检错能力。

5 结束语

在构造抵抗差分故障攻击的防护方案时,如何做到方案有效且额外消耗少是设计中的难点。基于DEFAULT密码的算法结构,利用横向混淆和线性码提出了一种新的防护方法:对DEFAULT 的第2个LAYER层使用横向混淆完成冗余部分的实现;此外,为了对每个比特位提供故障注入的检测能力,将具有1 bit纠错能力和4 bit检错能力的[10,4,6]线性码引入防护中。实验结果表明,新的防护方法在仅需要25.08%的额外软件性能消耗下,实现了抵抗多重故障注入攻击的能力。与已有防护方法相比,新的防护方法除了能有效地提供纠错及检错能力外,需要的实现代价更少。