大跨斜拉桥基于索力的结构损伤识别研究
2023-10-22于虹
于 虹
(1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063; 2.中国铁建股份有限公司桥梁工程实验室,湖北 武汉 430063)
0 引言
斜拉桥在服役过程中,由于荷载作用、材料老化和环境因素的作用,会出现拉索锈蚀、主梁及主塔开裂、螺栓松动等病害,造成结构性能退化[1]。因此,及时对斜拉桥结构的损伤进行检测和修复,对保障桥梁结构的安全服役具有重要意义[2-3]。
斜拉索是斜拉桥的主要承重构件之一,其受力状态是衡量斜拉桥是否处于正常状态的重要参量。斜拉桥结构主梁损伤会引起恒载内力重分布,从而引起斜拉索索力变化,因此可以利用斜拉索索力变化识别斜拉桥主梁损伤。孙宗光[4]首次探讨了基于斜拉索张力指标与人工神经网络技术相结合,对斜拉桥主梁中的损伤进行定位识别。朱浩等[5]根据斜拉桥主梁的线形由于斜拉索索力的改变而改变这一规律,通过对主梁位移的改变量进行反演,得到索力的变化情况,从而对斜拉桥的内力状态进行识别。Hua[6]利用斜拉桥主梁损伤前后的索力变化,通过构造斜拉桥主梁参数对斜拉索索力的灵敏度矩阵,结合模型修正技术对斜拉桥的主梁进行损伤识别。李延强等[7]基于斜拉桥主梁损伤对索力的敏感性分析,选择一组四根(空间位置对称)对主梁损伤最敏感的斜拉索索力构造损伤指标,利用BP 神经网络对斜拉桥有限元模型中的主梁损伤进行识别。
该文利用斜拉索索力作为损伤敏感指标,并分析计算斜拉索索力对结构损伤的灵敏度,据此对高速铁路大跨度斜拉桥结构中的损伤进行识别分析。以裕溪河特大桥为研究对象,对所提出方法的有效性和准确性进行验证。
1 斜拉索索力对主梁损伤灵敏度分析
1.1 灵敏度分析理论
灵敏度分析主要是研究系统输入x的变化会导致系统响应量g如何变化的问题。当系统的输入发生变化时,系统的响应量也将会随之发生改变,这种改变的相对程度就称为系统响应量g对于系统输入变量x的灵敏度,可以用偏微分∂g/x∂ 表示。
有限差分法的原理是利用差商近似微商,可以表示为
1.2 斜拉索索力对主梁损伤灵敏度计算
在结构损伤识别研究中,通常假设结构的质量在损伤发生时不发生变化,通过结构单元刚度的变化来模拟结构损伤。假设斜拉桥结构主梁第j个单元的刚度参数(如抗弯刚度)由折减至损伤状态的,则第j个单元的刚度折减系数(Stiffness Reduction Factor,SRF)可以定义为
式中,ne——斜拉桥结构主梁中单元的个数。刚度折减系数jγ的取值范围为-1~0。
该文通过折减有限元模型中结构单元的弹性模量,实现对结构损伤的模拟。利用MATLAB 调用ANSYS,计算斜拉索索力对斜拉桥主梁损伤的灵敏度矩阵,具体步骤如下:
(1)计算健康状态下裕溪河特大桥在恒载作用下的斜拉索索力向量F0。
(2)保持其他参数不变,利用MATLAB 调用ANSYS,依次令第j个主梁结构单元发生1%刚度折减(γj=-0.01),计算此时恒载作用下的斜拉索索力向量。
(3)基于有限差分理论,利用公式(1)计算斜拉索索力对第j个主梁结构单元损伤的灵敏度。
(4)重复步骤(2)和(3),计算斜拉索索力对所有主梁结构单元损伤的灵敏度,得到斜拉索索力对主梁损伤的灵敏度矩阵。
2 基于斜拉索索力的损伤识别方程
基于斜拉索索力变化的损伤识别方程可以表示为
式中,[S]——斜拉索索力对结构损伤的灵敏度矩阵;{FD}——通过测量得到的结构损伤状态的斜拉索索力;{F0}——通过测量得到的未损伤状态的斜拉索索力。解向量γ中的非零元素对应的单元编号反映损伤的位置,非零元素的大小反映损伤的程度。
3 基于稀疏正则化的结构损伤识别
在实际工程中,通过测量获取的斜拉索索力向量中元素的个数通常要远小于未知结构单元刚度参数的个数。因此,公式(3)通常为欠定方程组,有无穷多个可能的解,不满足适定性问题解的唯一性,即公式(3)的求解是一种不适定问题。正则化算法是求解不适定问题的有效方法,它利用具体问题的某些附加信息,通过一个近似的适定性问题去寻找原不适定问题的近似解。稀疏正则化是指在优化问题的求解过程中,将l1范数引入目标函数,使解向量具有稀疏性。
结构损伤通常只发生在整个结构的一小部分构件中,即损伤向量具有稀疏性。基于这个先验知识,可以在公式(3)的求解过程中引入对解向量γ的稀疏约束,将公式(3)转换为一种约束优化问题P1:
问题P1等价于如下的稀疏正则化问题:
式中,J——稀疏正则化问题的目标函数;τ——正则化参数。
对于稀疏正则化问题,当正则化参数的取值达到一定限值时,问题的解收敛于零,即解中元素全为零。正则化参数τ的最大值可以表示为
该研究提出的大跨斜拉桥基于索力的结构损伤识别流程如图1 所示。首先,选取斜拉索的索力作为损伤敏感指标,并利用有限差分法计算斜拉索索力对结构损伤的灵敏度;然后,建立一个由结构刚度折减系数和损伤前后斜拉索索力组成的欠定方程组;最后,使用稀疏正则化算法对欠定方程组进行求解,解向量中的非零元素表示结构损伤的位置和程度。
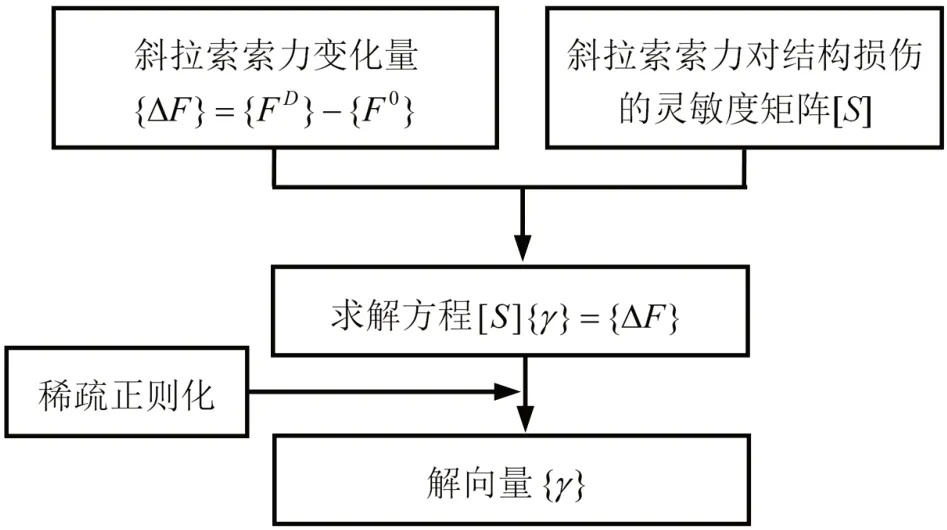
图1 大跨斜拉桥基于索力的结构损伤识别流程
4 数值模拟算例
4.1 裕溪河特大桥简介
商丘至合肥至杭州铁路裕溪河特大桥主桥采用(61+120+324+120+61)m 双塔钢箱桁梁斜拉桥方案,全长686 m。以裕溪河特大桥为研究对象,对所提出损伤识别方法的精度和有效性进行验证。裕溪河特大桥全桥立面布置如图2 所示。

图2 裕溪河特大桥全桥立面布置示意图(m)
大桥主梁为钢箱桁结构,桁架采用不带竖杆的华伦式桁架,下弦采用整体式钢箱梁,如图3 所示。
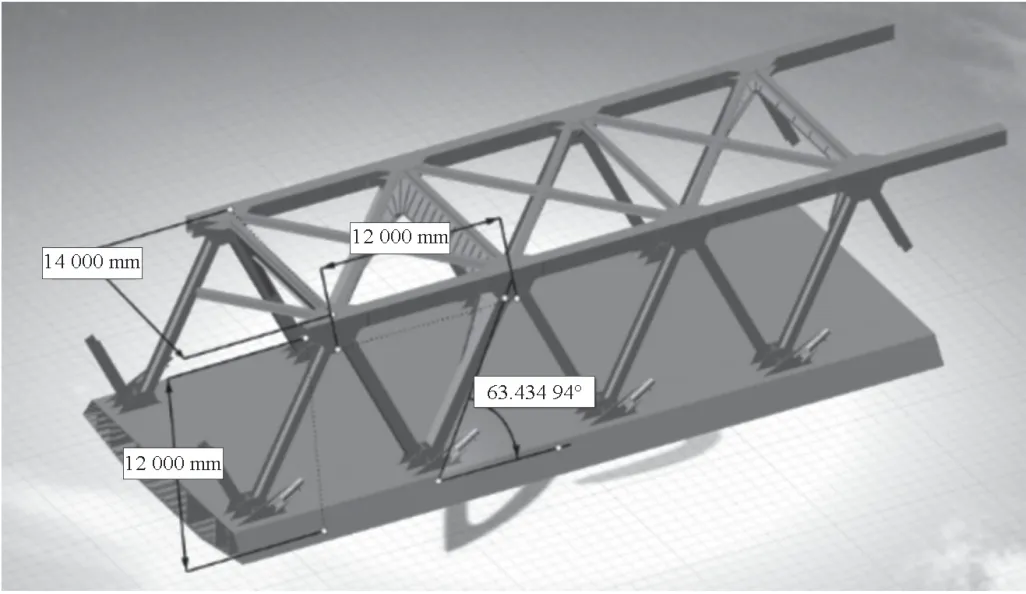
图3 裕溪河特大桥主梁结构示意图
4.2 斜拉索索力对主梁损伤灵敏度矩阵
裕溪河特大桥主梁为组合钢箱桁梁,该文以箱梁发生损伤的情况为例,对基于索力的大跨斜拉桥结构损伤识别过程进行说明。裕溪河特大桥斜拉索为空间双索面,立面上每塔两侧共13 对索,全桥共104 根斜拉索。对每根斜拉索单独进行编号,如图4 所示。按照在商丘至杭州方向线路中心线的左侧或右侧,将全桥斜拉索分为左侧索面和右侧索面。对于左侧索面,斜拉索自商丘至杭州方向依次编号为1~52;对于右侧索面,斜拉索自商丘至杭州方向依次编号为53~104。

图4 裕溪河特大桥斜拉索编号简图
将裕溪河大桥主梁箱梁按照节间划分为57 个梁段,对每个梁段单独进行编号,自商丘至杭州方向依次编号为1~57,如图5 所示。

图5 裕溪河特大桥箱梁编号简图
将箱梁的每一个梁段看作一个损伤位置,依次计算每一个梁段发生1%刚度折减时的斜拉索索力,基于有限差分理论可以得到斜拉索索力对箱梁损伤的灵敏度矩阵,如图6 所示(为方便展示,取绝对值)。

图6 斜拉索索力对箱梁损伤的灵敏度矩阵(绝对值)
4.3 损伤工况
为了研究所提出的损伤识别方法是否对结构中不同位置的损伤敏感,从箱梁结构中选取具有代表性的4 个箱梁单元进行损伤识别分析,所选取的4 个箱梁单元的编号分别为3、9、22 和28,箱梁编号如图5 所示。一共模拟6 种箱梁结构损伤工况,包含4 种单损伤工况和2种多损伤工况。各损伤工况具体配置如表1 所示。

表1 箱梁结构损伤工况
4.4 损伤识别结果
利用损伤前后斜拉索索力变化和斜拉索索力对箱梁损伤的灵敏度,可以建立如公式(3)所示的求解方程。使用稀疏正则化算法对公式(3)进行求解,得到各损伤工况的刚度折减系数SRF。
箱梁结构单损伤工况的损伤识别结果如图7 所示。从图中可以看出,在实际损伤位置处,刚度折减系数SRF 的识别值十分明显,而其他位置处刚度折减系数SRF 的识别值为零或者接近零。并且,3、9、22 和28号腹杆处刚度折减系数SRF 的识别值分别为-0.312、-0.307、-0.336 和-0.319,与实际值-0.3 吻合较好。以上结果表明,所提出的损伤识别方法能够准确识别裕溪河特大桥箱梁结构中不同位置的损伤,并且识别出的损伤程度接近实际损伤程度。
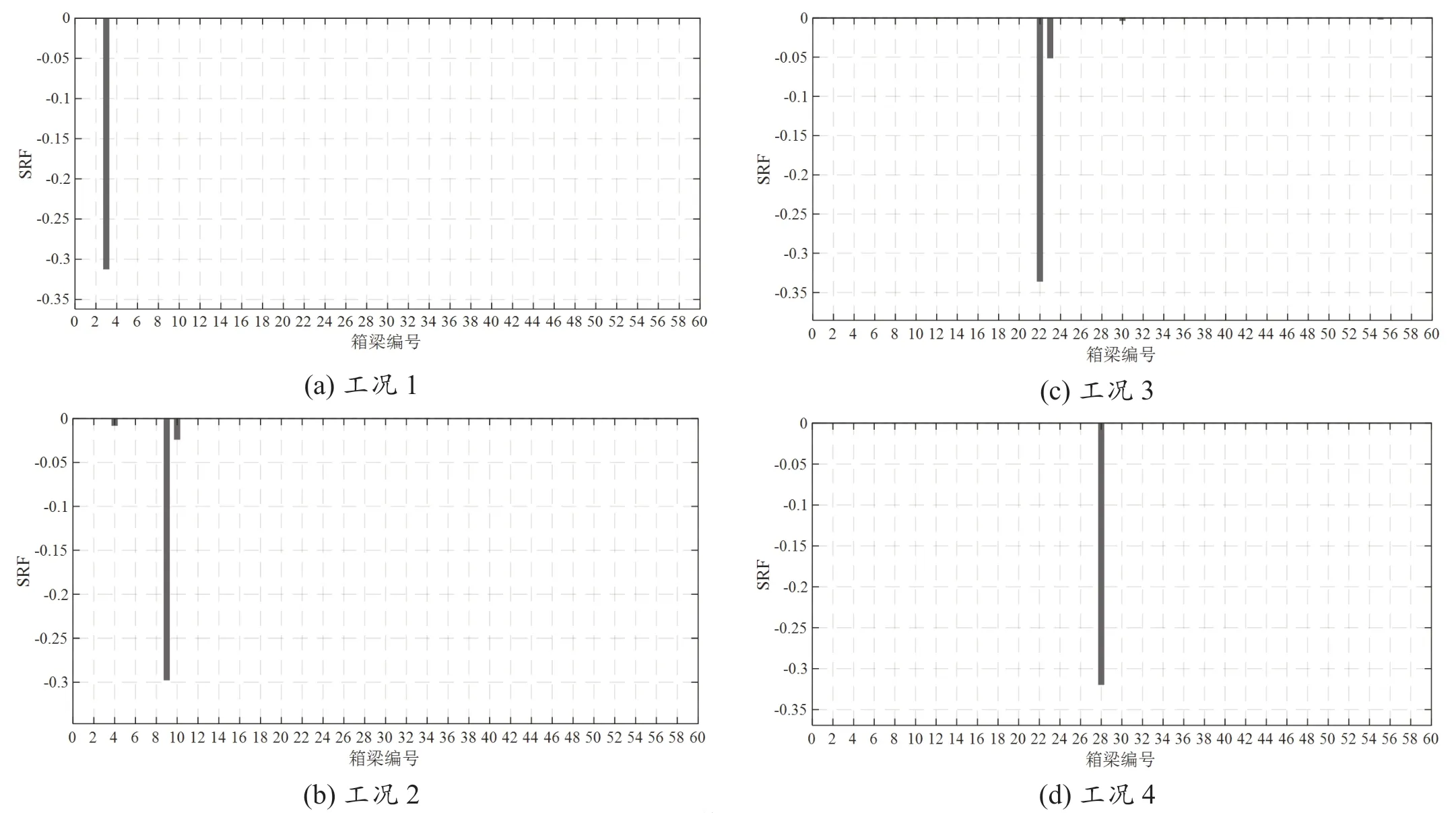
图7 单损伤工况识别结果
箱梁结构多位置损伤的识别结果如图8 所示。从图中可以看出,在实际损伤位置处,刚度折减系数SRF 的识别值十分明显,而其他位置处刚度折减系数SRF 的识别值为零或者接近零。对于工况5,3 号箱梁单元处刚度折减系数SRF 的识别值为-0.414,与实际值-0.3一致;22 号箱梁单元处刚度折减系数SRF 的识别值为-0.347,与实际值-0.3 接近。对于工况6,9 号箱梁单元处刚度折减系数SRF 的识别值为-0.336,与实际值-0.3 接近;28 号箱梁单元处刚度折减系数SRF 的识别值为-0.408,与实际值-0.3 一致。以上结果表明,所提出的损伤识别方法可以正确识别裕溪河特大桥箱梁结构中多个位置同时发生的损伤,并且识别出的损伤程度与实际损伤程度一致。

图8 多损伤工况识别结果
5 结论
为了识别斜拉桥结构中的损伤,该文提出了一种基于索力的大跨斜拉桥结构损伤识别方法。针对裕溪河特大桥数值模型的计算结果表明,所提出的损伤识别方法可以正确识别裕溪河特大桥桁架和箱梁结构中的单位置损伤和多位置损伤,并且识别出的损伤程度与实际损伤程度一致。
