赛博攻击下韧性系统的动力学特性研究

吴怡淳 闫晶晶 丁冉 唐异垒

(1.上海交通大学数学科学学院,上海,200240;2.信息系统工程重点实验室,南京,210023;3.中国电子科技集团公司第二十八研究所,南京,210023)

1 引言

随着信息和网络技术的飞速发展,以计算机病毒传播为主的赛博攻击对新一代韧性系统的能力提出了更高的要求.韧性系统是在继承和发展共用信息基础设施的基础上,引入新的理念、模式和技术等,使自身具备更加灵活、适变和抗毁等韧性能力特征的系统[30,31].一旦计算机病毒传播到一个大规模的韧性系统中,为了确保系统的体系防控能力能有效生成,韧性系统必须具备保持或快速恢复正常服务的能力.

计算机病毒的感染传播是复杂的,它的动力学行为常常被类比成经典的传染病模型,只是计算机病毒能在几秒之内在网络中广泛传播并造成破坏[1,4,16].遭受赛博攻击后,如果计算、存储、网络以及关联的信息和服务异常,将严重影响系统完成核心任务的能力.关于韧性系统的研究,主要关注系统在遭受赛博攻击后,能否具有保持或快速恢复正常服务的能力,包括: 适应能力、吸收扰动能力、恢复能力等[30,31].另外,来自外部的扰动也可能导致系统各项性能下降,此时韧性系统能否恢复到扰动前的性能水平,也是关注的要点,由此产生“韧性三角”的概念(参见图1).

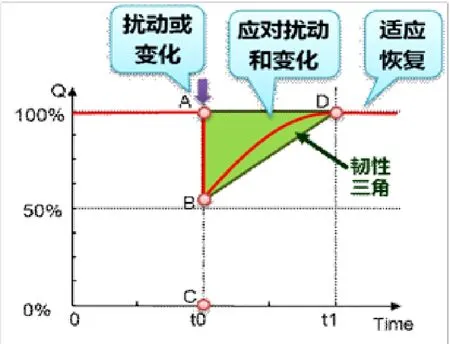
图1 韧性三角概念图

我们研究发现,病毒攻击系统也具有韧性系统的特性.系统动力学性态的研究主要包括以下几个方面: 在突发的扰动或者变化时能否保持稳定;对扰动或者变化系统是否能够自我修复与恢复;能否抵抗抗干扰;在关键因素临界点(分岔点)是否脆弱,能否保持结构稳定等.上述研究内容在韧性系统领域也非常重要且广受关注.因此,我们把动力系统与韧性系统结合起来考虑,运用传播动力学的机理来建立模型,运用动力学的方法来进行理论分析,并把所得的结果用于韧性系统的能力分析与解释.

经典的传播动力学模型源于对传染病的研究,在研究疾病起因,预测传染病的发展趋势,探索科学防控上起到重要作用.以经典的SIS,SIR 仓室模型为基础,研究发展过程中传播动力学结合微分方程定性与分岔理论,将方程向高维推进,得到了更符合真实情况的精细化、多元化、复杂化的模型.

在传统的传染病模型动力学研究中,基于不同的方法建立了多种类型的模型.为探索计算机病毒的传播动力学,Cohen[3],Murray[23]及以后的学者,将计算机病毒分为susceptible(S),infectious(I),recovered(R),antidotal(A),breaking out(B),exposed(E),latent(L),quarantined(Q) 和vaccinated(V) 等不同状态.自从Kephart 和White[13,14]建立有向图模型并提出一些量化检测方法后,人们建立了多类韧性动力学模型来刻画流行病模型在网络中的动力学传播机理,例如: SIR 模型[10,19,24],SIRS 模型[9,22,26,33],SEIR 模型[7,32],SEIRS 模型[20,21],SLBS 模型[8,28,29],SLIR 模型[11],SAIR 模型[12,25],SLBQRS 模型[15]和SEVIR 模型[27]等.

在以往的文献中,全局稳定性的证明常常依赖于构建Lyapunov 函数的方法.但是此类方法不具有一般性且技巧性很强,在高维微分方程的研究中难以推广.本文在研究过程中证明两种平衡点的局部和全局渐近稳定性,为此类问题的研究提供了新的思路和方法.

本文余下的部分安排如下: 第二节构建赛博击下韧性系统的模型;第三节在计算基本再生数的基础上,分别证明无病毒平衡点和有病毒平衡点的存在性,定性分析韧性系统的局部动力学;第四节致力于韧性系统全局动力学的研究;最后一节通过数值模拟研究和分析韧性系统的能力特征,包括: 适应能力、恢复能力、吸收扰动能力等.

2 基于病毒传播动力学原理的赛博攻击模型构建

在分布式拒绝服务攻击的框架下,考虑到病毒攻击的特殊性(例如DDos 病毒),我们建模时引入两种类型的网络节点: 攻击节点和目标节点.攻击节点发起病毒攻击,而目标节点承受攻击.然后我们再细分攻击节点和目标节点.攻击节点被划分为3 个舱室: 易感染舱室Sa(Sa也表示易感染仓室中所含的节点数,其他仓室亦如此),被感染舱室(Ia)和外部舱室(Ea).目标节点也被划分为3 个舱室: 易感染舱室(St),被感染舱室(It)和恢复舱室(Rt).其中,S表示易感节点(susceptible,S同时也表示易感节点的数目,下文的I,R,E亦如此),即还没被感染的节点,但与已感染节点一旦接触就可能会被感染;I表示感染节点(infective),即具有病毒传染力的节点;R表示已恢复节点(recovered),即已恢复正常的节点,这部分节点具有一定免疫或者防护能力;E表示外部节点(exposed),即和攻击者脱离连接,进入断线状态而不能参与感染或被感染的攻击节点;详细的变量符号及含义见表1.

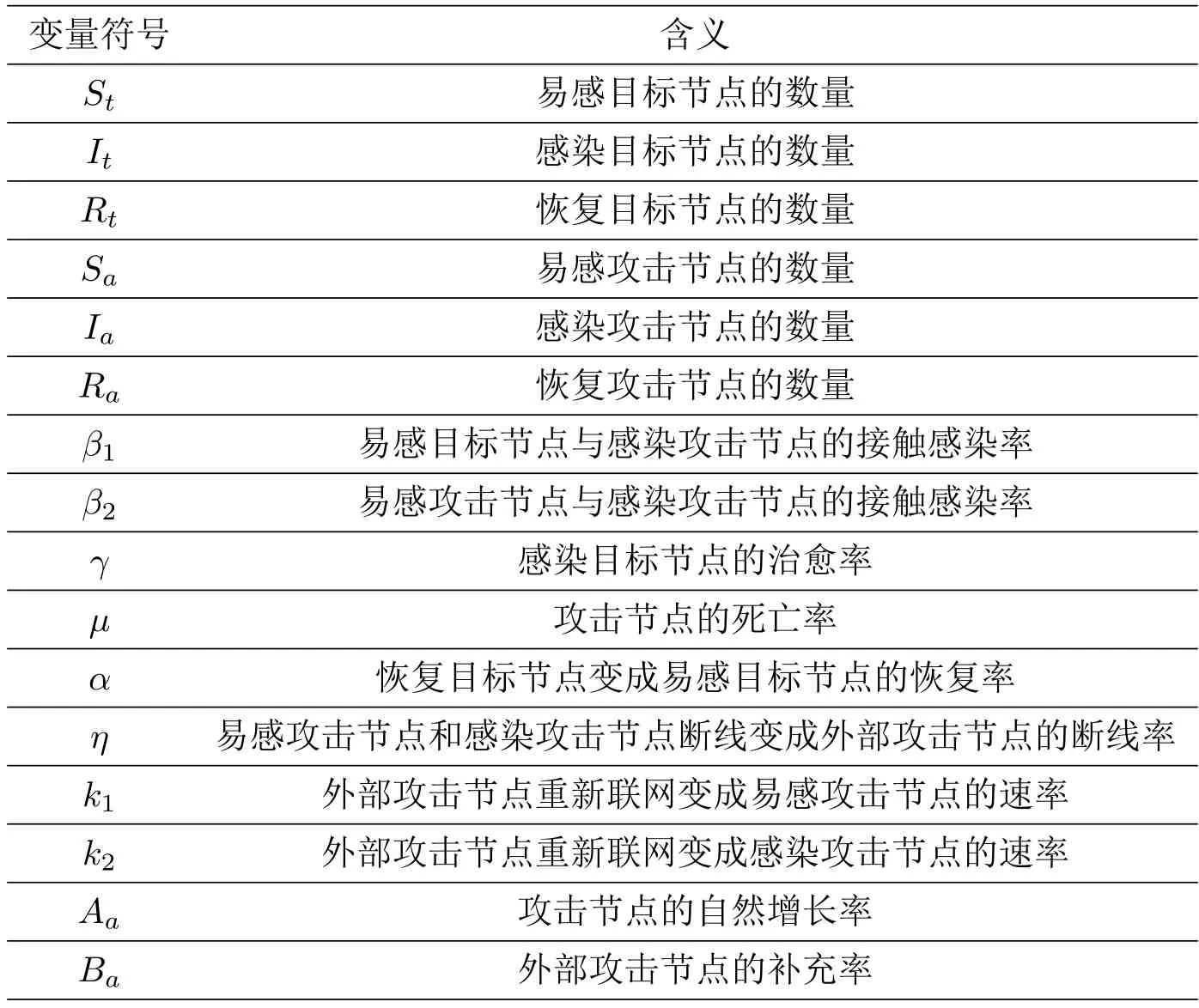
表1 变量与参数标注

记攻击和目标节点的总数分别为Na和Nt,即

我们对这个模型作一些基本假设:

1.目标节点全程都不参与到主动攻击的行动中,因为攻击者总是意欲俘获尽可能多的感染主机并加强攻击强度;

2.目标节点数在这个感染过程中恒定,不出现崩坏和自然增长现象;

3.易感目标节点与感染攻击节点的接触概率采用标准接触率,即β1StIa/Na,其中β1为正常数;

4.恢复节点的恢复速率为一常数,且恢复以后的节点将进入易感者舱室,对于计算机病毒无免疫作用;

5.所有攻击节点的崩坏率也为一个正常数;

6.在攻击节点中,易感节点具有一定的自然增长率Aa,而外部节点中也有节点数的补充,补充率为Ba,这里Aa和Ba均为常数.

在这些假设下,对目标节点我们有:

1.易感者进入感染者舱室的速率为β1StIa/Na,其中β1＞0 为常数;

2.感染者得到恢复而进入恢复舱室的速率为γ ＞0;

3.恢复者无法获得永久性免疫,以速率α回到易感者舱室,其中α ＞0 为常数.

对攻击节点有:

1.易感者被感染而进入感染者舱室的速率为β2StIa/Na,与攻击者断线而进入外部舱室的速率为η,其中η ＞0,β2＞0 为常数;

2.感染者攻击目标易感节点,但自身与攻击者断线而进入外部舱室的速率也为η;

3.外部节点重新联网并分别转入易感者和感染者的概率分别为k1＞0 和k2＞0;

4.各攻击节点中的电脑崩坏率为µ＞0.

图2 直观地描述了上述感染过程.

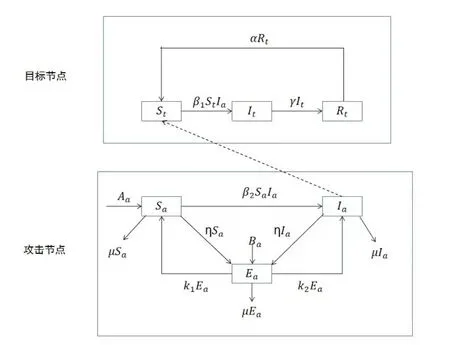
图2 感染过程概要图

在上述假设下,对于目标节点,有:

对于攻击节点,有:

上述模型可通过变换进行简化.

可得

量记号即可得到如下的四维系统:

该系统的一个正向不变锥域(可行域)为:

3 韧性系统的局部动力学分析

韧性系统在遭受赛博攻击后的应对可划分为三个阶段: 抵御阶段、生存阶段和恢复阶段,其中,抵御阶段指系统在未遭受扰动时处于正常运行状态的阶段,生存阶段是指系统吸收外部扰动的阶段,恢复阶段是指系统能力恢复与再生的阶段.下面我们运用动力学原理对韧性系统遭受赛博攻击后的局部稳定性进行分析.

3.1 平衡点与基本再生数

我们应用[2,5,6]中的方法计算基本再生数,具体过程如下.

令(2.3)各式右端项为0,可以得到无病毒平衡点E0(1,0,0,0),且此时有

利用下一代矩阵法,构建矩阵F和V:

代入无病毒平衡点E0(1,0,0,0)可得:

故可得基本再生数

3.2 局部稳定性分析

定理3.1当R0＜1 时,系统(2.3)的无病毒平衡点E0(1,0,0,0)局部渐近稳定,而当R0≥1时，E0(1,0,0,0)不稳定.

证明系统(2.3)在平衡点的Jacobi 矩阵为:

故在无病毒平衡点E0(1,0,0,0)处的Jacobi 矩阵为:

JE0的特征值为:

因此,当R0＜1 时,所有的特征值实部都小于0.由Hurwitz 判据可知,此时无病毒平衡点是局部稳定的.而当R0＞1 时,存在具有正实部的特征值,故此时无病毒平衡点是不稳定的.

下面用中心流形理论证明当R0=1 时,E0(1,0,0,0)是不稳定的.

易知λ1,λ2,λ4均为负实数,λ3=0,故此时E0为非双曲平衡点,且λ1,λ2,λ4对应相空间的稳定子空间和稳定不变流形,λ3对应相空间的中心子空间和中心流形.

记上述方程组线性部分的矩阵为A,非线性部分的矩阵为B.则存在可逆矩阵

使得:

其中L=1+η+k1+k2.

令Y=PZ,可得

即

其中,

令各项系数为0,可得z4=h3(z3)=0.

及

化简得

解得

故h1(z3),h2(z3)的泰勒展开二阶项系数都为负.最后可得,中心流形上的方程为

由二次项系数不为0 知,原点处的中心流形不稳定.故当R0=1 时,平衡点E0(1,0,0,0)是不稳定的.

定理3.2当R0＞1 时,系统(2.3)的有病毒平衡点是局部渐近稳定的.

证明应用中心流形定理及定理3.1,我们可以得到在R0＞1 时平衡点E0(1,0,0,0)是不稳定的,且轨道是有界的,均位于正向不变集D区域内.

4 韧性系统的全局动力学分析

相对于局部稳定性,韧性系统的全局稳定性需要更强的条件来证明.我们将系统重写为

其中S∈Rm表示系统中未受感染的易感者数,I∈Rn表示系统中的其他变量.记(4.1)的无病毒平衡点为

我们应用文献[2]中的判定方法来证明无病毒平衡点的全局稳定性.

引理4.1([2])对于系统(4.1),以下结论成立:

由引理4.1,我们可得到下面的定理.

定理4.1当R0＜1 时,系统(2.3)的无病毒平衡点是全局渐近稳定的.

证明记无病毒平衡点为E0=(S0,0,0,0),其中S0=1.考虑方程

由F(S0,0)=0 且F(S,0)=α(1-S),可得

从而

当t→∞时,S→S0.故系统(2.3)是全局渐近稳定的,且(C1)成立.

再设I=(It,Ia,Ea)T.考虑方程

其中

显然,每个非对角元都是非负的,故A是一个M阵.再由

综上可知,引理4.1中的(C1),(C2) 都成立,从而系统(2.3) 的无病毒平衡点E0(1,0,0,0) 在R0＜1 时全局渐近稳定.

证明我们利用高维Bendixson 判据[17,18]来证明这个定理.在以下条件具备时去讨论全局稳定性.

二维时的散度为Jacobi 矩阵的对角元之和,我们需要给出高维时的散度,故引入第二加性复合矩阵并计算Lozinskii 测度.

首先,系统在有病毒平衡点处的Jacobi 矩阵为

由字典顺序(1)=(1,2),(2)=(1,3),(3)=(1,4),(4)=(2,3),(5)=(2,4),(6)=(3,4),可得第二加性复合矩阵

其中,

然后,我们来计算Lozinskii 测度.为此,构造一个6 维对角方阵:

易得,

将其写成如下分块矩阵形式:

其中,

设µ为L1矩阵范数诱导的Lozinskii 测度.令

由(2.3)可得

5 数值模拟及韧性分析

本节将通过Matlab 仿真来模拟计算机病毒传播的动力学过程以及韧性系统的稳定性.

首先我们验证当R0＜1 时,无病毒平衡点的全局稳定性.

设定参数:α=0.3,β1=0.8,β2=0.02,γ=0.03,η=0,k1=0.2,k2=0.4,Aa=10,Ba=0.此时,可得

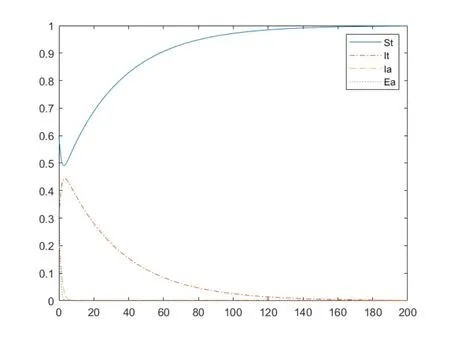
图3 X0=(0.6,0.3,0.2,0.5),R0＜1

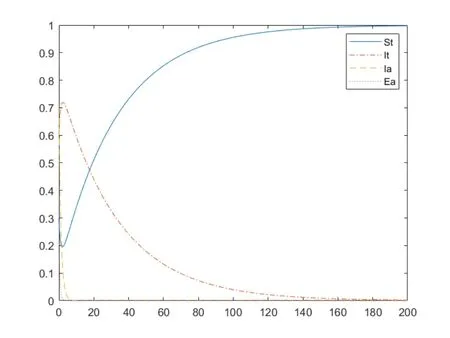
图4 X0=(0.3,0.6,0.7,0.2),R0＜1

可以看到,当选取不同的初值时,在R0＜1 的情形下,无病毒平衡点具有全局稳定性.这体现了韧性系统的适应能力和恢复能力.

接下来我们考虑当R0＞1 时,有病毒平衡点的全局稳定性.设定参数:α=0.4,β1=0.4,β2=0.04,γ=0.03,η=0.4,k1=0.2,k2=0.4,Aa=100,Ba=3.此时,

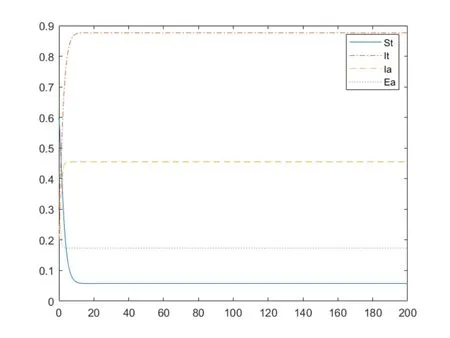
图5 X0=(0.6,0.3,0.2,0.5),R0＞1

图6 X0=(0.3,0.6,0.5,0.2),R0＞1

二者相差极小.随着t的增大,系统显然具有全局稳定性,这也体现了韧性系统的适应能力、恢复能力和吸收扰动能力.

最后,我们检验在R0=1 这一临界情形下,无病毒平衡点的稳定性.设定参数:α=0.4,β1=0.4,β2=0.01,γ=0.03,η=,k1=0.2,k2=0.4,Aa=100,Ba=0.此时

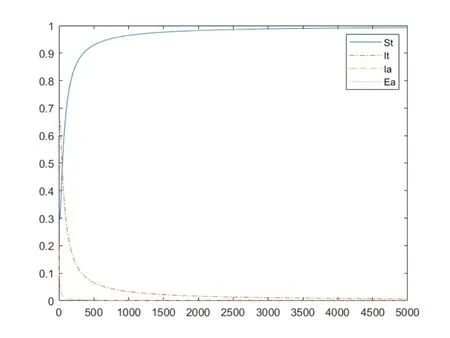
图7 X0=(0.6,0.3,0.2,0.5),R0=1

图8 X0=(0.3,0.6,0.6,0.2),R0=1