The Extremal p-spectral Radii of Trees,Unicyclic and Bicyclic Graphs with Given Number of Segments

Qiu Mairong He Xiaocong

(School of Mathematics and Statistics,Central South University,Changsha 410083,China)

Abstract Let G be a finite and simple graph.A walk S is called a segment of G if the endpoints(not necessarily distinct)of S are of degree 1 or at least 3,and each of the rest vertices is of degree 2 in G.In this paper,we determine the graphs that maximize the p-spectral radius for p ＞1 among trees,unicyclic and bicyclic graphs with given order and number of segments,respectively.

Key words p-spectral radius Tree Unicyclic graph Bicyclic graph Segment

1 Introduction

Assume all graphs in this paper are finite and simple.LetGbe a graph with vertex setV(G)={v1,v2,···,vn} and edge setE(G).We follow the notation and terminologies in [1] except otherwise stated.If two verticesviandvjare adjacent,we writevi～vj,otherwise,writevi≁vj.The adjacency matrix ofGis defined asA(G)=(aij)n×nwhereaij=1 ifvi～vj,andaij=0 otherwise.LetdG(vi)be the degree ofviandNG(vi)be the set of neighbors ofviinG.As usual,denote by Δ(G)the maximum degree inG.The distance between two verticesuandv,denoted byd(u,v),is the length of a shortest path betweenuandv.IfHis a subgraph ofG,letd(u,H)=min{d(u,v)|v ∈V(H)}.

Denote byPnandCnthe path and the cycle onnvertices,respectively.kpathsare said to have almost equal lengths if|li-lj|≤1 for 1≤i,j ≤k.A vertex of degree 1 in a graph is said to be a pendant vertex and a vertex of degree at least 3 is called a branching vertex.An induced path with verticesu1,u2,···,utis called a pendant path ofG,ifdG(u2)=···=dG(ut-1)=2 anddG(ut)=1(note that there is no requirement on the degree ofu1).A walk is a sequence of verticesu1,u2,···,ukofGsuch thatui-1～uifori=2,···,k,where the first vertexu1and last vertexukare called endpoints.A walkSis a segment of a graph if the endpoints(not necessarily distinct)ofSare of degree 1 or at least 3,and each of the rest vertices is of degree 2 in the graph.

fork=1,2,···,n,which is called the eigenequation ofλ(p)(G)for the vertexvk.

Thep-spectral radiusλ(p)(G) is a multifaceted parameter,asλ(1)(G)/2 is the Lagrangian ofG(see [19]).Especially,λ(2)(G) is the usual spectral radius introduced by Cooper and Dutle [4],and limp→∞λ(p)(G)=2|E(G)|(see[17]).The investigation on the spectral radius of graphs is an important topic in the theory of graph spectra.Recently,the problem concerning graphs with maximal or minimal spectral radius of a given class of graphs has been studied extensively.Brualdi and Solheid [2] studied the spectral radius of connected graphs.Guo[7]determined graphs with the largest spectral radius among all the unicyclic graphs and all bicyclic graphs onnvertices andkpendant vertices,respectively.Lin and Zhou[13]obtained the structure of trees that maximize the distance spectral radius among trees with given order and number of segments.Lin and Song[16]considered the family of all trees with given number of segment sequences and proved that the generalized star minimizes the Wiener index.It should be noted that extremal problems forλ(p)(G)mainly focus on hypergraphs(see[4,5,8,9,11,17,18]).Kang,Liu,Lu and Wang [8] characterized the 3-uniform hypergraphs with maximump-spectral radius forp ≥1 among the Berge-Ghypergraphs whenGis a path,a cycle or a star.For more advances in research on spectral radius of graphs,we refer the readers to[3,6,7,12-15].

Letkbe the number of segments inGandℓbe the number of vertices of degree 2 inG.IfSis a segment ofG,we writeS ∈G.Denote the length of a segmentSbylSand the number of vertices of degree 2 inSbyℓS.It is easy to know that ∑S∈G lS=m(G)andℓS=lS -1.Then

Therefore,in the class ofc-cyclicn-vertex graphs,as long as the number of segments of graphs is given,the number of vertices of degree 2 is determined.Based on this observation,in this paper,we determine the structure of trees,unicyclic and bicyclic graphs attaining the maximump-spectral radius with given number of segments,respectively.

LetG(n,c,k),T(n,k),U(n,k)andB(n,k)be the set ofc-cyclic graphs,trees,unicyclic graphs and bicyclic graphs withnvertices andksegments,respectively.Obviously,T(n,1)=PnandT(n,0)=T(n,2)=∅;U(n,0)=CnandU(n,1)=∅;B(n,0)=B(n,1)=∅.Thus,we only need to consider trees inT(n,k)for 3≤k ≤n-1,unicyclic graphs inU(n,k)for 2≤k ≤n,bicyclic graphs inB(n,k)for 2≤k ≤n+1.

LetTn,kbe ann-vertex tree with exactly one branching vertex formed by identifying one end-vertex of each of thekpaths with almost equal lengths (see Figure 1 for it and all the following graphs).Let Δ(i,j,k)be ann-vertex unicyclic graph obtained fromC3by attachingi,jandkpendant vertices to each vertex ofC3,respectively.We writefor a unicyclic graph onnvertices obtained fromC3by attachingkpaths of almost equal lengths to one vertex.LetB*be a bicyclic graph with 4 vertices andB**be a bicyclic graph with 5 vertices and exactly one branching vertex.Letbe a bicyclic graph obtained by attachingkpendant paths of almost equal lengths to one vertex of degree 3 inB*.Letbe a bicyclic graph obtained by attachingkpendant paths of almost equal lengths to the vertex of degree 4 inB**.LetH1be attained fromB*by attachingk-7 pendant vertices to one vertex of degree 3 ofB*,and attaching a pendant vertex to the vertices of degree 2 inB*,respectively.LetH2be attained fromB*by attachingk-5 pendant vertices to one vertex of degree 3 ofB*,and attaching a pendant vertex to one vertex of degree 2 inB*.We can now state our main results.

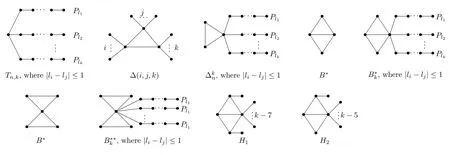
Figure 1 Some special graphs

Theorem 1.1Letp ＞1,3≤k ≤n-1 andT ∈T(n,k).Thenλ(p)(T)＜λ(p)(Tn,k),unlessTTn,k.

Our paper is organized as follows.In the next section,we study some edge-shifting operations for connected graphs,and consider the effect of them to increase or decrease thep-spectral radius.In Section 3,Section 4 and Section 5,we give the proof of Theorem 1.1,Theorem 1.2 and Theorem 1.3,respectively.

2 Preliminaries

In this section,we introduce some elementary lemmas and known results for comparing thep-spectral radius by edge-shifting operations.Firstly,we have the following results.

Lemma 2.2([8])Letp ≥1 andGbe a connected graph.Letu,vbe two vertices ofGandv1,v2,···,vs ∈N(v)N(u)(1≤s ≤dG(v)).Letx=(x1,x2,···,xn)Tbe a nonegative eigenvector ofλ(p)(G)with‖x‖p=1,wherexicorresponds to the vertexvi(i=1,2,···,n).LetG*be the graph obtained fromGby deleting the edgesvviand adding the edgesuvi,1≤i ≤s.Ifxu ≥xv,then

Furthermore,ifp ＞1,then

SupposeGis a connected graph anduis a vertex ofG.LetG(u;k,s)be the graph obtained fromGby attaching two pendant paths of lengthskandsatu,respectively.

Lemma 2.3([8])LetGbe a connected graph andu ∈V(G).Ifk ≥s ≥1,thenλ(p)(G(u;k,s))＞λ(p)(G(u;k+1,s-1))forp ＞1.

Supposea,bare two adjacent vertices ofGwithdG(a)≥2 anddG(b)≥2.LetG(1)(k,s)be the graph obtained fromGby attaching a pendant path of lengthkat vertexaand attaching a pendant path of lengthsat vertexb,respectively.Similar to the result of Lemma 2.3,we have

Lemma 2.4LetGbe a connected graph.Ifk ≥s ≥1,thenλ(p)(G(1)(k,s))＞λ(p)(G(1)(k+1,s-1))forp ＞1.

ProofSupposeλ(p)(G(1)(k,s))≤λ(p)(G(1)(k+1,s-1)).Letxbe a positive eigenvector with‖x‖p=1 corresponding toλ(p)(G(1)(k+1,s-1)).Letau1···ukuk+1andbv1···vs-2vs-1be two pendant paths ataandbof lengthsk+1 ands-1 inG(1)(k+1,s-1),respectively.For convenience,letu0=a,v0=b.We will prove by induction that

Fori=0,ifxuk ≤xvs-1,letG1=G(1)(k+1,s-1)-{ukuk+1}+{vs-1uk+1}.Note thatG1G(1)(k,s).By Lemma 2.2,we haveλ(p)(G(1)(k,s))=λ(p)(G1)＞λ(p)(G(1)(k+1,s-1)),which is a contradiction.Hence,xuk ＞xvs-1.

Case 1k-s ≥1.

which is a contradiction.

Case 2k=s.

Note thatxuk-s+1=xu1＞xb.LetG5=G(1)(k+1,s-1)-{ub|u ∈NG(b){a}}+{uu1|u ∈NG(b){a}}.Clearly,G5G(1)(k,s).By Lemma 2.2,we haveλ(p)(G(1)(k,s))=λ(p)(G5)＞λ(p)(G(1)(k+1,s-1)),which is a contradiction.

This completes the proof.

Supposea,b,ware three vertices ofGsuch thatdG(a)≥2,dG(b)≥2,dG(w)=2,anda～w,b～w,a≁b.LetG(2)(k,s) be the graph obtained fromGby attaching a pendant path of lengthkat vertexaand attaching a pendant path of lengthsat vertexb,respectively.

Lemma 2.5LetGbe a connected graph.Ifk-1≥s ≥1,thenλ(p)(G(2)(k,s))＞λ(p)(G(2)(k+1,s-1))forp ＞1.

which also contradicts to our assumption.

Case 2k=s+1.

This completes the proof.

Lemma 2.6LetGbe a connected graph withuv ∈E(G)anddG(u),dG(v)≥2.Supposeuandvhave no common neighbors.LetG*be the graph obtained fromGby deleting the edgeuv,identifyinguandvas a new vertexwand attaching a pendant vertex tow.Then forp ＞1

ProofLet

In the following proofs,we will frequently use the following Lemma.

Therefore,xv1=xu2,xv2=xu1.

This completes the proof.

Lemma 2.8LetGbe a graph amongG(n,c,k) obtaining the maximump-spectral radius,wherec ≥0,p ＞1.Letuandvbe two vertices ofG.Then we have

(a)ifdG(u)＞dG(v),thenxu ＞xv;

(b)ifxu ＞xv,thendG(u)≥dG(v);

(c)ifxu=xv,thendG(u)=dG(v).

Proof(a)Suppose to the contrary thatxu ≤xv.Note that there exists a shortest pathPuvbetweenuandv.LetdG(u)-dG(v)=r.Notice thatr ＞0.Then there must existw1,···,wr ∈NG(u)NG(v)andw1,···,wr/∈V(Puv).LetG1=G-{wiu | i=1,···,r}+{wiv | i=1,···,r}.Clearly,G1∈G(n,c,k).By Lemma 2.2,we haveλ(p)(G1)＞λ(p)(G),which is a contradiction.Hence (a)holds.The statement of(c)is immediately from(a).

Now,we prove(b).Otherwise,ifdG(v)-dG(u)=r ＞0,by the statement of(a),we havexv ＞xu,which is a contradiction.Hence(b)holds.

Definition 2.1LetGbe ac-cyclic graph withc ≥1 andu ∈V(G).A closer vertexvofuis a vertex adjacent tousatisfyingd(v,)=d(u,)-1.A further vertexwofuis a vertex adjacent tousatisfyingd(w,)=d(u,)+1.

Lemma 2.9LetGbe ac-cyclic graph amongG(n,c,k)obtaining the maximump-spectral radius,wherec ≥1.ThendG(v)≤2 for anyv ∈V(G)V().

Obviously,G1∈G(n,c,k).By Lemma 2.2,λ(p)(G1)＞λ(p)(G),which is a contradiction.

This completes the proof.

Lemma 2.11LetGbe ac-cyclic graph amongG(n,c,k)obtaining the maximump-spectral radius,wherec ≥1.Then there is at most one vertexusuch thatdG(u)≥max{4,c+2}.

This completes the proof.

3 Proof of Theorem 1.1

For 3≤k ≤n -1,letTkbe a tree attaining the maximump-spectral radius amongT(n,k),λ(p):=λ(p)(Tk)be itsp-spectral radius,andxbe a positive eigenvector ofλ(p).Note that the number of vertices of degree 2 isn-1-k.In the rest,we useTinstead ofTkfor convenience.

Lemma 3.1There is a unique branching vertex inT.

ProofSuppose to the contrary that there are two branching verticesuandv.Without loss of generality,letxu ≥xvandPuvbe the unique path connectinguandv.

Proof of Theorem 1.1Without loss of generality,letu0be a vertex withdT(u0)=Δ(T).By Lemma 3.1,Thas a unique branching vertexu0.Thus,the end-vertices of each segment isu0and a pendant vertex ofT,anddT(u0)=k.Therefore,Tn,kis the unique tree obtaining the maximump-spectral radius amongT(n,k)by Lemma 2.3.

This completes the proof.

4 Proof of Theorem 1.2

For 2≤k ≤n,letUkbe a unicyclic graph obtaining the maximump-spectral radius amongU(n,k),and letλ(p):=λ(p)(Uk)be itsp-spectral radius andxbe a positive eigenvector ofλ(p).In the rest,we useUinstead ofUkfor convenience.

LetClbe the unique cycle inU.Note that 2≤k ≤n,we have 3≤l ≤n-1,3≤Δ(U)≤k+1 and there is at least one pendant vertex inU.

SinceClis the base ofU,by Lemma 2.9,we know thatUis a unicyclic graph obtained fromClby attaching some pendant paths to the vertices ofCl.Letu0be a vertex such that=max{xv|v ∈V(U)}.It follows thatdU(u0)=Δ(U)≥3 by Lemma 2.8(b).Note thatu0∈V(Cl).

This completes the proof.

LetP=u0v1···vqbe a pendant path ofU.We prove our result under the following subcases.

This completes the proof.

Lemma 4.2If there are at least two branching vertices inU,then the base ofUisC3.

ProofBy Lemma 2.11,we know that all branching vertices except the maximum degree vertexu0are vertices of degree 3 inU.

Ifl=4,we claim thatUhas exactly two branching vertices.Otherwise,vis adjacent tou0onCl.Note thatdU(u0)=Δ(U),dU(v)=3.Therefore,the edgeu0vis a segment.LetU1be a unicyclic graph obtained fromUby deleting the edgeu0vand identifyingu0andvas a new vertexz,and attaching a pendant vertex toz.Obviously,U1∈U(n,k)and the length of its unique cycle is 3.By Lemma 2.6,λ(p)(U1)＞λ(p),which is a contradiction.Therefore,the neighbor ofu0onClare all vertices of degree 2.

Therefore,the base ofUisC3.

Lemma 4.3Ifn ≥k+2,thenUhas exactly one branching vertexu0.

Proof of Theorem 1.2(1) Ifn=k,thenUhas no vertex of degree 2,i.e.,any edge is a segment.Note thatUhas at least three branching vertices in this condition.Hence,by Lemma 4.2,the length of the unique cycle inUis 3.Let the unique cycle beC3=u0u1u2.By Lemma 2.11,we can assumedU(u0)=k-3 anddU(u1)=dU(u2)=3.Clearly,UΔ(k-5,1,1),(1)holds.

(2)Ifn=k+1,thenUhas exactly one vertex of degree 2,denoted byv.Note thatUhas at least two branching vertices in this condition.Hence,by Lemma 4.2,the length of the unique cycle inUis 3.Let the unique cycle beC3=u0u1u2.AssumedU(u2)≤dU(u1)≤dU(u0).We havedU(u1)=3 and 2≤dU(u2)≤3 by Lemma 2.11.Next,we provedU(u2)=2.

5 Proof of Theorem 1.3

LetBbe a bicyclic graph.It is well known that there are three types ofas follows:

A∞-graph,denoted byB(k,s),is a bicyclic graph obtained from two vertex-disjoint cyclesCkandCsby identifying verticesuofCkandvofCs.

A dumbbell graph,denoted byB(k,t,s),is a bicyclic graph obtained from two vertex-disjoint cyclesCkandCsby joining verticesuofCkandvofCswith a new pathPt+1=uu1···ut-1vof lengtht(t ≥1).

For 2≤k ≤n+1,letBkbe a bicyclic graph attaining the maximump-spectral radius amongB(n,k),and letλ(p):=λ(p)(Bk)be itsp-spectral radius andxbe a positive eigenvector ofλ(p).In the rest,we useBinstead ofBkfor convenience.

Obviously,B*=Q(2,1,2)andB**=B(3,3).Whenn=4,there is a unique bicyclic graphB*;whenn=5,there are exactly two bicyclic graphsQ(2,1,3)andB**.By computation,Q(2,1,n-2)is the unique graph attaining the maximump-spectral radius amongB(n,3)forn=4 or 5.Hence,in what follows,assumen ≥6.

Lemma 2.9 shows thatBis obtained fromby attaching some pendant paths to some vertices of.

Lemma 5.1Letu0be the vertex such thatxu0=max{xu |u ∈V(B)}.Thenu0lies on a cycle andu0is a branching vertex in the baseofB.

ProofNote thatdB(u0)=Δ(B)≥3 by Lemma 2.8.Hence,u0is a branching vertex andu0∈V()by Lemma 2.9.

Claim 5.1u0lies on a cycle.

Therefore,u0lies on a cycle,sayCk.

This completes the proof.

In what follows,letu0be the vertex such that=max{xu | u ∈V(B)}.By Lemma 2.8,we havedB(u0)=Δ(B).Without loss of generality,supposeu0∈V(Ck).By Lemma 2.11,all branching vertices inBexceptu0are vertices of degree 3.

Lemma 5.2Ifk=2,thenBB(3,n-2).

ProofNote that there is no pendant vertex inBandBis an∞-graph.Therefore,by Lemma 5.1,we haveV(Ck)∩V(Cs)={u0},dB(u0)=4.SincedB(u0)=4＞dB(u)=2 for anyu ∈V(B){u0},it follows that＞xufor anyu ∈V(B){u0}by Lemma 2.8.Next,we claim thatBcontains aC3as its induced subgraph.

This completes the proof.

Claim 5.3u0～v1.

Suppose to the contrary thatu0≁v1.We proceed by the following two cases.

Case 1Bis a dumbbell graph.

Assume thatu0∈V(Ck)andv1∈V(Cs).Takeu～u0onCkandw～v1onCs,thenu≁w.LetB1=B-{u0u,v1w}+{u0v1,uw}.Clearly,B1∈B(n,k)andB1is aθ-graph.Notice thatandBy Lemma 2.7,we haveλ(p)(B1)＞λ(p),which is a contradiction.

Case 2Bis aθ-graph.

Note thatu0,v1must be on the same cycle,sayCk.Takeu～u0andw～v1onCkin clockwise direction.LetB2=B-{uu0,wv1}+{uw,u0v1}.Obviously,B2∈B(n,k)andB2is aθ-graph.Sinceby Lemma 2.7,we haveλ(p)(B2)＞λ(p),which is a contradiction.

Therefore,u0～v1.

Claim 5.4Bis aθ-graph.

Therefore,Bis aθ-graph.

Claim 5.5Bcontains aC3as its induced subgraph.

Hence,Bcontains aC3as its induced subgraph.

Therefore,by Claims 5.3,5.4 and 5.5,we obtainBQ(2,1,n-2).

Lemma 5.4If there are a unique branching vertex and at least one pendant vertex inB,thenBis obtained by attachingk-2 pendant paths of almost equal lengths to the vertex of degree 4 inB**,i.e.,

ProofNote thatBcontains an∞-graph as its induced subgraph under these conditions,and there are at least 4 vertices of degree 2.Then 3≤k ≤n-3.Let=B(k,s).ThendB(u0)=Δ(B)=k+2≥5 and there arek-2 pendant pathsattached tou0.If there are two of those pendant paths such that their lengths differ by at least 2,then we can make their lengths to at most differ by 1 without changing the number of segments.This modification will increase thep-spectral radius ofBby Lemma 2.3.Hence the pendant paths are of almost equal lengths.Similar to the proof of Lemma 4.1,we havek=s=3.

This completes the proof.

Claim 5.7u0～v1.

Hence,u0～v1.

Without loss of generality,assumel2=1.Notice thatl1,l2,l3≥1 and at most one of them is 1,we havel1≥2 andl3≥2.

Claim 5.8BothCkandCsare of lengths 3.

Ifk ≥4 ands ≥4,letB5=B-{uv1|u ∈NB(v1){u0}}+{uu0|u ∈NB(v1){u0}}.Obviously,B5∈B(n,k) andB5contains an∞-graph as its induced subgraph.By Lemma 2.2,λ(p)(B5)＞λ(p),which is a contradiction.

Therefore,at least one ofkandsis equal to 3.Without loss of generality,let|V(Cs)|=3.Next we claim|V(Ck)|=3.

Otherwise,labelCk=u0v3···vkv1andCs=u0v1v2in clockwise direction.Letvk+1=v1.Notice thatv1,v3andvkhave no further vertex by Lemma 2.2 and Lemma 2.6.If there is a branching vertexvjfor 4≤j ≤k -1,we have|V(Ck)| ≥5.By a similar proof of Lemma 4.2,we obtain a contradiction.Hence,dB(vi)=2 for anyi=3,···,k.SincedB(v1)=3 and there is a pendant vertex inB,one ofu0andv2has a further vertex.

Proof of Theorem 1.3AssumeV(B*)={u0,v1,v2,v3}withdB*(u0)=dB*(v1)=3.

(1) Ifn=k -1 andk ≥7,it follows thatBhas no vertex of degree 2 and has at least two branching vertices.By Lemma 5.5,BcontainsB*as its induced subgraph.Hence,dB(u)=1 for anyu ∈V(B)V(B*).According to Lemma 2.2 and Lemma 2.8,dB(v1)=dB(v2)=dB(v3)=3,dB(u0)=Δ(B)=k-4.SoBH1,(1)holds.

(2) Ifn=kandk ≥5,it follows thatBhas exactly one vertex of degree 2 and has at least two branching vertices.By Lemma 5.5,BcontainsB*as its induced subgraph.AssumedB(v2)≥dB(v3).It must havedB(v2)≥3.According to Lemma 2.2 and Lemma 2.8,dB(v1)=dB(v2)=3 and 2≤dB(v3)≤3.We claim thatdB(v3)=2.

(3)Ifn=k+1 ork+2,wherek ≥4,thenBhas exactly 2 or 3 vertices of degree 2 and at least two branching vertices.By Lemma 5.5,BcontainsB*as its induced subgraph.Assume thatdB(v2)≥dB(v3).According to Lemmas 2.2 and 2.8,dB(v1)=3 and 2≤dB(v3)≤dB(v2)≤3.We claim thatdB(v3)=2.The proof is the same as(2).We omit it here.Similarly,dB(v2)=2.

(4)Ifn ≥k+3 andk ≥4,thenBhas at least 4 vertices of degree 2 and at least one pendant vertex.We consider the following two cases.

Case 1There is a unique branching vertex inB.

Case 2There are at least two branching vertices inB.

(5)Ifn ≥6 andk=3,then there are exactly the following three types of bicyclic graphs: a dumbbell graph,aθ-graph or a graph obtained from an∞-graph by attaching a new path to the branching vertex of the∞-graph.

(6)This has been proved by Lemma 5.2.

The proof is complete.