基于广义有限差分法的多孔介质墙体热湿耦合迁移模型求解
2023-10-21郭兴国罗银辉刘向伟
郭兴国,罗银辉,刘向伟*
(1.南昌大学工程建设学院,江西 南昌 330031;2.江西省超低能耗建筑重点实验室,江西 南昌 330031;3.江西省近零能耗建筑工程实验室,江西 南昌 330031)
墙体热湿耦合迁移对建筑热湿性能、室内环境及建筑能耗有着十分重要的影响。经过数十年的研究,国内外学者建立了许多墙体热湿耦合传递模型[1-6],其中应用最为广泛的是Phillip-De Vries模型[1]和Luikov模型[2]。模型能从机理上较真实地反映多孔介质墙体中的热湿迁移过程,可以就建筑材料和建筑结构在真实外界条件下长期变化的特性作出模拟,但模型中参数都是含湿量和温度的函数,这使得模型求解非常复杂,大大限制了模型的使用。因此,寻求合适的数值解法对模型进行高效稳定的求解显得尤为重要。
目前,学者们主要采用有限容积法、有限差分法和有限元法等传统数值方法求解热湿传递模型[7-9]。但这些方法都是以单元或网格为基础,编程和实际应用比较复杂和困难。为了摆脱单元或网格的束缚,使编程容易实现,涌现出了许多无网格法,其中广义有限差分法(GFDM)[10]是其中最具前景的方法之一。目前广义有限差分法已成功分析了许多问题,如抛物线和双曲方程[11]、输流直管振动响应特性问题[12]和非定常Burgers方程[13]等,这些问题的解决展现出了GFDM求解的准确性、高效性和稳定性,证明了GFDM强大的应用潜力。
本文针对一维多孔介质的热湿耦合迁移微分方程,提出一种准确、高效和稳定的无网格数值解法,采取隐式欧拉法和GFDM法分别对时间和空间进行离散,并在Matlab软件上进行编程求解。通过与解析解、有限差分法(传统解法)、有限差分法的对三角矩阵解法(TDMA)和实验结果进行对比,验证了本文提出的数值解法的稳定性和高效性,并分析了不同的区域总点数、子区域选点数以及时间步长对该方法计算精度的影响。
1 热湿耦合传递模型
1.1 控制方程
所采用的传热传质模型是基于Luikov模型[2],并作出以下假设:
1)材料是均匀的且热物理性质是恒定的。
2)流体和多孔介质之间存在局部的热力学平衡。
3)墙体的初始含水率和温度分布均匀。
故一维多孔介质墙体热湿耦合迁移控制方程[14]为
(1)
(2)
式中:T为温度,单位K;m为湿度势,单位°M;t为时间,单位s;Cp为材料的比热容,单位J·(kg·K)-1;Cm为材料的比湿,单位kg·(kg·°M)-1;Dm为湿传递系数,单位kg·(m·s·°M)-1;k材料为导热系数,单位W·(m·K)-1;ρ为物体的干密度,单位kg·m-3;ε为相变因子,单位m3·m-3;γ为吸收或解吸热,单位kJ·kg-1;δ为热梯度系数,单位°M·K-1;hlv为蒸发潜热,单位J·kg-1。根据吸湿性材料中传热和传质的热力学相似性,湿度势m被定义为含水率w的线性函数[14]:
w=Cmm
对式(1)和式(2)进行拉普拉斯变换,即
(4)
(5)
式中:
(6)
(7)
(8)
(9)
1.2 边界条件
如图1所示,x为距离内墙表面的距离,l为墙体的厚度,假设多孔建筑墙体只在水平方向进行热湿传递,垂直方向的温度和湿度势保持均匀,边界条件方程如下所示:
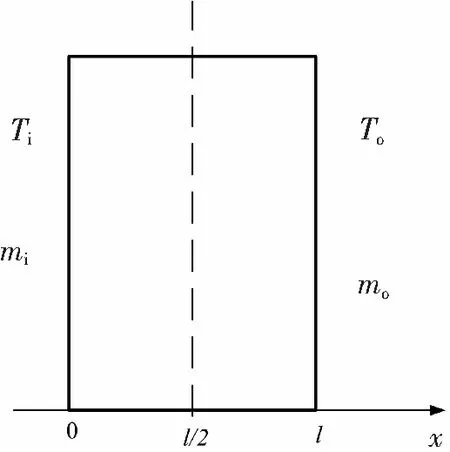
图1 墙体的一维示意图Fig.1 One-dimensional diagram of the wall
T(x,t)|x=0=Ti
(10)
T(x,t)|x=l=To
(11)
m(x,t)|x=0=mi
(12)
m(x,t)|x=l=mo
(13)
1.3 初始条件
模型的初始温度和湿度势分别为:
T(x,t)|t=0=Tb
(14)
m(x,t)|t=0=mb
(15)
2 数值求解
在求解过程中,隐式欧拉法相比显式欧拉法更加复杂,但采用隐式欧拉法可以解除时间步长的严格限制,并具有更好的稳定性和精度。所以对式(3)和式(4)的时间项采取隐式格式差分进行离散,得到式(16)和式(17):
(16)
(17)
利用广义有限差分法对热湿耦合迁移控制方程进行空间离散,对于给定的第i个节点和它附近的ns个相邻的节点构成一个区域,如图2所示,同时以给定的第i点为中心进行泰勒形式展开,定义一个新的函数B(φ):
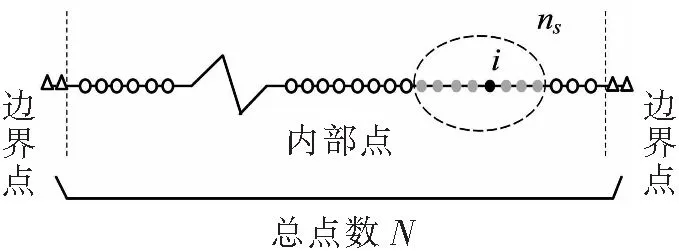
图2 选点示意图Fig.2 Schematic diagram of point selection
B(φ)=
(18)
式中:j为节点的位置索引;δij为沿着坐标轴方向的距离;w(δij)代表的是区域内的j点对i点的权重函数,即
w(δij)=
(19)
其中dmi为第i个节点与所选区域最远点的距离。对于二维或三维的问题则被认为是区域的半径。然后对泛函数求极小值可得
A·Dφ=b
(20)
(21)
(22)
(23)
矩阵A是对称矩阵,Aφ的具体向量表达式取决于区域内的点数。同时我们可以将矩阵A重新写成以下形式:
b=BQ
(24)
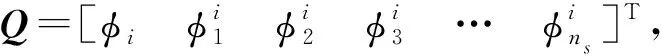
(25)
由式(25)可以看出第i个节点可以用ns+1个点的不同加权系数的线性组合来表示,其中矩阵D取决于权重函数,节点坐标以及中心节点所选择的周围区域节点数。根据前人研究[15-16],选点数ns取值大于10能获得更好的稳定性,故本文相邻节点选点数均取10个以上。偏微分项可以进一步详细表示为
(26)
(27)
3 验证与分析
3.1 参数选择
模型的物性参数按照文献[5]中进行取值,其中Cm为0.01 kg·(kg·°M)-1,Cp为2.5 kJ·(kg ·K)-1;Dm为2.2×10-8kg·(m ·s·°M)-1;k为0.65 W·(m ·K)-1;ρ为370 kg·m-3;ε为0.3 m3·m-3;γ为0 kJ·kg-1;δ为2 °M·K-1;hlv为2.5 MJ·kg-1;l为0.024 m;Tb为283 K;Ti为333 K;To为383 K;mb为86 °M;mi为45 °M;mo为4 °M。
在计算过程中,计算区域总点数N为301,子区域选点数ns=13,时间步长dt=1 s。将方程离散后并结合对应的边界条件和初始条件后进行迭代求解。
3.2 模拟结果的分析和讨论
3.2.1 与其他数值结果对比
图3为墙体中间点温度和湿度势随时间变化的曲线,从图中可以看出利用GFDM方法计算出来的结果与解析解、有限差分法及TDMA解法结果高度吻合。墙体中间位置(x=0.012 m)温度在800 s附近就开始趋于稳定,并后续一直保持在356.5 K左右。而在4 000 s的计算过程中湿度势的大小先是维持缓慢上升,后趋于稳定,再保持下降的趋势。而将计算时间延至24 h后,温度大小基本维持不变,但湿度势却一直在降低并最后稳定在24.5 °M左右。表1为3种数值方法和解析解的平均误差与效率对比,可以看出GFDM与有限差分精度的差距甚微,但其运行效率却提升了16.6%。而TDMA算法虽然计算时间很快,但其误差相对其他2种数值方法较大,且在求解过程中TDMA算法稳定性差,极易受到时间和空间步长的影响。

表1 平均误差和计算时间Tab.1 Average error and calculation time

t/s(a) 温度
3.2.2 与实验结果对比
将利用GFDM的数值方法计算的结果与文献[17]中的实验结果进行对比,参数设置参考文献[17]。建筑墙体的温度计算结果分布图如图4(a)所示,实验结果和数值结果的平均相对误差小于10%。v代表水蒸气含量,单位为kg·m-3,从图4(b)墙体水蒸气含量分布图可以看出,该数值解法与实验结果的平均相对误差小于8.5%。故从图4可以看出,该数值方法计算的结果与实验结果的温度和水蒸气含量的误差均在合理范围内,误差较大的地方可能是实验过程的中存在不可控因素以及数值解对模型进行了某些简化导致的。

x/m(a) 温度
3.3 步长和取点数对GFDM结果的影响
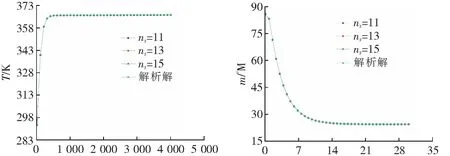
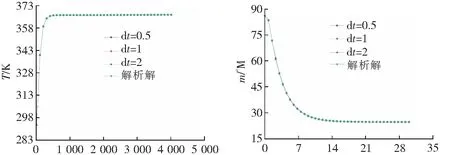
为研究不同总区域点数,不同子区域选点数和时间步长对该数值方法的影响,再用3.1节中的参数进行数值模拟分析。如图5所示,随着总区域点数N的增大,温度和湿度势的数值结果几乎没有发生改变,表明在一定范围内总点数对数值结果的精度几乎没有影响。图6则表明随着子区域选点数ns的增大,温度和湿度势的数值结果越精确,但这种精确度的提升是非常小的。从图7可以看出,不同时间步长计算出来的数值结果具有良好的一致性。综合图5~图7结果可以得出:该数值解法几乎不受总区域点数,子区域选点数和时间步长的影响,从而证明了该数值方法拥有良好的稳定性。且从图5~图7中也可以看到,由于材料的热扩散系数大于湿扩散系数,温度比湿度势能够更快地进入稳定的状态。
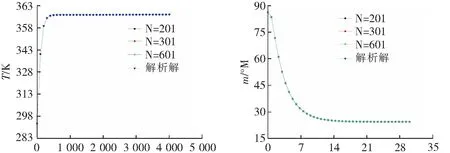
t/s(a) 温度t/h(b) 湿度势
t/s(a) 温度 t/h(b) 湿度势
t/s(a) 温度 t/h(b) 湿度势
4 结论
本文运用新型无网格法对多孔介质墙体的热湿耦合迁移控制方程进行求解,在时间上采用不受时间限制的隐式欧拉法离散,空间上采用摆脱了网格生成和数值求积的GFDM法离散,运用Matlab软件进行编程求解,并将模拟的数值结果与解析解、其他数值解及实验结果做了对比和分析。结果表明该数值结果与解析解、其他数值解和实验的结果非常吻合,从而验证了该数值方法的准确性和高效性。同时,文中还给出了该数值方法在不同的总区域点数、子区域选点数以及时间步长的解,验证了该方法的稳定性。
