不规则物体点云切片中的多轮廓分割算法

张瑾，徐文，周宇乔，刘凯*

不规则物体点云切片中的多轮廓分割算法

张瑾1，徐文1，周宇乔2，刘凯1*

（1.四川大学 电气工程学院，成都 610065； 2.绿色化学与技术教育部重点实验室（四川大学），成都 610064）（ ∗ 通信作者电子邮箱kailiu@scu.edu.cn）

使用切片法进行不规则物体点云体积测量时，现有的多边形拆分再重组（PSR）算法难以正确拆分较近的轮廓，进而导致计算精度较低。针对这一问题，提出一种多轮廓分割算法——改进最近点搜索（INPS）算法。首先，通过局部点的单次使用原则分割多轮廓；其次，使用多边形内点判定（PIP）算法判断轮廓的包含关系，以确认轮廓面积的正负；最后，采用切片面积乘以厚度并累加的方式获取不规则物体点云的体积。实验结果表明，在两个公开点云数据集和一个化学电子密度等值面点云数据集上，所提算法都能实现高正确率的边界分割，具有一定的普适性；且该算法体积测量的平均相对误差为0.043 6%，低于PSR算法的0.062 7%，可见所提算法实现了高正确率的边界分割。

点云体积测量；点云切片；多轮廓分割；多边形内点判定算法；最近点搜索法

0 引言

体积是三维空间中物体的重要属性参数［1］，体积计算是空间中对象形态分析的基本内容［2］，涉及规则几何体和不规则几何体。其中，不规则几何体的体积测量，因为它的形态各异，无法归纳普适的计算方法，仍是普遍面临且亟待解决的现实难题［3］。三维激光扫描的方式可以快速获取包含物体表面结构信息的点云数据，由此得到对象的三维封闭曲面模型或者多层二维轮廓边界，这两种方法均可计算不规则物体体积，即逆向建模法和切片法技术路线。前者体积计算准确可靠，但需要经过扫描阶段、点云阶段和曲面拟合阶段才能生成目标模型［4］，而且需要进行拓扑检查和孔洞填充等操作［5］，计算过程耗费资源和时间；后者将一个三维曲面问题简化成了多个二维曲线问题，降低了空间复杂度，以牺牲小部分精度的代价大幅减少了计算时间。因此，切片法因具有直观和易于编程实现的优势，被广泛地应用于工程项目中，如不规则树冠体积测量［6］、商品包装体积测量［7］、油罐和洞库容量计量［8］和船舶排水量计量［9］等诸多领域。此外，在计算化学理论研究领域，针对分子范德瓦尔表面上静电势的研究可以用于预测反应位点，预测分子性质，解释分子间弱相互作用；而分子范德瓦尔表面（后文称为分子电子密度等值面）的体积是一个重要参数，本文中使用Multiwfn［10］得到分子电子密度格点数据和静电势格点数据，经过处理得到相应点云［10-11］。

切片法测量体积的流程可以概括为获取点云数据、点云数据切片、切片上点云投影、多轮廓分割及包含关系判断、点云片面积计算和点云体积计算这6个步骤。其中，切片面积计算需要正确排序截面上无规则的点，生成轮廓边界，是得到正确体积值的关键。现有的边界排序算法中，极坐标排序法［9］不适用于极端凹多边形，点云轮廓提取法易扩大轮廓体积［12］，依据最小夹角原则的轮廓排序法［13］和凹包点内插法［14］在面对复杂轮廓情况时仍会出错，双向最近点搜索法［3，15］表现较好，但仍然和前两者一样局限于如墩台、储油罐和船舶等单一轮廓边界排序。使用先分类后排序思想时，-means聚类［16］、谱聚类［17］等需要事先已知分类个数的算法不适用于此类情况。使用数字图像方法可以分割多个轮廓，但它们对格栅大小的要求严格，且两次矢栅转换会引入新的误差［18］。多边形拆分再重组（Polygon Splitting and Recombination， PSR）算法［19］虽然可以区分多个轮廓，但当切片上存在较多轮廓随机分布时，基于统计学方法对异常边拆分的方式的可靠性会较低。

针对以上不足，本文提出改进最近点搜索（Improved Nearest Point Search， INPS）算法。首先，通过局部点的单次使用原则分割多轮廓；其次，使用多边形内点判定（Point Inclusion in Polygon， PIP）算法［20］判断轮廓的包含关系，确认轮廓面积的正负；最后，采用切片乘以厚度并累加的方式得到点云的体积，即不规则物体体积。

1 基本原理

本文算法最初针对分子电子密度等值面点云，该类点云的形状轮廓相对简单，但在实际的分层中，截面上会出现数量偏多且随机分布的轮廓边界。本文选择手性双氮氧金属配合物催化剂与底物结合模型电子密度等值面点云（简称Cat6点云）作为实验对象，它的表面变化大，分层情况复杂，如图1所示。

图1　实验点云Cat6

图2　分子电势点云生成流程

点云数据是计算的基础，它的获取途径通常是三维激光扫描，本文数据和激光扫描得到的数据的分层方式不同。

对于激光扫描数据，它的分层数为：

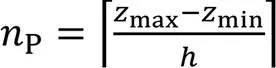
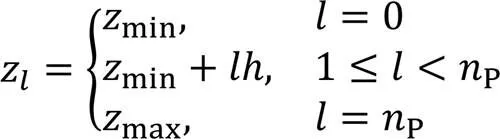
对于分子电子密度等值面点云，它的分层数为：

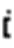
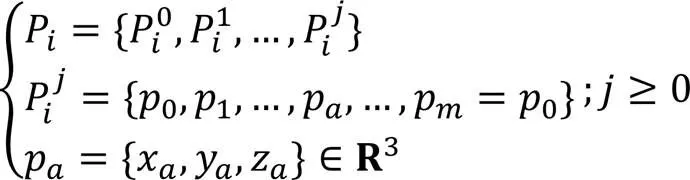
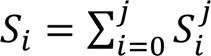
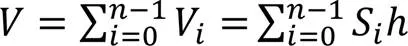
1.1　点云数据切片

MC算法的基本思想如下：遍历格点数据中所有的体素（由8个点构成的长方体），根据它的顶点值与等值面阈值的关系，将它归类到15种关系之一［21］，通过插入三角形重建物体的表面。取图2（b）中分子等值面点云顶部两层，通过观察电子密度格点点云中等值面内部的点与重建后等值面上的点之间的位置关系，归纳针对此类点云的一种切片上投影点的预处理方法，可以有效去除非轮廓上的点，流程如图3所示。

图3（a）中红色点表示格点点云在曲面内的点，蓝色点表示重建后的电子密度等值面点云，图3（b）为图3（a）中黑框所示的顶部两层的点云，重建后的蓝色点与红色点重合或者在红色点外部。两层红点之间散落着一些蓝色点，这是通过MC算法插值得到的三角形的顶点。图3（c）是连接这些三角形后的示意图。图3（d）是俯视视角示意图，其中绿色线段是观察子图3（c）画出的轮廓线。可以看出，轮廓线上的点均没有落在棋盘格点上（沿轴方向投影，格点文件某一层的点呈现类似于围棋棋盘格点的分布），图3（e）中列出的几种边界处体素的情况可用于解释。其中，绿色点表示格点点云在等值面外的点，根据它们的分布，在体素内插入不同数量和位置的三角形，并将三角形沿轴方向投影，落在棋盘格点上的点均处于体素上下两层间的棱上，而构成轮廓线的点正是那些在体素上下两层面上的点。

图3　MC算法处理后的轮廓线示意图

因此，针对由MC算法得到的点云，按照式（4）分层后，再将落在棋盘格点上的点剔除，从而得到高质量的轮廓线，从上述点云中选取其中3层，展示轮廓分布情况，如图4所示。

图4　具有代表性的两层切片点云投影

1.2　多轮廓分割

最近点搜索法和双向最近搜索法的搜索策略是连接平面上所有的点，因此这两种方法都无法区分多个轮廓。本文提出的INPS是基于局部点单次使用原则区分不同轮廓：对于一个理想的轮廓点集，每一个点只需和距离自身最近的两个点连接，得到一个闭合的轮廓线。因此，当一个点附近的所有点均已被使用（即进行过连接），则判断已经完成一次轮廓连接，并从下一个未使用过的点开始连线。具体步骤如下：

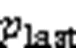
4）判断是否完成所有轮廓搜索。若还有未使用点，重复步骤1），否则轮廓搜索结束。

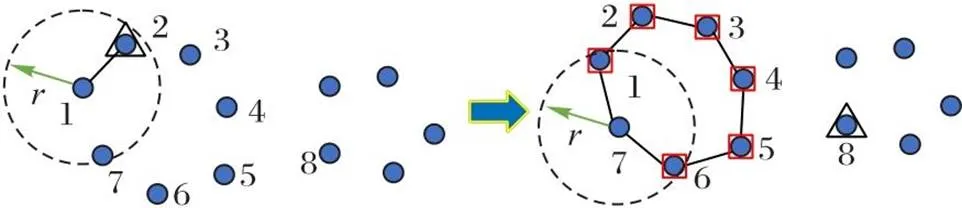
图5　INPS算法进行点集分割

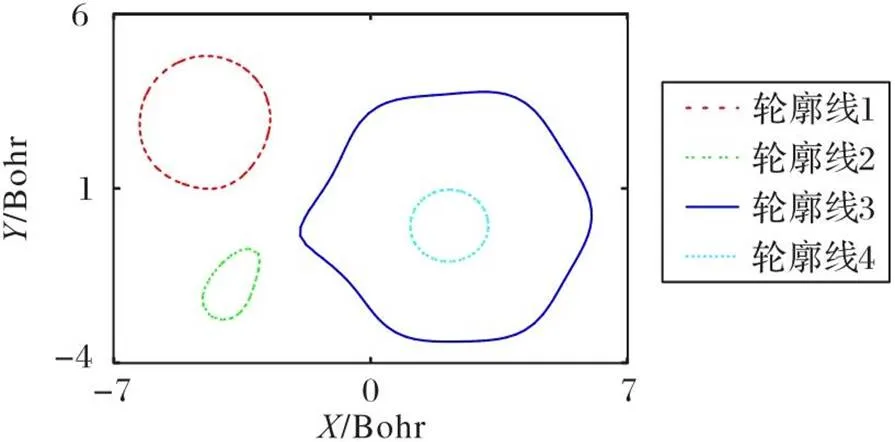
图6　经INPS算法处理后的轮廓线

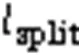
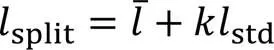
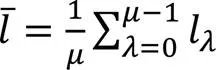
1.3　截面面积计算

精确的截面面积计算决定了不规则物体体积计算的准确度，而轮廓之间包含关系的正确判断，是截面面积精确计算的关键。点云切片中的轮廓只应存在包含和相离两种位置关系，判断方法如图7所示，常见的分布情况如图8所示。INPS算法的判断思路是：首先，使用高斯面积公式［1］计算各个轮廓的面积；其次，使用PIP算法判断轮廓间的位置状态，判断每个轮廓和除自己以外的轮廓之间的包含关系，若该轮廓被其他轮廓包含，则记录该轮廓被包含数加1；最后通过式（12）判断轮廓面积正负。

其中表示轮廓被包含的次数。

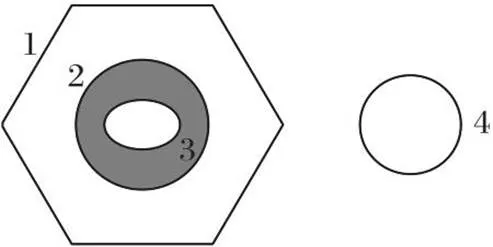
图8　多轮廓位置关系

在图7中，使用INPS算法将点集分为3个轮廓点集，分别用圆形、三角形和正方形表示。判断三角形点集和正方形点集是否被圆形点集包含，只需要从每个点集中任选一个点，找到圆形轮廓线中与该点相交的线段，确定线段的方向（例如从轴方向小值指向大值），然后计算点与线段法向量的乘积。若所有值的乘积为负数，则被包含；反之则不包含。图8中轮廓2只被轮廓1包含，因此面积为负数，而轮廓3被包含2次，面积仍为正。

2 实验与结果分析

逆向建模法计算得到的体积准确可靠，可以作为本文点云体积的真值，作为改进算法的检验依据。因此，本文使用Geomagic Wrap 2017软件计算点云体积真值和截面面积真值。实验基于Matlab语言实现了INPS算法和多边形拆分再重组（PSR）算法［19］，并对比分析了使用场景和计算精度。

2.1　分子电子密度点云

针对分子电子密度等值面点云，对比INPS算法和PSR算法［19］的结果。表1为Cat6点云数据信息，使用两种算法时，PSR算法和INPS算法的轮廓分割系数分别为2.5、3.0。使用PSR算法时，6个位置数据下的标准差与分割阈值见表2。选取Cat6点云在3个方向上具有代表性的3个位置进行展示，沿3个方向投影的平面均命名为，结果如图9～11所示。通过观察发现沿轴切片时，轮廓的情况最复杂，数量多且随机分布，因此重点分析该方向。针对Cat6点云的6个切片位置，使用Geomagic Wrap计算得到的面积作为真值，误差分析结果见表3。

表1　Cat6点云数据信息

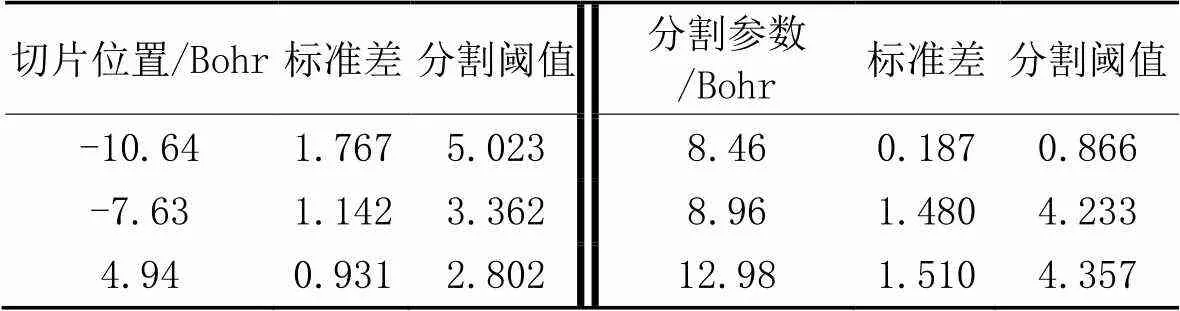
表2　PSR算法中的标准差与分割阈值

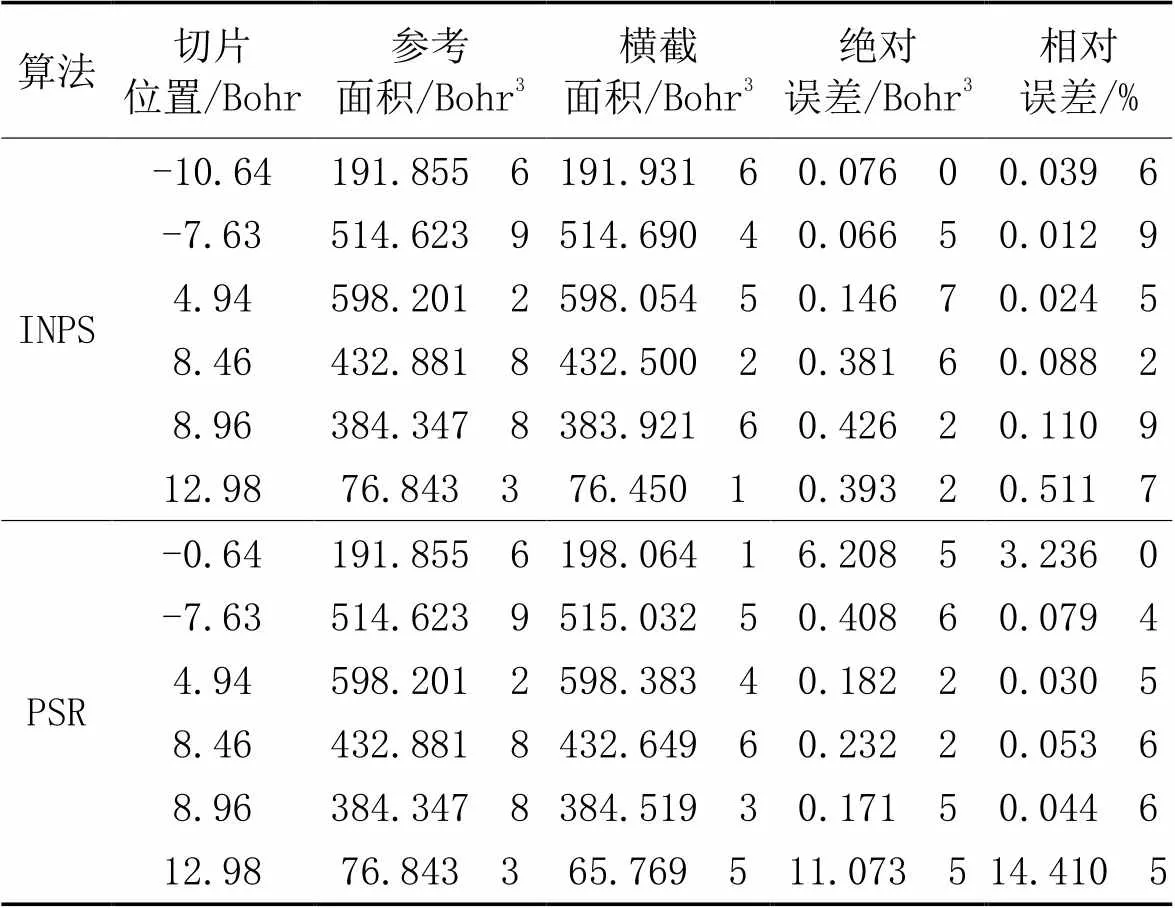
表3　Cat6点云不同切片位置处截面面积计算结果对比（Z轴）

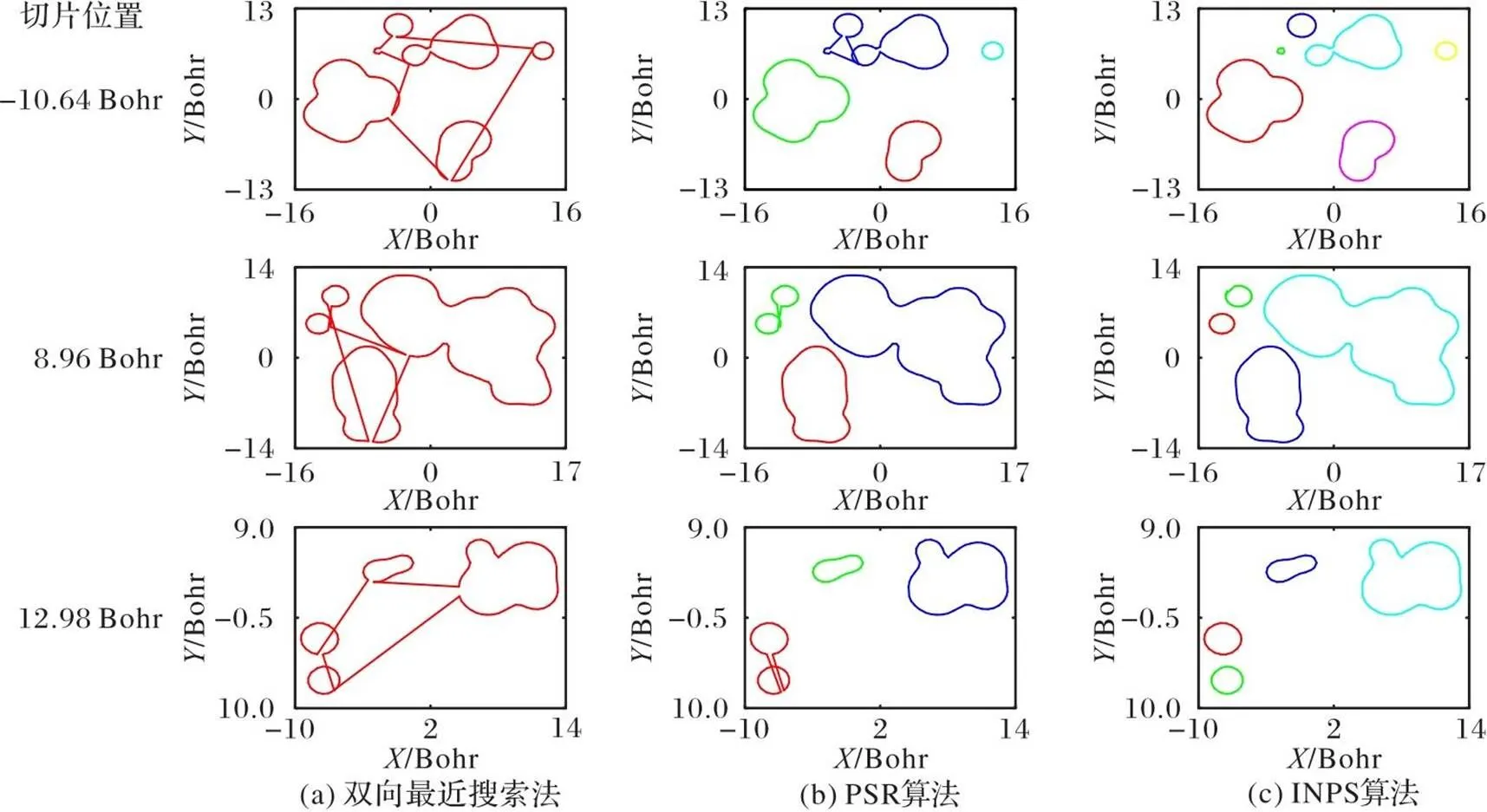
图9　Cat6点云在不同切片位置（Z轴）的轮廓分割结果对比

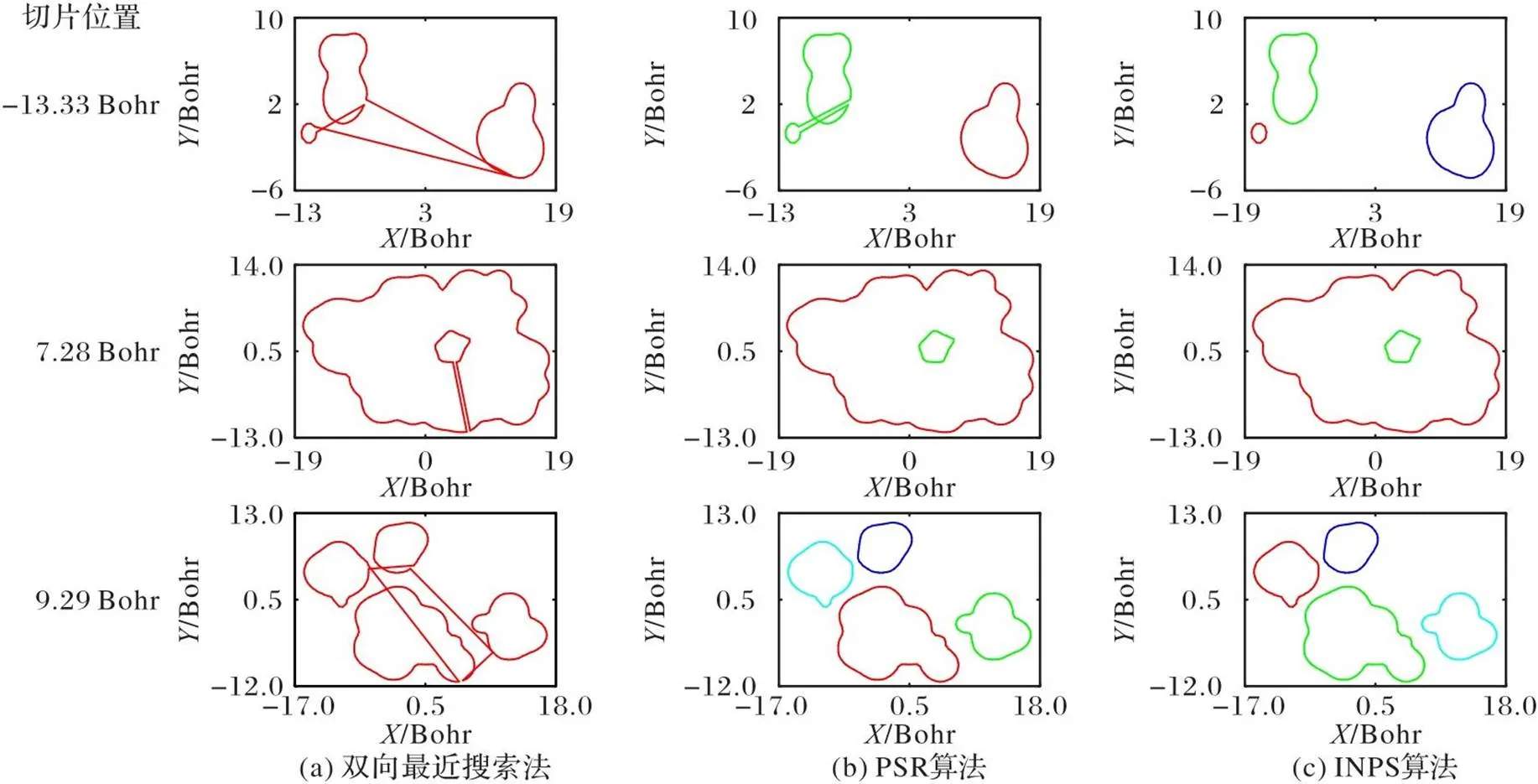
图10　Cat6点云在不同切片位置（Y轴）的轮廓分割结果对比

图11　Cat6点云不同切片位置（X轴）的轮廓分割结果对比

2.2　公开点云数据集

为验证算法的有效性和鲁棒性，使用三维激光扫描公开数据集（由斯坦福大学计算机图形学实验室公布）中Stanford Bunny和Happy Buddha（如图12所示）进行实验。

图12　实物和三维曲面模型

由于原始点云密度较低，造成切片质量差，因此对原始点云上采样。先使用移动最小二乘法（Moving Least Squares， MLS）对三维点云进行平滑拟合，然后重采样。与分子点云相比，Stanford Bunny和Happy Buddha这两组数据单一轮廓的边界形状更复杂，但切片上的轮廓数较少。

两组点云的数据信息、分层间隔和轮廓分割系数取值如表4所示，处理后的结果如图13～14所示（其中PSR算法的效果图可参考文献［19］），3个切片位置处面积的相对误差结果如表5所示。

图13　Stanford Bunny点云在不同切片位置（Z轴）的轮廓分割结果对比

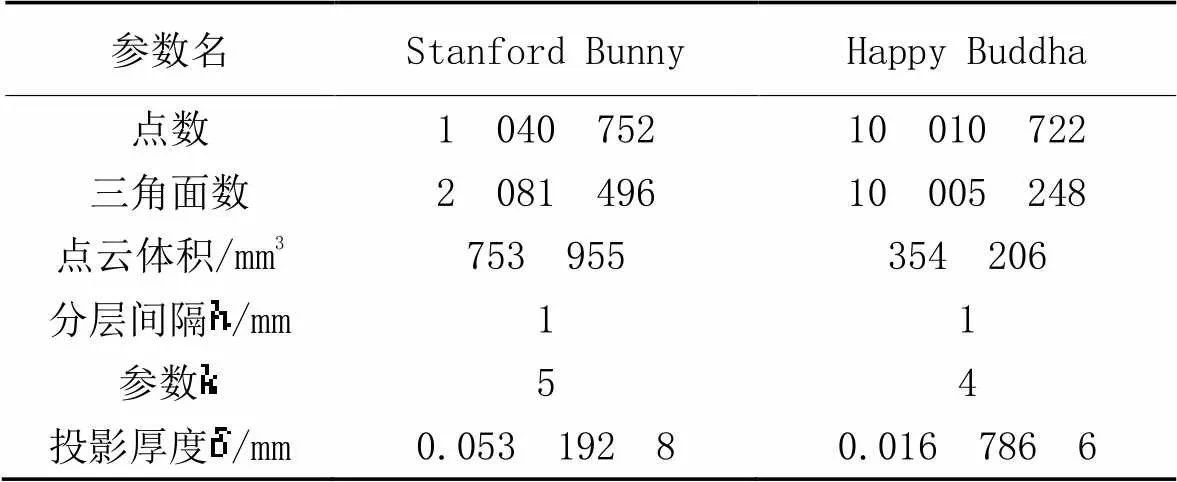
表4　两组点云数据处理中的参数

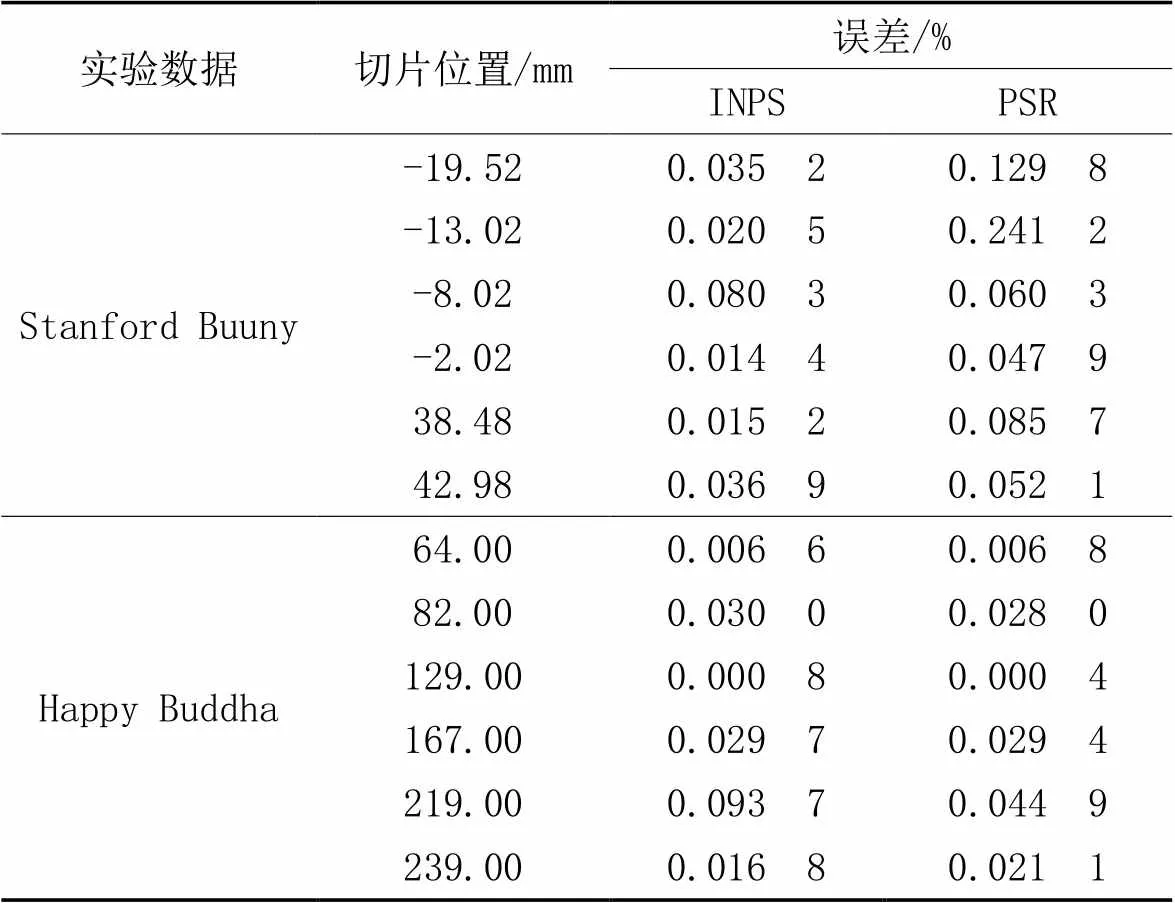
表5　PSR和INPS算法对Stanford Bunny 和Happy Buddha点云中6个截面的面积误差对比

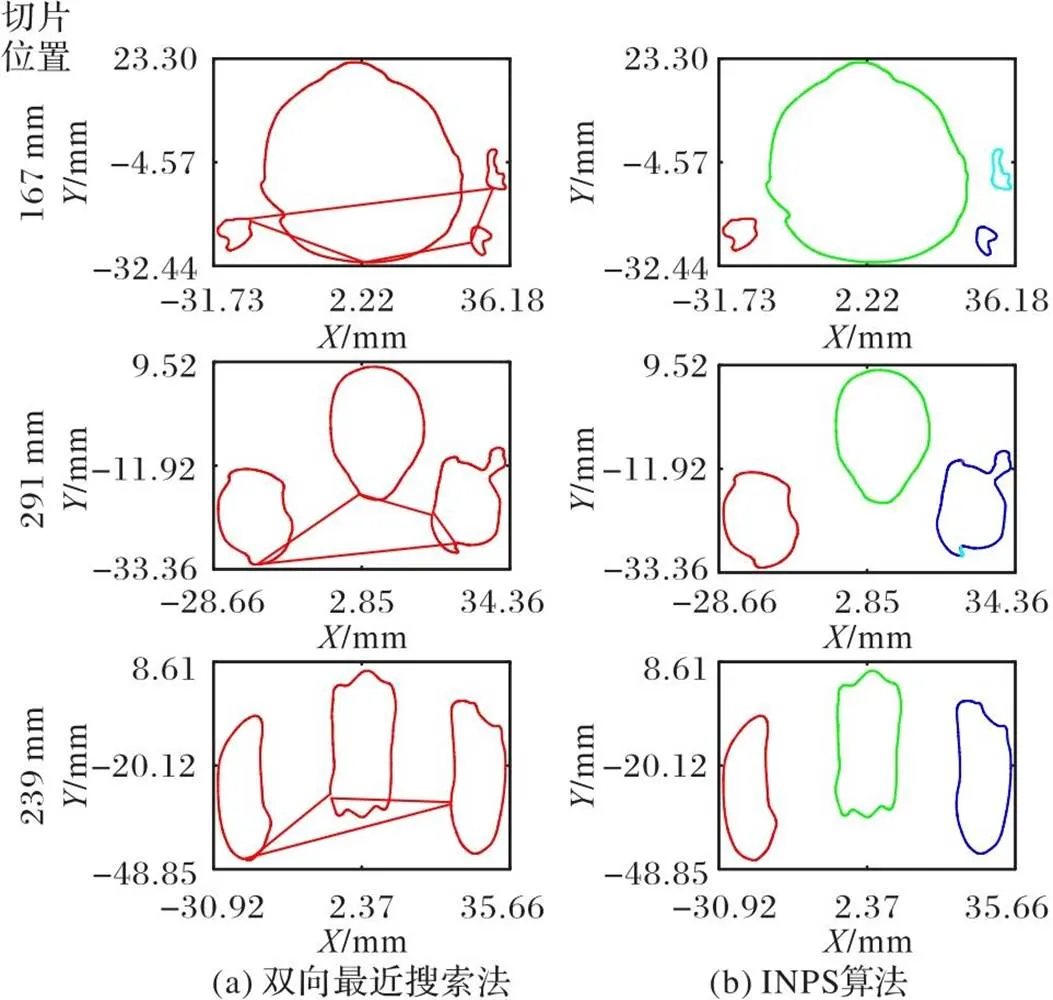
图14　Happy Buddha点云在不同切片位置（Z轴）的轮廓分割结果对比

2.3　切片多轮廓分割

根据上述实验结果，可以得出以下结论。

1）适用性。无论是针对MC算法处理后的点云，还是针对激光扫描得到的点云，INPS算法均表现了良好的轮廓分割效果，截面面积的误差也大致相同。从图9（a）可知，在针对分子电势点云时，与PSR算法相比，INPS算法的误连情况更少。在公开数据集上，INPS算法的效果和PSR算法的效果相当。

2）鲁棒性。在图9中，相较于PSR算法，INPS算法更加稳定。如图9（b）所示，PSR算法都出现了不同程度的误连，这是因为在这3幅图中，轮廓数量多，轮廓之间误连的线段也相应增多，计算得到的标准差偏大，导致一些距离较近的轮廓之间的误连线段难以被剔除，此时对式（9）中系数的选择条件较为苛刻。INPS算法的优势是，在轮廓中一点的搜索范围内，只要距离仍在该轮廓中一点的距离小于到其他轮廓任意点的距离，就不会出现误连，即使是在截面投影点质量较差的情况，也几乎不存在误连的情况，如图13～14所示。同时，INPS算法对于一个轮廓搜索完成的判定条件，使得对于系数的选择也更宽松。

2.4　点云体积计算

1）准确性。

PSR和INPS算法针对3组点云的误差都在0.1%内，并且本文算法的误差均低于PSR算法，其中，INPS算法的平均相对误差为0.043 6%，低于PSR算法的0.062 7%。如在图9中，PSR算法针对个别距离较近的轮廓没有纠正误连线段，导致该截面处轮廓的面积计算偏大。从表6可知，针对Cat6点云体积计算，INPS算法得到的体积小于PSR算法得到的体积，这也和实际情况符合。

2）高效性。

从算法的流程分析，由于PSR算法是基于双向最近点搜索法的改进算法，在最开始需要使用双向最近点搜索法排序截面中所有的点，而INPS算法在同样的排序过程中已经将点分类。这是因为INPS算法在对点排序的同时，根据伴随该点排序得到的数据也对点分类；而PSR算法更关注根据统计学数据拆分长度异常边，然后重组。因此，INPS算法在复杂度上低于PSR算法，并且实验结果也验证了INPS算法正确率略高于PSR算法。

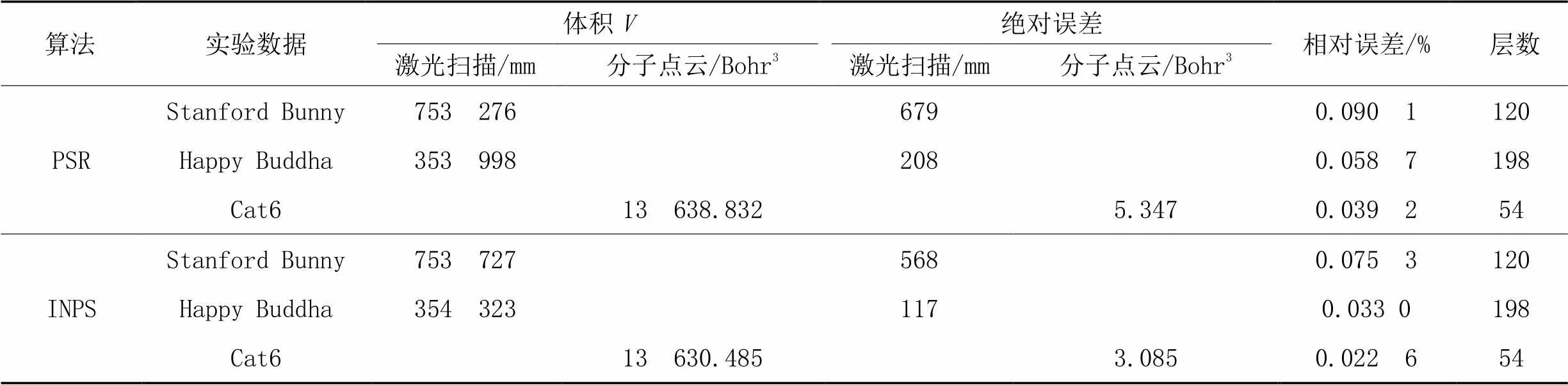
表6　PSR和INPS算法对3组数据体积测量结果的对比

2.5　误差分析

1）轮廓线不正确。针对公开点云数据集，使用投影的方法得到轮廓点时，难免出现局部点密度过大或过小的情况，导致无法反映真实的轮廓线，引入误差；而使用MC算法处理的点云，由于它的数据特征，与投影的方法相比，可以很大程度避免此类误差。

2）自相交。一个正确的轮廓线不存在其中某两条线段交叉的情况，但在点分布不规则的局部，可能会出现轮廓线相交的情况［25］。

3）使用截面面积乘以厚度模拟不规则物体在该处体积本身就存在一定的误差，并且该误差具有不确定性，可能会随机地互补，并且沿着切片的累加积累。

3 结语

本文提出了一种改进的基于最近点搜索法的多轮廓分割算法，并与多边形拆分再重组算法进行实验对比。实验结果表明，本文算法针对特定数据和公开数据集均能出色地完成多轮廓的分割，具有普适性和良好的抗干扰性；并且当存在多个轮廓随机分布时，本文算法的分割效果优于多边形拆分再重组算法。因为此时根据统计学分割异常边的可靠性较低，而本文算法的判断方式（局部点单次使用原则）更加贴合人为分割轮廓时的思维方式，故抗干扰能力更强。相较于多边形拆分再重组法，采用本文算法计算体积的正确率略高（针对3组数据的相对误差分别是0.075 3%、0.033 0%和0.022 6%），且具有更强的鲁棒性和更小的算法复杂度。但是本文算法仍存在不足，针对公开数据集，没有可靠的投影方案，若使用点云密度相关的投影厚度，则无法自适应地选取合适的投影厚度。在后续工作中，针对不同密度的点云，为了得到更高质量的轮廓点，我们将研究如何实现普适性更强的自适应截面点投影算法。

[1] 郭仁忠. 空间分析［M］. 2版. 北京：高等教育出版社， 2001： 143-145.（GUO R Z. Spatial Analysis［M］. 2nd ed. Beijing： Higher Education Press， 2001： 143-145.）

[2] ANDERSEN H E. Estimation of critical forest structure metrics through the spatial analysis of airborne laser scanner data［D］. Seattle， WA： University of Washington， 2003： 197-202.

[3] 刘明学，崔进业. 基于点云三维坐标数据计算复杂物体体积［J］. 测绘地理信息， 2018， 43（3）： 96-98.（LI M X， CUI J Y. Calculate volume of complex objects based on 3D coordinates of points cloud data［J］. Journal of Geomatics， 2018， 43（3）： 96-98.）

[4] 魏言标，郑磊，薛少兵，等. 基于三坐标测量和3D扫描的凸轮逆向建模设计［J］. 机械设计， 2021， 38（9）： 71-74.（WEI Y B， ZHENG L， XUE S B， et al. Reverse modeling design of the cam based on three-coordinate measurement and 3D scanning［J］. Journal of Machine Design， 2021， 38（9）： 71-74.）

[5] 王鑫龙，孙文磊，张建杰，等. 基于点云数据的逆向工程技术研究综述［J］. 制造技术与机床， 2018（2）： 49-53.（WANG X L， SUN W L， ZHANG J J， et al. Review on reverse engineering research based on point cloud data［J］. Manufacturing Technology and Machine Tool， 2018（2）： 49-53.）

[6] 董亚涵，李永强，李鹏鹏，等. 基于改进凸包算法的树冠轮廓点提取与体积计算［J］. 测绘工程， 2018， 27（8）： 66-71.（DONG Y H， LI Y Q， LI P P， et al. Tree crown outline points extracting and volume calculation based on improved convex hull algorithm［J］. Engineering of Surveying and Mapping， 2018， 27（8）： 66-71.）

[7] 陈琛，李宝顺，包亚萍. 基于光栅投影和点云体积计算的过度包装检测系统［J］. 计算机测量与控制， 2014， 22（12）： 3919-3922.（CHEN C， LI B S， BAO Y P. Excessive packaging detection system based on point set volume calculation method and grating projection［J］. Computer Measurement and Control， 2014， 22（12）： 3919-3922.）

[8] 吕小宁，刘晓丽，段云岭，等. 地下能源储库群容积激光测量方法及现场实验［J］. 中国激光， 2016， 43（10）： No.1004002.（LYU X N， LIU X L， DUAN Y L， et al. Laser measurement method and in-situ experiment of underground energy storage caverns volume［J］. Chinese Journal of Lasers， 2016， 43（10）： No.1004002.）

[9] 张吉星，程效军，程小龙. 三维激光扫描技术在船舶排水量计量中的应用［J］. 中国激光， 2016， 43（12）： No.1204003.（ZHANG J X， CHENG X J， CHENG X L. Application of three-dimensional laser scanning technology in measurement of ship displacement［J］. Chinese Journal of Lasers， 2016， 43（12）： No.1204003.）

[10] LU T， CHEN F W. Multiwfn： a multifunctional wavefunction analyzer［J］. Journal of Computational Chemistry， 2012， 33（5）： 580-592.

[11] LU T， CHEN F. Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm［J］. Journal of Molecular Graphics and Modelling， 2012， 38： 314-323.

[12] 连强强，顾敏. 基于α-shape的三维激光点云计算树冠体积的研究［J］. 青海大学学报， 2020， 38（5）： 74-79.（LIAN Q Q， GU M. Research on the calculation of tree crown volume by 3D laser point cloud based on α-shape［J］. Journal of Qinghai University， 2020， 38（5）： 74-79.）

[13] 付敬帅，李斌. 基于点云截面数据点的多轮廓排序算法［J］. 河南科学， 2019， 37（6）： 933-937.（FU J S， LI B. Multi-contour sorting algorithm based on point cloud cross-section data points［J］. Henan Science， 2019， 37（6）： 933-937.）

[14] 程效军，熊鑫鑫，杨泽鑫，等. 基于地面激光雷达的洞库容量计量［J］. 激光与光电子学进展， 2019， 56（23）： No.231201.（CHENG X J， XIONG X X， YANG Z X， et al. Cavern capacity calculation using terrestrial lidar［J］. Laser and Optoelectronics Progress， 2019， 56（23）： No.231201.）

[15] 钱锦锋，陈志杨，张三元，等. 点云数据压缩中的边界特征检测［J］. 中国图象图形学报， 2005， 10（2）： 164-169.（QIAN J F， CHEN Z Y， ZHANG S Y， et al. The detection of boundary point of point cloud compression［J］. Journal of Image and Graphics， 2005， 10（2）： 164-l69.）

[16] JAIN A K. Data clustering： 50 years beyond K-means［J］. Pattern Recognition Letters， 2010， 31（8）： 65l-666.

[17] NG A Y， JORDAN M I， WEISS Y. On spectral clustering analysis and an algorithm［C］// Proceedings of the 14th International Conference on Neural Information Processing Systems： Natural and Synthetic. Cambridge： MIT Press， 2001 ：849-856.

[18] 程效军，方芳. 基于形态学的散乱点云轮廓特征线提取［J］. 同济大学学报（自然科学版）， 2014， 42（11）： 1738-1743.（CHENG X J， FANG F. Morphology-based scattered point cloud contour extraction［J］. Journal of Tongji University （Natural Science）， 2014， 42（11）： 1738-1743.）

[19] 刘金锦，李浩军. 基于点云切片改进法的不规则物体体积测量［J］. 光学学报， 2021， 41（23）： No.2312003.（LIU J J， LI H J. Volume measurement of irregular objects based on improved point cloud slicing method［J］. Acta Optica Sinica， 2021， 41（23）： No.2312003.）

[20] HAINES E. Point in polygon strategies［M］// HECKBERT P S. Graphics Gems IV. San Diego， CA： Academic Press， 1994： 24-46.

[21] LORENSEN W E， CLINE H E. Marching cubes： a high resolution 3D surface construction algorithm［J］. ACM SIGGRAPH Computer Graphics， 1987， 21（4）：163-169.

[22] LIU K， RAN X， GONG J， et al. Extending epipolar geometry for real-time structured light illumination Ⅱ： lossless accuracy［J］. Optics Letters， 2021， 46（4）： 837-840.

[23] JIA M， YANG X， LIU K. Automatically detecting rigidly and nonrigidly deformed facial landmarks from coarseness to fineness［J］. Journal of Electronic Imaging， 2019， 28（6）： No.063009.

[24] ZHANG G， XU B， LAU D L， et al. Correcting projector lens distortion in real time with a scale-offset model for structured light illumination［J］. Optics Express， 2022， 30（14）： 24507-24522.

[25] 柯映林，王青. 反求工程中的点云切片算法研究［J］. 计算机辅助设计与图形学学报， 2005， 17（8）： 1798-1802.（KE Y L， WANG Q. Research on point cloud slicing technique in reverse engineering［J］. Journal of Computer-Aided Design and Computer Graphics， 2005， 17（8）： 1798-1802.）

Multi-contour segmentation algorithm for point cloud slices of irregular objects

ZHANG Jin1， XU Wen1， ZHOU Yuqiao2， LIU Kai1*

（1，，610065，；2，（），610064，）

When using the slicing method to measure the point cloud volumes of irregular objects， the existing Polygon Splitting and Recombination （PSR） algorithm cannot split the nearer contours correctly， resulting in low calculation precision. Aiming at this problem， a multi-contour segmentation algorithm — Improved Nearest Point Search （INPS） algorithm was proposed. Firstly， the segmentation of multiple contours was performed through the single-use principle of local points. Then， Point Inclusion in Polygon （PIP） algorithm was adopted to judge the inclusion relationship of contours， thereby determining positive or negative property of the contour area. Finally， the slice area was multiplied by the thickness and the results were accumulated to obtain the volume of irregular object point cloud. Experimental results show that on two public point cloud datasets and one point cloud dataset of chemical electron density isosurface， the proposed algorithm can achieve high-accuracy boundary segmentation and has certain universality. The average relative error of volume measurement of the proposed algorithm is 0.043 6%， which is lower than 0.062 7% of PSR algorithm， verifying that the proposed algorithm achieves high accuracy boundary segmentation.

volume measurement of point cloud; point cloud slicing; multi-contour segmentation; Point Inclusion in Polygon (PIP) algorithm; nearest point search method

This work is partially supported by Key Research and Development Project of Science and Technology Department of Sichuan Province （22ZDYF3012）， Sichuan Higher Education Talent Training Quality and Teaching Reform Project （JG2021-36）， Sichuan University Science Characteristic Direction Cultivation Program （2020SCUNL204）， Sichuan University Postgraduate Education and Teaching Reform Research Project （GSSCU2021020）.

ZHANG Jin， born in 1998， M. S. candidate. His research interests include point cloud analysis， structured light three-dimensional imaging and its applications.

XU Wen， born in 1992， Ph. D. candidate. Her research interests include structured light three-dimensional imaging and its applications， artificial intelligence.

ZHOU Yuqiao， born in 1988， Ph. D. His research interests include X-ray crystallography， structural chemistry， computational chemistry.

LIU Kai， born in 1973， Ph. D.， professor. His research interests include structured light three-dimensional imaging and its applications， computer vision， digital image/signal processing.

1001-9081（2023）10-3209-08

10.11772/j.issn.1001-9081.2022101536

2022⁃10⁃13；

2023⁃01⁃10；

四川省科技厅重点研发项目（22ZDYF3012）；四川省高等教育人才培养质量和教学改革项目（JG2021⁃36）；四川大学理科特色方向培育计划项目（2020SCUNL204）；四川大学研究生教育教学改革研究项目（GSSCU2021020）。

张瑾（1998—），男，四川南充人，硕士研究生，主要研究方向：点云分析、结构光三维成像及应用； 徐文（1992—），女（彝族），四川雅安人，博士研究生，主要研究方向：结构光三维成像及应用、人工智能； 周宇乔（1988—），男，浙江绍兴人，博士，主要研究方向：X射线晶体学、结构化学、计算化学； 刘凯（1973—），男（壮族），江苏无锡人，教授，博士生导师，博士，主要研究方向：结构光三维成像及应用、机器视觉、数字图像/信号处理。

TP301.6

A

2023⁃01⁃11。