基于优化图结构自编码器的网络表示学习

富坤，郝玉涵，孙明磊，刘赢华

基于优化图结构自编码器的网络表示学习

富坤*，郝玉涵，孙明磊，刘赢华

（河北工业大学 人工智能与数据科学学院，天津 300401）（ ∗ 通信作者电子邮箱fukun@hebut.edu.cn）

网络表示学习（NRL）旨在学习网络顶点的潜在、低维表示，再将得到的表示用于下游的网络分析任务。针对现有采用自编码器的NRL算法不能充分提取节点属性信息，学习时容易产生信息偏差从而影响学习效果的问题，提出一种基于优化图结构自编码器的网络表示学习模型（NR-AGS），通过优化图结构的方式提高准确率。首先，融合结构和属性信息来生成结构和属性联合转移矩阵，进而形成高维表示；其次，利用自编码器学习低维嵌入表示；最后，通过在学习过程中加入深度嵌入聚类算法，对自编码器的训练过程和节点的类别分布划分形成自监督机制，并且通过改进的最大均值差异（MMD）算法减小学习得到的低维嵌入潜在表示层分布和原始数据分布的差距。此外，NR-AGS使用自编码器的重构损失、深度嵌入聚类损失和改进的MMD损失共同优化网络。应用NR-AGS对3个真实数据集进行学习，再使用得到的低维表示完成下游的节点分类和节点聚类任务。实验结果表明，与深度图表示模型DNGR（Deep Neural networks for Graph Representations）相比，NR-AGS在Cora、Citeseer、Wiki数据集上的Micro-F1值分别至少提升了7.2、13.5和8.2个百分点。可见，NR-AGS可以有效提升NRL的学习效果。

网络表示学习；属性信息；自编码器；深度嵌入聚类；最大均值差异

0 引言

随着信息技术的广泛使用，分析社交网络、生物网络和引文网络等信息网络能够提取社会生活的各方面潜在的信息，在许多学科的各种新兴应用程序中发挥着重要的作用［1-3］。例如，在社交网络中，将用户分类为不同的社会群体有助于现实中的一些任务，如用户搜索、有针对性的广告和推荐等；在通信网络中，检测网络的社区结构可以帮助更好地理解谣言的传播过程。然而，对这些网络的有效分析依赖于网络的表示学习［4］。

网络表示学习（Network Representation Learning， NRL）的目的是学习网络顶点的潜在、低维嵌入表示，同时保留网络拓扑结构、顶点内容和其他边信息［5］。在学习了新的顶点低维嵌入表示后，可以轻松有效地执行网络分析任务，如节点聚类、节点分类、链路预测等［6］。相关NRL模型有：基于结构信息的模型，如DeepWalk［7］、Node2Vec［8］、DNGR（Deep Neural Networks For Graph Representations）［9］、O2MAC （One2Multi graph Autoencoder for multi-view graph Clustering）［10］等；基于结构和属性信息的模型，如TADW （Text-Associated DeepWalk）［11］、DFCN（Deep Fusion Clustering Network）［12］、变分图自动编码器（Variational Graph Auto-Encoder， GVAE）［13］等。但是，当前的NRL方法存在以下两个关键问题：1）网络中的属性信息可以补偿结构信息，因此有效提取属性信息是很重要的［14］；2）在生成低维表示的学习过程中存在一定的信息偏差，影响网络表示学习的效果。

针对以上问题，本文提出了基于优化图结构自编码器的网络表示学习模型（Network Representation learning model based on Autoencoder with optimized Graph Structure， NR-AGS），该模型能够充分利用网络中的结构和属性信息，提高网络节点的聚集性，减小低维嵌入表示与原始数据分布的差距，优化低维表示空间的结构。

本文主要工作如下：

1）通过随机游走算法，将结构和属性信息联合形成结构和属性联合转移矩阵PPMI（Positive Pointwise Mutual Information），该矩阵使结构和属性信息的联系更加紧密，并且相互补充、制约，能够更加充分利用网络的信息学习。

2）在运用自编码器（Autoencoder）学习低维嵌入表示时，引入深度嵌入聚类损失和改进的最大均值差异（Maximum Mean Discrepancy， MMD）损失共同训练网络。深度嵌入聚类损失使学习得到的数据中同类别的节点更加聚集，将聚类和自动编码器统一在一个框架中。使用聚类分布指导网络表示的学习，反之，低维嵌入目标也监督聚类的生成，形成自监督机制，利用该机制优化网络结构，增强网络表示学习的效果。改进的MMD损失使学习到的低维嵌入表示分布更加接近原始数据分布，有利于保持它们的一致性。

3）运用NR-AGS学习的低维嵌入在Cora（https：//linqs-data.soe.ucsc.edu/public/lbc/cora.tgz）、Citseer（https：//linqs-data.soe.ucsc.edu/public/lbc/citeseer.tgz）、Wiki（https：//dumps.wikimedia.org/wikidatawiki/entities/）这3个公开经典数据集上的下游任务结果表明了NR-AGS的有效性，提升了网络表示学习的结果。

1 相关工作

给定一个信息网络（，，，），其中：是节点集合，是边集合，是节点属性，是节点标签。网络表示学习研究的目标是：面对大规模并且稀疏的网络，设计能够满足保留网络的局部和全局结构，并有效利用顶点属性信息，最终得到的节点低维嵌入表示能够高效地完成下游网络分析任务，如节点分类、节点聚类、社区检测等。

一部分网络表示学习模型只学习结构信息：DeepWalk［7］利用随机游走将网络嵌入问题转化为一个词嵌入问题；Node2Vec［8］在DeepWalk的基础上增加了广度优先和深度优先以探索不同的节点邻域，既考虑了局部信息又考虑了宏观的信息，具有很高的适应性；DNGR［9］运用随机游走算法计算节点拓扑结构的高维表示，再输入去噪自编码器学习低维表示；LINE（Large-scale Information Network Embedding）［14］不再采用随机游走的方法，它在图上定义了两种相似度——一阶相似度和二阶相似度，并基于这两种相似度获得节点表示；GraRep（learning Graph Representations with global structural information）［15］改进LINE，提出一种获取阶关系信息的图表示方法，可以更好地获得节点的高阶信息；SDNE（Structural Deep Network Embedding）［16］通过深层神经网络自编码器实现学习网络节点表示，直接将一阶相似度和二阶相似度保留在嵌入表示中。

上述模型都只使用了拓扑结构信息，但是真实的社会网络不仅有结构信息，还有丰富的属性信息，属性信息可以补偿结构信息：TADW［11］运用矩阵分解的方法结合属性信息和结构信息；AANE（Accelerated Attributed Network Embedding）［17］将属性信息作为被分解的信息之一，使得矩阵分解能够受到结构和属性信息的共同影响；DVNE（Deep Variational Network Embedding in Wasserstein space）［18］在SDNE的基础上考虑属性信息并提出了一种新的度量，相较于SDNE学习效果更好；ANAE（Attributed Network Auto-Encoder）［19］从属性化的局部子图中聚合属性信息，并将目标节点的表示扩散到局部子图中的其他节点，以重建它们的属性，更好地获得了节点上下文信息。

为了优化网络中的结构，有些模型引用聚类思想使网络结构更加聚集，有些模型通过引入MMD损失减小目标分布和原始分布的差异优化图结构。IDEC（Improved Deep Embedded Clustering with local structure preservation）［20］显式地定义聚类损失，模拟监督深度学习中的分类误差，通过学习表示和聚类联合优化特征。结构化深度聚类网络（Structural Deep Clustering Network， SDCN）［21］结合了自动编码器和图卷积算法的优点，将结构化信息明确地应用到深度嵌入聚类中。DFCN［12］在此基础上将图结构和节点属性联合建模，并捕获了全局聚类结构。最大均值差异（MMD），即两个概率分布之间的距离度量，在MMDnets［22］中，MMD被用于直接比较生成的样本与真实样本；DSNs（Domain Separation Networks）［23］将MMD融合到编码‒解码的网络中，减小源域和目标域的差异，提高模型性能；MMD-GAN（Maximum Mean Difference-Generative Adversarial Network）［24］则将它的作为损失函数扩展到GAN框架中，明显改善性能。

根据以上研究，同时利用结构和属性信息的模型普遍比只利用单个信息的模型学习效果更好，同时在网络中融入聚类和MMD可以优化网络结构，获得更优的表示。

2 基于优化图结构自编码器

NR-AGS的总体框架如图1所示。它的设计思路如下：首先，为了充分利用结构信息和属性信息，引入了DNGR中的PPMI矩阵，并在此基础上融合了属性信息解决数据稀疏导致学习效率低的问题；其次，为了优化自编码器学习到的表示结构，在使用自动编码器学习低维嵌入表示的过程中，加入深度嵌入聚类和MMD共同优化深度网络。综上所述，本文在自编码器重构损失的基础上，添加了深度聚类损失和MMD损失两个信息约束项。

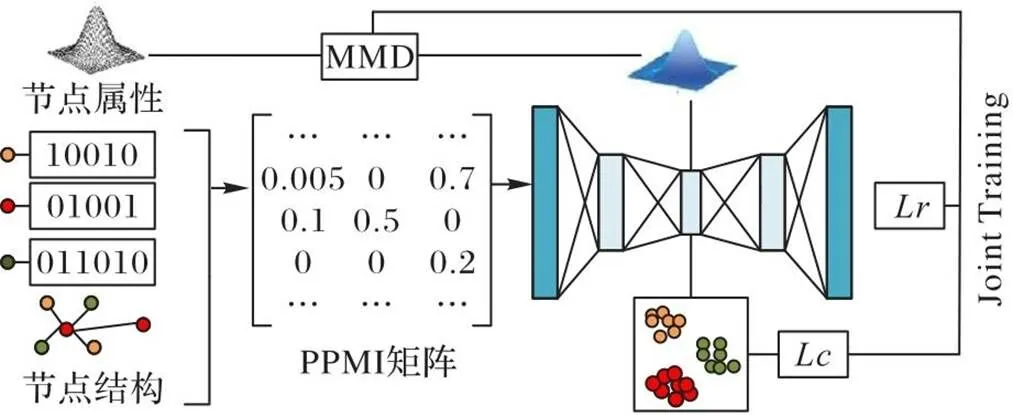
图1　NR-AGS框架

2.1　PPMI矩阵构建

DNGR通过随机游走算法构建的PPMI矩阵只融合了结构信息，本文在此基础上又融入了属性信息，利用结构和属性信息共同提取特征信息，有助于获得更好的节点表示。

在网络表示学习过程中，首先结合结构信息和属性信息形成结构‒属性联合转移矩阵，再通过随机冲浪算法形成共现概率矩阵，最后转化为高密度的PPMI矩阵。

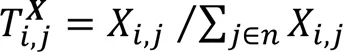
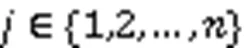
为了综合运用节点的两个信息源，结合结构转移矩阵和属性转移矩阵形成结构和属性联合转移矩阵，计算方法如下：

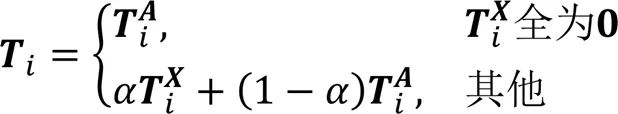
其中：表示各个转移矩阵的第行；（0<<1）为平衡系数。该联合方法通过以下方法使属性网络更加密集：1）如果在网络中两个节点间没有连边，但是它们的前个的节点属性相似，则它们之间就会连上一条新边，使网络之间联系更加紧密；2）如果两个节点已经存在连边，则将通过参数（0<<1）平衡结构和属性信息在运用中的比重，值越小，属性信息对最终的节点低维表示的影响越大［9］。

其次，沿用DNGR中的两个步骤：1）通过步迭代，每次以的概率随机冲浪转化为共现概率矩阵；2）通过共现概率矩阵构造信息率密度较高的PPMI矩阵。

2.2　基于最大均值差异的结构优化

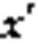
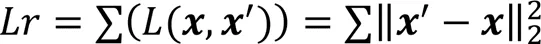
本文通过引入改进的MMD度量低维嵌入表示和输入之间的差异，通过减小该差异优化自编码器学到的低维嵌入表示。编码器的中间层的潜在低维嵌入表示会保存原始数据的重要信息，从而形成两个不同但相关的域，即源域（原始数据分布）和目标域（编码器中间的低维嵌入表示分布），即最小化源域和目标域的差异，使目标域的结果更加准确。MMD就是通过核函数将一个分布映射到再生希尔伯特空间上，之后度量在再生希尔伯特空间中两个分布的距离。MMD的损失如下：

其中：sup表示求上界；E表示求期望；（∙）表示映射函数，函数指在再生希尔伯特空间中的范数应该小于等于1；在本文中指原始数据，指编码器产生的低维嵌入表示。MMD的核函数是高斯核函数：

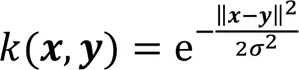
由于高斯核函数是非线性的，耗时长，所以本文对它进行改进，运用线性的二次有理核代替高斯核函数提高运算效率，改进的二次有理核通常具有和高斯核函数相同的效果，核函数如下所示：

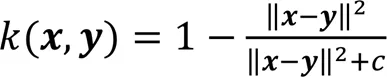
其中为二次有理核的超参数：较小的会使决策表面更平滑；较高的使结果更加准确，但可能会过拟合。在实际应用中会取多个值，分别求核函数后再取和，作为最后的核函数［26］。

本文通过引入改进的MMD使得两个域之间的差距越来越小，使编码器的低维嵌入表示越来越准确。其中，核方法的非线性映射具有面向具体应用问题设计的特性，因此便于集成问题相关的先验知识；此外，线性学习器相较于非线性学习器具有更好的过拟合控制，可以更好地保证泛化性能。综上，选择MMD有明显的优势。

2.3　基于深度聚类的结构优化

在网络中节点结构间具有内聚的宏观特性，同类节点之间距离较近，不同类节点距离较远，为了使得本文利用自编码器学习节点的低维嵌入表示更加准确地反映这种宏观特性，优化节点结构，需要增强网络结构中节点的内聚性。本文在编码过程中引入深度嵌入聚类算法指导监督编码器，深度嵌入聚类作用在深度神经网络形成的低维嵌入表示空间，具体步骤［27］如下。

1）计算由t分布测量的软标签分配矩阵。先运用传统的-means算法求出聚类第个中心，q是以t分布测量的空间中的第个样本与第个聚类中心的的相似性度量，又称为软标签概率，q真实地反映了节点的数据类分布概率。q组成的矩阵即为∈R，为节点总数，为数据集类目数目。q的计算公式如下：

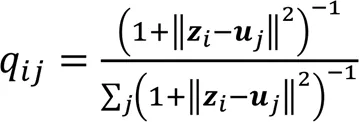
3）计算和的KL散度。在求得的软标签分配概率矩阵和目标分布概率矩阵后，运用KL散度（Kullback-Leibler Divergence）衡量它们之间的差距。KL散度可以衡量在选择近似分布时损失的信息量，KL散度值越小，表示和的差距越小，越真实地衡量目标分布。聚类损失的计算公式如下。

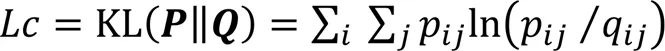
量化聚类损失是深度嵌入聚类的核心步骤，将加入统一的损失函数中训练深度神经网络，进一步强化监督低维嵌入表示的生成。在网络训练过程中，通过调整，使得更好地衡量真实的数据分布，更新低维嵌入表示空间的聚类中心和深度神经网络的参数，使得该表示空间每个类中的样本分布更加密集［28］。

2.4　NR-AGS总体设计

NR-AGS在训练过程中共考虑3部分损失：自动编码器重构损失、MMD损失和聚类损失。自编码器用于学习低维嵌入表示，学习到的低维表示可以较好地保留数据中的信息；MMD损失可以减小原始数据分布和编码器中间的低维嵌入表示分布之间的差异；聚类损失可以调整嵌入空间的结构达到聚类效果，有利于学习到的低维嵌入的节点分布更加清晰，更好地体现网络中节点间具有社区内聚的宏观特性。NR-AGS的整体损失如下：

其中：和分别为深度嵌入聚类损失和MMD损失的权重。使用深度嵌入聚类损失和改进的MMD损失共同优化深度神经网络，可以得到更加准确的低维嵌入表示。算法伪代码如算法1所示。

算法1 NR-AGS。

输入 邻接矩阵、属性信息矩阵、平衡系数、Top-值、随机冲浪迭代步数、重启概率、嵌入空间维度、簇中心个数、迭代次数；

输出 特征向量矩阵。

1）初始化模型所有权重矩阵

8） for=1 todo

12） end for

由上面分析可以得出，NR-AGS的时间复杂度主要取决于PPMI矩阵、自编码器、深度嵌入聚类和改进的MMD，令为低维嵌入维度，则NR-AGS的时间复杂度为（2）。

3 实验与结果分析

为了测试NR-AGS的性能，将本文模型与几种常用的方法在3个真实网络数据集上进行比较，通过本文模型和它的变体学习的低维嵌入表示在下游任务的实验，验证本文模型在网络表示学习方面的有效性。

本文实验环境是基于64核、内存4 GB的CPU环境，编程语言为Python3.6，实验框架为PyTorch1.8.1。

3.1　实验设置

3.1.1数据集

本文选取研究网络表示学习时常用的数据集进行实验，分别是两个引文网络数据集Cora、Citeseer和一个网页网络数据集Wiki。

Cora数据集包含2 708篇机器学习论文和论文间的5 429篇链接，这些链接是文档之间的引用关系，每个节点的属性信息对应每篇论文的一个1 443维向量表示，节点的标签按论文研究领域分为7个类别，分别为神经网络、遗传算法、基于案例、概率方法、强化学习、规则学习和理论。

Citeseer数据集包含3 312篇论文、4 732个链接和1 433个属性，节点的标签按论文研究领域分为数据库、机器学习、代理、信息检索、人工智能和人机交互这6类。

Wiki数据集是一个包含2 405个网页和12 761个链接的网页网络数据集，每个网页表示一个节点，节点之间的边是连接到其他网页的超链接，每个网页的文本内容作为该网页的属性信息。按网页类别赋予不同的标签，如艺术、历史、科学等，共17类。相较于Cora和Citeseer数据集，Wiki数据集的节点数少、连接多、类别多。具体数据信息如表1所示。

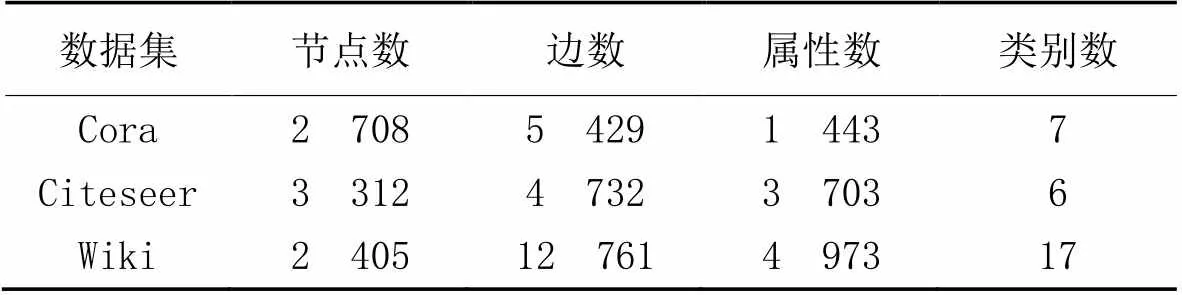
表1　网络数据集详情

3.1.2基准方法

本文运用SVD（Singular Value Decomposition）算法进行只利用网络中属性信息的网络表示学习。与经典的网络表示学习算法对比：1）DeepWalk［7］将网络嵌入问题转化为一个词嵌入问题；2）Node2Vec［8］通过增加广度优先和深度优先探索不同的节点邻域，既考虑了局部信息又考虑了宏观的信息，具有很高的适应性；3）DNGR［9］首先运用随机冲浪算法获取网络的高维节点表示，其次使用去噪自编码器学习节点的低维表示，但只融合了结构信息。

其他对比的先进网络表示学习算法：1）TADW［11］是基于矩阵分解形式的DeepWalk算法，并在训练过程中融合了节点的属性信息；2）AANE［17］将属性信息作为被分解的信息之一，使得学习到的表示结果能够保持结构上距离相近和属性相似的节点向量表示比较接近；3）ANAE［19］通过从属性化的局部子图中聚合属性信息重建属性，获得了节点上下文信息；4）DFCN［12］利用深度嵌入聚类形成三重监督机制，能更有效地融合网络中的信息，优化网络结构；5）dSAFNE（dynamic Structure and vertex Attributes Fusion Network Embedding）［29］通过引入了一种属性驱动的拉普拉斯空间优化方法收敛结构特征提取和属性特征提取的过程，使得具有相似属性但拓扑距离较远的顶点在嵌入空间中也保持相邻。

3.1.3实验参数设置

由于DNGR也是网络表示学习模型，同时也可将此模型用于本文实验的数据集（具体情况可见文献［30］），本文实验也符合DNGR的环境，所以结构属性联合转移矩阵时使用的属性相似性调整参数Top-、平衡结构和属性信息的超参数、随机冲浪算法形成共现概率矩阵的重启概率参数、随机冲浪算法每次迭代步数的参数设置沿用DNGR模型相同的设置［9］。改进的MMD部分核函数的超参数，该参数在实际应用中会取多个值，本文取值集合为｛2××0.1，2××0.2，2××0.5，2××1，2××2，2××5，2××10｝，为自编码器形成的低维嵌入维度，再分别按照式（13）求出核函数，将所得的核函数求和，作为最后的核函数。深度嵌入聚类损失权重和MMD损失权重在模型运行中影响的具体分析见3.6节。

3.2　节点分类实验

节点分类是评价网络表示学习模型的一个重要下游任务，本文在3个数据集上先运用本文模型学习低维嵌入表示之后，再进行下游节点分类的实验。在节点分类实验中抽出一定比率带标记的节点嵌入表示，作为训练集，其余作为测试集，其中训练集比例分别为10%、30%、50%、70%、90%，做10次实验，实验结果取均值。表2～4中分别为不同模型在3个数据集节点分类任务中的Micro-F1指标的结果。

从表2～3可以看出，在Cora和Citeseer数据集上，在不同比例的训练集下，NR-AGS均优于基准方法；从表4可以看出，在Wiki数据集上训练比例为10%和50%时，NR-AGS的Micro-F1值略差于其他对比基准模型，其余训练比例的Micro-F1值均优于其他对比基准模型。具体地，与DNGR相比，在Cora、Citeseer和Wiki数据集上，NR-AGS的Micro-F1分别提升了7.2～8.8、13.5～25.3和8.2～12.1个百分点。

数据结果显示，由于NR-AGS有效地结合了节点结构和属性信息，使得它们相互补充和制约；联合深度嵌入聚类损失共同优化网络，使得不同类别节点分布更加聚集；引入MMD损失，使得学习到的低维嵌入表示能够更加接近真实的数据。通过以上两个损失约束使得NR-AGS取得了比其他基准模型在大多数节点分类的实验中更好的效果并且较为稳定。由于Wiki数据集类别较多，数据较复杂，对节点分类的效果有一定的影响，NR-AGS的学习效果存在个别不稳定的情况。

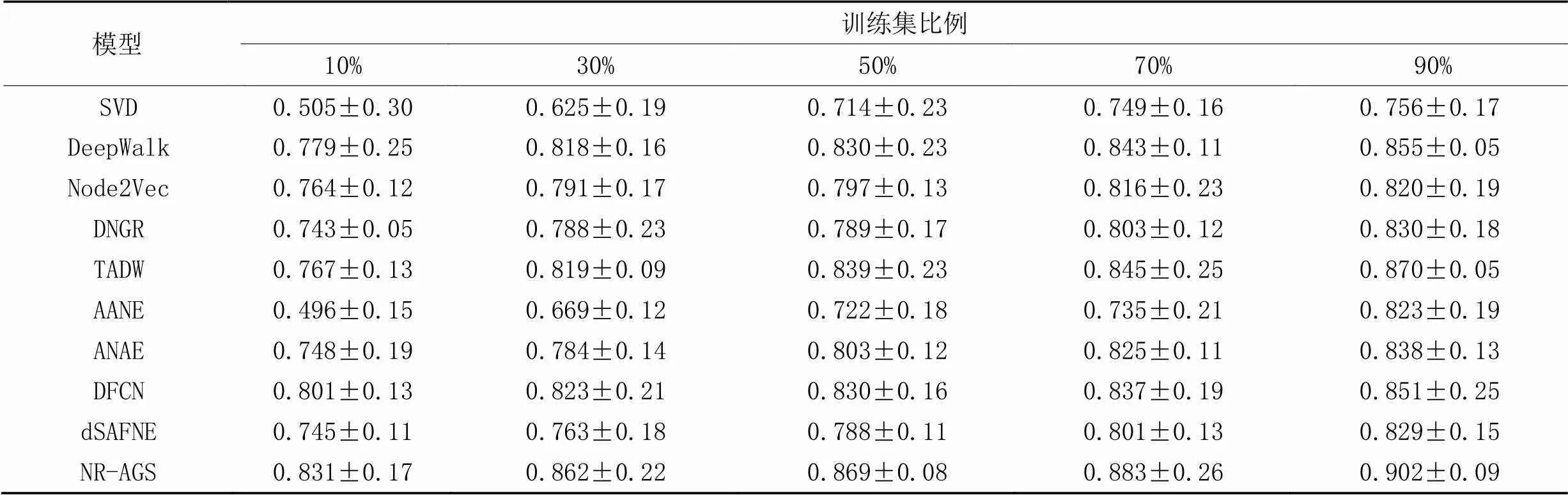
表2　Cora数据集上的节点分类结果的Micro-F1值

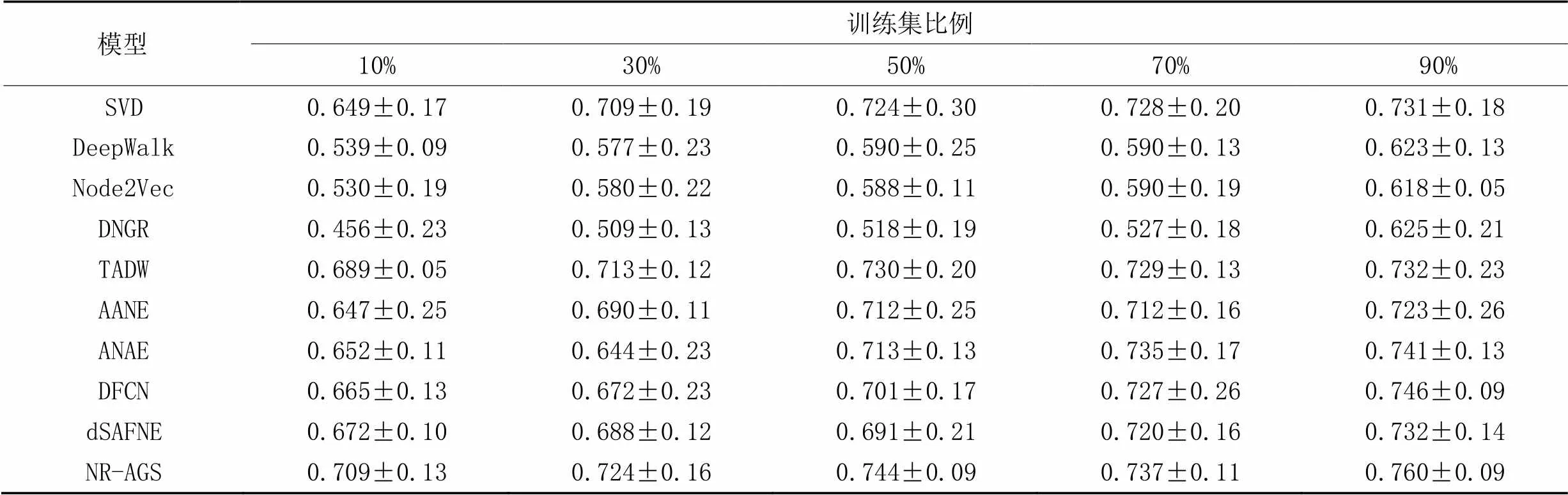
表3　Citeseer数据集上的节点分类结果Micro-F1值

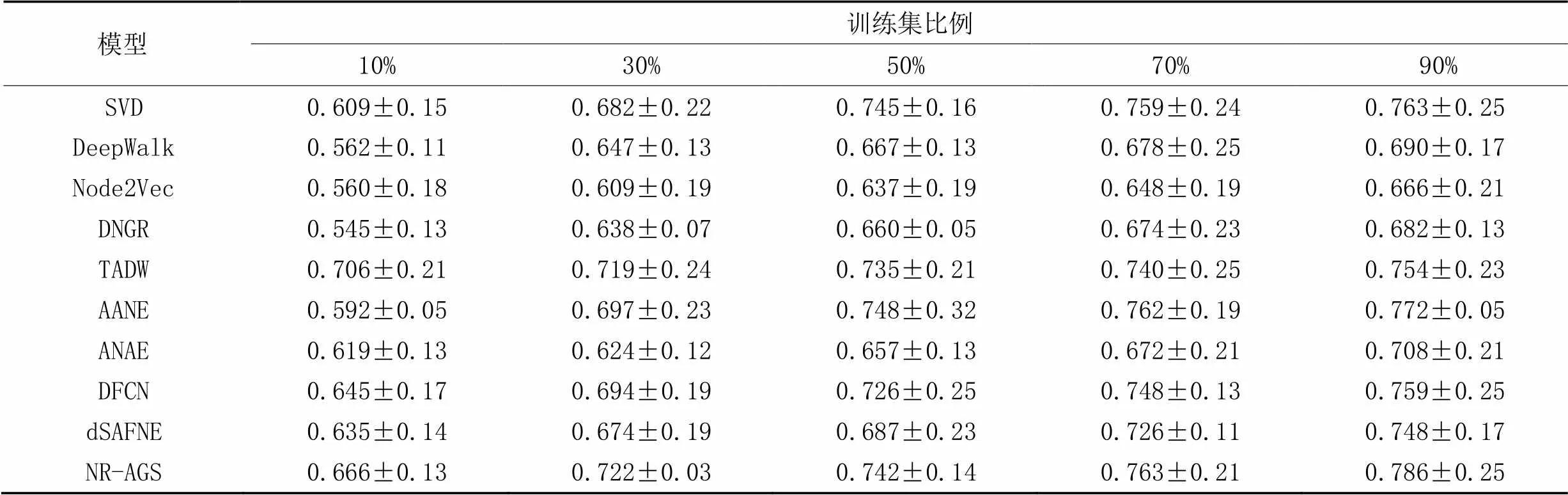
表4　Wiki数据集上的节点分类结果的Micro-F1值

3.3　可视化实验

本节运用t-SNE（t-distributed Stochastic Neighbor Embedding）工具［31］可视化Cora和Citeseer数据集的下游节点分类实验结果。图2展示了DeepWalk、TADW、AANE和NR-AGS在Cora数据集上的效果，其中，不同颜色的点表示数据集的不同类别。Cora数据集有7个类别，从图2可以看出，DeepWalk各个类别的数据点界限不清晰，分布较为混乱，而TADW、AANE的每个类别的分布结果较平均，但是边界不够清晰，而NR-AGS能够清晰地体现每类数据的界限，对应结构更紧凑，呈现较好的可视化效果。图3展现了上述4种模型在Citeseer数据集上的可视化效果，Citeseer具有6个类别，从图3可以看出，DeepWalk、TADW、AANE的图示中各个类别节点分布混乱，边界也不清晰，而NR-AGS呈现出同类节点明显聚集的效果。从上述可视化的实验结果可以看出，NR-AGS由于引入了深度嵌入聚类与自编码器形成自监督，在学习的过程中优化了图结构，使网络中节点的聚集性更加显著，可视化效果优于其他基准模型。

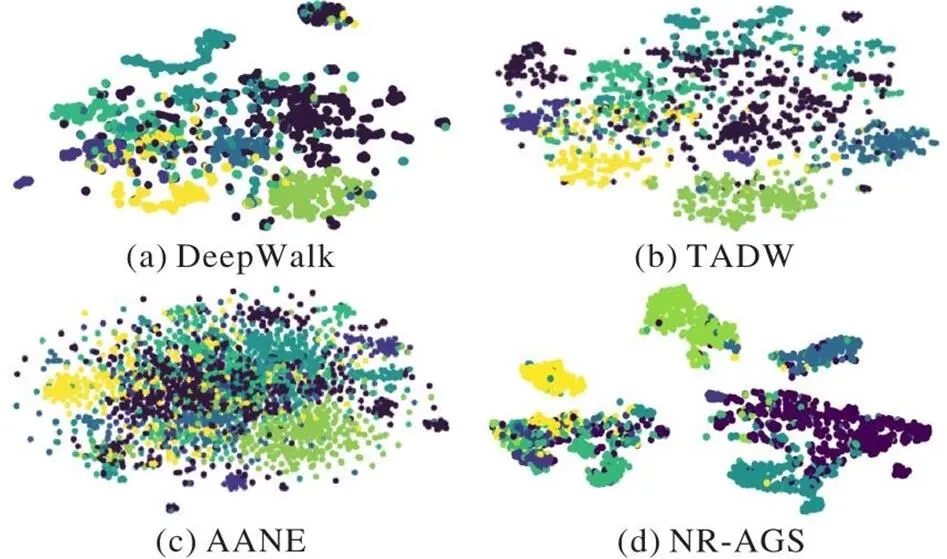
图2　Cora数据集的可视化

图3　Citeseer数据集的可视化

3.4　消融实验

为了验证添加深度嵌入聚类损失和改进的MMD损失的有效性，本节提出3个NR-AGS的变体模型，进行消融实验。3个NR-AGS的变体模型分别为：1）NR-AGS-a，表示无深度嵌入聚类损失和MMD损失；2）NR-AGS-ac，表示仅使用深度嵌入聚类损失；3）NR-AGS-am，表示仅使用MMD损失。NR-AGS表示同时使用深度嵌入聚类损失和MMD损失的完全体。分别在3个数据集上先运用上述4种模型学习低维嵌入表示之后，进行训练集比例为50%的节点分类实验，Micro-F1、Macro-F1作为评价指标，实验结果如表5所示。

从表5可以看出：

1）在Cora和Citeseer数据集上，同时使用深度嵌入聚类损失和MMD损失的完全体NR-AGS的Micro-F1、Macro-F1值均优于其他3个变体模型，表明了同时使用这两种约束会提升模型的分类性能。

2）在Wiki数据集上的节点分类实验中，同时使用深度嵌入聚类损失和MMD损失的完全体NR-AGS的Micro-F1、Macro-F1值低于NR-AGS-ac、NR-AGS-am；这是因为Wiki数据集较大，类别数较多，影响深度嵌入聚类损失和MMD损失共同约束的效果，调参更加复杂，导致共同约束的节点分类效果较不稳定。

3）NR-AGS-ac、NR-AGS-am和NR-AGS在所有数据集上的节点分类结果均优于NR-AGS-a，表明了单独使用或同时使用两个约束均会提升模型的分类性能，结果验证了这两个损失约束的有效性。

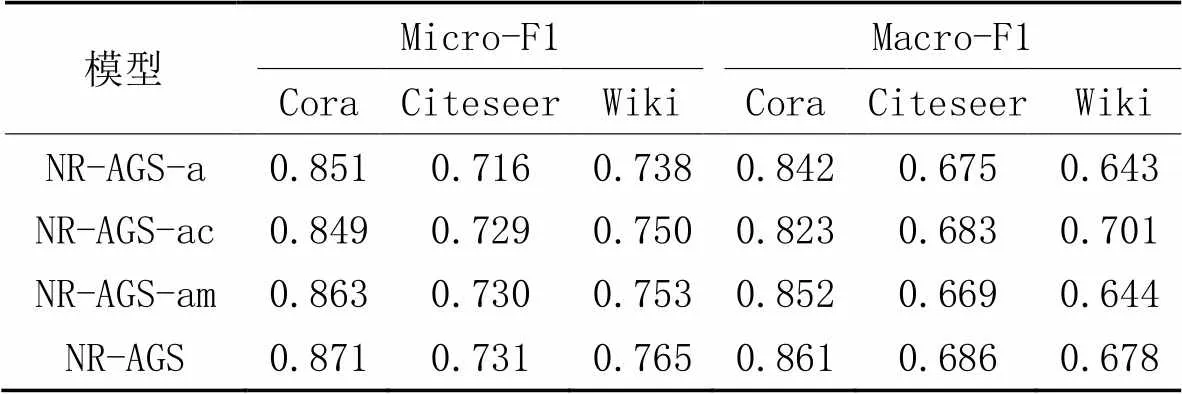
表5　NR-AGS及其变体模型的节点分类结果

3.5　节点聚类实验

在3个数据集上先运用本文模型学习得到低维嵌入表示之后，再进行下游节点聚类［32］的实验，评估指标选用标准化互信息（Normalized Mutual Information， NMI）和正确率（ACC），实验结果如图4所示。从图4中可以得出以下结论：1）利用节点结构信息和属性信息的网络表示学习模型大部分比只运用节点结构信息的模型能获得更好的节点聚类效果，说明节点属性信息能为节点聚类任务提供有效支持信息；2）相较于其他利用了结构和属性信息的基准模型，NR-AGS取得了更好或者相当的效果，说明NR-AGS可以获得更高质量的节点低维嵌入表示，进而有益于节点聚类任务。

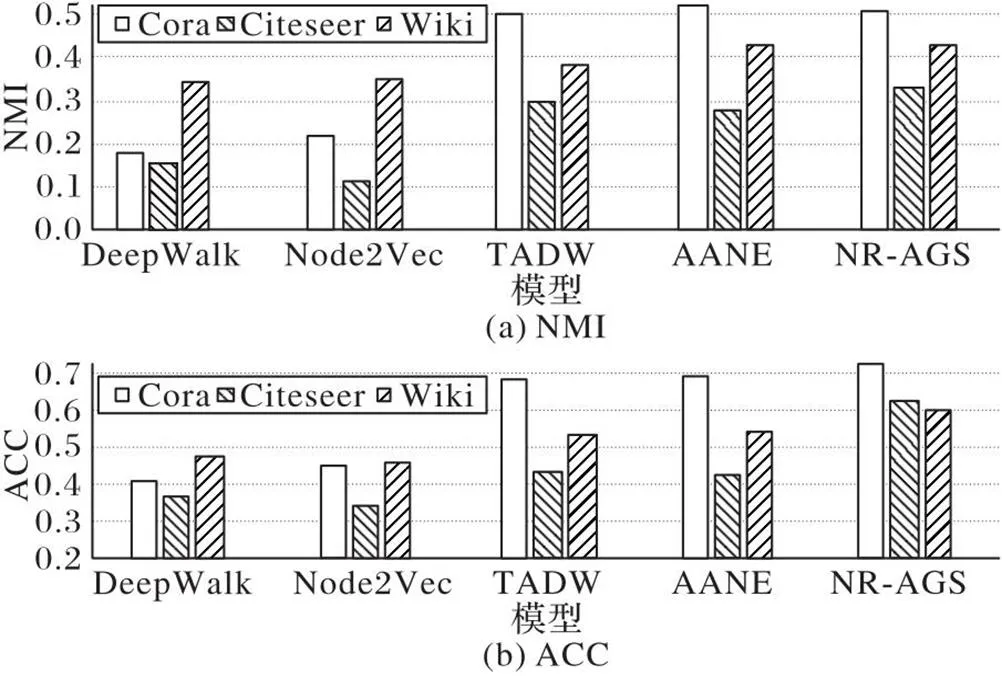
图4　在3个数据集上的节点聚类结果

3.6　参数敏感性分析

本节通过实验分析NR-AGS中自编码器的低维嵌入表示的维数、MMD的参数、深度嵌入聚类损失权重和MMD损失权重对下游节点分类任务性能的影响。当分析一个参数时，固定其他非分析参数，改变该分析参数的数值研究它的影响。

自编码器生成的低维嵌入表示的维度对模型的学习效果有一定的影响，在3个数据集上先运用本文模型学习低维嵌入表示之后，再进行下游节点分类的实验。训练集比例为50%，Micro-F1作为评价指标，分别设置=64、128、192、256、320、324、448、512维，结果如图5（a）所示。从图5（a）可以看出，Micro-F1值逐渐上升，但在256维时，存在较为明显的拐点，即当低维嵌入表示的维度高于256维时，节点分类的效果没有稳步上升，反而有所下降。由实验结果可知NR-AGS在=256时性能较好。

MMD的参数依照DSNs中的经验，较小的会使决策表面更平滑，而较大的使结果更加准确，但可能过拟合。为了保持稳定性，在实际应用中会取多个值，分别求核函数。本文实验中以维度的两倍为基数，以1为中心点，取｛0.1，0.2，0.5，1，2，5，10｝，再另=｛0.1，0.2，0.5，1，2，5，10｝形成多核进行网络学习，从图5（b）中可以看出，当取时，实验结果比取单个核函数效果更好。

图5（c）显示深度嵌入聚类损失权重对节点分类性能的影响，实验中将它的取值从0.01调整到10。可以发现，在3个数据集上，随着权重的增加，NR-AGS的Micro-F1值会发生变化，说明模型对参数的敏感性较高。综合考虑，在深度嵌入聚类损失的权重取1时，在3个数据集上的节点分类性能都相对较好。

图5（d）展示了MMD损失权重对模型节点分类性能的影响。在10-3至103时，NR-AGS的分类表现都较稳定，说明NR-AGS对参数的敏感性较低。在3个数据集上，取值为1时，模型分类效果较好。

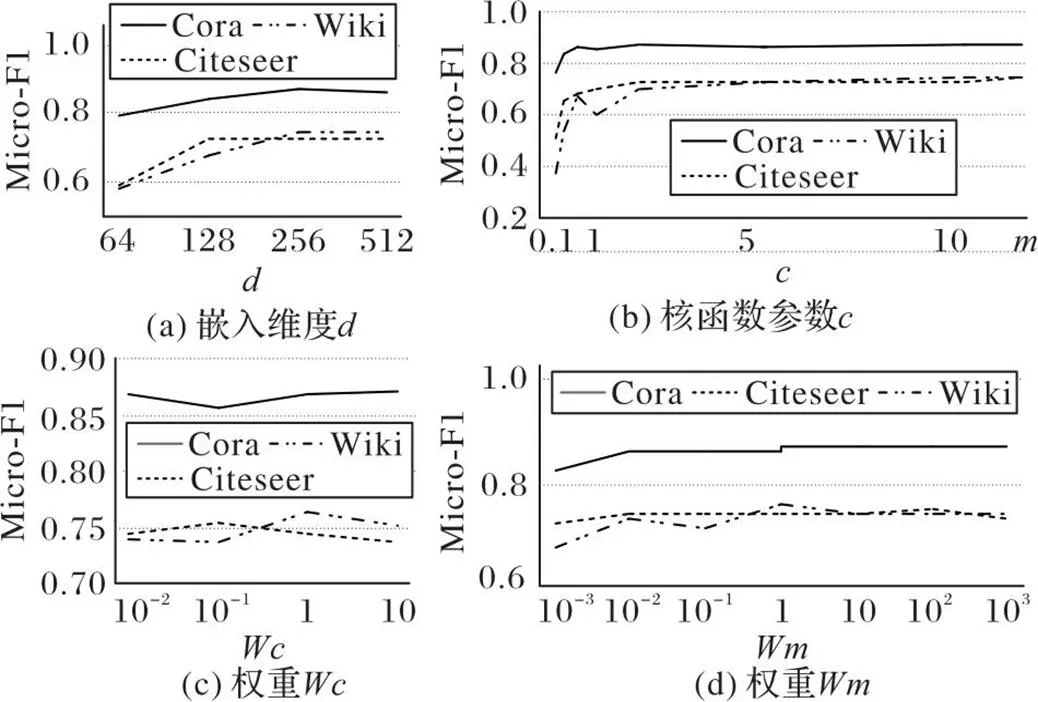
图5　不同参数对Micro-F1值的影响

4 结语

为了充分利用网络中的结构和属性信息，本文提出基于优化图结构自编码器的网络表示学习模型（NR-AGS）。引入PPMI矩阵将结构和属性信息相融合，得到数据的高维嵌入表示，再利用自编码器学习低维嵌入表示，在学习过程中融合深度嵌入聚类和改进的最大均值差异共同优化学习过程。使用NR-AGS学习得到的低维嵌入表示进行下游的节点分类实验、可视化实验和节点聚类等实验，实验结果验证了NR-AGS具有较好的网络表示学习效果。实验结果表明使用PPMI矩阵将结构和属性信息结合的学习方法能更加高效率地利用网络的真实信息，在学习过程中融合聚类算法可以更好地使用数据分布的内聚性优化数据结构，改进的最大均值差异使学习到的低维嵌入表示更加接近真实数据，通过联合优化以上3种损失，改善了学习到的低维表示在下游任务上的性能。在未来的研究中，可以将该模型进一步应用于大规模的网络数据，还可以将模型应用于稀疏或缺失数据集，进一步改进模型，提高它的学习能力。

[1] 孙金清，周慧，赵中英. 网络表示学习方法研究综述［J］. 山东科技 大学学报（自然科学版）， 2021， 40（1）：117-128.（SUN J Q， ZHOU H， ZHAO Z Y. A survey of network representation learning methods［J］. Journal of Shandong University of Science and Technology （Natural Science）， 2021， 40（1）： 117-128.）

[2] ZHANG D， YIN J， ZHU X， et al. Network representation learning： a survey［J］. IEEE Transactions on Big Data， 2020， 6（1）： 3-28.

[3] WU Z， PAN S， CHEN F， et al. A comprehensive survey on graph neural networks［J］. IEEE Transactions on Neural Networks and Learning Systems， 2021， 32（1）： 4-24.

[4] HOU Y， CHEN H， LI C， et al. A representation learning framework for property graphs［C］// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2019： 65-73.

[5] AHMED N K， ROSSI R A， LEE J B， et al. Role-based graph embeddings［J］. IEEE Transactions on Knowledge and Data Engineering， 2022， 34（5）： 2401-2415.

[6] 刘昱阳，李龙杰，单娜，等. 融合聚集系数的链接预测方法［J］. 计算机应用， 2020， 40（1）： 28-35.（LIU Y Y， LI L J， SHAN N， et al. Link prediction method fusing clustering coefficients［J］. Journal of Computer Applications， 2020， 40（1）： 28-35.）

[7] PEROZZI B， AL-RFOU R， SKIENA S. DeepWalk： online learning of social representations［C］// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2014： 701-710.

[8] GROVER A， LESKOVEC J. node2vec： scalable feature learning for networks［C］// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 855-864.

[9] CAO S， LU W， XU Q. Deep neural networks for learning graph representations［C］// Proceedings of the 30th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2016： 1145-1152.

[10] FAN S， WANG X， SHI C， et al. One2Multi graph autoencoder for multi-view graph clustering［C］// Proceedings of the Web Conference 2020. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2020： 3070-3076.

[11] YANG C， LIU Z， ZHAO D， et al. Network representation learning with rich text information［C］// Proceedings of the 24th International Joint Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2015： 2111-2117.

[12] TU W， ZHOU S， LIU X， et al. Deep fusion clustering network［C］// Proceedings of the 35th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2021： 9978-9987.

[13] BEHROUZI T， HATZINAKOS D. Graph variational auto-encoder for deriving EEG-based graph embedding［J］. Pattern Recognition， 2022， 121： No.108202.

[14] TANG J， QU M， WANG M， et al. LINE： large-scale information network embedding［C］// Proceedings of the 24th International Conference on World Wide Web. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2015：1067-1077.

[15] CAO S， LU W， XU Q. GraRep： learning graph representations with global structural information［C］// Proceedings of the 24th ACM International Conference on Information and Knowledge Management. New York： ACM， 2015： 891-900.

[16] WANG D， CUI P， ZHU W. Structural deep network embedding［C］// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 1225-1234.

[17] HUANG X， LI J， HU X. Accelerated attributed network embedding［C］// Proceedings of the 2017 SIAM International Conference on Data Mining. Philadelphia， PA： SIAM， 2017：633-641.

[18] ZHU D， CUI P， WANG D， et al. Deep variational network embedding in Wasserstein space［C］// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2018： 2827-2836.

[19] CEN K， SHEN H， GAO J， et al. ANAE： learning node context representation for attributed network embedding［EB/OL］. （2020-07-06） ［2022-07-12］. https：//arxiv.org/pdf/1906.08745.pdf.

[20] GUO X， GAO L， LIU X， et al. Improved deep embedded clustering with local structure preservation［C］// Proceedings of the 26th International Joint Conference on Artificial Intelligence. California： ijcai.org， 2017： 1753-1759.

[21] YANG Y. SDCN： a species-disease hybrid convolutional neural network for plant disease recognition［C］// Proceedings of the 2022 International Conference on Artificial Neural Networks， LNCS 13532. Cham： Springer， 2022： 769-780.

[22] LI Y， SWERSKY K， ZEMEL R. Generative moment matching networks［C］// Proceedings of the 32nd International Conference on Machine Learning. New York： JMLR.org， 2015： 1718-1727.

[23] BOUSMALIS K， TRIGEORGIS G， SILBERMAN N， et al. Domain separation networks ［C］// Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2016： 343-351.

[24] WANG W， SUN Y， HALGAMUGE S. Improving MMD-GAN training with repulsive loss function［EB/OL］ （2019-02-08） ［2022-07-12］.https：//arxiv.org/pdf/1812.09916，pdf.

[25] KINGMA D P， WELLING M. Auto-encoding variational Bayes［EB/OL］. （2014-05-01） ［2022-07-12］.https：//arxiv.org/pdf/1312.6114.pdf.

[26] TZENG E， HOFFMAN J， ZHANG N， et al. Deep domain confusion： maximizing for domain invariance［EB/OL］. （2014-12-10） ［2022-07-12］.https：//arxiv.org/pdf/1412.3474.pdf.

[27] TANG Y， REN F， PEDRYCZ W. Fuzzy C-Means clustering through SSIM and patch for image segmentation［J］. Applied Soft Computing， 2020， 87： No.105928.

[28] 尤坊州，白亮. 关键节点选择的快速图聚类算法［J］. 计算机科学与探索， 2021， 15（10）： 1930-1937.（YOU F Z， BAI L. Fast graph clustering algorithm based on selection of key nodes［J］. Journal of Frontiers of Computer Science and Technology， 2021， 15（10）： 1930-1937.）

[29] HU S， ZHANG B， LV H， et al. Improving network representation learning via dynamic random walk， self-attention and vertex attributes-driven Laplacian space optimization［J］. Entropy， 2022， 24（9）： No.1213.

[30] 张蕾，钱峰，赵姝，等. 利用变分自编码器进行网络表示学习［J］. 计算机科学与探索， 2019， 13（10）：1733-1744.（ZHANG L， QIAN F， ZHAO S， et al. Network representation learning via variational auto-encoder［J］. Journal of Frontiers of Computer Science and Technology， 2019， 13（10）：1733-1744.）

[31] WANG Y， SONG Z， ZHANG R， et al. An overview of t-SNE optimization algorithms［J］. International Core Journal of Engineering， 2021， 7（2）： 422-432.

[32] LI X， KAO B， REN Z， et al. Spectral clustering in heterogeneous information networks［C］// Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2019： 4221-4228.

Network representation learning based on autoencoder with optimized graph structure

FU Kun*， HAO Yuhan， SUN Minglei， LIU Yinghua

（，，300401，）

The aim of Network Representation Learning （NRL） is to learn the potential and low-dimensional representation of network vertices， and the obtained representation is applied for downstream network analysis tasks. The existing NRL algorithms using autoencoder extract information about node attributes insufficiently and are easy to generate information bias， which affects the learning effect. Aiming at these problems， a Network Representation learning model based on Autoencoder with optimized Graph Structure （NR-AGS） was proposed to improve the accuracy by optimizing the graph structure. Firstly， the structure and attribute information were fused to generate the joint transition matrix， thereby forming the high-dimensional representation. Secondly， the low-dimensional embedded representation was learnt by an autoencoder. Finally， the deep embedded clustering algorithm was introduced during learning to form a self-supervision mechanism in the processes of autoencoder training and the category distribution division of nodes. At the same time， the improved Maximum Mean Discrepancy （MMD） algorithm was used to reduce the gap between distribution of the learnt low-dimensional embedded representation and distribution of the original data. Besides， in the proposed model， the reconstruction loss of the autoencoder， the deep embedded clustering loss and the improved MMD loss were used to optimize the network jointly. NR-AGS was applied to the learning of three real datasets， and the obtained low-dimensional representation was used for downstream tasks such as node classification and node clustering. Experimental results show that compared with the deep graph representation model DNGR （Deep Neural networks for Graph Representations）， NR-AGS improves the Micro-F1 score by 7.2， 13.5 and 8.2 percentage points at least and respectively on Cora， Citeseer and Wiki datasets. It can be seen that NR-AGS can improve the learning effect of NRL effectively.

Network Representation Learning (NRL); attribute information; autoencoder; deep embedded clustering; Maximum Mean Discrepancy (MMD)

This work is partially supported by National Natural Science Foundation of China （62072154）.

FU Kun， born in 1979， Ph. D.， associate professor. Her research interests include social network analysis， network representation learning.

HAO Yuhan， born in 1997， M. S. candidate. Her research interests include network representation learning.

SUN Minglei， born in 1992， M. S. candidate. His research interests include network representation learning.

LIU Yinghua， born in 1996， M. S. candidate. His research interests include social network analysis.

1001-9081（2023）10-3054-08

10.11772/j.issn.1001-9081.2022101494

2022⁃10⁃12；

2023⁃02⁃10；

国家自然科学基金资助项目（62072154）。

富坤（1979—），女，辽宁辽阳人，副教授，博士，主要研究方向：社会网络分析、网络表示学习； 郝玉涵（1997—），女，河北张家口人，硕士研究生，主要研究方向：网络表示学习； 孙明磊（1992—），男，河北承德人，硕士研究生，主要研究方向：网络表示学习； 刘赢华（1996—），男，河北邯郸人，硕士研究生，主要研究方向：社会网络分析。

TP391

A

2023⁃02⁃15。