数据分块算法在定位差异数据时的作用分析

黄文豪,齐德昱,谢 嵘,刘 宇,张皓同

(1.广东外语外贸大学南国商学院 数字化技术研究院,广东 广州 510545;2.华南理工大学 计算机科学与工程学院,广东 广州 510641)

0 引 言

随着数据量的快速增长,如何定位两个相似数据之间的差异数据,即差异数据定位,也得到了快速的发展。在现有的研究中,学者们多采取数据分块的方式来找出两个相似数据间不同的分块,这些分块则是差异数据。这种方式的工作过程如图1所示。具体的,首先对Data1和Data2按照相同的数据分块算法进行分块,然后比较两组分块之间不同的分块,这些不同的分块所组成的数据即为差异数据。

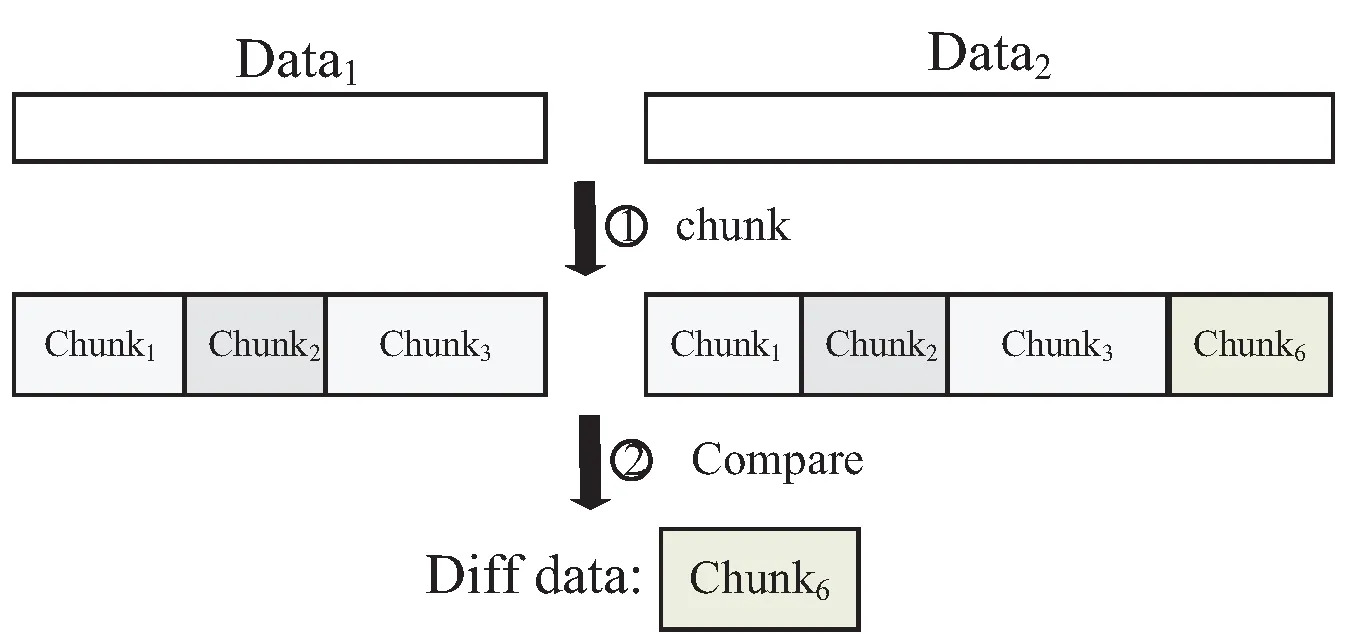
图1 差异数据定位的过程

学术界关于差异数据分块的研究重点集中在数据分块算法的设计上。数据分块算法的不同将直接影响差异数据定位的效果,比如能否全部定位出不同的数据、定位到的差异数据中相同数据的多少等。

不过学术界提出的数据分块算法都是在实验上验证算法在差异数据定位中起到的作用,并没有从理论上给出数据分块算法能否定位出所有不同的数据,也没有探讨数据分块算法中各参数在差异定位中所起到的作用。因此,该文对差异数据定位的过程进行抽象,推导出了这一过程的正确性。同时,还对数据分块算法中参数与差异数据定位的关系进行了讨论。

1 相关工作

借助数据分块算法来定位差异数据这一方法多用在重复数据删除、数据增量同步等领域。数据分块算法是对数据进行分块,通过对每个块进行处理,解决数据整体不易处理的问题,是一种化整为零的思路。该文探讨的数据差异定位主要是为了更好地应用于数据增量同步,因为重复数据删除对分块的稳定性会有额外的要求,不过该文得到的一些结论也可以在重复数据删除中起到借鉴作用。

数据分块算法最早应用在差异数据定位中是A.Tridgell提出的一种基于多轮通讯的同步算法Rsync[1],该算法中利用数据分块算法对需要同步的文件进行等长分块,然后通过分块比较得到两个文件间的差异数据。不过Rsync中使用的数据分块算法是固定长度的数据分块算法,这类算法存在字节漂移的问题:当在文件的起始位置插入一个字节,将会导致文件所有的分块发生变化。这种问题在定位差异数据时会导致发现的差异数据远大于实际变化的数据,虽然Rsync采用了别的方法规避了字节漂移,但却大大增加了算法的计算量。在Rsync的基础上,为了加快差异定位的速度,Lkhagvasuren Ider等人提出了一种两级分块策略[2],数据块大小分别为4 MB和32 KB。在第一级,使用4 MB块大小的索引表,采用字节索引分块的方法快速检测出大尺寸相同的数据块。在第二级,使用32 KB索引表对通过第一级文件相似性检测生成的整个非重复数据区域执行字节索引分块。

为了避免固定长度分块算法的字节漂移问题,学者们开始探索可变长度分块算法(Content-Defined Chunking,CDC)在差异数据定位中的应用。最早的可变长度分块算法基于Rabin指纹[3]的分块算法,该算法以匹配指纹为分块依据,增加了分块的抗字节漂移能力。Xia Wen等人为了追求分块速度,提出了FastCDC算法[4],在指纹匹配过程中使用Gear指纹代替Rabin指纹,并在窗口移动过程中使用一次移动两个字节的方式加快文件遍历速度,同时还使用两种指纹匹配难度增加了分块的稳定性。文章中,作者对FastCDC在单次匹配过程中成功的概率进行了简单的介绍,并讨论了跨字节时匹配概率的变化,但没有推敲算法设计上的优劣。为了减少指纹匹配存在的较大计算量,Bjrner Nikolaj等人提出了基于区间最大值的分块算法LMC[5],通过寻找一个固定窗口内的最大值是否在窗口的中间位置来判断是否设置切点,文中探讨了LMC算法在寻找切点时的概率问题,但同样没有讨论这个概率对差异定位的影响。除此之外,还有一些应用在重复数据删除[6-7]中的数据分块算法[8-11],这些算法的作者在论文中也有提及算法的分块效率、分块平均长度等,但都没有讨论数据分块算法各参数对差异数据定位的影响。

已有的研究中,学者们提出了很多数据分块算法以提升差异数据定位的效果,比如速度[12-13]、差异数据的大小[14-16]。但是这些研究是以实验数据为支撑,通过与已有算法做比较,得到实验上的优势,然后证明所提算法的先进性。通过实验的手段来验证算法的先进性会因为实验数据或算法参数的不同而产生偏差,且没有去探讨借助数据分块算法来定位差异数据的正确性,比如能否定位到所有的不一样的数据。此外,定位到的差异数据大小与数据分块算法存在什么关系,怎样设计数据分块算法才能在包含所有不一样的数据的前提下尽可能地减少定位到的差异数据,这些问题也是现有研究中的空缺。因此,为了解决这些问题,该文将数据分块算法抽象成一种窗口的模式匹配过程,并在此基础上证明了借助数据分块算法来定位差异数据的正确性,同时给出了定位到差异数据大小与数据分块算法的关系,为后人在设计数据分块算法时提供参考。

2 准备知识

本节对差异数据定位的详细过程进行阐述,并将这一过程中涉及到的对象进行符号定义以便后文讨论。同时,对数据分块算法进行了抽象,并对其中涉及到的参数等进行了符号定义,以方便后文的讨论。

在定位差异数据时,使用数据分块算法对data1和data2进行分块。数据分块算法的目的是对数据进行分块,分块的依据是在数据中寻找切点,相邻两个切点之间的数据就属于一个分块。数据分块算法可以分为固定长度分块和基于内容的数据分块。固定长度分块由于存在字节漂移的问题,在定位差异数据时一般不采用。基于内容的数据分块算法(Content-Defined Chunking,CDC)是在待分块数据中寻找符合特定条件的数据窗口,首先从数据的第一个字节开始,选取窗口大小的相邻数据,如果符合特定条件,则在该数据窗口的最后一个字节处设置切点,然后从下一个字节开始选取窗口大小的相邻数据,继续寻找切点。如果不符合,则将窗口往后移动一个字节,继续判断,直至找到符合特定条件的窗口或者数据结束。

该文将寻找符合特定条件的数据窗口的过程抽象为基于固定长度窗口的模式匹配,并记模式匹配成功的概率记为θ1。在对已有数据分块算法的研究中发现,大多数数据分块算法寻找切点的方式符合该抽象模型。在对以往CDC的分析中得到一个有趣的结论,即对于一个给定的CDC,在一次随机匹配的过程中,θ为一个可计算的固定值。此外,相邻窗口匹配成功的概率是不相互独立的,这是因为在进行模式匹配的过程中是采取逐字节移动的方式,因此相邻窗口间会存在数据的重叠,如图2所示。由于Window1,Window2之间存在重叠的数据,Window1匹配成功有可能增加Window2匹配成功的概率,反之亦然。但是为了更加客观地对待匹配的随机性同时降低推导的难度,该文假定所有窗口进行模式匹配时成功或失败是相互独立的。

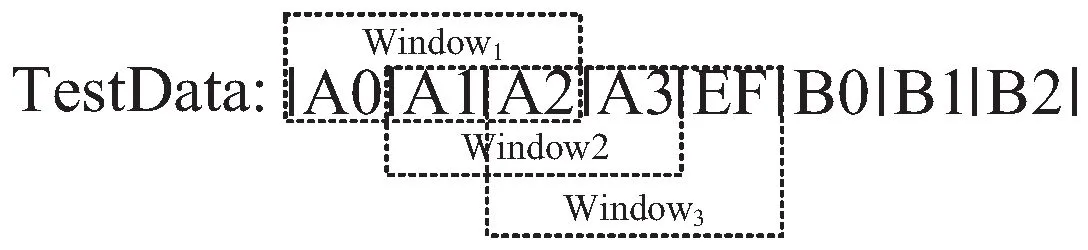
图2 重叠窗口的情况

基于固定长度窗口的模式匹配过程如图3所示。对于窗口(图3中的Window)内的数据,如果满足预先设计的匹配规则,则视为匹配成功,反之匹配失败。需要注意的是,匹配成功并不一定会在窗口处形成分块的切点,比如图3中,假设Window1处形成了一个切点,那么即使Window2可以匹配成功也不会产生切点,这是因为下一次的模式匹配是从字节A3开始的。

图3 基于固定长度窗口的模式匹配过程

为了方便后文的讨论,对用到的一些对象或者名称进行符号定义。

data1:定位差异数据时的原数据。

data2:定位差异数据时,在data1的基础上修改之后得到的数据。

n:模式匹配窗口的长度。

θ:一个随机窗口进行模式匹配时成功的概率。

FW(Fit Window):模式匹配成功且形成切点的数据窗口。

3 差异数据定位正确性与数据分块算法的关系

本节讨论借助数据分块算法来定位差异数据时的正确性。通过给出一些定义,并借助定义来推导差异数据定位的正确性。

定义1:字节数据是一个集合,集合中的元素满足条件:由1个或多个字节按照特定顺序拼接而成数据。字节数据记作B。对于b∈B,b中的每个字节byte,记作byteb。

在存储领域,任意一个数据均可以视为B的一个元素。如果将完全相同的两个数据视为一个,那么数据与B中元素是一一对应的关系。对存储在磁盘上的数据进行处理时,默认不会发生磁盘故障。基于这一点,在讨论的过程中,对于发生概率小于磁盘故障概率的事件,视为不会发生。

定义2:<=>,表示B上的一个二元关系。对于∀b1,b2∈B,当满足b1与b2相同时,记作b1<=>b2,反之记作b1<≠>b2。

引理1:对于∀b1,b2∈B,如果b1与b2不同的概率p<θ,其中θ表示磁盘损坏的概率,则b1<≠>b2。

证明:因对存储在磁盘上的数据进行讨论时,发生概率小于θ的事件视为不会发生,因此依然存在b1与b2相同,即b1<=>b2。

定义3:对于∀b∈B,如果存在B上的一个映射关系f,使得唯一存在∀b'∈B,且f(b)<=>b',则称f为B的一个属性,f(b)为b在该属性上的值。

定义4:对于∀b1,b2∈B,f为B的一个属性,如果f(b1)<=>f(b2)→b1<=>b2,则称f为B的可信属性。

引理2:对于∀b1,b2∈B,f为B的一个可信属性,则f(b1)<≠>f(b2)→b1<≠>b2。

证明:反证法,假设存在b1<≠>b2∧f(b1)<=>f(b2),这与可信属性的定义矛盾,引理得证。

引理3:MD5哈希是B的可信属性。

证明:对于∀b∈B,其MD5哈希存在唯一性,即MD5哈希是B的一个属性。对于MD5相同的两个数据,它们不同的概率低于磁盘故障的概率,由引理1及可信属性的定义可知,MD5哈希为B的可信属性。引理得证。

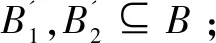
由定理1可知,对于存在于data1中的字节,如果不存在于data2中,则一定会被检测到。不过,在实际应用中,单检测出差异的字节是不够的,还需要根据data1和BD来得到data2。

定理2:对于∀data1,data2∈B,设它们之间的差异数据为BD,若data1的分块集合为B1,data2的分块集合为B2,则B2=B1+BD。

证明:反证法,假设∃b,s.tb∈B2&b∉B1&b∉BD。由于b∈B2&b∉B1,由差异数据的定位过程可知b∈BD,这与假设相矛盾,定理得证。

由定理2可知,B2中所有分块均可以从B1或BD的分块中获得。因此,借助数据分块算法来实现差异数据定位时,只需要记录B2中分块在B1或BD中对应的分块,就可以在B1所在的节点,结合BD来拼接出B2。这就意味着,当B1和B2不在同一节点上时,B1只需要BD就可以得到B2的内容,进而可以实现增量同步等目的。

综合以上讨论,使用数据分块算法来实现差异数据定位不仅可以保证差异数据中包含了所有的变化数据,还可以借助data1和差异数据来获得data2。

4 差异数据大小与数据分块算法的关系

在理想的情况下,差异数据的大小理论上应当与实际的修改量相同。当使用数据分块算法来定位差异数据时,由于最小单位是分块,而不是字节,因此定位出的差异数据往往比实际修改量大。为此,该文将对实际得到的差异数据大小进行讨论。

如上文所说,data2是在data1的基础上修改得到的,那么寻找data2和data1之间的差异数据实际上就是寻找在对data1的一次修改后受影响的分块。数据的修改一般包括三种:增加、删除和变动。数据的修改量也可以有很多种情况,该文首先以单个字节的变动为例来讨论受影响的分块。假设data1的分块结果如图4所示。其中FWi表示匹配成功的窗口。设模式匹配窗口的长度为n,模式匹配成功的概率为θ,data1为无边界的一段数据,其长度为L。

图4 data1的分块结果

当单个字节变动发生后,会有两种情况发生:一种是包含该字节的某个窗口形成了FW,另一种是包含该字节的所有窗口都没有形成FW。如果要data1在字节变动后受影响的分块,就必须找到受影响的FWi。如果原来的FWi所在的窗口依然是FW,那么受影响的分块就是字节变动所在的分块。如果原来的FWi所在的窗口不再是FW,那么受影响的分块就是FWi所在的分块以及相邻的下一个分块,小概率影响更多后续分块(FWi之间距离较近的情况)。接下来,在这两种情况下分别讨论对FWi的影响。在讨论之前,需要有一个假设:不存在两个满足匹配条件的窗口有重叠区域,否则会产生严重的字节漂移问题。

当包含该字节的某个窗口形成了FW时(只会有一个窗口形成FW),会有两种情况使得原来的FWi依然是FW:一是原来的FWi在新形成的FW之前或两者不存在重叠区域,一种是原来的FWi与新形成的FW完全重叠。当原来的FWi在新形成的FW之前时,即使存在重叠区域,也会将新形成的FW破坏掉。设包含该字节的某个窗口形成了FW时,原来的FWi依然是FW的概率为P1,则:

P1=(1-θ)n-1

(1)

设包含该字节的某个窗口形成了FW的概率为P2,则:

P2=1-(1-θ)n

(2)

当包含该字节的所有窗口都没有形成FW时,概率记为P3。会有一种情况使得原来的FWi依然是FW:该字节不在FWi中。设包含该字节的所有窗口都没有形成FW时,原来的FWi依然是FW的概率为P4。则:

P3=1-P2

(3)

P4=(1-θ)n

(4)

设一次字节变动所引起的差异数据为,则可以得出公式(5)。

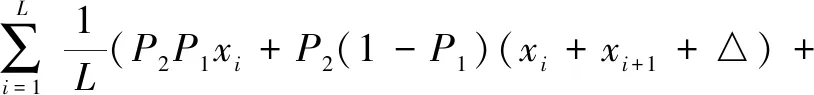
P3P4xi+P3(1-P4)(xi+xi+1+▽))

(5)

N=P2*2E(xi)-P2P1E(xi)+P3*2E(xi)-

P3P4E(xi)+▽

(6)

(1-θ)n-1+▽)

(7)

n-1)(2θ(1-θ)2n-1ln(1-θ)-

(1-θ)n-1ln(1-θ))

(8)

θ-1-θ+1+▽

(9)

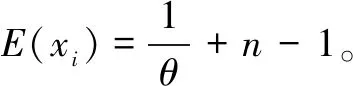
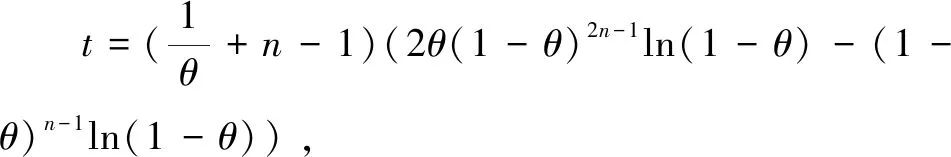
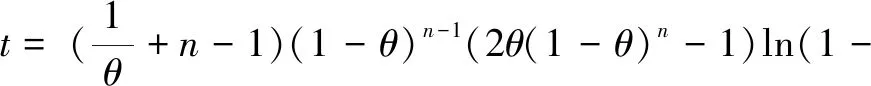
在定位差异数据时,上文已经证明差异数据中包含了所有变动数据,那么为了取得更好的定位效果,只需要降低差异数据的大小,即让N尽可能小。既然N与n是正相关的,且n为正整数,那么令n=1,代入公式(7)得到公式(9)。

理论上,根据公式(7)可以推导出N与θ的关系,但是经过较长时间的工作之后始终未能得出一个有效的结果。在后续的研究中将继续努力,以期可以得出N与θ的具体关系。

综上所述,在原数据只发生单个字节变动时,借助数据分块算法定位得到的差异数据的大小与数据分块算法的匹配窗口大小正相关。当匹配窗口大小为1时,差异数据的大小与窗口匹配成功的概率负相关。该结论可以通过图5形象地说明,图中C1和C3是分块中的非匹配窗口字段,C2和C4是匹配窗口字段,深色背景表示因字节变动产生的差异数据。由上文的分析可知,在θ相同的情况下,C1长度与匹配窗口的长度无关,因此在图5(b)场景下,差异定位的长度与匹配窗口的长度正相关。同理,在图5(c)场景下,差异定位的长度与匹配窗口的长度也是正相关。

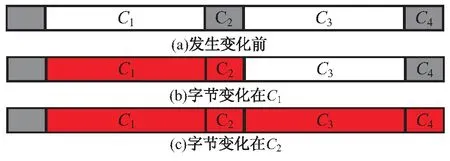
图5 差异数据的大小与算法匹配窗口大小的关系

当原数据发生单个字节的增加或删除时,可以理解为双字节变成了单字节,或单字节变成了双字节,进而也可以得出类似的结论。对于多个字节发生变化的情况,可以理解成发生了多次单字节变化,进而也同样可以得出类似的结论。

因此可以得出结论:当原数据发生变化时,借助数据分块算法定位得到的差异数据的大小与数据分块算法的匹配窗口大小成正比。当匹配窗口大小为1时,差异数据的大小与窗口匹配成功的概率成反比。另外,当匹配窗口大小不为1时,需要从公式(7)中计算此时N与θ的关系。

需要注意的是,在实际使用中,当n固定时,θ的值是无法取到任意值的,因为一个匹配窗口内的数据的可能性是有一定范围的。比如,一个长度为1的匹配窗口,那么窗口中数据的种类最多只有256种,无法依据这256种可能来设计任意的匹配概率。此外,当差异数据定位用在数据增量同步等场景时,对数据分块的数量有要求,分块数量的增多会产生更多的网络带宽。因此在定位差异数据时,并不是θ越大越好,应该先根据分块数量计算出大致的θ值,然后找出满足θ的最小n值,然后利用公式(7)来寻找最优的θ,进而设计出一个较优的数据分块算法。

5 结束语

首先对借助数据分块算法来定位差异数据的过程进行抽象,利用数据集合的相关理论证明了这一过程的正确性,其中包括定位到的差异数据包含了所有的变化数据,原数据借助差异数据的帮助可以拼接得到变化后的数据。然后,将数据分块算法抽象为一种基于固定长度窗口的模式匹配过程,通过推导的方式得出了数据分块算法中窗口大小和匹配成功概率两个参数与定位得到的差异数据大小之间的关系。并得出数据分块算法的窗口大小参数与定位得到的差异数据大小成正比,匹配成功概率参数在窗口大小为1的情况下与定位得到的差异数据大小成反比。这对设计数据分块算法有一定的参考意义。

不过,该文未能给出一个差异数据大小与匹配成功的概率之间具体的关系,此外N与θ的关系也未能给出一个准确的结论,有待进一步研究。