面向电网工程的智能数据采集与分析验收方法研究
2023-10-21鲍海泉方瑞寅
鲍海泉,方瑞寅
(国网湖北省电力有限公司襄阳供电公司,湖北襄阳 441000)
近年来随着电力行业数字化转型的推进,信息技术在电力工程的设计、施工及验收流程中均具有更加深入的应用[1-4]。根据电网公司数字化应用与建设的要求,在电力工程建设中,应实现建设过程的“所见即所得”,深化减负增效。以电力工程的随工验收为例:1)工程的进度不直观、不准确,需要验收人员进行现场查看;2)现场施工工艺的验收仍依赖于传统人工测量,验收单的填写通常需要手动计算后再录入,由此便造成了人工、时间成本的提升,故需在数字化转型的过程中加以改进[5-8]。现阶段通过部署智能化的实测实量设备,实现数字化管控施工计划并精准把控施工进度是提升验收效率的有效方法,也是电力工程验收的发展方向[9-12]。
基于上述背景,该文对智能化验收中的数据采集与分析方法展开了研究。通过现场的激光扫描设备及验收表单赋予电网信息模型(Grid Information Model,GIM),以三维模型直观展示实测实量数据,并准确标记存在问题的位置,从而帮助管理人员准确获取项目进度。文中对三维激光扫描技术的可视化流程进行了分析,且对数据的处理方法加以改进。此外还根据获取数据的稀疏性,提出了具体的分析方法,进而提升了数据建模的效率。
1 理论设计
1.1 三维激光扫描
为实现电网验收全流程的可视化,该文借助激光扫描技术对变电站中的各物体进行了三维激光扫描,以获取三维点云数据[13-14],并实现了三维图像的建模,具体流程如图1 所示。

图1 三维数据采集与建模流程
在数学上,点云数据包括欧式距离(Euclidean Distance)、法向量与曲率等信息。但由于激光扫描过程中所获得的点云数据内部无几何分布,导致数据集呈离散状态。因此,需要先建立点云数据点间的空间拓扑关系,再实现计算机的硬件存储。点云数据的法向量是建立空间拓扑关系的关键,该文基于最小二乘法(Least Sqaure Method)实现了法向量的估计[15-17]。
以式(2)为切片Sj所属平面在三维空间内拟合后的平面方程,δ为切片最大值,式(3)为该平面方程的法向量,记,根据最小二乘法对式(2)进行拟合,则拟合误差为:
整理式(4)和式(5),通过矩阵的形式进行求解可得:
经过上述流程,可得到具有二义性的法向量。在具体建模过程中,不同数值会导致法向量的朝向也有所不同,从而使得三维模型产生视觉差异。因此,还需对法向量的朝向进行规则化处理。
具体方法如下:对于N个采样点构成的点云模型,记Si为其K邻域,为其质心,首先将质心变换至坐标原点,则有:
随后,将法向量分别绕x、y轴旋转,即可将法向量置成与z轴同向:
其中,α、β分别为x、y方向的旋转角度,定义B、C分别为向量在xoz、yoz平面内的投影,则:
1.2 点云数据的压缩与重建
通常情况下,电力工程建设现场激光扫描设备所获取的点云数据均是超量且稀疏的。若直接进行三维建模,则会浪费计算资源,从而影响建模效率,故需利用采集的稀疏性对点云数据进行精简压缩。该文在压缩时基于全变分(Total Variation,TV)模型理论,具体方法如下:通过k-近邻(k-NN)算法先将原始采集信息划分为M个切片。此时S是一个K行M列矩阵,记D为R域上的L维过完备字典ϕ的过渡矩阵,则可得到对应的等效转化关系为:
记原始采集的维度为N,精简后的维度为W,此时式(11)可转化为欠定方程的求解问题。根据L1范数的性质,将原始信号u的重建转化为L1范数最小化,如式(12)所示:
但若仅依靠L1范数,无法消除重构模型时信号的稀疏性影响。此时可以借助信号中的梯度稀疏性,采用TV 模型进行等效计算,如式(13)所示:
同时使用L1范数与TV 模型,便可融合二者优势,如式(14)所示:
其中,旋转角度α、β在式中分别为TV 模型与L1的调节因子。对于式(14),为保证其可达到信号重建的上界,再引入稀疏性约束:
式中,ψ-1为小波变换,A为R上的傅里叶变换。对于式(15)可采用多种优化方法进行求解。
2 方法实现
2.1 仿真实验设计
为评估算法的性能,该文使用斯坦福大学三维扫描数据库的开放数据集Bunny 与Dragon 来进行算法性能测试。这两个数据集的基本参数如表1所示。

表1 数据集参数
该次从简化程度、绘制精度及运行速度这三方面对改进后的算法性能加以评估。所对应的评估指标则分别为精简比率(Simplification Rate,SR)、均方根误 差(RMSE)、简化耗时(Simplification Time,ST)。其中,SR、RMSE 的指标定义方式分别如下所示:
式中,Nq为原始三维模型中的采样点个数,Nh则为算法精简后的采样点个数,Cq为三维模型的实际参数,Ch为精简模型插值后的参数值。
为了合理评估算法的运行耗时,文中使用表2的软硬件参数作为算法仿真环境。

表2 算法仿真的软硬件环境
2.2 仿真结果
在仿真时,以SR 为自变量,以RMSE 及算法运行耗时为因变量来对模型性能进行评估。此外,为评估模型性能的改善效果,还引入了随机降采样优化作为对照实验组。表3-6 分别为Bunny 数据集在SR 为60%、80%以及Dragon 数据集在SR 为80%、90%时,两种算法的三维建模效果。
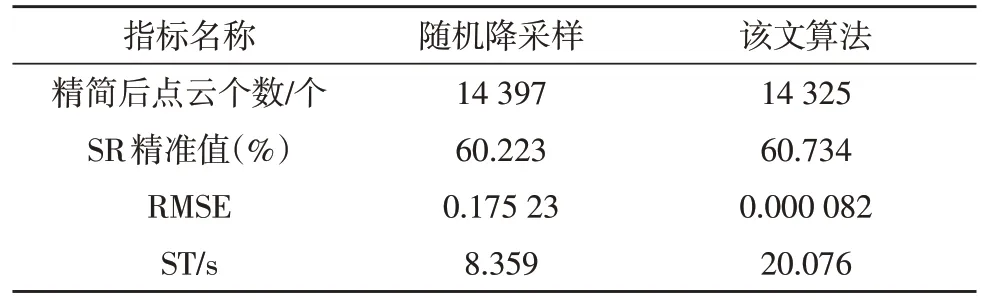
表3 Bunny数据集SR=60%时的三维建模效果
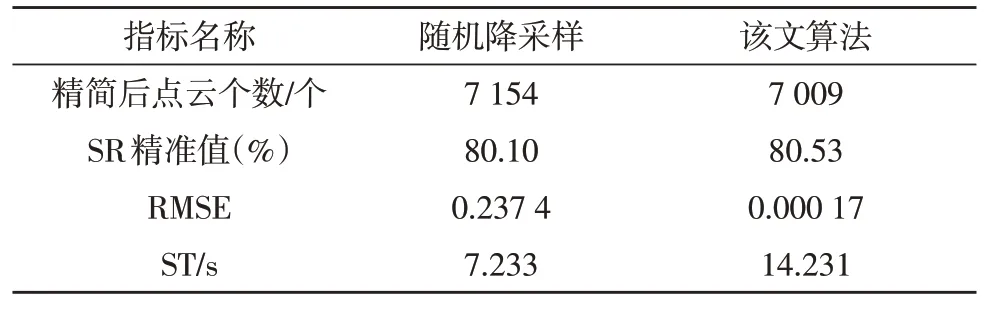
表4 Bunny数据集SR=80%时的三维建模效果

表5 Dragon数据集SR=80%时的三维建模效果
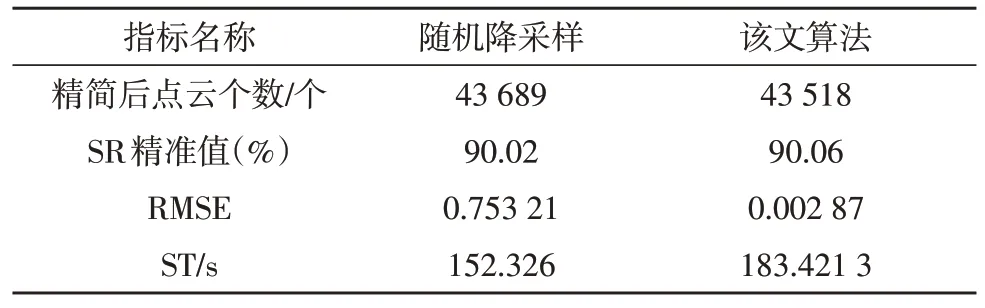
表6 Dragon数据集SR=90%时的三维建模效果
从点云数据集的规模看,Dragon 模型约为Bunny模型的10 倍,因此两个数据集分别可以评估该算法在大小规模数据集上的精简效果。整体来看,该算法在RMSE 精度上较随机降采样算法具有显著的提升。以Bunny 数据集SR=60%为例,精简后的RMSE达到了0.000 082。这表明数据精简后,建模效果几乎未发生改变。而在Dragon 数据集下,即使精简率提升到90%,该算法的RMSE 也能达到10×10-3的数量级。然而,所提算法在小规模数据集上的运行耗时(ST)上较随机降采样算法有较大劣势,如在Bunny数据集SR=60%时,该算法的ST 是其2.402 倍。但随着数据集规模的增长以及SR 的提升,所提算法的运行耗时与随机降采样算法的差距逐渐缩小。且当Dragon 数据集的SR=90%时,该算法的ST 是其的1.204 倍,这说明该算法在大规模数据集上的应用效率更高。
2.3 电网工程验收过程可视化仿真
在评估完算法性能后,该文在部署了数字工地平台的某变电站工程实际验收现场进行了三维建模仿真。经现场激光采集扫描后的点云数据以.PCD和.PLY 文件的格式进行存储。这两种格式文件的采集信息分别如表7-8 所示。
表7 .PCD文件内的采集信息
通过现场扫描,共获取567 824 个数据点,且数据规模与Dragon 相似。该次采用80%的精简率进行三维建模,具体建模效果如图2 所示。此时,相关的建模指标具体如表9 所示。
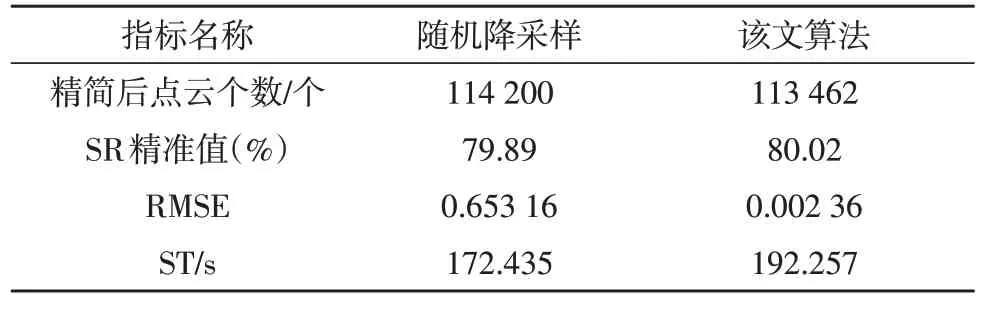
表9 某变电工程现场SR=80%时的三维建模效果

图2 变电工程现场建模效果
在仿真时,文中首先使用全量的点云数据进行建模测试,得到ST 为2 045.998 s。而利用该文算法进行精简后,建模时间降低了90.603%。对比随机降采样算法,该文算法的RMSE 可达到0.002 36,而时间成本仅提升了11.495%。
3 结束语
该文使用最小二乘法对建立工程现场采集的激光点云数据进行规则化处理,保证了三维建模时空间拓扑关系的完整性。同时,针对现场采集数据的稀疏特性,文中还对现场采集数据加以精简,在保证建模精度的同时提升了三维建模的效率。此外,随着电网数字化转型的加速,文中的理论与方法将会有更广阔的应用前景。
