基于北斗双重差分的输电线路杆塔位移分析方法
2023-10-21唐冬来宋卫平刘秋辉叶鸿飞
唐冬来,宋卫平,杨 梅,刘秋辉,黄 璞,叶鸿飞
(1.四川中电启明星信息技术有限公司,四川成都 610041;2.四川思极科技有限公司,四川成都 610047)
中国西南地区输电线路地理分布广泛,所处区域地貌特征多样[1-2],地质灾害类型多,极易导致输电线路杆塔发生倾斜和沉降[3],给输电线路带来了严重的安全隐患[4-5]。
许多学者对输电线路杆塔位移监测进行了研究,文献[6-7]通过罗德里格矩阵对轴加速度、杆塔角速度进行分析,以识别输电杆塔位移情况。文献[8]通过无人机搭载的激光雷达对输电杆塔位移进行激光扫描与分析。文献[9]通过YOLOv3 算法对比多张输电线路杆塔图片,从而分析杆塔的位移情况。但上述方法误差约为15 cm,不能满足精准监测需求。
针对输电杆塔位移监测难度大、精度低的问题,提出了基于北斗双重差分的输电杆塔位移分析方法。该方法在北斗卫星定位杆塔四角位置后,采用地面增强站的定位信息进行双重差分校准。
1 输电线路杆塔位移分析
基于北斗差分校准的输电线路杆塔位移分析框架分为北斗卫星杆塔定位、地基差分校准和杆塔位移识别三部分,其框架图如图1 所示。
在北斗卫星杆塔定位环节,首先,在输电线路杆塔的四角安装四套北斗监测终端,并将这四套终端与北斗卫星进行对时,确保北斗监测终端定位的准确性。其次,北斗监测终端进行卫星信号搜索,确保获取四个及以上北斗卫星的信号。再次,计算卫星发射到北斗监测终端接收到信号的时间差,测量北斗监测终端与四个北斗卫星的距离。最后,建立四颗北斗卫星之间的距离及北斗卫星到北斗监测终端的四元二次方程组,求解北斗监测终端的详细坐标。在地基差分校准环节,首先,利用三组以上的地基增强基准站持续观测北斗卫星,获得北斗卫星的位置数据。然后,计算单个地基增强基准站的卫星轨道误差、卫星钟差、对流层延迟等误差,最后,建立三个以上地基增强基准站网。利用地基增强基准站的观测数据计算输电线路杆塔的差分误差。在杆塔位移识别环节,首先,建立输电线路杆塔四个角的位置矩阵,并且每15 min 更新一次数据,将该数据和上一次的位置进行双重差分比较。当位置出现偏移时,进行输电线路杆塔位移预警。
2 输电线路杆塔位移分析模型
2.1 北斗卫星杆塔定位
2.1.1 北斗监测终端对时
输电线路杆塔一般为四角铁塔[10],为确保准确监测,在输电线路杆塔的四个基座上安装四套北斗监测终端。
终端时间是北斗监测终端距离测量的基础,北斗卫星的授时精度为10 ns[11],满足距离测量要求。在输电电缆杆塔卫星定位前,进行北斗监测终端的时钟对时,消除时钟不一致带来的北斗卫星定位误差影响。
四套北斗监测终端向北斗卫星请求下达的对时命令kc为:
式中,na为北斗监测终端的数量;k1,k2,…,kna为不同的北斗监测终端接收到北斗卫星的对时命令。
2.1.2 北斗卫星搜星
中国北斗3 号导航卫星由30 颗地球同步静止轨道卫星构成,在使用双频的模式下,高程精度达2.0 m[12]。中国的北斗卫星系统在空间中建立了一个全球卫星网络,在卫星轨道的分布设计下,地球上的任一个输电线路杆塔位置均能观测到四颗以上北斗卫星。而在同一时刻,北斗卫星在空间中的坐标系为固定的。输电线路杆塔北斗监测终端搜索星图如图2 所示。
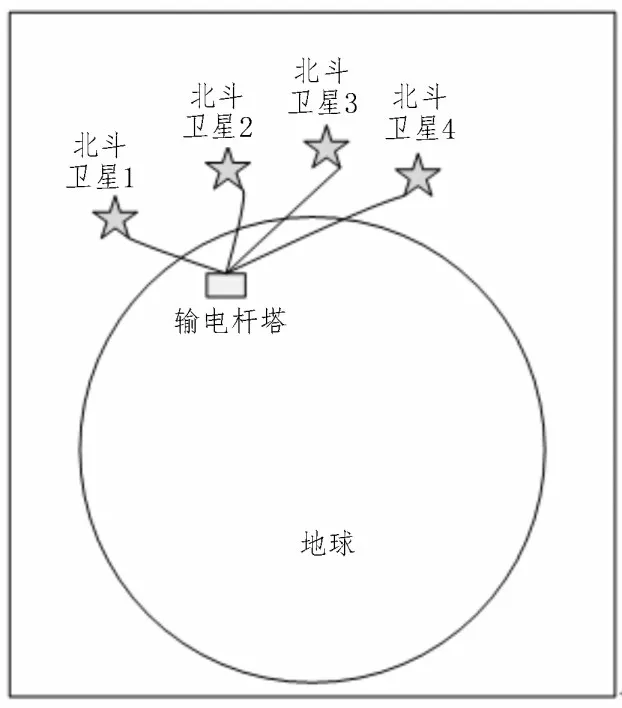
图2 输电线路杆塔北斗卫星搜星图
2.1.3 导航信号时间差计算
通过北斗对时后,在输电线路杆塔北斗监测终端和北斗卫星之间均有一个时钟一致的时刻表。这个时刻表即导航信号时间差计算的基础表。
输电线路杆塔北斗监测终端向北斗卫星请求定位指令后,北斗卫星下发带有时间戳的导航信号,输电线路杆塔北斗监测终端接收到导航信号后,记录接收时间。则利用发送与接收的时间差,乘上电磁波在空间中的传播速度,即可知道输电线路杆塔北斗监测终端到四颗卫星的距离la为:
式中,ta为北斗卫星下发导航信号的时间;tb为输电线路杆塔北斗监测终端接收到导航信号时间;sa为电磁波的传播速度。
2.1.4 输电线路杆塔位置定位
在已知输电线路杆塔监测装置与四颗北斗卫星的空间距离和输电线路杆塔监测装置到四颗北斗卫星的距离的情况下,建立四元二次方程组如下:
式中,xa、ya、za分别为输电线路杆塔监测装置的空间位置;xz1、yz1、zz1,xz2、yz2、zz2,xz3、yz3、zz3,xz4、yz4、zz4分别为四颗北斗卫星的空间位置;求解方程组即可获得输电线路杆塔监测装置的定位信息。
2.2 基地差分校准
2.2.1 地基增强站的北斗数据采集
通过北斗卫星导航定位输电线路杆塔位置的误差主要包括了卫星的日历误差、电粒子扰动时延误差等,导致北斗卫星的定位精度为2 m[13],此类精度的误差不能对输电线路杆塔的位移进行精准监测,因此,需加入地基增强站,以进行误差校准。首先,在输电线路附近的已知坐标点部署输电线路杆塔位移监测北斗地基增强基准站。然后,利用北斗地基增强基准站对北斗卫星进行持续观测,对卫星的空间坐标数据进行实时采集,则卫星的坐标历史数据Uz为:
式中,nb为北斗地基增强站采集的时间周期数量;ut1,ut2,…,utnb为不同的北斗地基增强站观测到北斗卫星的空间坐标。
2.2.2 单基站北斗误差测量
单输电线路杆塔北斗地基增强站的误差主要来源于卫星轨道误差、卫星钟差、对流层延迟等误差,其误差值hall为:
式中,ha、hb、hc分别为卫星轨道误差、卫星钟差、对流层延迟误差。
2.2.3 建立地基增强基准站网络及差分校准
为避免单基站北斗误差修正不足的问题,采用三个以上输电线路杆塔北斗地基增强基准站组成输电线路杆塔北斗地基增强基准站网,利用无线网络将输电线路杆塔北斗地基增强基准站的卫星坐标数据发送至输电线路杆塔位移数据处理系统中,数据处理系统根据地基增强基准站网络的北斗观测卫星数据计算出输电线路区域内部的差分修正值,并批量发送给输电线路杆塔北斗监测终端,从而计算出输电线路杆塔高精度的坐标位置数据。实现输电线路杆塔定位的大幅提升。
2.3 杆塔位移识别
杆塔位移识别是利用安装在输电线路杆塔塔基四个角的北斗监测终端观测数据进行差分综合识别。
双重差分法(Difference In Differences,DID)是一种数学微分方程法,通过随机分配的输电线路杆塔坐标的差分来近似导数,从而求解微分方程的近似值[14-15]。因此,文中采用该方法对输电线路杆塔四个角的坐标数据进行综合判断,从而识别输电线路杆塔的位移情况。双重差分输电线路杆塔位移识别的回归系数Ra为:
式中,ψ(j)为每15 min 更新一次坐标数据的输电线路杆塔四个角的位置数据;βt为差分干预后的输电线路杆塔位移自然增长量;Q为差分干预后带来的增量;s(j)为指示函数。
3 算例分析
3.1 场景与参数设定
采用文中所提基于北斗双重差分的输电线路杆塔位移分析方法在中国西南某输电线路杆塔进行现场应用。在地质灾害频发地区的输电线路安装了704 套北斗监测终端。且每个北斗监测终端均能接收到四颗及以上北斗卫星信号。北斗监测终端时钟同步的精度为10 ns,电磁波传播的速度为300 m/μs。
文中所提方法后台配置北斗卫星数据解算服务器,服务器的处理器为INTEL XEON W2223,核心频率为3.6 GHz,4 核心,8 线程。服务器内存为64 GB,硬盘容量为10 TB,服务器的计算机操作系统为Windows Server 2019。
文中用于比对的方法为文献[16]中的模态参数输电线路杆塔位移识别方法,该方法在输电线路杆塔位移识别中被广泛应用,具有识别精度高、速度快的特点。
3.2 算例运行分析
3.2.1 北斗授时精度分析
输电线路杆塔位移监测终端的时钟精度是衡量量测装置的核心指标,该指标越小,位移量测的误差就越小。该指标的计算方法:采用卫星或载波对输电线路杆塔位移监测终端进行授时,并将终端的时间与基准的时钟源进行比较,两者之间的时间差即为授时精度。
分别选择10、20、50、80、100、200、500、600 个位移监测终端,其中,文中所提方法采用了北斗监测终端,模态参数方法采用了载波授时的传感器。采用时钟源分别对其进行授时,其平均授时精度如表1所示。
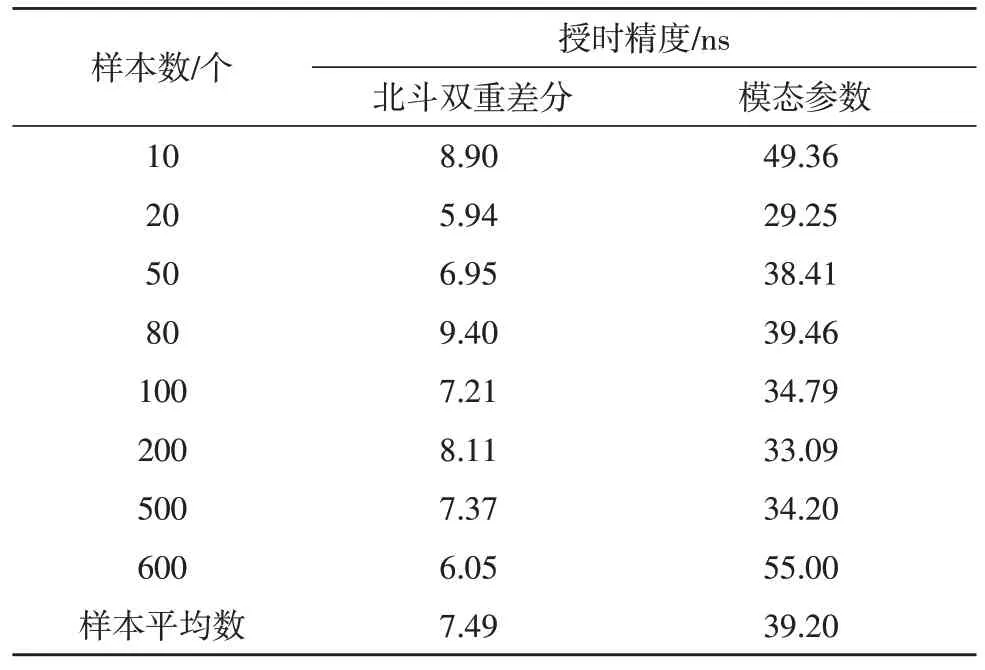
表1 北斗授时精度
由表1 可见,文中所提基于北斗双重差分的输电线路杆塔位移分析方法平均授时精度为7.49 ns,小于模态参数的载波授时方法平均精度39.2 ns,因此,文中所提方法授时精度更高[17-18]。
3.2.2 输电线路杆塔位移识别准确率分析
在输电线路杆塔因地质灾害发生位移后,需及时准确地通知输电运检人员。因此,位移识别准确率是衡量输电线路杆塔位移的核心指标。该指标的计算方法:输电运维人员将位移监测终端移动5 mm,观测输电线路杆塔位移监测系统中是否显示输电线路杆塔位移,若输电线路杆塔位移监测系统显示发生位移,则为识别准确,其比值为位移识别准确率。
选择移动输电线路杆塔位移监测终端个数为500、800、1 000、2 000、3 000、4 000,采用文中基于北斗双重差分的输电线路杆塔位移分析方法与模态参数法对比位移识别准确率,对比结果如图3 所示。

图3 输电线路杆塔位移识别准确率图
由图3 可见,文中基于北斗双重差分的输电线路杆塔位移分析方法平均输电线路杆塔位移识别准确率为99.1%,高于模态参数法的92.6%。
3.2.3 输电线路杆塔位移识别误差分析
输电线路杆塔位移识别误差分析是衡量输电线路杆塔位移分析度量值的核心指标,该指标越小,位移测量的误差就越小。该指标的计算方法:输电运维人员将位移监测终端移动35 mm,输电线路杆塔位移监测系统均监测到杆塔位移,观测输电线路杆塔位移监测系统中输电线路杆塔的位移值,两者之差即为输电线路杆塔位移识别误差。
选择移动输电线路杆塔位移监测终端个数为10、20、50、70、80、100、200、400,采用文中基于北斗双重差分的输电线路杆塔位移分析方法与模态参数法比较输电线路杆塔位移识别误差,比较结果如表2所示。

表2 输电线路杆塔位移识别误差
由表2 可见,文中基于北斗双重差分的输电线路杆塔位移分析方法平均位移识别误差为6.29 mm,低于模态参数法的22.76 mm。
4 结论
为解决输电线路杆塔位移监测难度大、精度低的问题,提出了一种基于北斗双重差分的输电线路杆塔位移分析方法。首先,该方法通过四颗以上北斗卫星进行杆塔初始定位;其次,采用地面增强站对杆塔位移信息进行差分校准,在此基础上,采用双重差分法对输电线路杆塔四个塔基的北斗位移监测终端紧张综合位移分析。最后,将该方法在某输电线路杆塔进行模拟试验,其结果验证了该方法的有效性。
