宽频信号在谐振接地有源配电网高阻故障选线中的应用
2023-10-21韦明杰王聪博
韦明杰,余 越,梁 英,王聪博,杨 帆
(1.电网安全全国重点实验室(中国电力科学研究院有限公司),北京市 100192;2.中国电力科学研究院有限公司,北京市 100192)
0 引言
配电网高阻故障多以导线断裂、坠地形成的接地故障为主[1],具有严重的人身安全和火灾隐患[2],需要将故障线路快速切除。但高阻故障过渡电阻可达数千欧以上[3-4],故障电流小、具有非线性特点,且特征规律受系统运行方式影响大,选线可靠性难保证。随着分布式电源渗透率的不断升高,其对故障零序网络的影响不宜再简单忽略,尤其是分布式电源的非线性运行会对故障原有的波形畸变和谐波分布等非线性特征产生影响,而两种非线性的耦合也为故障特征规律的分析带来挑战[5]。
传统暂态无功方向法[6]、稳态有功方向法[7]和行波法[8]是谐振接地系统接地故障选线较常见的几种技术路线,但应对高阻故障问题均存在一定局限。对于暂态法,高阻故障的阻尼效应使得故障暂态量的主谐振频率随着过渡电阻的增加而跌落至工频附近,不再具备传统无功分量的极性特点。文献[9]提出了暂态零序投影系数法,在原理上给出了暂态主谐振频率跌落后的选线特征量构建方法。但暂态法对故障初始阶段特征的依赖,使其在应用时依然无法有效解决高阻故障发生时刻的超高阻值给初始特征捕获和精确提取等带来的阻碍,行波法也有同样的问题。稳态有功方向法[10]须在中性点增设并联电阻以提高对弱信号的有功相位测量精度,除了中性点的改造成本问题,此类方法在间歇性接地等强非线性场景下不易保证工频相位的测量精度,也使其实际应用受限。
近年来,为克服以上方法的盲区,高阻故障的气隙电弧击穿等物理过程产生的非线性特征得到广泛研究,并应用于故障选线。故障非线性能够持续贯穿整个故障接地过程,其直接体现是波形的畸变[11-12]和信号的宽频化[13]。但目前对故障非线性特征描述的依据大多是对一定数量的实际故障波形形态的总结,而对故障非线性特征的内在机理、特征随系统运行方式和空间位置的变化规律等问题缺乏探讨,造成选线算法对故障过渡电阻水平、网络拓扑和中性点运行方式等场景差异的适应性不强。同时,分布式电源大规模接入使得配电网更易产生弱馈现象,其非线性运行方式对网侧零序信号的影响逐渐突出。上述方法仅基于对高阻故障非线性特征的简单总结使得其在分布式电源非线性干扰下的有效性将受到影响。
本文介绍了高阻故障介质击穿非线性的产生机理和频谱特性,推导了含分布式电源配电网发生非线性高阻故障时的宽频信号数学表达,提出能够适应分布式电源非线性状态和系统多变运行方式的高阻故障选线技术。通过仿真、实际故障案例测试以及与主流算法的对比验证了所提算法的优势。
1 含分布式电源配电网高阻故障宽频特征的主要影响因素
1.1 高阻故障介质击穿非线性
高阻故障主要包含两种介质击穿形式:导体与地面间气隙电弧击穿和对地面的固体介质击穿。
在气隙电弧击穿过程中,受电弧电流在穿越零点后的热惯性作用、游离和去游离的竞争作用,呈现出非线性的电压和电流关系轨迹,如附录A 图A1(a)所示[14-15],其中,电压和电流幅值写作标幺值形式并以周期内最大瞬时幅值作为基准。不同过渡电阻下,电流过零阶段的伏安特性基本相似,但随着电流进一步升高,受过渡电阻对电压不同程度的抬升,伏安特性产生了较大差异。
固体介质的击穿过程随着电场强度的上升分别由杂质离子和自由电子(碰撞电离、阴极发射产生)主导,伏安曲线也从近似线性逐渐发展呈指数关系,从而表现为非线性,如附录A 图A1(b)所示为某实测高阻故障伏安特性曲线[11]。固体介质击穿中,空间散热更快,电和热的能量传递速度差异减小、能量易平衡,热惯性小。因此,伏安特性曲线中靠近零点且斜率较大部分较平均地分布于一、四象限,与气隙电弧击穿伏安特性有明显差异。
目前,多数建模方法将高阻故障视作为两个击穿过程所等效非线性电阻的串联[16-17],但实际故障中的气隙电弧击穿会渗透于固体介质内部,其精细化建模更加复杂,但总体上均表现为信号波形有差异的畸变,在频谱上则是体现为不同形式的宽频化特点。图1 展示了某真型试验场中获取的38 组高阻故障电流在稳定阶段的频谱图,故障试验包含了草地、水泥、沙地、树枝等多种常见的高阻接地介质和干燥、浸水两种环境。受介质击穿特性影响,稳定的高阻故障电流包含大量低阶谐波,尤其以奇次分量为主导,但在不同场景下各谐波幅值乃至相位关系均随具体故障的非线性差异而变化。

图1 实测高阻故障的频谱特性Fig.1 Measured spectral characteristics of high-resistance faults
1.2 分布式电源非线性运行下的谐波注入
电力电子化的分布式电源及控制策略使其具有非线性特点,如基于脉冲整流器的逆变型光伏一般会产生6l±1(l=1,2,…)次谐波;低功率运行下的光伏还会向系统注入大量不对称的3 次和9 次谐波,含量可达5%以上[18]。在弱馈或分布式电源接入比例较高的配电网,上述谐波将对交流侧电网信号产生干扰。此外,配电网还接入有大量非线性负荷等谐波源,尤其是炼钢厂、锅炉厂等集中接入的大、中型非线性负荷用户,也会对网侧零序信号的波形、谐波幅值和相位等特征产生影响。
附录A 图A2 所示为在某10 kV 配电线路中开展高阻故障试验前后的不同位置零序电流,该线路末端因受周边大型化工厂和新能源产业基地影响,测量得到故障前的相电流和线电压的总谐波畸变率(total harmonic distortion,THD)分别达到了31.87%和3.28%。由于分布式电源并网变压器在网侧不接地,零序谐波电流不会直接注入网侧,而是通过对故障点电压的影响而叠加于零序网络故障支路的虚拟电势中[19]。分布式电源的非线性与高阻故障本身的非线性相耦合改变了故障原有的特征表现,也对故障信号分布规律的理论分析带来困扰。
2 谐振接地系统高阻故障宽频特征分析
2.1 高阻故障宽频信号表达式的建立
文献[20]从分布式参数模型出发,详细推导了谐振接地系统零序网络的等值方式。针对不同频率信号,各线路在对地电容、线路电感和中性点消弧线圈的谐振作用下,等效阻抗随着频率的升高对外交替表现为容性和感性。而在首容性频段内,每条线路的零序等效阻抗则可表示为对地电容和电阻的并联,如图2 所示。图中:C0i和R0i分别表示线路i的对地电容和对地电阻;L0N和R0N分别等于中性点对地等效并联电感和电阻数值的3 倍,其中,电阻反映的是消弧线圈内阻和阻尼电阻。
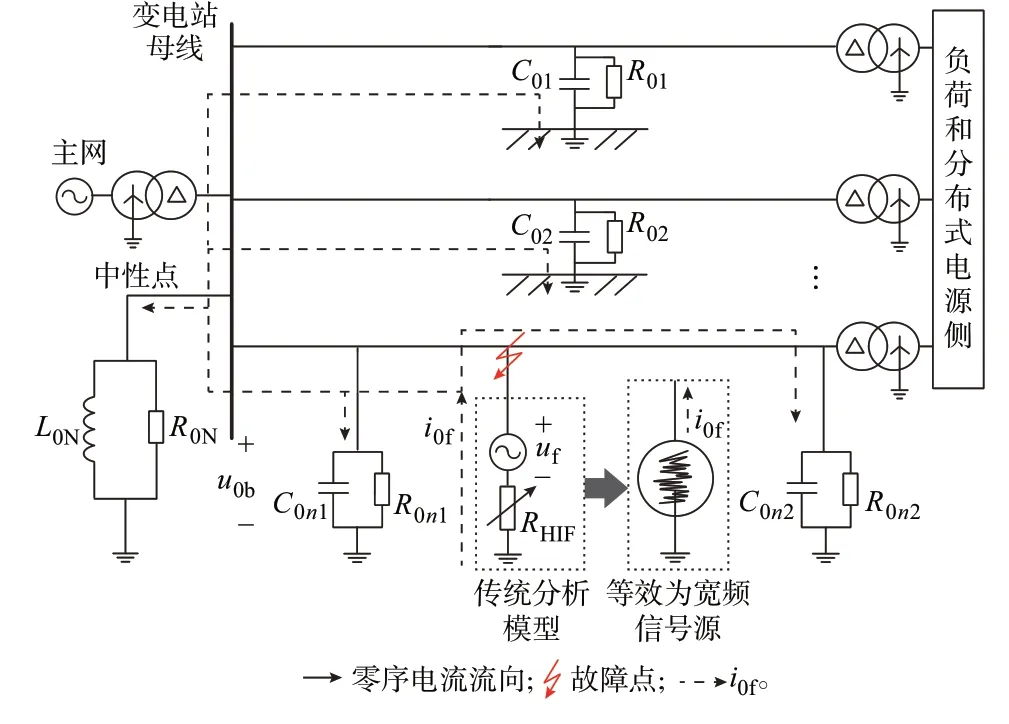
图2 n 出线有源配电网非线性系统的零序等效网络Fig.2 Zero-sequence equivalent network of active distribution network nonlinear system with n feeders
传统对高阻故障零序暂、稳态特征的分析,是在故障过渡电阻恒定的简化前提下,围绕工频虚拟电动势uf列写微分方程组,求解各点零序信号的解析表达式来实现[9]。但实际故障电阻和uf均为非线性,如前一章所述,分别反映了高阻介质本身的非线性以及分布式电源侧的非线性运行状态,需要探究此种耦合下的故障特征分析手段。
将图2 中的故障支路看作一个黑盒,不关注其内部电气量的转换关系,仅关注其外部特性。因此,可整体上等效为一个宽频信号源,记其端电压和输出电流瞬时信号分别为u0b和i0f。由此,高阻故障和分布式电源的非线性耦合将会反映在u0b和i0f之中。根据信号分析理论,在较短的时间窗口内,i0f可近似看作周期信号,可以写成不同频率正弦信号的叠加:

式(3)等号最右边为不含常数项的二阶非齐次微分方程,是线性运算,满足叠加特性。此外,将故障支路整体用一个宽频信号源等效后,图2 中除故障支路之外的零序网络为线性系统。将线性运算的叠加特性和线性系统不同频率信号传播的独立性[21-22]相结合,在式(3)代入各频率分量i0f,m的正弦表达式,可求解稳态时i0L0N的表达式如下:
在接地故障中,脱谐度(补偿度)v用来反映故障电流中消弧线圈感性分量对容性分量的补偿程度,系统阻尼率d则反映了阻性与容性分量的相对关系。传统意义上的脱谐度和阻尼率仅针对工频分量,本文所定义的vm和dm将上述变量的含义拓展至宽频,即vm表示故障电流中消弧线圈产生的感性m次谐波分量对容性分量的补偿程度,dm表示故障电流中阻性m次谐波分量与容性分量之比,其中:
这表明,在除故障支路外的线性系统中,消弧线圈的补偿和系统的阻尼效应对不同频率信号来说相互独立。
设故障发生于线路n,则健全线路零序电流i0i(i≠n)为该线路对地电容电流和电阻电流之和,故障线路i0n为健全线路和中性点对地电流之和的反向,以上各电流分量均可通过母线零序电压u0b建立与i0L0N的关系等式,并进而根据式(4)通过求解线性微分方程组分别获取i0i(i≠n)、i0n和u0b的表达式,最终均可写作如下形式:
从相量的角度,式(6)说明各条线路零序电流以及母线零序电压,均可以由故障点零序电流i0f的不同频率分量i0f,m在其各频率对应的相量平面分别旋转一定角度、乘以一定系数后的线性叠加而得。这里将所乘以的系数定义为幅值因子(factor),记为AFAC,m,将旋转的角度定义为相角因子,记为θFAC,m,它们的物理本质分别是幅值比和相角差。
通过求解线性微分方程组,可以求得i0i(i≠n)、i0n和u0b的幅值因子和相角因子的表达式如表1 所示,具体推导过程见附录B。特别地,线路i的零序电流相量和母线零序电压相量可写作:

表1 各信号不同频率分量相对于故障点电流的幅值和相角因子Table 1 Amplitude and phase factor of different frequency components of each signal relative to fault point current
式中:定义AFAC,m∠θFAC,m为电压、电流信号的m倍工频分量相对于故障电流对应分量的因子相量。
在表1 中,不同频率分量的各因子表达形式相似,但由于不同频率信号下各参数取值不同,相角因子可能相差π。例如,对于工频分量,-1
在零序网络中,故障电流i0f各频率分量的幅值和相角会随着高阻故障的非线性、阻值以及分布式电源的运行状态而变化。然而,由表1 可见,本文所给出的各因子表达式与上述因素无关,这表明不同零序信号、相同频率分量的幅值和相角之间的相对关系,对上述外界干扰因素是鲁棒的。这对本文后续构建故障特征量来解决分布式电源影响等问题有着重要的指导。
2.2 高阻故障宽频信号空间分布规律分析
对于谐振接地系统,消弧线圈的补偿使得零序工频信号,尤其是无功分量,在故障和健全线路中几乎没有差异,有功分量的差异也因配电系统不对称引起的“虚假有功分量”[23]和间歇性接地对相位测量的影响而可靠性受限。因此,本节重点探讨零序信号谐波分量的故障特征表现。
在表1 中,各参数含义明确,取值主要是由配电系统的结构和运行状态决定,遵循固有的标准和常理。消弧线圈理论上以轻微过补偿状态为宜,考虑实际中的调谐偏差,可设定v∈[-0.45,0.25];根据中性点阻尼电阻的一般水平,可设d∈[0.05,0.45];rR0i和ci分别为线路i的零序对地电导和电容在系统中的占比,设其范围为(0%,60%],其上限分别反映了线路绝缘较薄弱和线路为长电缆的可能场景。
根据表1 中公式,计算故障和健全线路零序电流因子相量AFAC,m∠θFAC,m随参数的变化规律,并以母线零序电压因子相量U̇FAC,0b,m的相角因子作为0°相位参考。图3 展示了2、3 次谐波的计算结果。
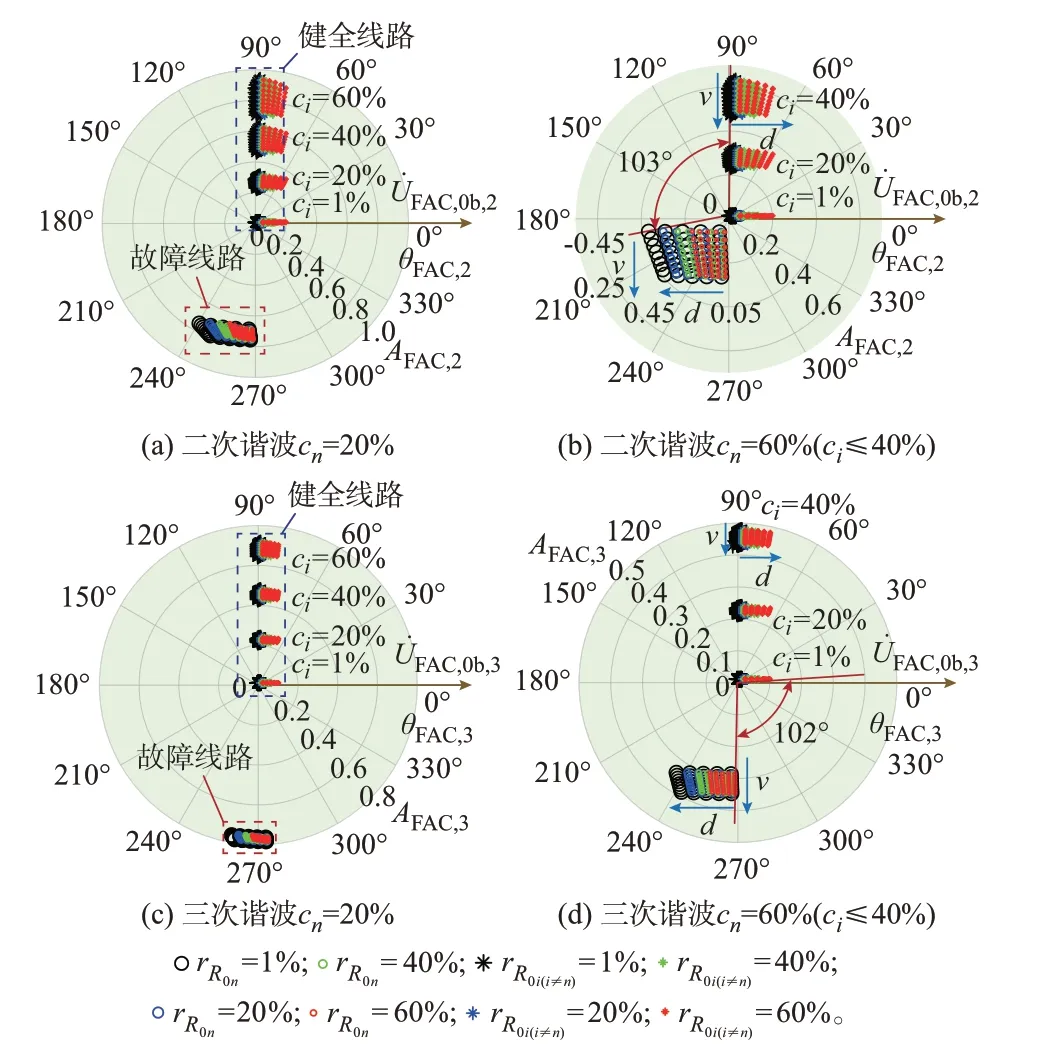
图3 2、3 次谐波因子相量的分布规律Fig.3 Distribution law of factor phasors of the second and third harmonics
不同参数的影响通过不同颜色、符号等形式来呈现。图3 表明,2 次和3 次谐波的因子相量已能够有效地区分出不同系统运行方式下的故障和健全线路,其中相角因子是体现差异的主要方面。总体上,健全线路谐波相量分布于超前电压0°~90°的区域,而故障线路则分布于超前电压180°~270°的区域。两者相角因子的差异由多个参数共同影响,其极小值Δθmin,m在对应频率的相量平面内达100°以上。根据表1 理论推导,Δθmin,m由2 次谐波开始随着频率的升高先减后增(如表2 所示)。考虑到现有新型配电网同步量测装置的守时精度一般在10 μs 以内[24],这对2 次谐波而言,引入的相位测量误差均不超过0.8°,对20 次谐波也不超过8°,足以满足故障和健全线路辨识的需求。
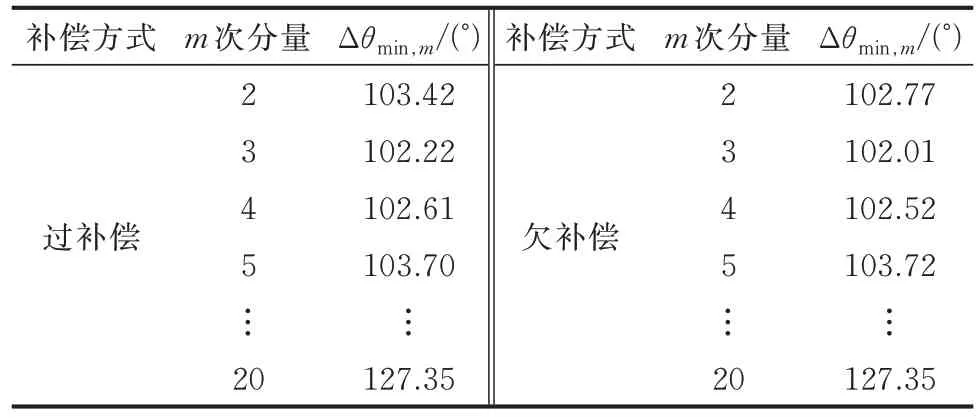
表2 健全和故障线路不同频率零序电流的最小相位差Table 2 The minimum phase difference of zerosequence current at different frequencies of healthy and faulty lines
由式(5)可知,当信号频率达到2 倍工频以上时,vm>0,即消弧线圈稳定地表现为欠补偿特性,这是使得上述频率分量下故障线路能够区别于健全线路,而不同于工频分量失效的根本原因。
进一步结合表1 可知,随着信号频率升高,公式中参数变化幅度减小,相角因子受系统运行方式的影响降低,故障和健全线路相角因子之间的差异增大。例如,1 000 Hz 分量,即20 次谐波(设其还处于首容性频段),vm≈1,dm≈0,代入表1 可知,故障和健全线路相角因子几乎完全相反,且不同运行方式下变化很小。然而,高阻故障阻尼效应极大地削弱了高频分量的幅值[9],尤其是在稳态时更可忽略不计。
综上所述,二次及以上的谐波分量相位对健全和故障线路具有区分能力,区分度随着频率的升高而增大,且对量测误差鲁棒。在信号含量方面,低阶奇次谐波分量较突出,并随频率升高而快速递减。因此,故障特征的描述方法应综合考虑低阶宽频分量,这更有利于借助非线性特征来实现高阻故障选线。
3 基于宽频同步测量的高阻故障选线
3.1 宽频特征量构建方法
据前文,可明确构建高阻故障选线特征量时的两个核心问题:1)多个零序信号的横向比较有助于提升对过渡电阻和分布式电源谐波干扰的鲁棒性;2)特征信号的选择应围绕零序低阶宽频谐波分量。
首先,多个零序信号的横向比较的方法主要包括是否使用零序电压两类思路。不使用零序电压时需利用多个出线零序电流进行横向对比,从而相互作为相位参考来构建反映极性差异的特征量,但对于高阻故障,可能存在相当一部分较短出线的零序电流幅值很小,从而与之横向对比所计算出的极性特征量均不准确,实际应用时不易处理、受限较大。因此,对于高阻故障选线问题,采集零序电压是必要的,可为所有出线零序电流提供统一、可靠的相位参考。
其次,宽频特征信号的选择有多种方式,下文主要讨论频段信号和离散频率信号这两种方式构建故障选线特征量的区别。结合图1,频段信号选为3~7 次谐波所涵盖范围,即Fb=[140,360] Hz,离散频率信号可有不同组合方式,本文仅以含量最高的3 次谐波为例来说明。根据上文分析,可知若利用零序电压和电流构建零序无功功率,健全线路各频率的零序无功为容性,而故障线路为感性,即两者极性相反。由此,记上述两种特征量分别为频段零序无功功率(特征量1)和3 次谐波零序无功功率(特征量2)。
对于特征量1,一个信号在某频段上的零序无功功率可采用瞬时无功功率来描述。记i0i和u0b在频段Fb上的分量分别为i0i,Fb和u0b,Fb,则对应的零序瞬时无功功率q0i,Fb表示如下:
式中:û0b,Fb为利用Hilbert 变换提取u0b,Fb在各频域上滞后90°后的信号,其中Hilbert 变换过程表现为一个幅频特性为1,正频率分量相移-90°的全通滤波器,是计算瞬时无功功率的经典手段之一[6]。
同理,特征量2 所对应的3 次谐波瞬时无功功率和周期无功功率可表示为:
式中:各变量对应的含义与特征量1 相同,仅是采用了不同下标来标记频率值。不难理解,q0i,Fb和q0i,3对于故障线路为正值,对于健全线路为负值。
3.2 特征量有效性评价及适用场景讨论
图4 分别展示了特征量1 和2 对某实测高阻故障特征的描述结果,其中线路2 为故障线路。
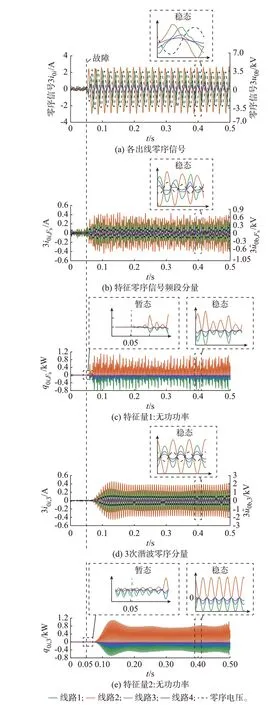
图4 3 kΩ 高阻故障特征量(经沥青接地)Fig.4 3 kΩ high-resistance fault feature (grounded through asphalts)
两种特征量的描述结果均符合理论预期,不论是û0b,Fb还 是û0b,3,在 极 性 上 都 表 现 出 与 故 障 线 路 零序电流总体相同、与健全线路零序电流总体相反的特点。另外,由于不同频率信号瞬时无功功率方向不完全同步,特征量1 中q0i,Fb的幅值总体略小于特征量2 中的q0i,3,即后者区分度略大。但在故障暂态阶段,因间谐波整体含量占比升高,而独立的离散频率信号含量占比显著降低,特征量1 所提取特征的区分度显著加强,尤其是在低阻故障时(如图5 所示)更为明显。
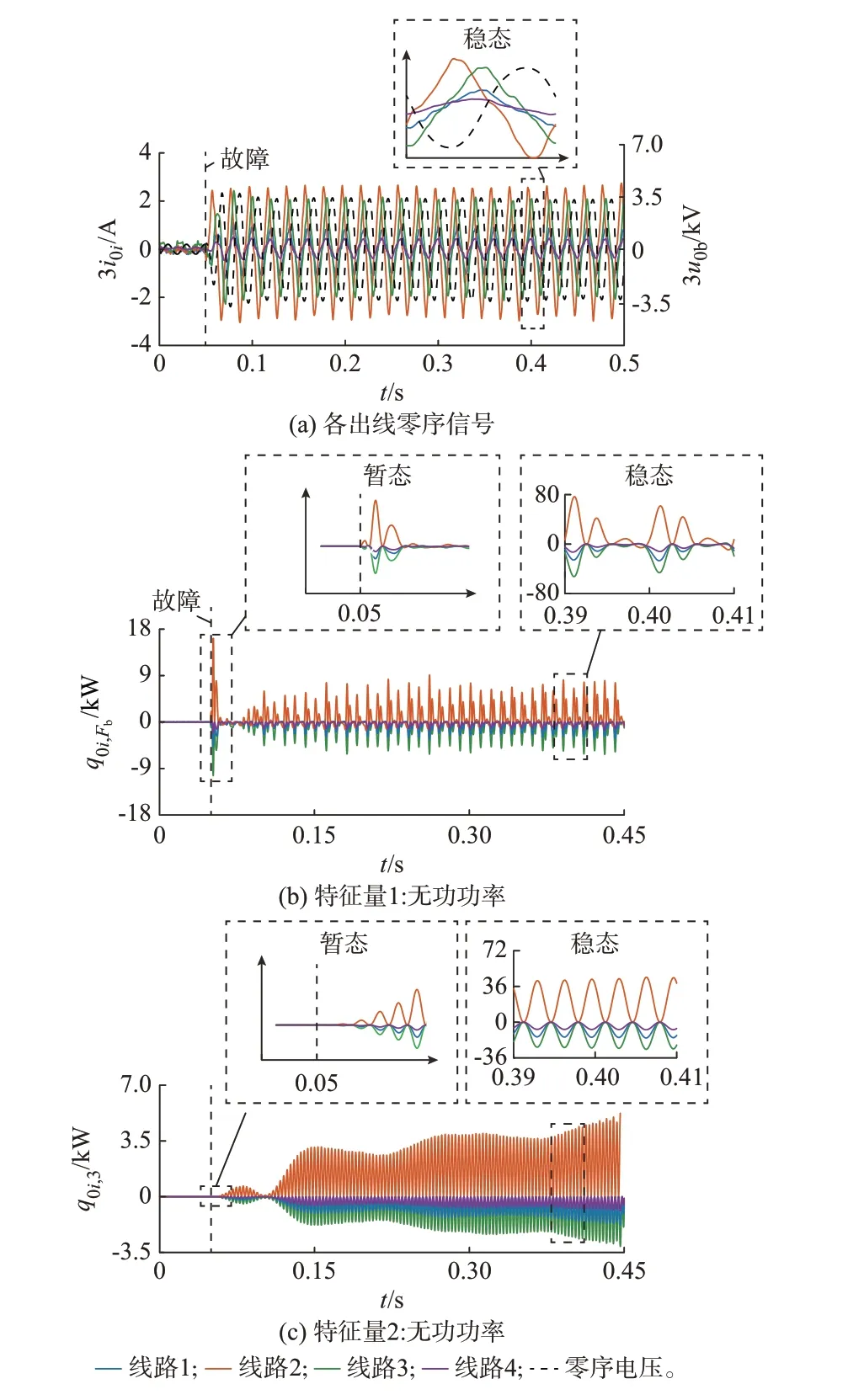
图5 0.7 kΩ 低阻故障特征量(经湿水泥接地)Fig.5 0.7 kΩ low-resistance fault feature (grounded through wet cement)
根据以上分析,特征量1 和2 是分别基于频段和离散频率信号所构建,两者各有优劣。在可靠性方面,特征量1 在保证较好的稳态特征提取能力的同时还能够有效地利用暂态阶段特征,特征量2 在稳态阶段的区分度略优,但提取暂态特征时劣势明显。在工程应用方面,特征量1 对连续频段特征值的计算需要获取零序电压和电流的高频采样信号,而特征量2 的计算实际上仅需获取特定频率的相量即可,对数据处理和通信传输要求小,更有利于拓展至广域和区域式保护。当然,若仅考虑本文所关注的故障选线问题,特征量1 对高频采样信号的需求可通过站内集中式采集和通信来实现,同时考虑其兼顾暂、稳态特征提取和故障选线的能力,故本文认为特征量1 更具有综合优势。
3.3 高阻故障选线判据
根据3.2 节讨论,设定线路i的频段零序无功功率特征量为Q0i,Fb,表达式为:
即为q0i,Fb所对应的在每个工频周期[t0,t0+T]中的平均无功功率。
需明确的是,高阻故障选线进程的启动建立在故障已被成功检测的前提下,其中后者由检测算法来实现,本文不对此赘述。故障选线流程如附录C图C1 所示,即从检测出的高阻故障发生时刻计起。若系统中存在某线路p,其Q0p,Fb满足式(11)中判据1,并同时满足判据2 中任一条件,则该线路为故障线路,并控制出线开关跳闸或上传告警信号。
式中:Kset为可靠性系数,当p为故障线路时判据1中不等号左侧应为无穷大(实际计算可将分母移至不等式右侧),不等式必然成立。当启动判据或故障检测判据误启动了选线流程,频段无功功率Q0i,Fb由正常状态下的零序信号计算而得,反映系统正常运行谐波和量测噪声,数值小且正负不定,具有随机性。对于出线数量大于3 的系统,判据1 不等号左侧数学期望不大于1.0。因此,可将Kset设定为3.0 并结合判据2 中的幅值和持续时长判据以规避误判,从而对选线启动判据的误启动具备一定的纠错能力。Q0p,Fb每周期计算一次,NY表示连续满足判据1的周期数。因此,判据2 是复合判据,当判据1 连续满足超过Nset个周期,或瞬时无功功率q0p,Fb超过定值qset,即判定线路p为故障线路。本文设Nset=10,qset=2 kW,分别从特征的持续时长或幅值水平对正常运行状态予以区分。
4 算例验证
4.1 算法可靠性分析
在图1 所述真型试验场中(包括2 个试验系统),在谐振接地方式下共测试高阻故障17 组,其中图4 和图5 通过两组案例具体展现了所构建特征量区分故障和健全线路非线性特征的能力和判据的有效性。表3 整理了17 组高阻故障实测案例的具体选线结果,不同故障因过渡电阻和非线性强弱有所不同。因此,无功功率特征量取值水平存在较大差异,但故障和健全线路的相反极性均能够清晰展现,从而式(11)判据1 不等号左侧取值为无穷大,所有高阻故障均能够正确可靠选线。

表3 10 kV 真型试验场实测高阻故障选线结果Table 3 Line selection results of high-resistance fault obtained in 10 kV experiment field
另外,为充分说明分布式电源非线性运行方式对算法的影响,在PSCAD 中搭建零序网络如图2 所示的配电网(设为3 出线系统),并令高阻故障发生于线路2 中部,采用非线性高阻故障模型[25]仿真得到典型故障零序电流波形、频段分量和选线特征量如图6(a)所示。随后,在线路3 末端连接一可控谐波源来灵活模拟分布式电源非线性运行下的谐波注入。参照文献[18]设置场景如下:注入谐波电流,在谐波源一侧测得3~9 阶奇次谐波含量分别为29.8%、12.1%、8.5%和2.1%。变压器的三角形接线无法完全滤除不对称的谐波分量,在线路3 末端测得相电压THD 超过15%,其中3 次谐波达9%,是实际中罕见的极端场景,由此来验证测试算法在极端谐波干扰下的鲁棒性。获取该场景下各线路首端零序电流、频段分量以及选线特征量如图6(b)所示。可见,在注入谐波影响下,各线路零序电流在频段内分量的幅值、相位均发生显著的波动,但频段内的电流和电压的极性关系未受影响(见图6(a)、(b)中间子图),健全和故障线路的特征量依然完全相反(见图6(a)、(b)下方子图)。这充分表明,所提出的选线方法利用非线性高阻故障产生的宽频特征,对分布式电源等非线性元件的谐波干扰具有良好的鲁棒性。

图6 非线性谐波源干扰下高阻故障特征Fig.6 Feature of high-resistance faults under nonlinear harmonic source interference
4.2 典型算法对比分析
现有多数高阻故障选线方法是对传统小电流接地故障选线技术的拓展,如在传统暂态功率方向法[6]基础上作改进的暂态零序投影系数法[9],利用中性点并联中电阻的零序稳态有功功率法[10],以及同样利用故障介质击穿非线性特征的传统3 次谐波-基波相位差法[13]等。将本文算法与以上3 种代表性的高阻故障选线方法对比,讨论它们的适用场景。
选取的故障测试案例包括仿真和实测案例两类。通过在Python 建立对PSCAD 模型参数的控制接口在同图2 的配电网中批量生成仿真故障集。其中,故障点选择线路2 中部和线路3 中部两个位置;故障过渡电阻(线性部分)设为8 kΩ;谐波干扰水平设为无谐波干扰、网侧相电压THD 为1%~5%以及7%~15%三种,其中,最后一种仅作为极端条件测试;在以上三大要素排列组合的基础上,每种组合还涵盖中性点并联电感LN=L0N/3,遍历(0.30,0.62] H(步长0.04 H)、并联电阻RN=R0N/3遍历(0.1,2.0] kΩ(步长0.1 kΩ)的152 种运行场景,对 应v和d的 范 围 分 别 约 是(-0.6,0.2) 和(0.05,1.00)。因此,仿真故障测试集总计912 组。此外,另有表3 所述真型试验场的17 组高阻故障案例。不同算法的选线准确率对比如表4 所示。
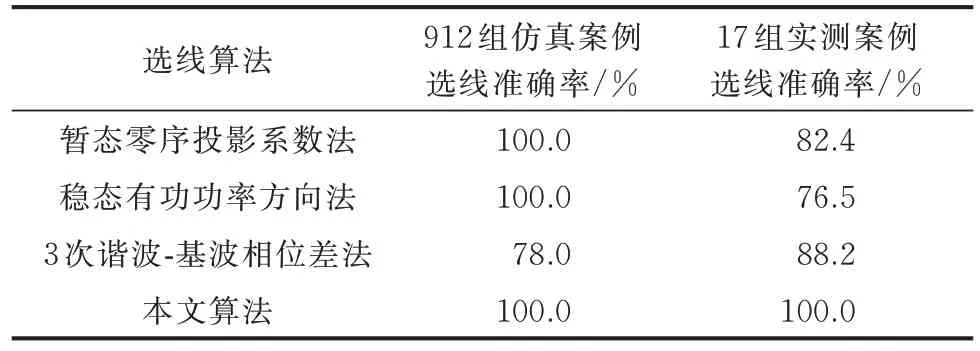
表4 不同高阻故障选线算法的可靠性对比Table 4 Reliability comparison of different highresistance fault line selection algorithms
对于故障和健全线路的零序暂态分量,分布式电源感应出的谐波电动势仅影响其幅值而不改变其极性关系。因此,所对比的暂态量法能够保证仿真故障的准确选线。但暂态量法极度依赖故障初始特征,在解决实际故障时,可能因这一阶段的极高阻值使算法面临“故障时刻捕捉不准”“初始特征受测量误差掩盖”等不易克服的难题。如附录C 图C2 给出的高阻故障电流在初始阶段因电阻达到16 kΩ 以上,超出零序电流互感器有效量程,特征难以辨识,表4 中暂态法选线错误的实测案例均与此因素有关。图C2 同时表明,本文算法可利用介质击穿的发展性,在高阻介质电阻烧蚀至5 kΩ 左右时(故障后约30 个周期),特征量满足判据要求,实现准确选线。
对于表4 中的另两种对比算法,稳态有功功率方向法要求在故障发生后于中性点投入并联电阻,因此,需在中性点增设控制系统;并且此类方法基于工频分量,因此对于间歇性故障时不易平衡相量计算窗口和测量精度,易产生相位误差而误判。另外,3 次谐波-基波相位差法利用高阻非线性时3 次谐波和基波相位相反的特点,但这种关系仅存在于电流过零点附近。因此,此种相位关系和过零点的追踪均容易受到间歇性和谐波源的干扰,导致选线错误。
综上所述,本文方法具有以下优势:1)兼具暂、稳态特征的有效提取能力,不完全依赖于故障初始阶段特征,规避了高阻故障发生时刻精准标定以及初始特征辨识的抗干扰问题;2)本文方法在原理上受过渡电阻影响小、对系统运行场景适用范围广、抗分布式电源非线性运行的干扰能力强;3)利用频段特征信号,相比于工频特征量,特征提取对间歇性接地更具鲁棒性。因此,本文方法综合性能更优。
5 结语
针对当前配电网高阻故障选线技术耐过渡电阻能力受限、对分布式电源接入等复杂系统运行方式下适用性不强等技术难点,本文探讨了高阻故障介质击穿过程的非线性特征及其在高阻故障选线中的重要潜力,建立含分布式电源配电网零序等值网络,推导了基于幅值和相角因子的宽频带零序信号关于系统运行参数的数学表达式,讨论了故障时宽频信号空间分布规律,并以此构建了高阻故障选线特征量和判据。理论分析和案例验证表明,以低阶奇次谐波为核心所构建的频段信号是谐振接地系统高阻故障选线的最优特征信号。本文基于此构建的频段无功功率特征量及选线判据兼具暂态和稳态故障特征的辨识能力,并且选线效果在对系统运行方式的适用性、对分布式电源非线性的鲁棒性、抗干扰能力等方面具有综合优势。
本文方法的应用依托零序电压和电流信号的高精度采集,可应用于具备测量条件的变电站内的故障选线应用中。目前,在中压配电网架空线路上,一般不具备零序信号(尤其是零序电压)的采集条件。因此,本文方法仅适用于高阻故障的选线,进一步推广至故障区段的隔离和自愈还需要配电网设备的大范围改造升级。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
