基于模拟退火算法的民航运输路径优化技术研究
2023-10-21王珺
王珺
(西安航空职业技术学院,陕西西安 710089)
民航运输具有速度快、效率高的特点,但也较易受到其他因素的影响。例如空中资源分配不均、航线延误及运输上座率低等问题,均会大幅增加民航运输的成本[1]。而解决此类问题的有效途径之一,便是对民航运输路径进行优化。
传统的民航路径选择算法使用专家经验法,该方法主观性较强、稳定性较差、效率也较低,且无法有效地降低成本。该文对民航货物运输路径选择[2]问题进行了研究,并针对运载情况复杂多变、航线选择困难等问题,使用带时间窗[3]的路径优化算法来对该问题进行建模。同时将模拟退火算法(Simulated Annealing,SA)[4-6]和遗传 算法(Genetic Algorithm,GA)[7-9]相结合并进行改进,使算法兼具局部求解和全局求解能力。为验证该文所提算法,使用Matlab进行建模,并与其他路径优化算法相对比,验证了该文算法的优异表现。
1 带时间窗的民航运输路径模型建立
1.1 场景建立
民航运输的特点是对运输时长较为敏感,因此,该文建立了带有时间窗的民航运输路径模型。
假设民航班机从某个中心机场出发,并按照运输节点要求完成运输任务,最后返回中心机场。中心机场是飞机的起飞点,在其完成所需货物或乘客的运输后会重新返回。
1.2 目标函数
该文目标函数由3 个函数体组成,分别为总里程成本、时间变化成本以及机组成本。
1)总里程成本
班机的运输成本[10]主要为燃油费,其与运输距离呈正相关。故在配送时,需选择配送路径距离最短的一条。运输成本可表示为:
式中,c表示单位距离运输成本,i、j表示目标节点的序号,k表示班机的序号,dij表示节点i到节点j之间的距离。
2)时间变化成本
对于时间窗模型而言,在规定时间内将货物运送至指定地点可节省成本。假设货物到达的时间区间为[T1,T2],Ti为第i架班机达到的时间,则时间损失成本如下:
式中,a和b为班机提早到达与晚点到达的单位时间损失成本。
3)机组成本
机组成本主要是班机的保养及维护费用,而固定成本与同一航线的航班数量也有关系,其可表示为:
式中,C为单架班机的固定费用,Nk为第k架班机,sign 作为符号函数可判断班机的使用情况。
1.3 模型建立
由上文所述,最终得到的目标优化函数如下所示:
式(7)表示中心机场的班机执行完配送任务后,再次装载货物返回中心机场。式(8)表示中心机场完成运输任务共需m架班机。式(9)中,Q表示班机的最大载重量,qi表示节点i所需的货物,该公式表明目标节点所需物流量不能超过班机的最大载重量。式(10)中,L表示班机最长运输距离,该式表明班机运输距离不可超过自身最长行驶距离。
2 遗传模拟退火算法
2.1 模拟退火算法
模拟退火算法[11]由物理原理模拟得到,在金属冶炼过程中金属受热会发生融化,当停止加热后则会重新固化,这也是对问题最优解进行搜索的过程。该算法的优点是能对全局最优解加以搜索并避免算法陷入局部解中,同时其无需函数初值即可得到结果。
使用数学模型对模拟退火过程进行描述,其自适应状态函数可由式(11)表示:
由式(11)可知,E(i)和E(j)是模拟退火过程中的两个能量状态。当E(i)>E(j)时,表明状态能被正常切换;而当E(j)>E(i)时,切换状态成功概率则将大幅降低。上式中,K为时间常数,T为金属温度。
模拟退火算法的基本步骤如图1 所示。其在局部搜索中的优势较大、概率跳变特性显著并具有较强的鲁棒性。但同时该算法的参数依赖性也较强、迭代次数多且算法效率较低,因此需对其进行改进。
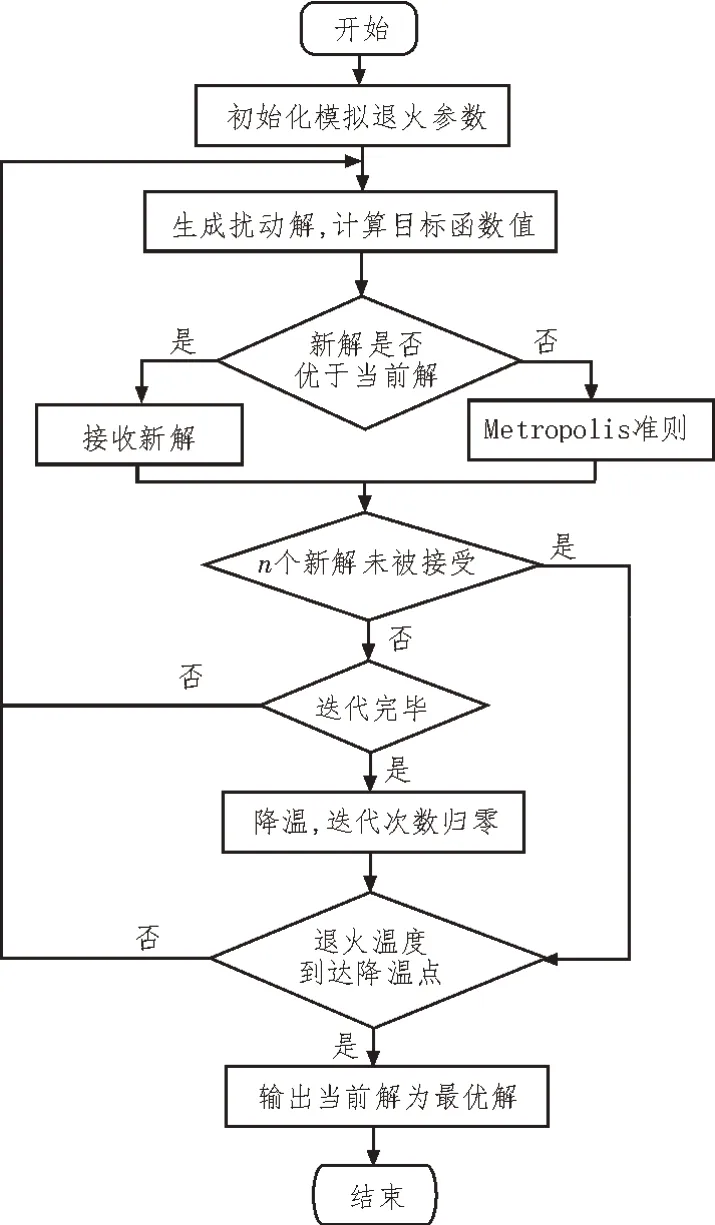
图1 模拟退火算法实现流程
2.2 改进的遗传模拟退火算法
遗传算法主要用来求解组合优化问题[12],其可将多个问题看作是一个种群,问题的解则看作是种群的最优化繁殖。数学模型主要是将组合问题的目标函数转换成适应度函数,同时根据该函数对个体加以筛选。然后个体进行交叉[13]、变异[14]等操作,使自身适应度不断增加,进而形成种群的最优解。
由遗传算法求解过程可知,该算法有较强的全局搜索性,故在求解组合问题时容易收敛,因此迭代次数过少将难以求得最优解。
遗传模拟退火算法将遗传算法与模拟退火算法相结合,可有效提升模拟退火算法的运行效率及遗传算法的局部解搜索能力。遗传模拟算法实现的流程如图2 所示。
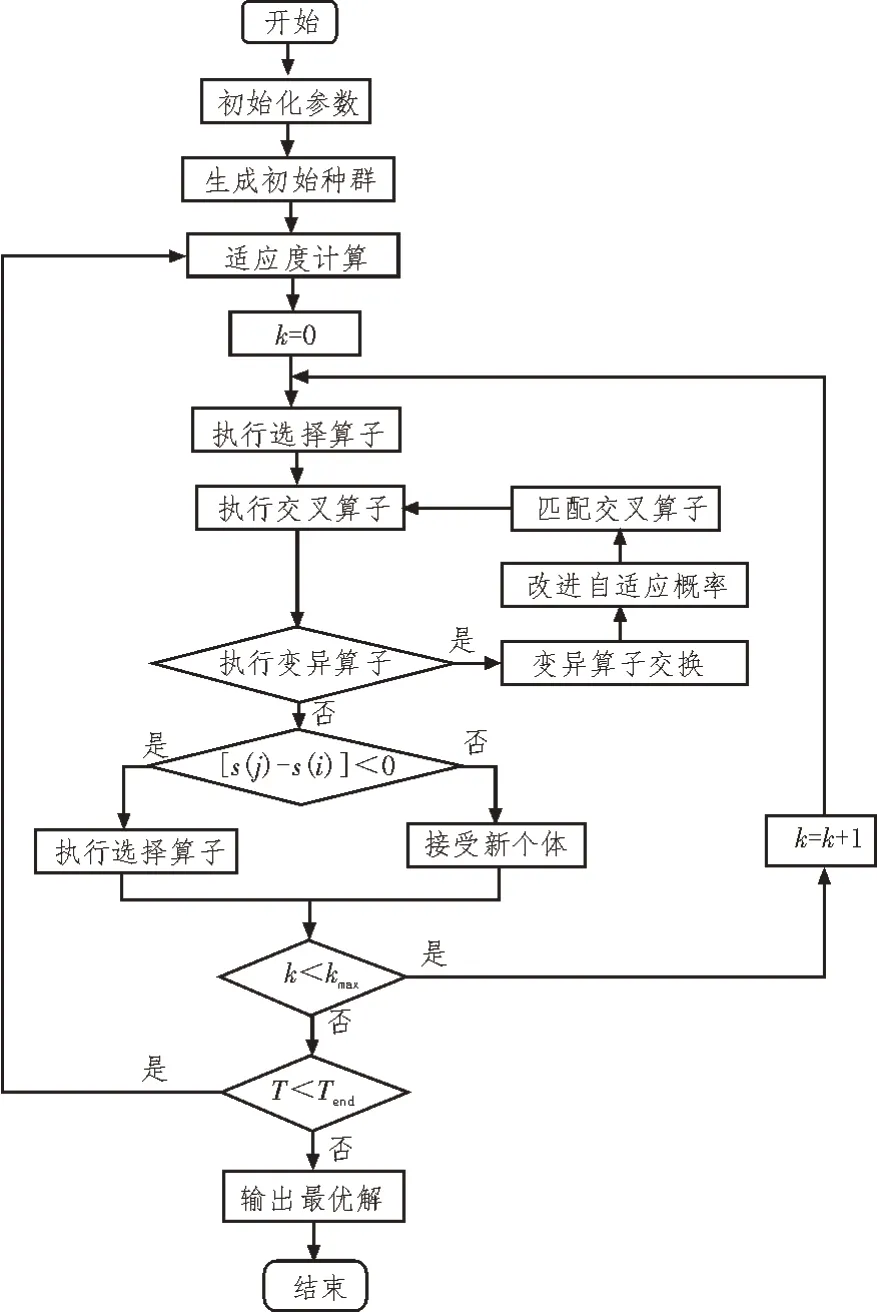
图2 遗传模拟算法实现流程
该文对遗传模拟算法进行了改进,以便充分发挥算法的局部求解和全局求解能力。改进之处共有两点:
1)在计算初始阶段,算法进行局部求解,但此时易陷入局部最优,因此使用混沌理论(Chaos theory)初始化种群。该文使用的Logistic混沌公式如下:
式中,Θ为混沌公式的控制变量,yn为第n次迭代的值,yn+1则为第n+1 次迭代的值。该公式通过动态的映射能够充分保持种群多样性,从而避免计算进入局部最优的状态。
2)在遗传模拟退火算法中,遗传算子的选择与计算较为重要,文中使用自适应公式对图2 中的遗传算子(交叉算子、变异算子)进行改进,由此便可使遗传算法随着适应度的变化而改变。
交叉算子及变异算子的自适应函数如下所示:
上式中,pc和pm为交叉算子及变异算子,pc1和pc2为交叉算子的控制系数,pm1和pm2则为变异算子控制系数,f为遗传算法适应度,fmax与favg分别为算法的最大适应度和平均适应度。
因此,该文算法的具体流程如下:
1)初始化参数,包括退火算法的初始、结束温度以及遗传算法的交叉、变异概率;
2)使用混沌理论Logistic 混沌公式进行种群初始化;
3)计算种群适应度、平均适应度及最大适应度,并对种群个体进行选择;
4)使用自适应函数优化交叉算子与变异算子,以得到最优的个体适应度;
5)遗传算法输出性能和状态最优的个体;
6)数据输入至模拟退火算法,再由其求得最终解。
3 算法测试
3.1 数据训练
该文使用有时间窗路径优化问题(Vehicle Routing Problems with Time Windows,VRPTW)[15-16]专用的Soloman 数据集。该数据集包含有56 个算例,文中使用其对民航班机的货物运输过程进行模拟。算例所包含的数据类型也较多,包括配送目的地坐标、需求货量、中心机场班机数量与班机最大载重量等。
同时为了验证模型的性能,还使用了Matlab 进行编程仿真。所采用的硬件平台如表1 所示。

表1 硬件环境
3.2 仿真结果分析与对比
在算法仿真中,对数据集算例进行了相应运算并得到了算法最优值,再将其与数据集最优值、其他算法运算最优值加以对比。算法总体的路径优化目标即路径最短、运输班机最少,同时多次求解保证算法的客观性。对比算法选用了模拟退火算法(算法1)和遗传算法(算法2),而算法评估指标则为班机数量求解误差值与里程求解误差值。仿真求解结果如表2、3 所示。
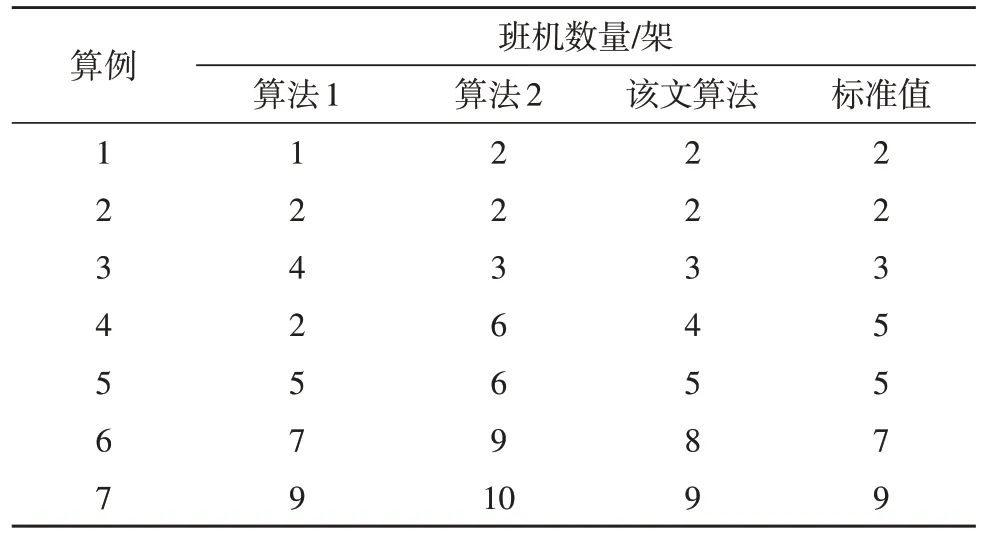
表2 班机数量求解结果

表3 飞行里程求解结果
由上表可以看出,该文算法在不同算例中的表现也有所不同,由于航班数与配送点数正相关,因此从算例1 到算例7,其配送点数均在不断增加。由于遗传算法的全局特性较好,因此在简单场景下的优势更大。模拟退火算法在复杂场景下的表现更优,显示出其优良的局部求解能力。而该文算法的误差率在每个算例中整体较为平均,这也表明其兼具局部求解和全局求解能力。而对于该文算法而言,迭代次数指标也是关键的一项。算例2 的迭代过程如图3 所示。
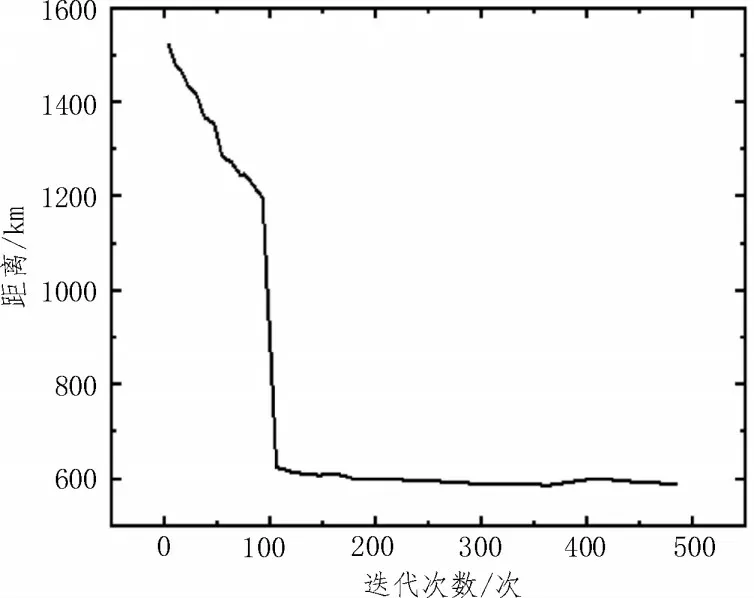
图3 算例2的迭代过程
图3 中纵坐标表示的是求解距离,横坐标则表示算法的迭代次数。由图可知,在算法运行初期,计算距离在不断下降,表明该文算法可在短时间内靠近最优求解值。而随着迭代次数的增加,求解值也趋于稳定。这也说明了该算法兼具模拟退火算法与遗传算法的优点,且具有良好的收敛性及稳定性。
4 结束语
民航运输是我国物流运输体系中的重要一环,而运输路径的选择对民航运输的成本影响较大。传统的航空路径选择主要依靠人工经验指导,其主观性较强且稳定性较差。该文对遗传模拟退火算法加以改进,使用了混沌理论初始化种群,并对变异算子和交叉算子的实时性进行了自适应优化。在建模实验中,该文算法的班机数量求解与实际值相差最小,且拥有较快的收敛速度,由此证明了该文算法的性能优良,并可应用于实际工程中。
