基于多新息辨识算法的锂离子电池等效电路模型参数辨识

林 鹏，刘 涛，金 鹏，王震坡，王生捷，袁红升，马 泽，狄 宇

（1北京机械设备研究所，北京 100854；2中国人民解放军63936部队，北京 100024；3北京理工大学机械与车辆学院，电动车辆国家工程研究中心，北京 100081；4北方工业大学电气与控制工程学院；5北京电动车辆协同创新中心，北京 100144）

锂离子动力电池在车辆、储能领域有着广泛应用，有助于降低我国对石油的依赖、推动能源绿色转型，然而其使用过程极易发生过充、过放等安全事故[1-4]。为保障动力电池的安全使用，须通过电池管理系统(battery management system，BMS)对其电压、电流、温度进行监测，准确估计其状态及控制其充放电过程。获得精确的电池模型参数可有效地提高电池状态估计精度，保障电池充放电安全，是BMS的核心技术之一[5-10]。

常用的电池模型分为经验模型、电化学模型和等效电路模型。其中经验模型只能反映电压与荷电状态(state of charge，SOC)、电流之间的近似关系，无法准确描述电池的瞬态特性，应用范围较小。而电化学模型虽能精确地描述电池的静动态特性，但其结构复杂、求解困难，这限制了它的应用场景。RC(resistance-capacitance)等效电路模型能够较好地描述电池的静动态特性，在电池仿真、分析和估计电池状态等领域应用广泛[11-12]。根据RC环节的个数，RC等效电路模型主要分为：零阶RC等效电路模型、一阶RC 等效电路模型、二阶RC等效电路模型和多阶RC 等效电路模型。二阶模型包含二阶RC 等效电路模型和PNGV(partnership for a new generation of vehicles)模型。虽然二阶RC等效电路模型比Thevenin模型(即一阶RC等效电路模型)多一个RC 环节，但二阶RC 等效电路模型并不复杂，其精度比Thevenin 模型高。PNGV模型能够反映电流的累积效应对开路电压(opencircuit voltage，OCV)的影响，该模型也常应用于电池特性分析和状态估计[13-18]。

获得精确的电池模型参数可提高电池仿真和状态估计的精度，电池模型参数的计算方法分为离线辨识/计算和在线辨识。将极化过电势作为电流的响应，通过离散的方式得到能够辨识的差分方程，利用粒子群算法、遗传算法、最小二乘法等算法即可辨识RC 等效电路模型的参数[9,19-24]。刘志聪等[25]通过Z 变换的方式将二阶RC 等效电路模型转化为可辨识的差分方程，并利用带遗忘因子的递推最小二乘法实现了电池模型参数的辨识。杜帮华等[26]为了跟踪老化电池的模型参数，提出了可变遗忘因子的最小二乘法。为了解决RC 等效电路模型参数在线辨识的问题，熊瑞[27]提出了N阶RC 等效电路模型的辨识方法，并利用带遗忘因子的最小二乘算法实现了包含OCV在内的模型参数辨识。

PNGV模型的参数辨识主要有离线计算的方式和曲线拟合的方式。该模型存在的纯电阻环节可利用电压和电流的瞬变求得，等效电容可利用OCV随电流累积效应的变化进行计算，根据零状态和零输入响应求得RC 环节的参数[14,16,28-31]。将OCV 与端电压的差值作为输出，在均方根误差最小的准则下，利用遗传算法对输出进行拟合，从而得到PNGV模型的参数[32]。电流、温度等因素都会对电池特性产生影响，因此目前的方法无法实现PNGV模型参数的在线精确辨识，进而限制了该模型的使用。

在给定的期望指标下，优化算法按照某些原则在指定的数据集中选择最佳的参数值，使得系统输出的性能指标达到最优。因此基于优化算法的等效电路模型参数辨识常会陷入局部最优状态，无法达到整体最优，而且无法实现实时、在线的参数辨识。在最小二乘一类的辨识算法中，总是采用前一时刻的参数估计值加上当前的预报误差与增益向量的乘积来校正新的参数估计值，这样虽然能够快速跟踪等效电路模型的参数，但存在收敛速度慢、估计精度低等缺点。即使在最小二乘算法中引入遗忘因子，逐渐消除旧数据对参数辨识的影响，该算法也依旧采用单一时刻的预报误差修正当前时刻的参数估计值，并忽略了大量有用的信息，导致该类算法存在鲁棒性差、精度低等问题。

由电池的建模过程可知，电池为非线性时变系统，电池的特性受到电流倍率、工况、温度和老化程度的影响。电池老化程度的改变必将影响等效电路模型的参数，当前的辨识算法对不同老化程度下电池模型参数的辨识精度缺少进一步验证。由于电动汽车的实车工况异常复杂且变化较快，需采用实时性好、收敛速度快和精度高的辨识算法才能准确获得电池的实时参数，进而实现BMS 对电池的安全及有效管理。因此，构建实时性好、精度高的参数辨识算法是BMS亟须解决的问题。

为了提高模型参数辨识的精度，本文提出了带遗忘因子的多新息辅助模型扩展递推最小二乘算法，并与常用的系统辨识算法进行了对比分析，说明了该算法的优势。本工作的主要贡献有：

（1）建立了同时获得二阶RC 等效电路模型和PNGV模型参数的、统一的辨识方程。

（2）基于多新息辨识方法，提出了带遗忘因子的多新息辅助模型扩展递推最小二乘算法，在不同温度、工况和老化状态下实现了等效电路模型参数的精确辨识。

（3）实现了OCV的精确辨识，为SOC的精确估计奠定了基础。

本文首先介绍了等效电路模型参数的辨识方法，然后根据多新息辨识理论推导了基于多新息的等效电路模型参数辨识算法，最后在不同温度、工况和老化程度下验证了该辨识算法的精度。

1 等效电路模型参数的辨识方法

1.1 二阶RC等效电路模型

如图1所示的二阶RC等效电路模型考虑了电池正负极的极化特性，该模型可表示为式(1)～式(3)。

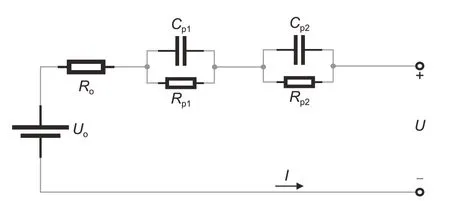
图1 二阶RC等效电路模型Fig.1 2-order RC equivalent circuit model

式中，Uo为OCV；Ro为欧姆内阻；Rp1、Rp2为极化内阻；Cp1、Cp2为极化电容。这些参数为待辨识参数。

将式(1)～式(3)转化为如式(4)～式(6)所示的差分方程：

式中，a1、a2、b1、b2为系数。

并将式(5)和式(6)分别代入式(4)，并经过变换得：

由于采样时间很短，Uo几乎不发生变化，所以Uo,k=Uo,k-1=Uo,k-2，由式(7)可以得到二阶RC等效电路模型的差分方程：

1.2 PNGV模型

在电流的累积作用下，OCV 会发生偏移。为了描述这个特性，PNGV模型利用等效电容Cb描述OCV随电流累积效应的变化。如图2所示的PNGV模型可表示为：

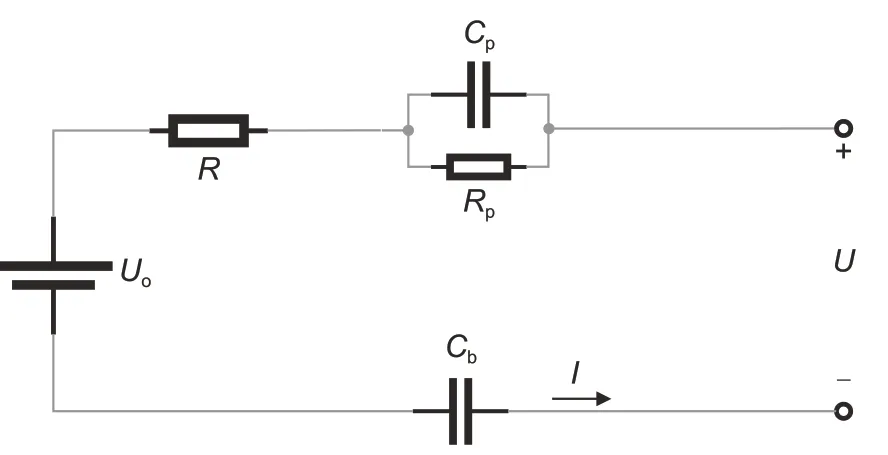
图2 PNGV模型Fig.2 PNGV model

将式(9)～式(11)分别转化为差分方程：

式中，Uo、R、Rp、Cp和Cb为待辨识参数。

与1.1 节的变换方法类似，可以得到PNGV 模型的差分方程：

注意到，若将式(15)中Uo的系数直接展开，Uo将被消除进而无法求解。由于Uo的系数是Uk-1和Uk-2系数的组合(该结论与二阶RC 等效电路模型的形式和文献[33，34]的结论一致)，为了能够求得Uo，在此做一个巧妙的变换：将Uk-1和Uk-2的系数分别看成一个整体，并将Uo的系数看作它们的组合，则Uo可体现在式(15)中，进而求得Uo。

1.3 统一的等效电路模型参数的辨识方程

为了方便比较二阶RC 等效电路模型的差分方程和PNGV 模型的差分方程的特点，将式(8)和式(15)分别简化为式(16)和式(17)。

对于二阶RC等效电路模型则有：

由式(16)和式(17)可知，二阶RC 等效电路模型的差分方程与PNGV模型的差分方程具有相同的形式和结构。因此，可同时辨识二阶RC 等效电路模型和PNGV模型参数的方程如式(18)所示。

将式(18)改造为最小二乘格式：

其 中，yk=Uk，θ=[α0α1α2β0β1β2]，ϕ=[1k yk-1yk-2IkIk-1Ik-2]。

进而θ与二阶RC 等效电路模型和PNGV 模型参数之间的关系可表示为：

特别地，当模型为PNGV模型时，a2= 1。

当等效电路模型为二阶RC 等效电路模型时，式(20)中的变量与二阶RC 等效电路模型的参数之间的关系为：

当等效电路模型为PNGV模型时，式(20)中的变量与PNGV模型参数之间的关系为式(22)。

利用式(20)和式(21)即可计算包含OCV在内的二阶RC 等效电路模型的参数，而利用式(20)和式(22)即可计算包含OCV在内的PNGV模型的参数。

由式(21)和式(22)可知，若能辨识式(19)中的θ即可计算二阶RC模型和PNGV模型的参数。

2 多新息辨识算法

2.1 带遗忘因子的多新息辅助模型扩展递推最小二乘算法

由于锂离子动力电池为非线性时变系统，表现在模型参数上就是时变参数。虽然递推增广最小二乘算法(recursive extended least squares algorithm，RELS)具有递推最小二乘算法的所有优势，在有色噪声下可实现模型参数的无偏估计和一致性估计[35]，但存在辨识精度低、收敛速度慢等缺点，不能解决数据饱和问题，进而无法实现时变参数的实时跟踪。因此，RELS并不适用于锂离子动力电池的模型参数辨识。

若将单一误差(称为单一新息)标量扩展为一个m维(m＞1)的误差向量(称为多新息)，增益向量扩展为一个增益矩阵，利用多新息与增益矩阵校正新的参数估计值[36]，这种新的辨识思想称为多新息系统辨识理论[36-37]。多新息系统辨识算法不仅可以加快收敛速度，提高辨识精度，同时可以抑制坏数据或者缺失数据对参数辨识结果的影响，提升辨识算法的鲁棒性。

多新息模型参数辨识理论具有辨识速度快、精度高、鲁棒性好等优势，而RELS可实现模型参数的无偏估计和一致性估计，若将两者的优势结合起来就能实现精度高、收敛快的锂离子动力电池模型参数的辨识。

因此，带遗忘因子的多新息辅助模型扩展递推最小二乘算法(multi-innovation auxiliary model extended recursive least squares algorithm with forgetting factor，FMIAELS)可表示为：

详细推导过程见附录。

2.2 常用的系统辨识算法

为了说明FMIAELS 在电池模型参数辨识上的优势，利用常用的系统辨识算法与该算法进行对比分析。常用的系统辨识算法有RELS[38]、带遗忘因子的递推最小二乘算法(recursive least squares algorithm with forgetting factor，FRLS)[39-41]、递推随机牛顿梯度校正算法(recursive stochastic newton gradient correction algorithm，RSNA)[42-43]、模型参考自适应系统(model reference adaptive system，MRAS)[44-45]和智能优化算法。

在智能优化算法中，差分进化算法(differential evolution algorithm，DE)是一种较好的智能优化算法，该算法以“优胜劣汰，适者生存”为原则，具有简单易用和搜索能力强等优势，适用于系统的参数辨识领域[46]。基本的差分进化算法中的变异算子如果变异率太大，算法执行的效率很低，所求得的全局最优解精度也很低；若变异率太小，种群多样性就会降低，易出现“早熟”现象。若变异算子能够根据最优解的情况自动变化，可避免出现上述情况。针对这样的问题，衍生出自适应差分进化算法(adaptive differential evolution algorithm，ADE)[47]。

2.3 系统辨识算法的性能评价指标

为了评价系统辨识算法的精度，采用平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)和加权平均绝对百分比误差(weighted mean absolute percentage error，WMAPE)作为性能评价的指标。MAE、RMSE 和WMAPE 由式(24)～式(26)给出。由这些指标的定义可知，它们的值越小，说明系统辨识算法的辨识效果越好，辨识精度越高。

式中，L为数据的总数；Ureal为真实端电压；Uestimated为采用某种系统辨识算法所估计的端电压。

3 电池特性测试

本文所选电池为方形60 Ah/3.2 V 的LiFePO4动力电池。测试平台包含Digatron BNT 300-060 ME电动汽车动力电池测试设备及其控制软件和Terchy可程式恒温恒湿试验机MHX-408NKM。

电池模型参数辨识的测试脉冲(图3)采用多个正负脉冲(脉冲幅值依次为2 C、1.5 C、1 C、0.5 C和0.25 C，正负脉冲各持续10 s，简称MPN)、多个负正脉冲(脉冲幅值依次为2 C、1.5 C、1 C、0.5 C和0.25 C，负正脉冲各持续10 s，简称MNP)和HPPC(hybrid pulse power characteristic)脉冲(负脉冲幅值为2 C)。为了分析不同温度和测试工况下电池模型参数辨识的精度，在5 ℃、10 ℃和35 ℃的温度下对电池进行GB 工况、DST 工况和FUDS工况的测试①GB工况：《GB/T 31484—2015 电动汽车用动力蓄电池循环寿命要求及试验方法》中“纯电动乘用车用能量型蓄电池”里的“主放电工况”。DST工况：dynamic stress test工况。FUDS工况：federal urban driving schedule工况。。

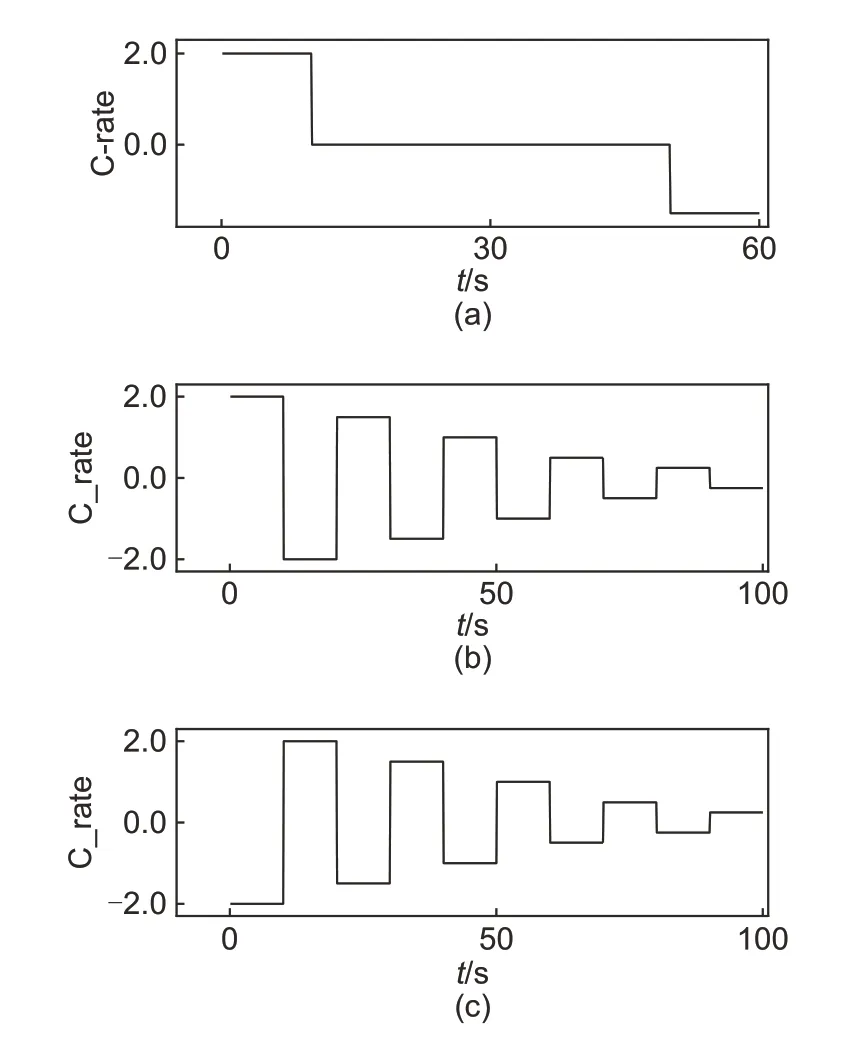
图3 测试脉冲：(a) HPPC脉冲，(b) MPN脉冲，(c) MNP脉冲Fig.3 Test pulses: (a) HPPC, (b) MPN, (c) MNP

为了创造不同的老化程度，电池老化实验采用恒流恒压的方式进行，采用1 C 电流进行满充满放，实验温度为25 ℃。

4 辨识结果分析

4.1 脉冲工况下的仿真结果

4.1.1 二阶RC等效电路模型的仿真结果

图4 展示了MPN 脉冲下利用各算法辨识的二阶RC 等效电路模型参数仿真的端电压的实时结果。相比RELS、FRLS和ADE，FMIAELS辨识的参数更精确，其模型仿真值更接近于真实的端电压[图4(a)]。由表1的性能评价指标可知，FMIAELS在MPN 脉冲下辨识的模型参数仿真的端电压的MAE、 RMSE 和WMAPE(1.18 mV、 1.89 mV、0.04%)均小于RELS(5.80 mV、6.90 mV、0.18%)、FRLS(3.18 mV、3.85 mV、0.10%)和ADE(8.98 mV、4.86 mV、0.19%)。

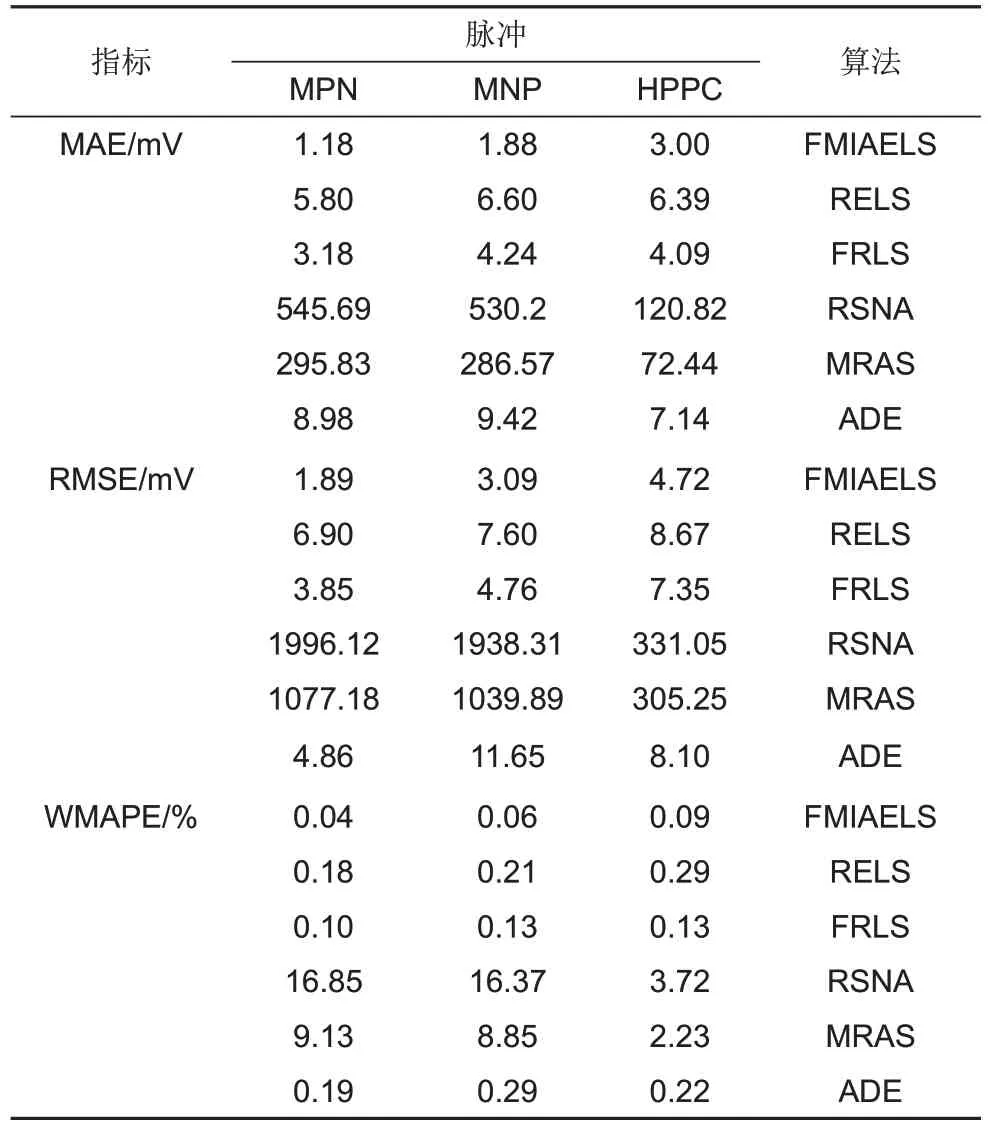
表1 在不同脉冲作用下二阶RC等效电路模型的仿真误差Table 1 Simulation error of the 2-order RC equivalent circuit model under different pulses

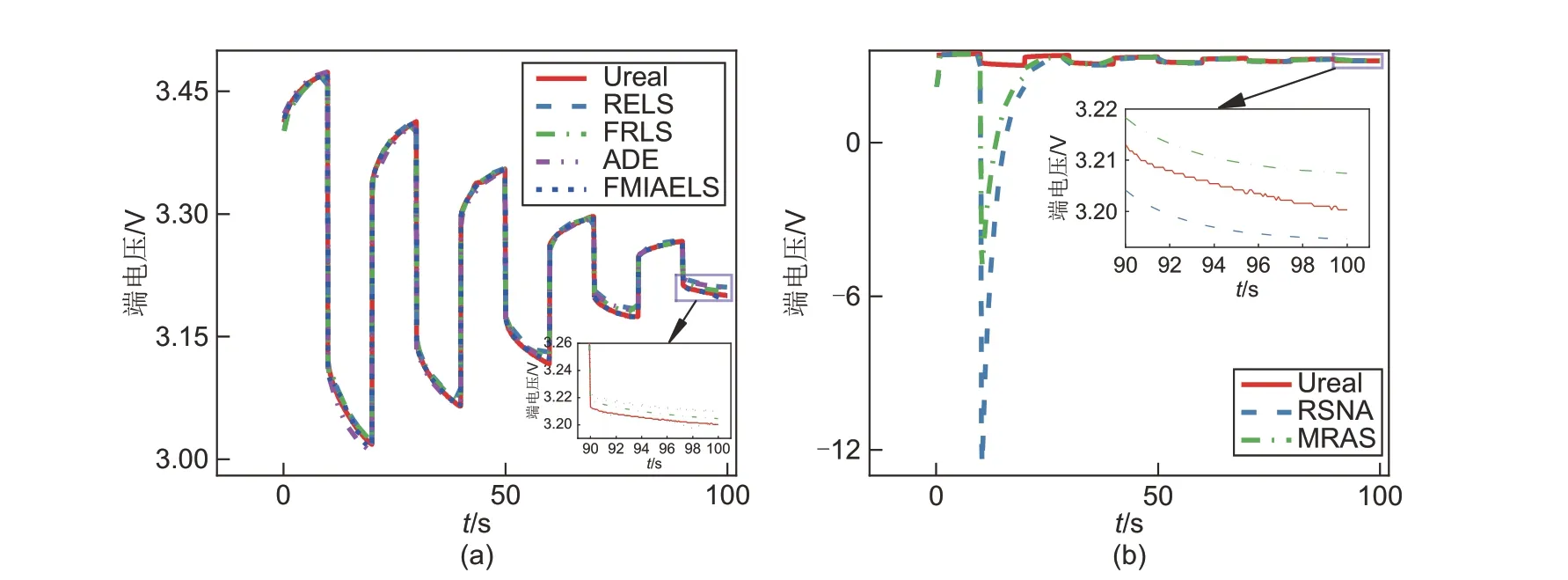
图4 MPN脉冲下二阶RC等效电路模型的端电压仿真结果Fig.4 Simulation results of the 2-order RC equivalent circuit model under the MPN pulse

RSNA 和MRAS 所辨识的二阶RC 等效电路模型的参数误差很大，导致MPN 脉冲下在第一个正脉冲向负脉冲转变时，端电压的估计值与真实值相差很大，最大误差分别高达15.7102 V和7.9528 V[图4(b)]。由于RSNA和MRAS具备误差修正能力，当端电压的估计值存在较大误差时，这两种算法利用估计误差修正新的估计值，因此它们分别于19 s和15 s的所估计的端电压误差小于0.1 V，在此之后估计误差越来越小，最终RMSE分别为1.99612 V和1.07718 V。因此，RSNA 和MRAS 不适合作为电池模型参数的辨识算法。

对于MNP 脉冲和HPPC 脉冲，如表1 所示，FMIAELS辨识的二阶RC等效电路模型的参数依然具有最高的精度，其端电压的MAE、RMSE 和WMAPE都比RELS、FRLS和ADE小，而比RSNA、MRAS分别小了约1个数量级。因此，在不同的脉冲工况下，FMIAELS辨识的二阶RC等效电路模型的精度和实时性优于常用的系统辨识算法。

4.1.2 PNGV模型的仿真结果

在MPN 脉冲下，利用各算法辨识的PNGV 模型的参数仿真的端电压如图5 所示。FMIAELS 的精度依然高于RELS、FRLS、RSNA 和MRAS，如图5(a)、(b)所示。ADE 辨识的PNGV 模型参数为全局最优参数，在此阶段内端电压的仿真值要比FMIAELS 略为精确(图5 和表2)。由于锂离子动力电池为非线性时变系统，在电流累积的作用下，电池的特性会发生变化，进而影响PNGV 模型参数，因此FMIAELS 在MPN 脉冲后期的估计精度优于ADE的估计精度[图5(a)]。

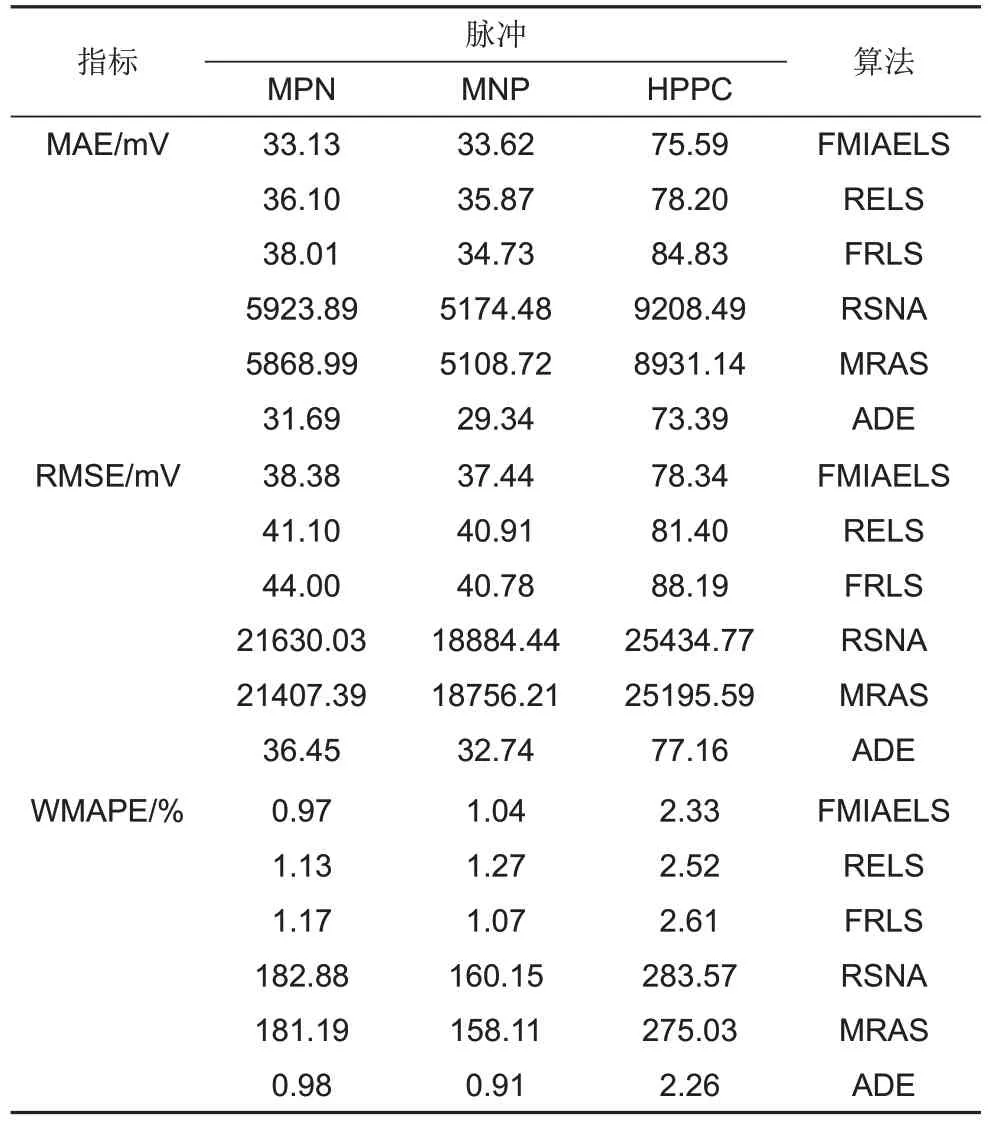
表2 在不同脉冲作用下PNGV模型的仿真误差Table 2 Simulation error of the PNGV model under different pulses

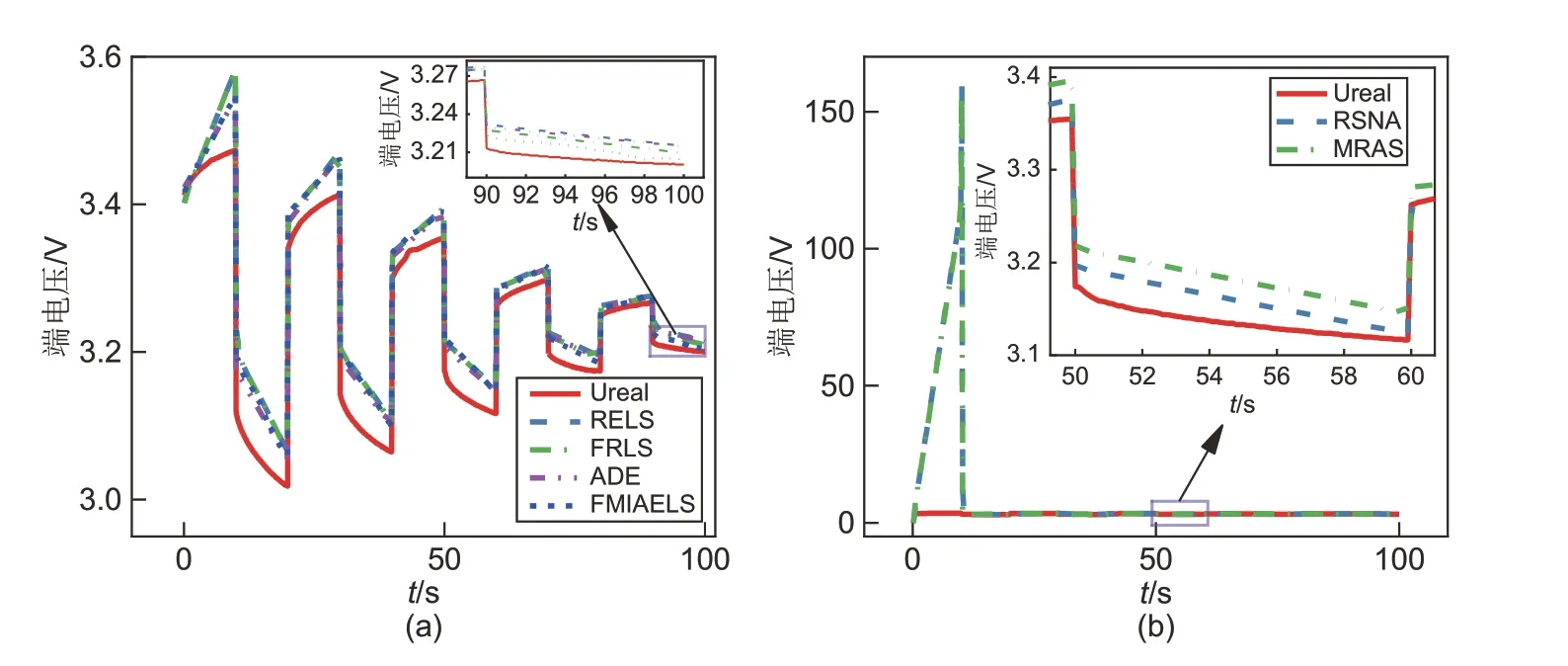
图5 MPN脉冲下PNGV模型端电压的仿真结果Fig.5 Simulation results of the PNGV model under the MPN pulse

表2 展示了在MPN、MNP 和HPPC 脉冲作用下，各算法辨识的PNGV模型参数仿真的端电压的误差。由表2 的结果可知，在MNP 和HPPC 脉冲作用下FMIAELS 的精度均高于RELS、FRLS、RSNA 和MRAS。由于ADE 能够估计全局最优参数，其精度略高于FMIAELS，但该算法无法实时地辨识参数，进而无法应用于实际工况下的电池模型参数辨识。

综合4.1.1节和4.1.2节的分析可知，PNGV模型的精度低于二阶RC 等效电路模型的精度，其RMSE大约为二阶RC等效电路模型的16倍(表1和表2)。而且PNGV 模型仿真的端电压会在整个HPPC工况中随着电流的累积而出现很大偏移[48-49]，使得该模型无法准确仿真电池的特性。文献[50]也说明了二阶RC 等效电路模型的精度高、性能好，因此，二阶RC 等效电路模型更适合模拟电池的特性。

4.1.3 零阶和一阶RC等效电路模型的仿真结果

为了进一步说明FMIAELS的优势，对零阶RC等效电路模型(即Rint 模型)和一阶RC 等效电路模型的参数进行了辨识，并利用辨识的模型参数仿真了电池的端电压。零阶RC等效电路模型和一阶RC等效电路模型的参数方法参照1.1 节的方法即可得到，这里只展示仿真结果。由于RSNA和MRAS的精度较低，本节不再分析它们的精度。

FMIAELS和常用的系统辨识算法在MPN脉冲下辨识的零阶RC 等效电路参数仿真的端电压的结果如图6 所示。由于RELS、FRLS 和ADE 是按照残差平方和最小为准则的辨识算法，在辨识只有2个参数的零阶RC 等效电路模型时，整体残差对辨识结果影响很大，所辨识的OCV 和集总内阻均是该阶段的平均值，导致这些算法的精度低，所估计的端电压接近于10 s脉冲内端电压的平均值，进而无法模拟电池的非线性特性。FMIAELS 是按照多新息辨识理论建立的算法，该算法利用多个新息来校正零阶RC 等效电路模型的参数估计值，引入遗忘因子后消除了旧数据对参数辨识精度的影响，它的精度优于RELS、FRLS 和ADE。由表3 可知，在不同的脉冲作用下，FMIAELS所辨识的零阶RC等效电路模型的精度均高于常用的系统辨识算法。在MPN脉冲下，其MAE仅为RELS算法的1/4左右。

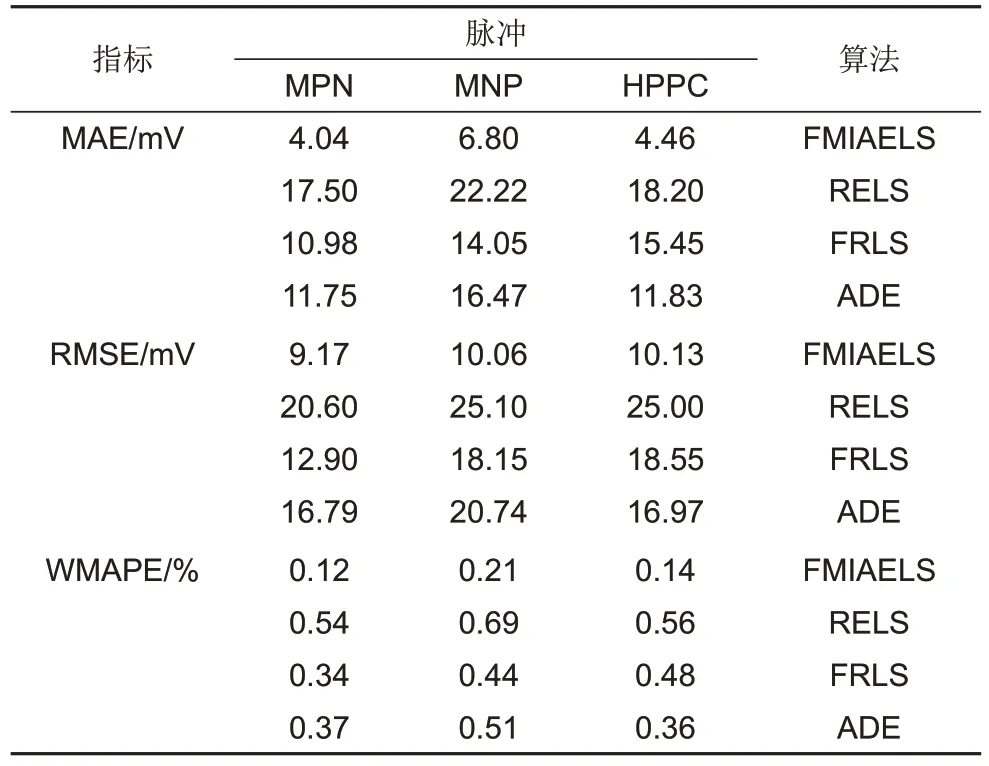
表3 零阶RC等效电路模型的仿真误差Table 3 Simulation error of the 0-order RC equivalent circuit model

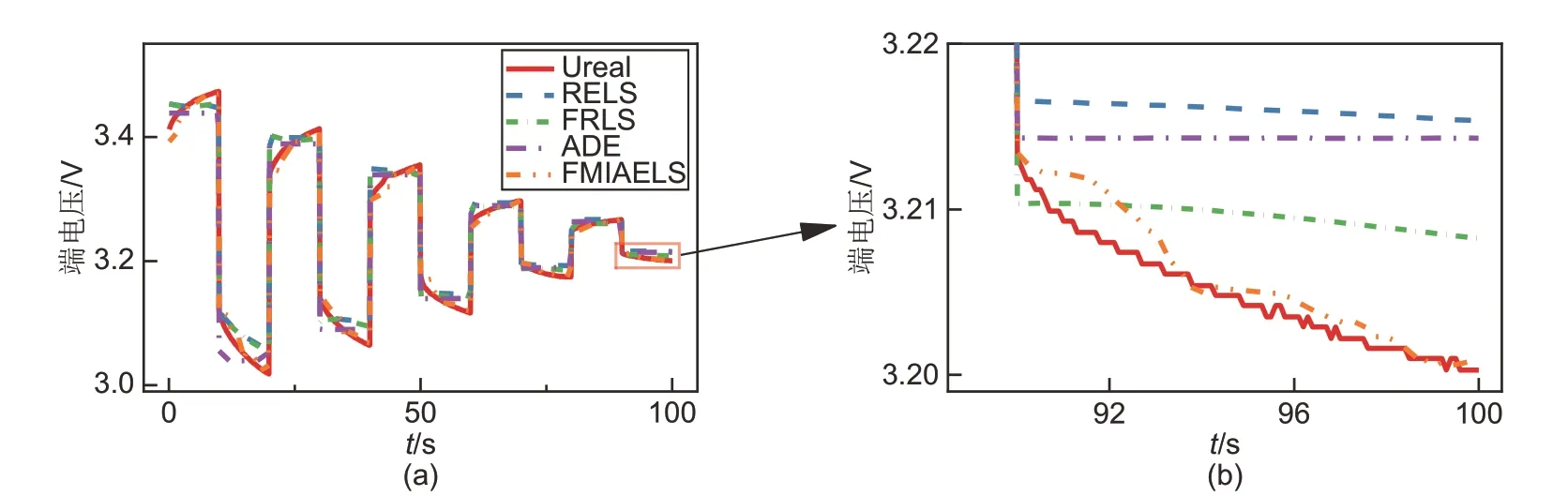
图6 在MPN脉冲下零阶RC等效电路模型的仿真结果Fig.6 Simulation results of the 0-order RC equivalent circuit model under the MPN pulse

在不同的脉冲作用下，FMIAELS 和常用的系统辨识算法辨识的一阶RC 等效电路模型参数仿真的端电压的误差如表4 所示。由表4 可知，在不同脉冲作用下，FMIAELS 辨识的一阶RC 等效电路模型的精度均高于常用的系统辨识算法。在MPN 脉冲下，该算法的MAE 比RELS 算法的至少低了1/2。

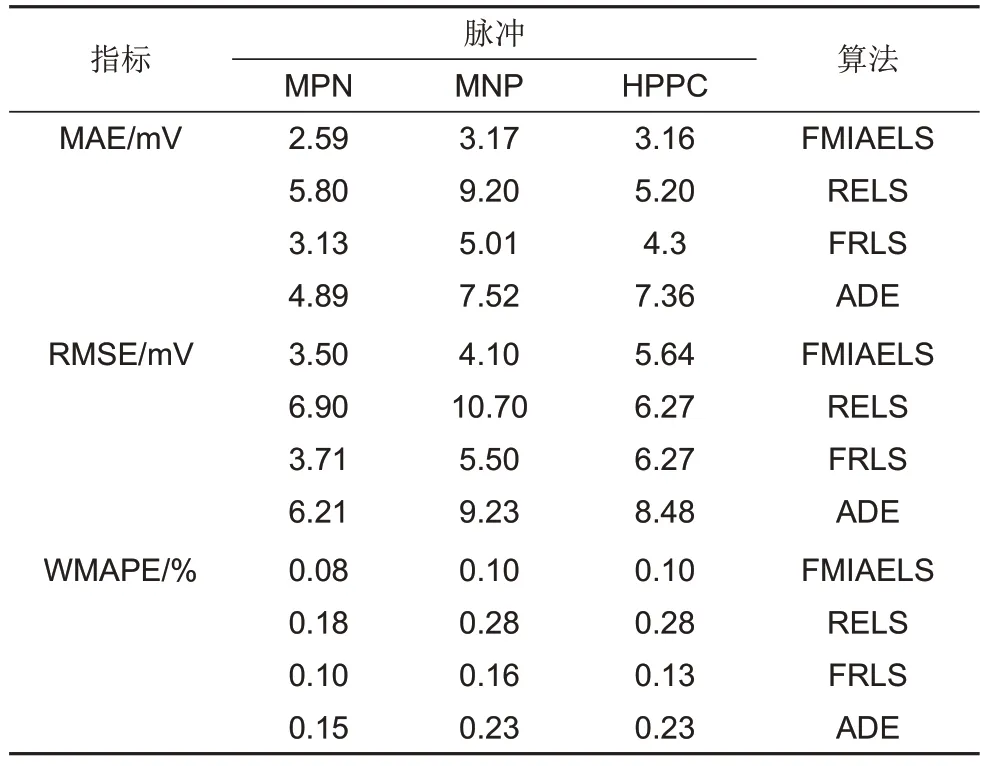
表4 一阶RC等效电路模型的仿真误差Table 4 Simulation error of the 1-order RC equivalent circuit model

4.2 测试工况下的仿真结果

为了进一步说明FMIAELS 在电池模型参数辨识方面的优势，在不同温度、测试工况及老化程度下，对FMIAELS、RELS和FRLS的仿真结果进行了对比说明。图7～图9 展示了在5 ℃、10 ℃和35 ℃的温度下，FMIAELS 和常用的系统辨识算法辨识的模型参数仿真的不同工况下端电压的误差。由图7～图9可知，FMIAELS在不同温度和测试工况下辨识的模型参数都能准确地模拟电池的特性。例如在5 ℃和35 ℃的温度中，FMIAELS的误差明显小于RELS和FRLS。

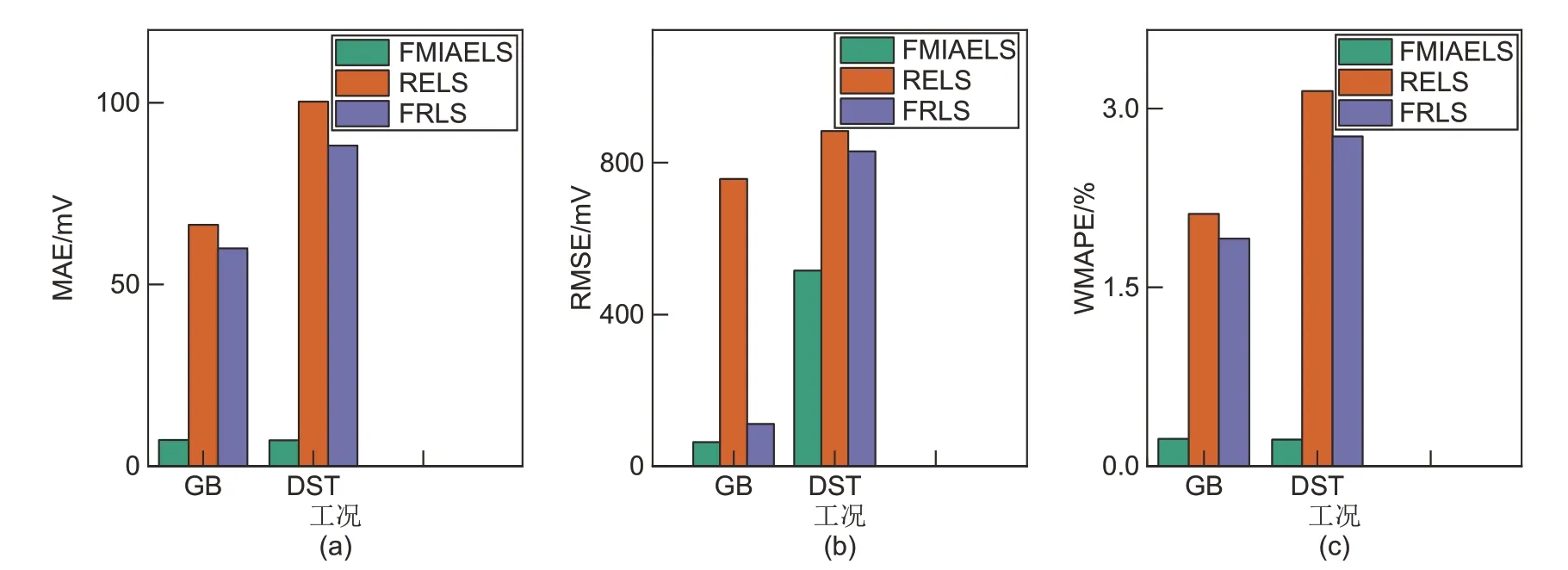
图7 不同工况下，FMIAELS、RELS和FRLS的误差(5 ℃)Fig.7 The error of the FMIAELS, RELS, and FRLS under different working conditions (5 ℃)

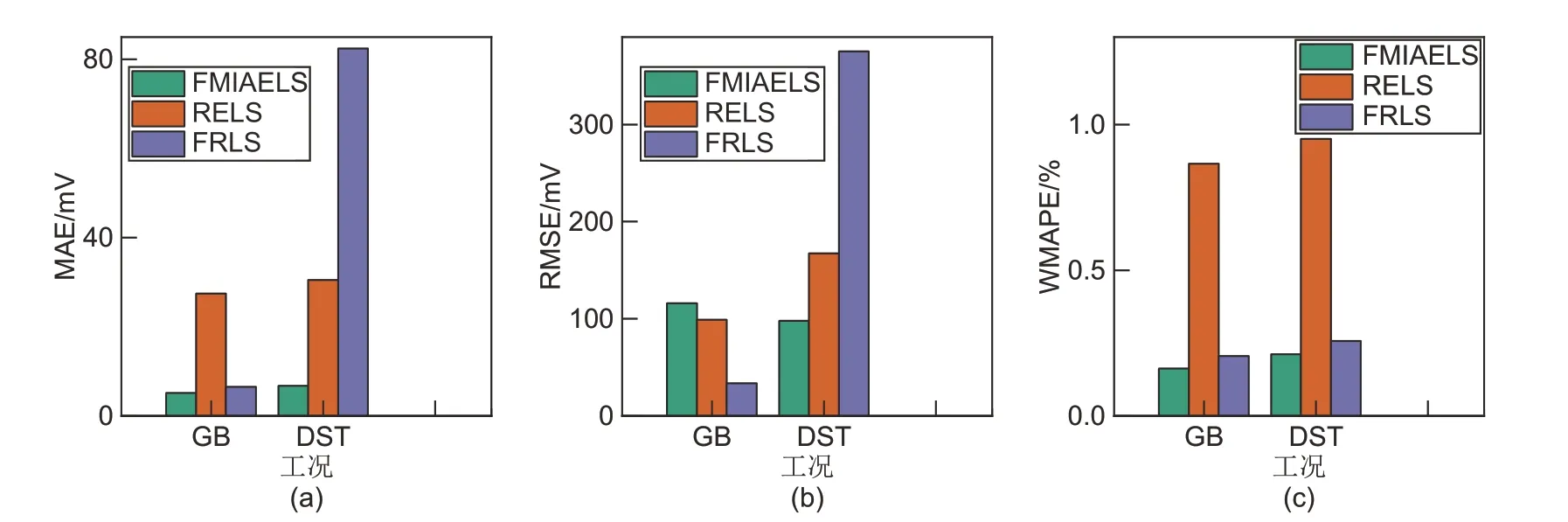
图8 不同工况下，FMIAELS、RELS和FRLS的误差(10 ℃)Fig.8 The error of the FMIAELS, RELS, and FRLS under different working conditions (10 ℃)

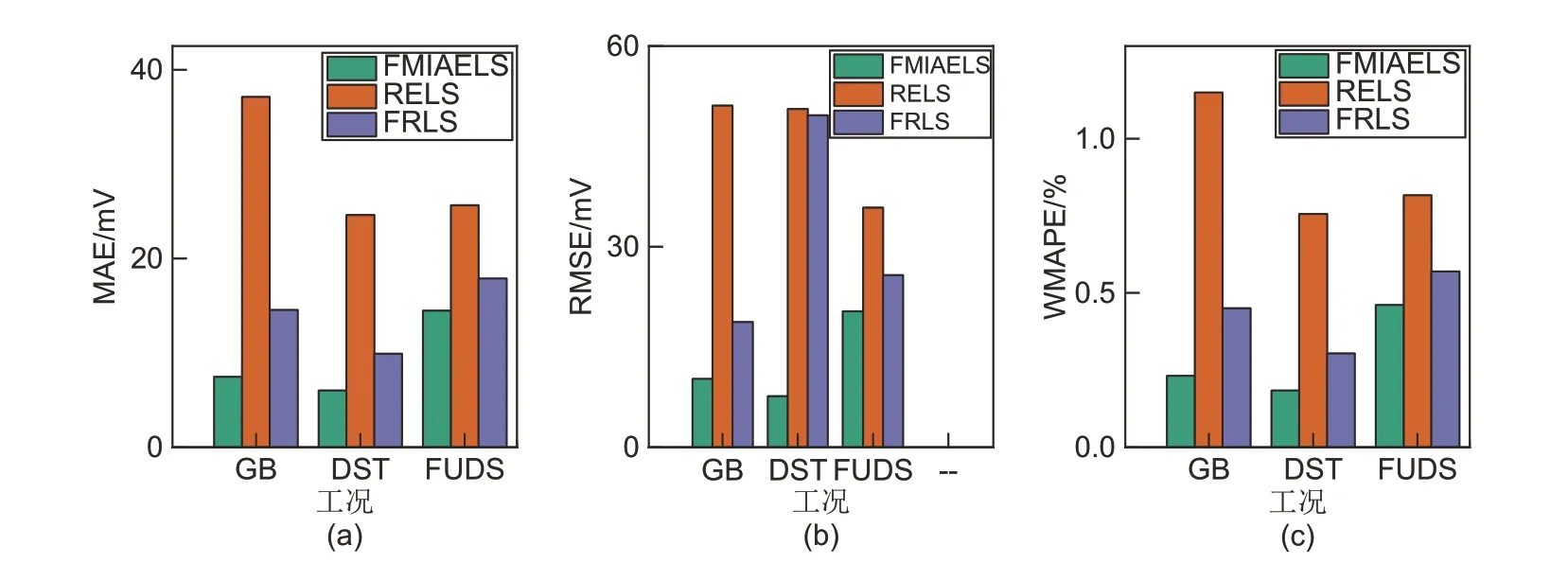
图9 不同工况下，FMIAELS、RELS和FRLS的误差(35 ℃)Fig.9 The error of the FMIAELS, RELS, and FRLS under different working conditions (35 ℃)

在不同的老化程度和测试工况下，如图10 和图11 所示，FMIAELS 的辨识精度依然高于RELS和FRLS。

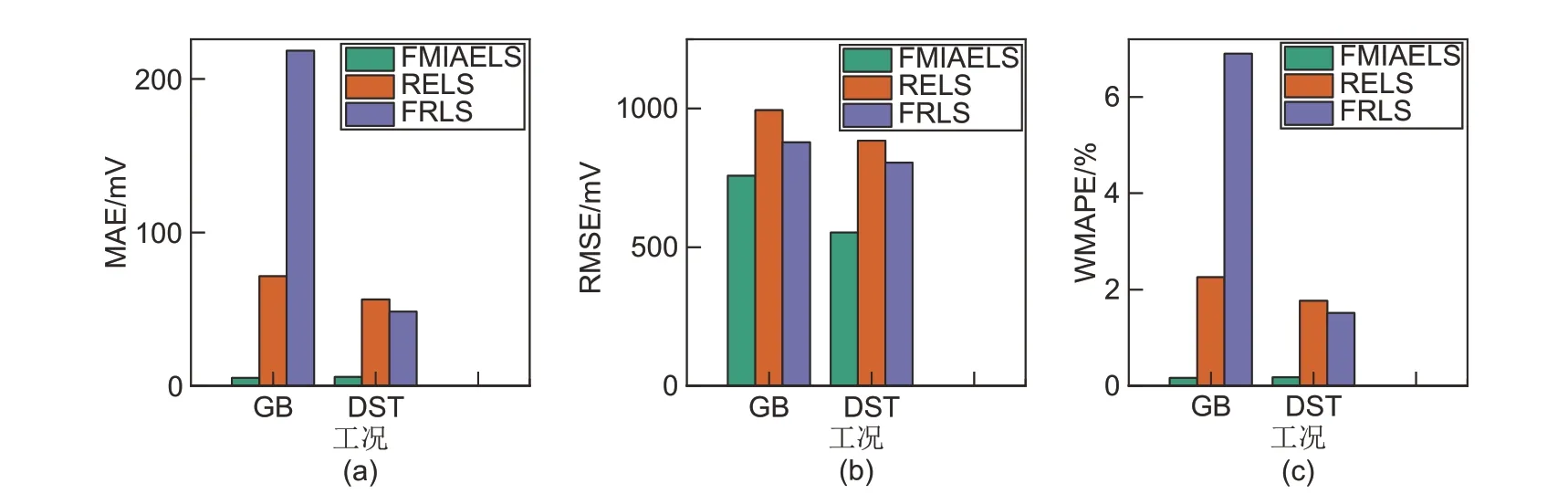
图10 不同工况下，FMIAELS、RELS和FRLS的误差(SOH=0.869，25 ℃)Fig.10 The error of the FMIAELS, RELS, and FRLS under different working conditions (SOH=0.869, 25 ℃)

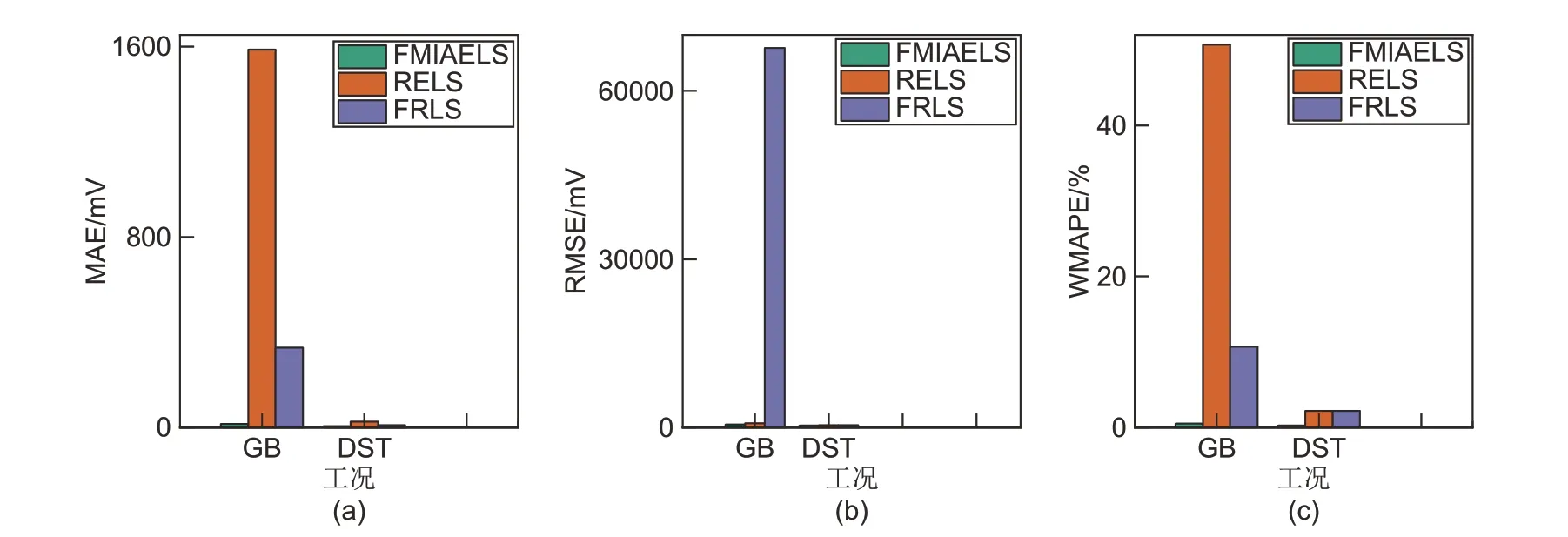
图11 不同工况下，FMIAELS、RELS和FRLS的误差(SOH=0.554，25 ℃)Fig.11 The error of the FMIAELS, RELS, and FRLS under different working conditions (SOH=0.554, 25 ℃)

总之，FMIAELS 比常用的系统辨识算法更适合不同温度、不同工况和不同SOH(State of health，动力电池健康状态)下的高精度模型参数辨识。

综合4.1 节和4.2 节的结果，本文提出的FMIAELS非常适合等效电路辨识模型的参数辨识，其辨识精度高于常用的系统辨识算法。

4.3 二阶RC等效电路模型参数的辨识结果

4.3.1 参数辨识结果根据FMIAELS 的辨识结果可分析二阶RC 等效电路模型参数的变化特性。由图12 和图13 可知，在相同的脉冲作用下，OCV、Ro、Rp1、Rp2、tp1和tp2随着脉冲作用时间的累积而逐渐变化，说明电池的模型参数受SOC的影响，不同SOC点处的模型参数不同。无论是在MPN脉冲、MNP脉冲还是HPPC脉冲作用下，前20 s的模型参数与后20 s的参数不相同，说明电池的模型参数也受电流倍率的影响。MPN 脉冲和MNP 脉冲的脉冲方向不同，此时电池的模型参数也不同(图13)，说明充电态与放电态的模型参数存在差异。

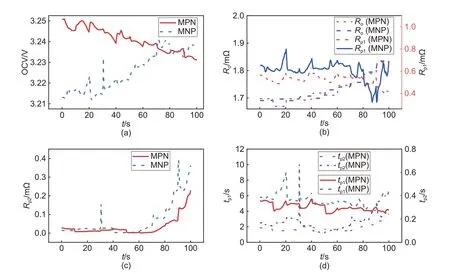
图12 FMIAELS在MPN脉冲和MNP脉冲下辨识的 (a) OCV、(b) Ro和Rp1、(c) Rp2及 (d) tp1和tp2Fig.12 (a) OCV, (b) Ro and Rp1, (c) Rp2 and (d) tp1 and tp2 identified by the FMIAELS under the MPN pulse and MNP pulse

4.3.2 OCV的辨识精度

为了评价OCV的辨识精度，利用静置1 h的方法获得电池实际的OCV，并计算辨识的OCV 与实际OCV 的相对误差。由图14 可知，在MPN、MNP 和HPPC 脉 冲 下，FMIAELS 辨 识 的OCV 的误差(平均相对误差0.22%)低于RELS(0.36%)、FRLS(0.34%)、RSNA(6.34%)、MRAS(1.36%)和ADE(0.29%)，因此FMIAELS 辨识的OCV 的 精度优于其他算法。综合4.1节～4.3节可知，FMIAELS在电池模型参数辨识上更具优势。

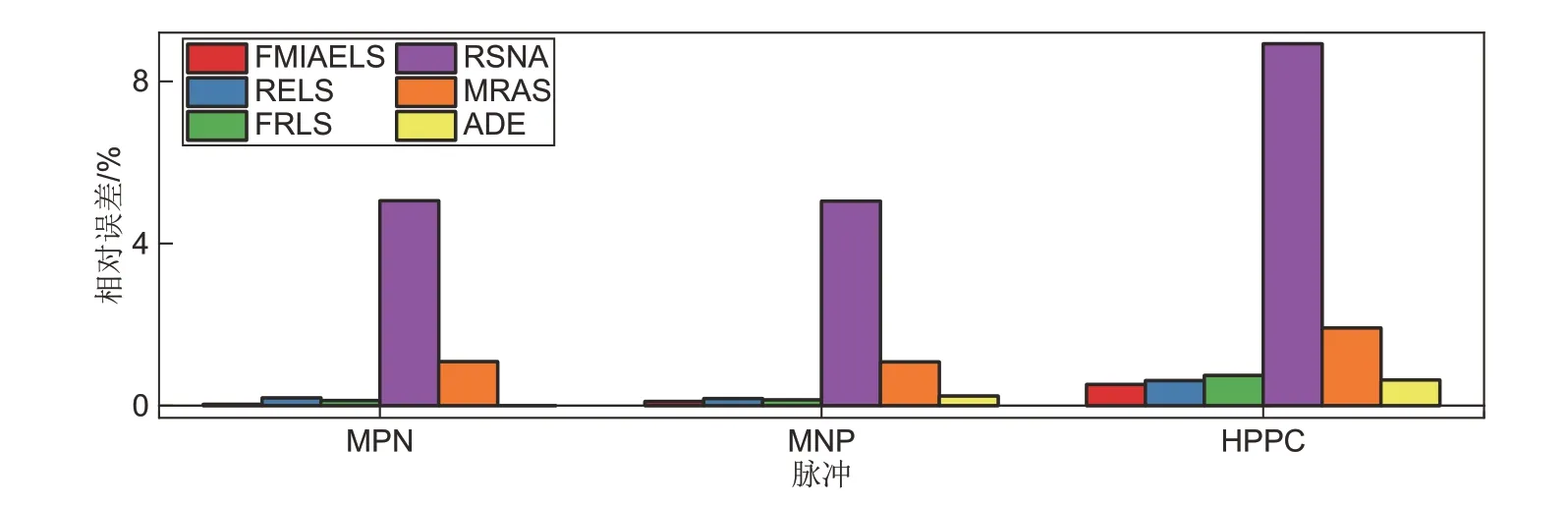
图14 OCV的相对误差Fig.14 Relative error of the OCV

4.4 辨识算法的特性

在给定的期望指标下，优化算法按照某些原则在指定的数据集中选择最佳的参数值，使得系统输出的性能指标达到最优。因此基于优化算法的等效电路模型参数辨识常会陷入局部最优状态，无法达到整体最优，而且无法实现实时的参数辨识。最小二乘一类的算法、RSNA算法和MRAS算法，虽然能够快速跟踪待估计的等效电路模型的参数，但存在收敛速度慢、估计精度低等缺点。这些算法都采用单一时刻的预报误差修正当前时刻的参数估计值，并忽略了大量有用的信息，导致这些算法存在鲁棒性差、精度低等问题。

FMIAELS将单一误差标量扩展为一个m维的误差向量(即多新息)，增益向量扩展为一个增益矩阵，利用多新息向量与增益矩阵校正新的参数估计值，加快了收敛速度，提高了辨识精度，鲁棒性也有较大提升。因此，FMIAELS的收敛速度和精度均明显优于RELS、FRLS、RSNA、MRAS和智能优化算法。

总之，电池为非线性系统，表现在模型上为时变参数的变化，因此二阶RC 等效电路模型的参数会受SOC、电流倍率和充放电状态的影响。获得精确的电池模型参数有利于提高电池状态估计的精度，本文提出的FMIAELS 能够准确辨识电池的模型参数，可进一步为容量和功率的估计奠定基础。

5 结 论

本文提出了统一的等效电路模型参数的辨识方程，实现了电池模型参数的在线及精确辨识。根据实验验证结果，主要的结论有：

（1）提出了可同时获得二阶RC 等效电路模型和PNGV模型参数的差分方程。

（2）结合多新息理论提出了FMIAELS 算法，实现了电池模型参数的实时、精确辨识。

（3）FMIAELS 非常适合等效电路模型的参数辨识，在不同温度、工况及老化程度下其辨识精度明显优于RELS、FRLS、RSNA、MRAS和智能优化算法，误差约为它们的1/3。

（4）FMIAELS在不同脉冲下辨识的OCV 的精度也明显优于RELS、FRLS、RSNA、MRAS和智能优化算法，平均误差仅有0.22%。

利用本文提出的等效电路模型的辨识方法和FMIAELS能够获得准确的二阶RC等效电路模型和PNGV模型的参数，可进一步研究电池状态的估计。

附录 FMIAELS算法的推导过程

由于采样系统存在噪声，对于1.3 节中电池模型的差分方程有如下形式：

式中，ϕs为系统的输入与输出的信息向量；θs为系统的待辨识参数；ϕn为有色噪声信息向量，ϕn=[vj-1…vj-d]T；θn为有色噪声的待辨识系数；vj为噪声。

若将系统的参数向量定义为θj=[θs,j θn,j]T，则信息向量可表示为ϕj=[ϕs,j ϕn,j]T，进而有：

式(A2)包含了未知变量，为了能够直接使用式(A2)，需要构造一个辅助模型：

式中，ϕa,j为辅助模型输入与输出的信息向量；θa,j为辅助模型的参数向量。

根据多新息系统辨识理论，需要将误差标量(即单一新息)扩展成误差向量(即多新息)。考虑jm+1 时刻到j时刻的新息，则系统的输出向量Ym,j、信息矩阵Φm,j及噪声向量Vm,j，可由如下定义：

根据式(A2)有：

准则函数可表示为：

对式(A8)求极小值，并借助辅助模型辨识方法，即可得到多新息辅助模型递推最小二乘算法(multi-innovation auxiliary model extended recursive least squares algorithm，MIAELS)，该算法可由式(A9)表示。

由于该算法对于所有的信息都按平等对待，新数据所提供的信息随着数据的增多而作用减小，使得该算法失去了实时跟踪时变系统参数的能力。若将遗忘因子η(0 ＜η＜1)引入式(A9)中，按加权的方式提高新信息在辨识方法中的作用，即可实现时变系统参数的实时辨识。因此，带遗忘因子的多新息辅助模型扩展递推最小二乘算法(multiinnovation auxiliary model extended recursive least squares algorithm with forgetting factor，FMIAELS)可表示为：

综合各种脉冲工况的辨识精度和实时性，本文所选m=10，η=0.9987。