考虑频率特性及储能电池状态的电化学储能参与一次调频控制策略

曹 钰，姜 彤，刘 炽，杨 勇，刘文飞，刘文颖

（1新能源电力系统国家重点实验室（华北电力大学），北京 102206；2国网甘肃省电力公司电力科学研究院，甘肃 兰州 730070）

在“双碳”目标的背景下，我国新能源发电再度进入发展快车道，大量新能源并网严重影响了电力系统的频率稳定性[1]。电池储能系统(battery energy storage system，BESS)由于具有响应速度快、调节精度高、可双向调节的特点，很好地契合了新能源渗透率不断增高的新型电力系统的频率调节需求。

目前，电化学储能参与一次调频主要采用虚拟惯性控制和虚拟下垂控制，二者分别对应频率变化率和频率偏差值敏感，前者可以快速支撑系统频率，后者可以有效减少频率变化量。设定临界值切换两种控制模式，可以发挥二者的控制优势，但两种控制模式切换时可能会造成储能出力的跃变，导致频率波动[2]。同时，基于固定阈值设置的切换临界值难以适应不同情况下的频率波动。文献[3]和文献[4]提出基于频率最大偏差值的切换临界值设定方法，但未考虑切换时的频率波动。文献[5]以频率变化率的正负为切换判据，配合死区，可以减少控制的切换次数，进而减少了功率跃动。文献[6]提出了考虑频率偏差及变化率的自适应控制方法，实现了两种控制模式的自适应组合，但未考虑频率恢复阶段虚拟惯性控制对频率恢复的阻碍作用。

大规模BESS 通常由多个储能单元构成[7]。随着储能电站投入使用时间的增加，各个储能单元电池的健康状态(state of health，SOH)逐渐产生差异，相同批次型号的锂电池SOH 极差可达到25%[8]。各储能单元SOH的差异将导致储能电池整体的性能大幅度衰减。SOH 的差异还会带来电池荷电状态(state of charge，SOC)的不一致，部分单体电池会偏离平均SOC，呈现“扫帚”效应，降低储能电站的可用充放电容量，进一步加剧各储能单元电池SOH 的差异，最终导致储能系统的容量及预期寿命严重降低。在储能电站进行有功调节时，针对电池状态的功率分配将有效缓解各个储能单元SOC及SOH的不一致性。文献[9]通过可变区间窗的方法，均衡电池组的SOC，但未考虑电池组的SOH。文献[10]根据电池状态确定了电池组的动作顺序，并根据SOH 修正储能虚拟下垂控制系数。文献[11]利用自适应变异粒子群优化算法，提出了考虑储能单元SOH 和SOC 一致性的BESS 功率分配策略，但由于算法较复杂，难以应用在一次调频时间尺度上的功率分配。综上，各学者对于电化学储能参与一次调频的两种控制模式平滑调节研究不够深入，对于储能参与调频时，各储能单元的SOH及SOC不均衡的问题关注较少。

本文主要研究了采用锂离子电池的储能电站参与一次调频的控制策略，首先分析了储能电站参与系统一次调频的控制模型；其次，基于频率特征采用模糊控制方法，提出了储能控制模式自适应调节方法；再次，通过SOH 对储能单元进行分组，基于各电池组SOC及SOH提出了储能单元出力分配方法；基于此，提出了考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制策略；最后，通过仿真试验验证了所提策略的有效性和可行性。

1 储能电站参与系统一次调频的控制模型

储能电站主要通过电池向电网输出或吸收功率来达到对电网频率调整的目的。图1为储能电站并网示意图。

图1 储能电站并网示意图Fig.1 Schematic diagram of grid-connected energy storage power station

由图1可知，储能电站的电池系统往往由多组储能单元共同构成，各储能单元通过储能变流器(power convert system，PCS)及变压器接入电网。当系统中负荷和新能源机组出力发生波动时，储能电站会和电网内的传统机组共同参与一次调频，进而将系统频率调整至一个稳定的值，储能电站参与系统一次调频的模型如图2所示。

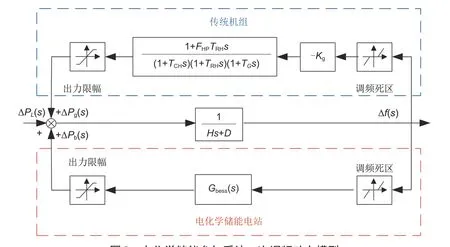
图2 电化学储能参与系统一次调频动态模型Fig.2 Dynamic model of primary frequency regulation of electrochemical energy storage participation system

图2 中，H和D分别为系统的惯性常数和阻尼系数；ΔPL(s)为系统内风、光波动和负荷变化造成的综合功率扰动；ΔPg(s)、ΔPb(s)分别是传统机组及电化学储能电站的有功出力变化量；Kg为传统机组的功率调节系数；TCH为汽轮机时间常数；TRH为再热器时间常数；FRH为再热器增益；TG为调速器时间常数；Gbess(s)为储能电站的调频传递函数；Δf(s)是系统的频率偏差。为了发挥储能电站快速响应的优势，增加储能电站参与一次调频的调节精度，设置储能电站调频死区阈值小于传统机组调频死区阈值。当Δf(s)超出储能电站调频死区时，储能电站根据Gbess(s)输出功率参与系统调频；当Δf(s)超出传统机组调频死区时，传统机组通过调速器改变汽轮机的输出功率参与调频，进而减少系统频率偏差。

当频率变化在死区范围外且各机组处于出力限幅内时，根据图2可以得到与频率变化量相关的方程组：

储能电站主要采用虚拟下垂控制和虚拟惯性控制参与系统调频，其传递函数为：

式中，Gbess1(s)、Gbess2(s)分别为虚拟下垂控制和虚拟惯性控制下储能电站的传递函数；Tb为储能电站的时间常数；Kb、Mb分别为虚拟下垂和虚拟惯性的功率调节系数。

根据式(2)可以看出，虚拟下垂控制主要是抑制系统的频率偏差，而虚拟惯性控制主要是针对系统的频率变化率进行控制，可以抑制频率的变化。两种策略对于频率的控制效果各有优劣，Gbess(s)中需要设计控制器针对频率特性进行控制模式的自适应调节。同时，Gbess(s)还需要综合各储能单元的电池健康状态及荷电状态对储能电站的输出功率进行合理分配。

2 储能电站参与系统一次调频的控制方法

2.1 基于频率特征与模糊控制的储能控制模式自适应调节方法

当电网负荷增加或新能源机组出力减少时，系统频率会出现波动，系统内具有调频能力的机组会参与一次调频，图3为一次调频频率特性曲线。

图3 一次调频频率特性曲线Fig.3 Frequency characteristic curve of primary FM

根据图3可以看出，系统主要经过t0～t1时间段的频率下降阶段和t1～ts时间段的频率恢复阶段。

在频率下降阶段，|dΔf/dt|在t0时刻达到最大，随后逐渐减小，直到t1时刻降为0，在此期间，Δf不断下降，在t1时刻达到-Δfmax。在频率下降阶段的初期，|Δf|很小，而|dΔf/dt|很大，此时储能电站应主要采用虚拟惯性控制抑制频率变化；在频率下降阶段的后期，系统|Δf|很大，而|dΔf/dt|很小，此时储能电站应主要采用虚拟下垂控制减小Δfmax。

在频率恢复阶段，Δf在t1时刻达到谷值，随后频率逐渐恢复，直到ts时刻稳定；dΔf/dt先上升后下降，在ts时刻稳定为0。在频率恢复阶段，储能电站应主要采用虚拟下垂控制助力频率恢复；由于在此期间，dΔf/dt为非负数，此时储能电站可采用“虚拟负惯性”控制加速频率的恢复。

根据频率在下降阶段和恢复阶段的不同特点，储能电站需要同时利用虚拟下垂控制和虚拟惯性控制的优势调节频率，为了避免两种控制切换造成储能电站出力的突变，本文采用模糊控制的方法调节两种控制模式的出力占比，综合两种控制模式同时进行一次调频。

模糊控制不依赖于控制对象的数学模型，可以模仿推理与决策过程对非线性系统进行智能控制，其控制方法主要包括模糊化、建立规则库、进行模糊推理和去模糊化。

首先进行问题的模糊化：设置模糊控制器输入系统频率变化量和频率变化率，输出量为虚拟下垂控制占比系数α和虚拟惯性控制占比系数β。根据电力系统正常运行条件下频率偏差限值的要求和高占比新能源电力系统的动态频率约束[12-13]，设置输入量频率变化量和频率变化率的论域分别为[-0.5,0.5]和[-1,1]。设置输出量α和β的论域分别为[0,1]和[-0.5,1]，利用三角形函数确定输入与输出直接的隶属度。输入变量划分为{NB,NM,NS,Z,PS,PM,PB}7个等级，分别表示输入变量的负向偏大(NB)、负向偏中(NM)、负向偏小(NS)、零(Z)、正向偏小(PS)、正向偏中(PM)、正向偏大(PB)状态；输出变量划分为{NM,NS,Z,S,M,L,VL}7个等级，分别表示输出变量的负向偏中(NM)、负向偏小(NS)、零(Z)、小(S)、中(M)、大(L)、非常大(VL)状态。

其次，建立规则库进行模糊推理，按照以下原则进行设置：

（1）当系统|Δf|很小，而|dΔf/dt|很大时，模糊控制虚拟下垂控制系数取小值，虚拟惯性控制系数取大值；

（2）当|Δf|很大，而|dΔf/dt|很小时，模糊控制虚拟下垂控制系数取大值，虚拟惯性控制系数取小值；

（3）当Δf和dΔf/dt不同号时，模糊控制虚拟惯性控制系数取负值，助力频率恢复。

根据上述原则进行设置后的规则如表1 和表2所示。最后，利用重心法对控制量进行去模糊化，得到如下的模糊控制对应曲面，如图4所示。

表1 虚拟下垂控制占比系数α模糊规则表Table 1 Virtual sag control occupancy factor α fuzzy rule table

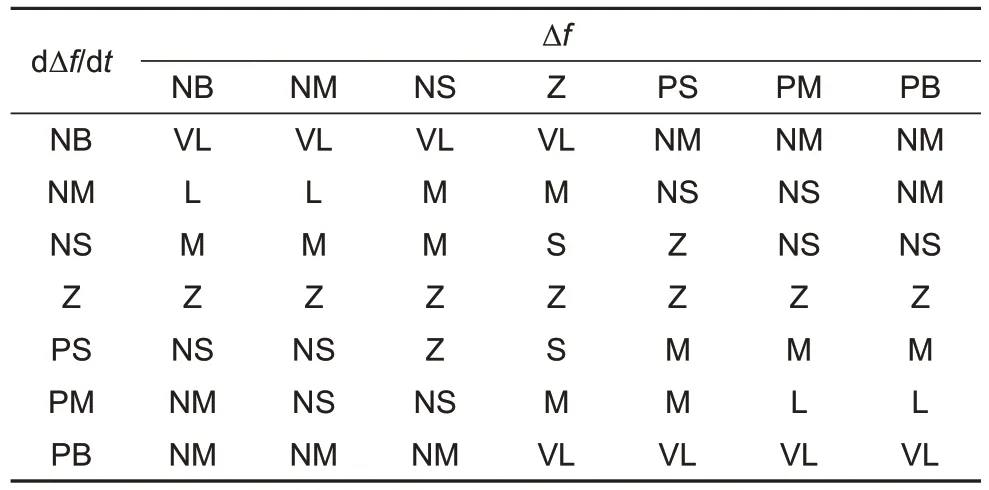
表2 虚拟惯性控制占比系数β模糊规则表Table 2 Virtual inertia control occupancy factor β fuzzy rule table

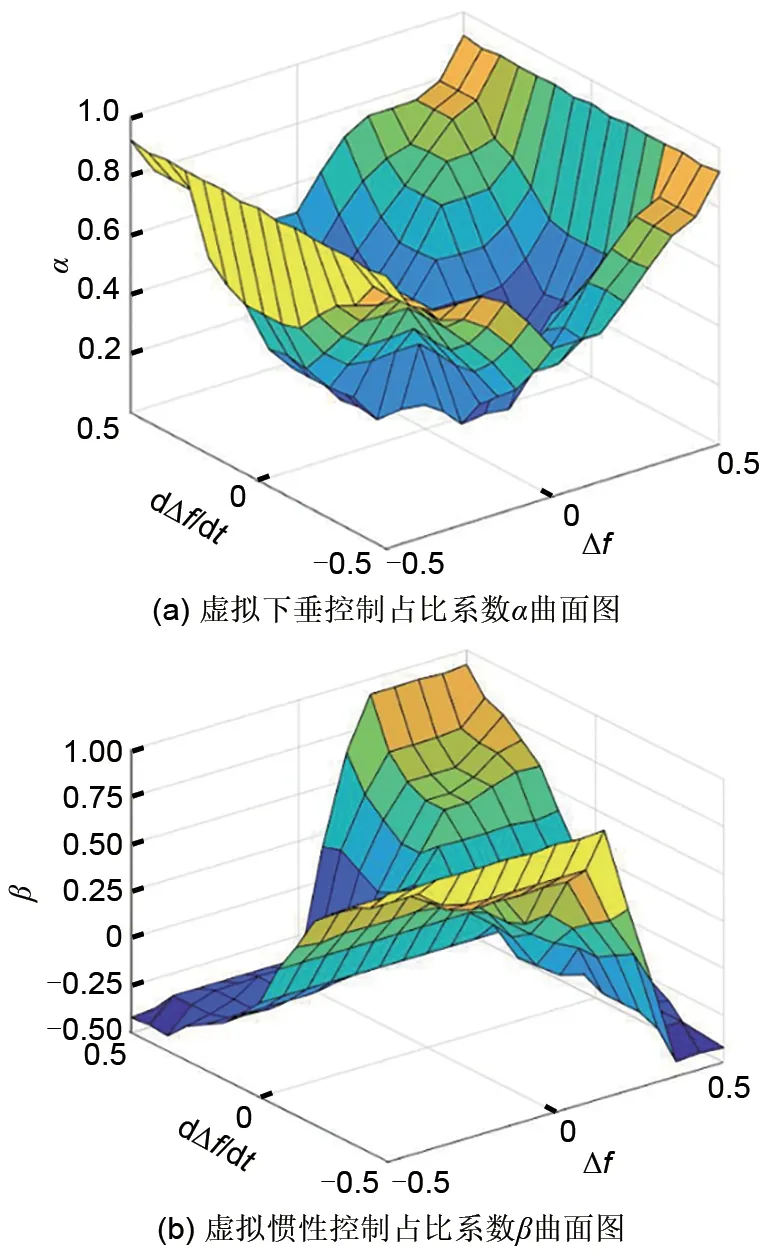
图4 模糊控制对应曲面图Fig.4 Fuzzy control corresponds to surface diagram

结合式(2)可以设置储能电站输出的有功功率变化量为：

式中，ΔPbess1为储能电站虚拟下垂出力；ΔPbess2为储能电站虚拟惯性出力。

2.2 基于储能单元SOH及SOC的出力分配方法

根据式(3)可以得到储能电站参与一次调频的出力，本节将结合储能电站储能单元的SOC 及SOH 对各储能单元的输出功率进行分配。已知SOH满足下式[14]：

式中，Qaged为锂电池在当前状态下的最大容量；Qnew为未投入使用的新电池的额定容量。投入使用的锂电池SOH 在80%～100%之间，且SOH与锂离子电池的放电深度强相关[15-17]。

由于储能单元电池的SOH 无法直接测得，且电池容量衰退主要受循环次数的影响，故可每24 h采用基于数据驱动的方法对各储能单元电池的SOH进行在线估计[16]。接下来，对储能电站内储能单元的SOH进行排序，按照SOH从低到高分为电池组Ⅰ、Ⅱ、Ⅲ、Ⅳ 4组：其中，Ⅰ组内电池SOH最差，Ⅳ组内电池SOH 最好。为保证储能电站电池系统整体的寿命及健康状态，本文设置SOH 差的电池组Ⅰ少动、浅动，电池组Ⅳ多动、深动。每个电池组的输出功率为：

式中，Pb(i)为第i组电池组的出力；μi为第i组电池组的出力系数；f(SOHi，SOCi)为第i组电池组的SOH和SOC相关的函数；Pb为储能电站的输出功率，满足。

设置电池组i的输出功率占比系数为Rb(i)，则有：

各储能单元的功率分配主要在于f(SOHi,SOCi)的设计，为保证储能参与系统频率调节的响应速度，f(SOHi,SOCi)应具有能够快速运算的特性。

首先，对各电池组的功率根据SOH进行分配。参照式(4)，按照健康状态好的电池组多动、深动，健康状态差的电池组少动、浅动的原则设置，设置输出功率占比系数与各电池组的SOH 呈正相关。由于各电池组SOH 间数值差异的数量级较小，为保证SOH 越好的电池组分配功率越多，SOH 越差的电池组分配功率越少，结合各电池组的序号，设置功率占比系数：

若只按照式(7)的占比对储能电站的功率进行分配会导致各电池组的SOC 差异明显增大，极易导致健康状态好的电池组动作深度过深，为了改善这一现象，接下来本文基于各电池组的SOC 对式(7)进行修正。

假设储能电站处于充电状态，同时考虑SOH及SOC的一致性，令

式中，η为与SOC相关的分配系数，其为非负数，η的大小决定了各电池组SOC趋于一致的速度。

根据上面的推导，各量满足如下关系：

式中，Pbmax为储能电站的功率上限值。

将式(9)进行变换可以得到：

式中，f(SOHb,SOCb)为电池储能电站电池组充电功率平均分配系数。

由于：

所以存在：

可知：

为保证各电池组SOC的偏差不过大，η取值为：

由此，第i个电池组的充电功率为：

同理，在放电状态下，第i个电池组的放电功率为：

2.3 考虑频率特性及储能电池状态的电化学储能

参与一次调频综合控制策略

综合基于频率特征的储能控制模式自适应调节和电池组SOH及SOC的出力分配策略，考虑到电池储能的容量限制及出力深度限制，得到考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制框图如图5所示。

图5 考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制框图Fig.5 Block diagram of integrated control of electrochemical energy storage participation in primary frequency regulation considering frequency characteristics and energy storage battery state

为了防止在某些储能电池组健康状态极差较大的情况下，健康状态好的电池组可能会出现的SOC 越限的问题，设置基于SOC 的功率分配死区和功率分配限制区域如图6所示。

图6 电池组功率分配区域Fig.6 Battery pack power distribution area

参照图6，当电池组处于[0，SOCmin]范围时，电池组不参与放电功率分配，当电池组处于[SOCmax，1]范围时，电池组不参与充电功率分配。当电池组处于(SOCmin，SOClow)范围时，令式(16)中分子的i=0，限制其放电功率分配，同理，当电池组处于(SOChigh，SOCmax)范围时，令式(15)中分子的i=0，限制其充电功率分配。考虑到有些储能电池可能存在温度过高/过低现象，或出现电池故障的特殊情况，本文在储能电站参与调频的功率分配前加入温度监测及故障监测环节。当电池温度高于工作高温阈值Tmax或低于低温阈值Tmin时，禁止此电池参与功率分配，当监测到某储能电池发生故障时，闭锁该电池的充放电功能。本文设定Tmax和Tmin分别为40 ℃和0 ℃[18]。

综上，考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制流程如图7所示。

图7 考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制流程图Fig.7 Considering the frequency characteristics and the state of the energy storage battery electrochemical energy storage involved in the integrated control flow chart of primary frequency regulation

3 算例分析

为了验证本文所提控制策略的可靠性和有效性，本文在MATLAB/Simulink平台上搭建仿真模型，其中，传统发电机组配置额定容量550 MW，系统的额定频率为50 Hz，系统内配有功率为60 MW的电池储能系统，为方便分析储能电站各电池组SOC 的变化过程，设置储能电站容量为15 MWh，设置储能电站调频死区为60%的常规机组调频死区，提高储能参与一次调频的调节精度，仿真模型的具体参数如表3所示。

表3 仿真模型参数Table 3 Simulation model parameters

仿真主要采用阶跃扰动和连续负荷扰动的工况来模拟新能源出力波动带来的频率波动。在频率调节效果方面，主要对比分析以下4种情况：①储能采取本文所提控制策略；②储能采用虚拟惯性控制和虚拟下垂控制直接切换控制；③储能仅采用下垂控制；④无储能参与调频。在储能电池的状态方面，本文将各电池组在本文控制策略和功率平均分配时电池的状态及循环区间进行了对比。储能电站各电池组的SOH 和初始SOC 如表4 所示，电池整体的SOH为0.9，SOC为0.6，取各电池组SOH分别为(0.9±0.02)和(0.9±0.04)。为了对比相同SOC下SOH 对于功率分配的影响，电池组Ⅰ和电池组Ⅳ初始SOC 相同，电池组Ⅱ和电池组Ⅲ初始SOC相同。

表4 储能电站各电池组的初始状态Table 4 The initial state of each battery pack of the energy storage plant

3.1 阶跃负荷扰动工况

仿真系统设定在1 s 时产生95 MW 的阶跃负荷，主要以频率最大偏差值Δfmax、频率偏差峰值到达时间tm和稳态频率偏差值Δfs作为频率调节的评价指标。同时，关注储能单元的SOC 及其循环区间。仿真的频率变化率曲线和储能电站的出力曲线如图8 和图9 所示。储能电站的频率调节指标数值如表5所示。

表5 阶跃负荷下储能电站的频率调节指标Table 5 Frequency regulation index of energy storage plant under step load

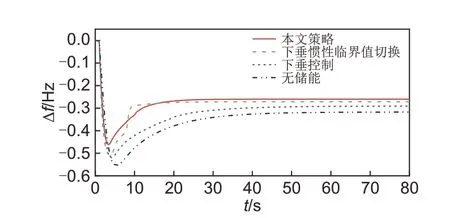
图8 频率偏差对比曲线Fig.8 Frequency deviation comparison curve

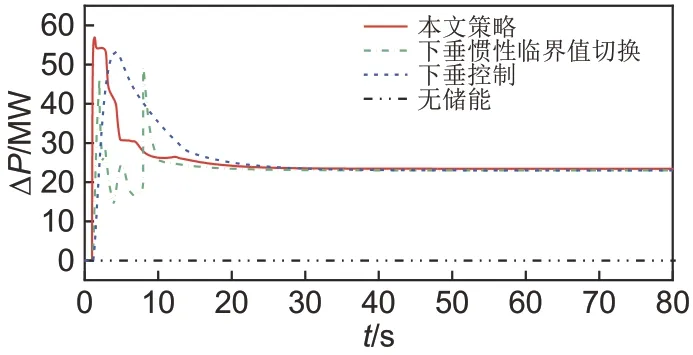
图9 储能出力对比曲线Fig.9 Energy storage output comparison curve

由图8、图9 及表5 可知，在频率下降初期，本文控制策略的储能出力能够根据频率特征快速响应，于1.4 s 达到出力峰值，并在后续过程中无明显功率跃变。同时，本文策略下频率调节指标较其他策略更好，频率偏差到达峰值的时间最短，频率偏差控制在±0.5 Hz 以内。可见，本文策略对于阶跃负荷扰动的响应速度快，频率偏差绝对值小。进行本文功率分配策略和平均功率分配的SOC变化如图10所示，其电池状态具体数值对比如表6所示。

表6 阶跃负荷下参与调频前后的储能电池组状态Table 6 The state of the energy storage battery pack before and after participating in frequency regulation under step load

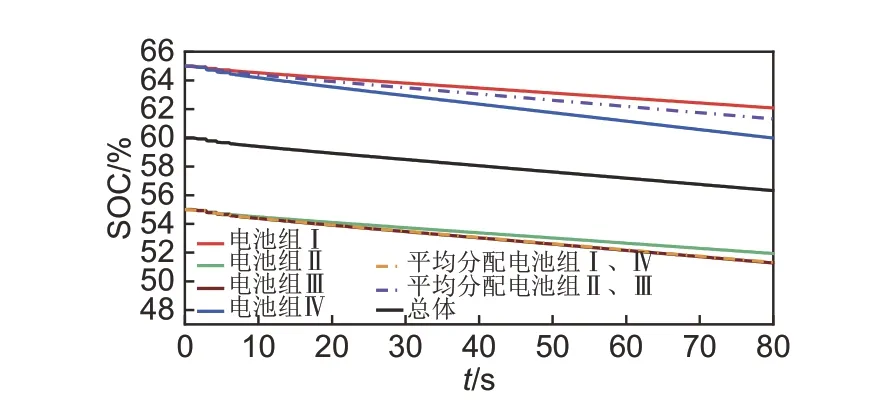
图10 阶跃负荷下储能电站各电池组SOC变化曲线Fig.10 SOC variation curve of each battery group in energy storage plant under step load

由图10和表6可知，在阶跃负荷扰动下，各电池组循环期间上限为SOC 初始值，在本文的分配策略下，SOH 较差的电池组，动作幅度和深度更小，SOH 好的电池组动作幅度更大，有助于保持储能电站电池SOH的一致性，增加其预期寿命。

3.2 连续负荷扰动工况

接下来设置连续负荷扰动，验证所提控制策略的有效性，本文设置20 min 的负荷扰动如图11 所示，其中负荷波动最大值为90 MW。本文主要以频率偏差峰谷差值fptov、频率偏差均方根Δfrms来判断调频效果。仿真的频率变化率曲线和储能电站的出力曲线如图12和图13所示。储能电站的频率调节指标数值如表7所示。

表7 连续负荷下储能电站的频率调节指标Table 7 Frequency regulation index of energy storage plant under continuous load

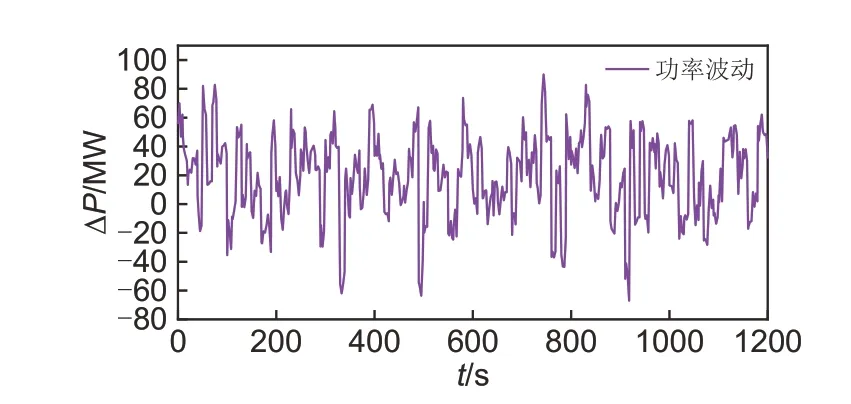
图11 连续负荷波动Fig.11 Continuous load fluctuation

图12 频率变化曲线Fig.12 Frequency change curve

图13 储能电站出力变化曲线Fig.13 Energy storage power plant output change curve

由频率变化曲线及频率调节指标可以看出，在本文所提控制策略下，频率波动范围更小，且频率偏离均值程度更小。储能电站参与一次调频，进行本文功率分配策略和平均功率分配的SOC 变化如图14所示，其状态具体数值对比如表8所示。

图14 连续负荷扰动下储能电站各电池组SOC变化曲线Fig.14 Change curve of SOC of each battery group in energy storage plant under continuous load disturbance

由此可知，在此连续负荷扰动下，储能电站放电出力总体上多于充电出力，调频过程中各电池组SOC最大值等于初始SOC。本文策略下，SOH好且SOC较高的电池组循环区间更大，而SOH差且SOC 较低的电池组循环区间较小，有助于减缓其电池组健康状态的衰减速度，提高整体储能系统的运行寿命。

4 结 论

针对新能源富集电力系统频率波动的问题，本文基于频率特征和模糊控制，提出了储能控制模式自适应调节方法；针对储能电站内部锂电池状态不一致问题，本文通过SOH 对储能单元进行分组，基于各电池组SOC及SOH提出了储能单元出力分配方法。综合上述方法，提出了考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制策略。最后，在阶跃负荷和连续负荷扰动工况下，搭建系统模型进行仿真，验证了考虑频率特性及储能电池状态的电化学储能参与一次调频综合控制策略的有效性和可行性。得到以下结论：

（1）在一次调频控制效果方面，在阶跃负荷扰动下，本文控制策略较虚拟下垂与虚拟惯性直接切换控制策略，最大频率偏差减少0.048 Hz，频率恢复时间减少0.344 s，在连续负荷扰动下，本文所提策略较虚拟下垂与虚拟惯性直接切换控制，频率偏差峰谷差值减少0.111 Hz，采用本文控制策略可以更好地基于频率的特征调整储能出力，减少频率偏差和频率变化率，减少频率恢复时间。

（2）在各电池组的状态方面，在本文算例中的20 min 连续负荷扰动下，具有相同初始SOC 时，SOH 低的电池组比SOH 高的电池组少放电2.38%(SOC)，循环区间更小，本文所提策略可以在储能电站调频时，有效减小健康状态差的储能电站的动作深度，提高储能电站内储能单元电池状态的一致性，提高储能电站电池的使用寿命。