基于三种机器学习算法广西冷湿天气预报对比研究∗

覃卫坚 史旭明 陆 虹 金 龙

（1.广西壮族自治区气候中心 南宁 530022）（2.桂林航天工业学院理学院 桂林 541004）

1 引言

广西冬季受冷空气南下影响，经常有持续的低温冰冻雨雪天气过程出现，严重地影响着人们的生活，如2008 年广西发生了历史罕见的低温冰冻雨雪灾害过程，使交通运输、电力输送、农业和林业生产受到了严重影响，直接经济损失高达321.75 亿元。提高冷湿天气预报准确率，让人们提前做好防备、减少灾害损失，成了迫切的社会需求。天气变化是一种非线性的大气运动过程，一些研究表明使用支持向量机、神经网络等机器学习算法能够很好地处理气象预报中的非线性问题和提高气象预报准确率，如史旭明等［1］、孔庆燕等［2］使用支持向量机学习算法在降水定量预报中应用，预报准确率高于数值模式预报；Tao 等［3］将混合支持向量机算法在长江流域降水预测中应用，预测效果好于经验分解模态和差分进化算法；Rasp and Lerch［4］使用神经网络机器学习方案提高了天气集合预报准确率；Zeng等［5］研究指出神经网络模型使环流预报可靠性可延长到4周；李晓岚等［6］指出BP人工神经网络方法可提高空气质量浓度预报准确率；陆虹等［7］、覃卫坚等［8］利用粒子群-神经网络分别建立了低温雨雪天气和寒露风日数预报模型，预报误差明显小于逐步回归方法；黄小燕和金龙［9］把遗传神经算法应用在台风路径预报中，发现其能够提高台风路径预报精度；陈文兵等［10］将深度卷积神经网络模型应用于浓雾天气预报中，取得了良好的预报效果。为了提高广西冷湿天气预报准确率，本研究利用适应度函数对惩罚参数、核函数参数、不敏感损失函数进行了优化，建立了支持向量回归模型；增加了冲量项的误差反向传播算法，使神经网络算法中步长不稳定性得到了改善；解码遗传种群中的遗传个体，计算得到遗传神经网络集合预报值，为广西冷湿天气预报提供参考。

2 资料与方法

2.1 资料来源

使用1951 年-2017 年12 月-2 月广西90 个地面气象观测站逐日气温、逐日降水量资料；1951年-2017 年NCEP/NCAR 2.5×2.5°格点的逐日高度场、风场、气温、相对湿度再分析资料。

2.2 研究方法

2.2.1 冬季冷湿指数

冷湿指数（PT）采用周秀华等［11］提出的计算公式：

式（1）中，Ti、Pi分别为冷湿天气过程第i天平均气温和降水量；Tˉ、Pˉ分别为同一时间段历史平均气温和降水量；Ts、Ps分别为同一时间段历史气温和降水量标准差。PT值越大，天气冷湿程度越严重；PT值越小，天气冷湿程度越轻。

2.2.2 支持向量回归模型方法

支持向量回归模型方法（Support Vector Regression，SVR）是在处理非线性问题中，将低维样本空间非线性数据集通过核函数映射到高维的Hilbert 特征空间，把非线性问题化为线性问题，再通过回归方法进行估算，最后得到最优解［12］。

设定训练样本集T={xi,yi,i=1,2,…,n} ，其中xi∊Rd为输入值，yi∊R为目标值。样本非线性数据集通过φ(.)函数映射到线性高维的Hilbert 特征空间，构建回归估算函数：

式（2）中，ω∊Rd；b∊R。

以下通过使用不敏感损失函数ε求解ω和b：

在求解以下最小化目标函数过程中依据了结构风险最小化原则，结果相当于得到了式（2）的拟合［13］：

式（4）中，C 为惩罚参数；ξi-与ξi+为松弛变量。将式（4）进行拉格朗日变换，得到其对偶问题［14］：

式（5）中，核函数使用了径向基函数：B(xi,xj)=exp{- (xi-xj)2/(2σ2)} ，通过计算求得最优拉格朗日乘子ai和a*i；支持向量为(ai-a*i)≠0 的训练样本，支持向量数为S。在计算过程中利用适应函数对惩罚参数、核函数参数、不敏感损失函数进行了优化，最后得到回归函数：

2.2.3 冲量项神经网络模型

误差反向传播（Back Propagation，BP）算法是利用梯度算法迭代来求解权值，即把样本输入输出转变为没有约束的非线性最优化计算。BP 算法在学习过程中受步长η大小的影响很大；如果步长η值过大，那么计算收敛快，可能引起不稳定，在计算过程中权值超出某一个误差的极小值，呈不规则的波动，而导致不收敛；如果步长η值过小，那么计算收敛慢，学习时间过长，难于得到最优解。针对BP算法的这些问题，增加冲量项改进BP 算法能够比较合理地调节学习过程中步长η值，向着底部平均方向发展，从而使波动减少，起到缓冲平滑作用，提高了BP算法调整各层权值的审计网络学习效率及其自适应能力［15］。增加冲量项的BP算法调整网络的隐含层和输出层权系数的计算公式为

式（7）中，ω(k)为第k 个时间点独个的连接权系数或连接权向量；D(k)=∂J/∂ω(k)，为第k 时间点的负梯度；D(k-1)为第k-1 时间的负梯度；η为步长值，η>0；a为动量项因子，0 ≤a<1。

2.2.4 遗传神经网络模型

遗传算法是由Holland（1975年）提出的基于生物遗传规律的智能全局优化搜索算法［16］，近年来在气象等领域得到了应用，并取得良好的效果［17~18］。以下遗传神经网络模型使用二进制和实数混合编码方法，基本模型采用三层BP神经网络，将各层节点、连接权、阀值按顺序排列成一串，作为一个遗传神经网络预报模型的遗传个体［19］。

1）适应度函数计算

（1）对遗传种群中遗传个体进行解码，得到其隐节点、连接权，输入训练样本计算得到隐层输

出［20］：

式（8）中，vki为输入层到隐层的连接权系数矩阵；θi为相对应的阀值。

（2）然后计算从隐层到计算网络输出：

式（9）中，wij为隐层到网络输出层的连接权系数矩阵；ςj为相对应的阀值；f为转移函数。

（3）计算网络总误差为

从而得到适应度函数：

式（10）~式（11）中，n为训练集的样本数量。

2）进化操作过程

依据遗传个体的适应度对遗传种群作进化操作，使用选择、交叉和变异三个遗传算子，经过进化计算得到新一代遗传种群。

（1）选择算子使用轮盘选择方法，计算每一个遗传个体被选中的概率［21］为

式（12）中，Fi(x)为第i 个遗传个体的适应度；m 为种群的遗传个体总数；这样大概率保证适应度大的个体能够遗传到下一代。

（2）交叉算子是依据交叉概率Pi随机设置遗传个体编码串中的多个交叉点，并进行基因交换，得到新的遗传个体。

（3）变异算子是依据概率Pm开展遗传个体与其它遗传个体进行基因对位替换，形成新的遗传个体。

反复进行以上三个算子的进化操作计算，直到进化到N代，计算结束。解码遗传种群中每一个遗传个体，得到m 个神经网络的连接权和隐节点，作为集合预报个体成员，建立集合预报模型，计算得到遗传神经网络集合预报值。

3 结果分析

3.1 预报因子的普查和筛选

利用式（1）计算得到广西1951年-2016年冷湿天气过程的PT 值，计算PT 值与前一天NCEP/NCAR 高度场、风场等再分析资料的相关系数，得到了显著相关的区域，计算相关显著区域格点的平均值作为预选因子，将临近的、相关符号相反的因子的格点平均值相减作为组合因子，经过这样处理后能够显著地提高因子与冷湿指数的相关程度。按相关系数从高到低排序进行初步筛选，得到了42 个预报因子。为了尽量避免不良因子的相互干扰，剔除重复因子，选择有重要作用的因子，使用逐步回归方法做进一步筛选，而且重点考虑造成区域持续性低温雨雪事件有关的、物理意义较明确的因子能够进入预报模型。取F=5，建立了广西冷湿天气逐步回归预报方程：

式中，x14、x17、x22、x23、x25、x36为入选的预报因子，利用这6 个预报因子和114 个建模样本，分别采用支持向量机回归、冲量项神经网络以及遗传神经网络三种机器学习算法进行预报建模。x14为北太平洋中部与日本附近区域700hPa 气温之差；x17为华南地区上空500hPa 湿度与热带西北太平洋相减，反映了西北太平洋热带天气系统对广西的影响；x22为菲律宾以东洋面上空925hPa 湿度与中国东部之差，反映了西北太平洋热带系统对中国东部低层水汽活动的影响；x23为西伯利亚北部地区与贝加尔湖—巴尔喀什湖一带上空200hPa 纬向风之差；x25为伊朗高原700hPa 纬向风与贝加尔湖—巴尔喀什湖一带相减；x36为北太平洋中部与千岛群岛附近上空500hPa 高度场之差，表现出了高纬度地区环流波动信号。

3.2 逐步回归方法预报

首先使用传统的逐步回归方法来进行预报试验，独立样本数为10，在进行独立样本预报时，使用前一天NCEP 再分析实况场，计算得到6 个预报因子资料，并代入式（13），计算得到24h 逐步回归方法冷湿指数预报值，误差平均为-5.31，即预报平均值小于实况值，预报平均相对误差为26.94%（如表1）。

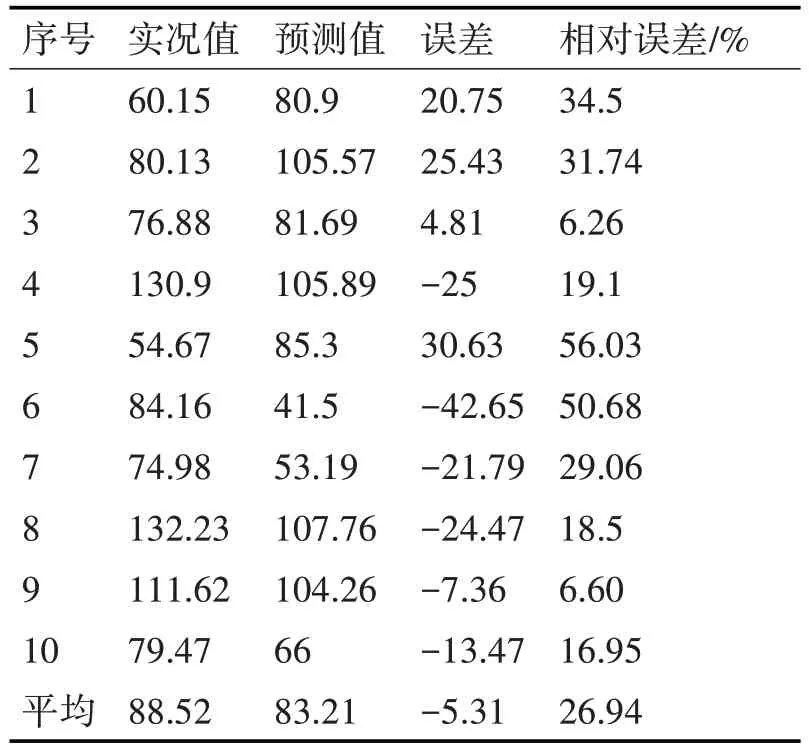
表1 2017年广西冷湿天气逐步回归预报方法预报结果

3.3 支持向量回归模型（SVR）预报

支持向量回归模型各参数设置为最大进化代数为100，种群个数为50，变异概率为0.5，交叉概率为0.9，拉格朗日乘子上界C∈［0，300］，高斯核函数的宽度б∈［0，2］，不敏感损失函数的参数ε∈［0，0.3］。支持向量回归模型的建模样本个数为114，预报因子为6 个，独立预报样本数为10，使用前一天NCEP 再分析实况场，计算得到预报因子资料，预报模型拟合平均误差为22.78。从支持向量回归模型10 个独立预报样本的预报检验结果来看（见表2），预报值平均为85.23，与实况误差平均为-3.29，预报值总体比实况平均值偏小，平均相对误差为22.58%，较逐步回归方法减小了4.36%。

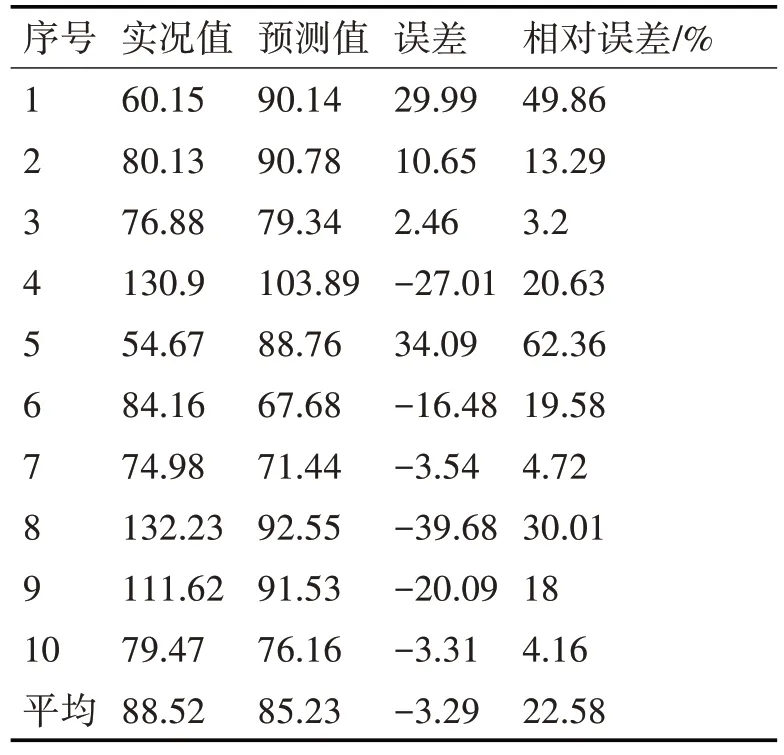
表2 2017年广西冷湿天气支持向量回归模型（SVM）预报结果

3.4 冲量项神经网络模型预报

冲量项神经网络模型参数设置为隐接点为3个，训练最多为1000 次，目标误差为0.01，学习速率为0.9，动量因子为0.75。冲量项神经网络模型的建模样本为114 个，预报模型拟合误差为13.68。从冲量项神经网络模型10个独立预报样本的预报结果来看，预报平均值为95.72，与实况误差平均为7.2，预报平均值高于实况平均值，相对误差平均为25.04%，较逐步回归方法减小了1.9%（表3）。

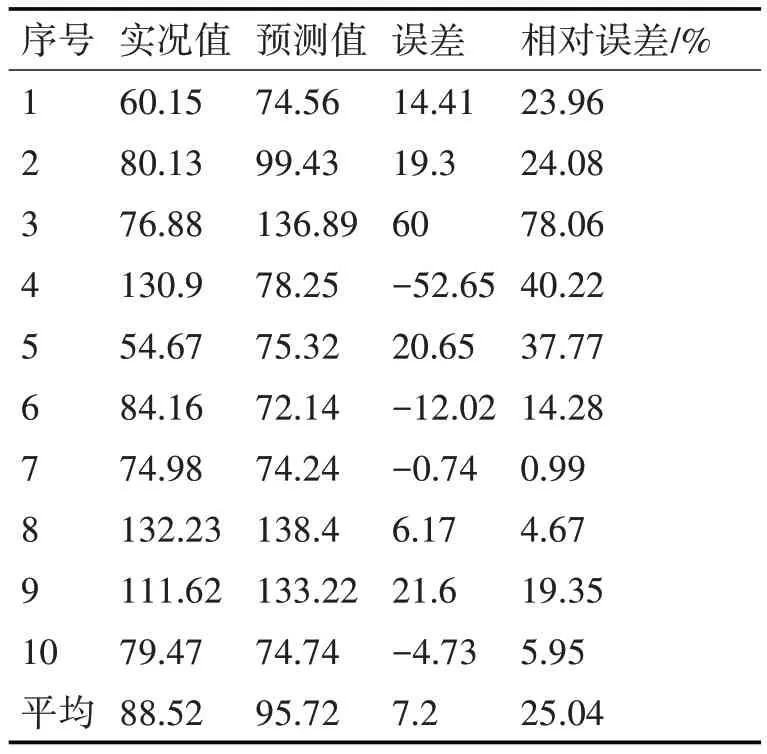
表3 2017年广西冷湿天气冲量项神经网络模型预报结果

3.5 遗传神经网络模型预报

遗传神经网络模型的初始遗传种群数设为50，进化计算50 代。在遗传运算中控制码交叉概率为0.9，阈值和权系数交叉概率为0.6，变异算子的变异概率均设为0.05。神经网络输入节点为6，输入节点为各方程的预报因子数，隐节点个数的搜索空间设定为输入节点的0.5 倍~1.5 倍，网络连接权的初步解空间为（-2，2）。网络训练200 次，学习因子设为0.5，动量因子为0.75。遗传神经网络建模样本数为114，预报模型拟合误差为17.48。表4给出了遗传神经网络模型10 个独立预报样本的预报结果，从表中可见，10 个独立预报样本实际预报平均值为81.93，实况平均值为88.52，误差平均为-6.59，预报值总体小于实况平均值，平均相对误差为22.99%，较逐步回归方法减小了3.95%。

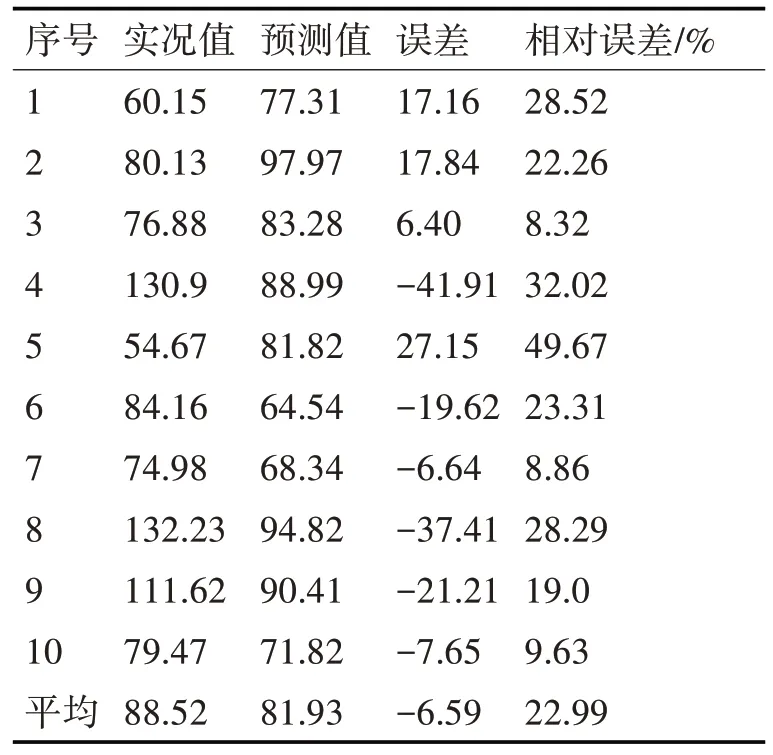
表4 2017年广西冷湿天气遗传神经网络模型预报结果

4 结语

本文提出三种基于机器学习算法的冷湿天气预报模型，并在天气预报中进行应用试验，支持向量回归模型预报效果最好，平均相对误差仅为22.58%，其次为遗传神经网络模型和冲量项神经网络模型，平均相对误差分别为22.99%、25.04%。基于机器学习算法的预报准确率高于传统的逐步回归方法，三种机器学习算法平均相对误差较逐步回归方法减小了3.4%。