电场强度对凸柱面静电空气喷涂特性及成膜影响

张淑珍,杨 凯,李金霞,魏兴佳

(兰州理工大学机械工程学院,甘肃 兰州 730050)

目前对被喷涂面为平面的喷涂过程及涂膜分布的研究较为成熟[1],而曲面因其种类较多、形面曲率变化较大等因素,其喷涂过程及膜厚分布规律仍是研究热点和研究难点[2]。静电空气喷涂成膜研究属于复杂的气液两相流问题[3],数值模拟处理两相流的措施有Euler-Euler法[4-5]及Euler-Lagrange法[6-7],前者将空气相和涂料液相都处理为连续相,不能计算涂料雾滴的运动速度和路径;后者则以气相为连续相,以涂料液滴为离散相,利用牛顿第二定律可推导出涂料液滴的运动规律。故诸多研究人员,如Ye、Osman等[8-9]都采用Euler-Lagrange法研究静电喷涂成膜特性。在实际喷涂作业过程中会遇到各种各样的加工形面,其中凸柱面是常见的产品表面曲面之一。本文以凸柱面静电空气喷涂成膜特性为探究对象,研究电场强度对凸柱面成膜高度分布的影响规律,以便为优化喷涂作业轨迹和研发静电空气喷涂设备提供参考。

1 静电空气喷涂输运过程模型

1.1 连续相模型

欧拉-拉格朗日(Euler-Lagrange)模型中,将气体处理为连续相,且气体流动满足如下方程。

质量守恒方程为:

(1)

动量守恒方程为:

(2)

其中:

式中:ρ为流体密度,t为时间,V为气体速度,▽和▽P为引入的算子,F为外力,μ为黏度,P为表面应力,x、y、z为直角坐标,i、j、k分别为X轴、Y轴、Z轴方向的单位向量。

雾化涂料粒子在成形空气作用下,流动处于湍流状态,还需要建立相应的湍流模型(realizableκ-ε模型)来封闭动量方程。其中,κ表示湍动能,ε表示耗散率[10]。

1.2 离散相模型

本文采用离散相模型来求解雾化涂料微粒的运动轨迹。跟踪颗粒运动轨迹模型主要包括颗粒力的平衡和颗粒力矩平衡。

1.2.1颗粒力的平衡方程

Fluent通过对离散相粒子(涂料雾化液滴)上的力平衡积分来预测其运动轨迹,该力平衡方程为:

(3)

式中:mP和uP分别为涂料雾滴的质量和速度,u为气相速度,τ为雾滴的弛豫时间,ρP、ρ分别为涂料雾滴密度、气相(气体)密度,FP为雾滴所受附加力。

1.2.2颗粒力矩平衡方程

考虑粒子的旋转,需求解关于角动量的常微分方程:

(4)

式中:IP为颗粒的转动惯量,ωP为颗粒的角速度,ρf为空气密度,dP为颗粒直径,Ω为相对颗粒-流体角速度,Cω为颗粒转动阻力系数,T为作用在颗粒上的力矩。

1.3 喷涂静电场

由于电磁场与流体之间存在耦合作用,因此本文采取磁流体动力学方法对荷电液滴在喷涂过程中所受静电场作用进行分析。通过麦克斯韦方程描述电磁场:

(5)

式中:B为荷电粒子运动产生的磁场强度,E为喷涂电极和被喷面间的电场强度,D为电场感应场强度,H为磁场感应场强度,q、je分别为荷电粒子电荷密度和电流密度向量。

1.4 雾化液滴的输运和沉积过程

涂料颗粒输运过程中,荷电液滴承受的静电场力可分为荷电涂料液滴间的电场力F1(N)和荷液滴与工件形面间的电场力F2(N),其表达式如下所示:

(6)

式中:E1为带电涂料液滴间的电场强度,E2为带电涂料液滴与目标壁面之间的电场强度,Q为液滴带电量。

黏附模型、反弹模型、附壁射流模型、飞溅模型为涂料液滴与被喷靶面常见的4种碰撞模型[11]。液滴Weber数ew通常用来判断碰撞模型,其计算公式如下:

(7)

式中:ρdrop为涂料雾滴密度,udrop为涂料雾滴法向速度,ddrop为涂料雾滴飞向工件形面时的直径,σ为涂料雾滴表面张力。

2 凸柱面喷涂过程数值模拟

2.1 计算域及网格划分

本文研究的喷枪模型原型为美国固瑞克Pro xp静电空气喷枪,图1为喷枪空气帽示意图。模型中静电极针的直径为0.5 mm,可输出不同电压,极针周围为涂料入口,直径为1.5 mm。该模型具体参数按文献[5]设置。

图1 静电空气喷枪空气帽模型

为使数值模拟精确,本文采取多区域网格划分方式对计算域进行切分,喷嘴处网格较密,为四面体网格,其他区域为六面体网格,总计约116万个网格,平均扭曲度为0.171 36,平均正交质量为0.834 86,完全满足计算精度要求。考虑到具有代表性的是凸柱面,故选用最大曲率为0.007 0的凸柱面作为静电空气喷涂研究对象,该模型的计算域为300 mm×300 mm×250 mm的六面体,涂料出口孔与被喷涂凸柱面形面间最短喷涂距离为220 mm。喷涂距离即喷枪涂料出口孔到被喷形面上某点的距离,图2中最短喷涂距离为涂料出口孔到被喷涂凸柱面中心点的距离。

图2 凸柱面喷涂计算域

2.2 参数设置和求解

不同电压下凸柱面的喷涂数值模拟参数设置包括边界条件设置和初始条件设置:连续相中心雾化口、辅助雾化口和扇面控制口设置为质量流量入口;离散相模型计算中,质量流量入口、压力出口和交界面均置为“escape”,被喷涂面置为“wall-film”,其他壁面均设为“reflect”;物理模型开启“Stochastic Collision、Coalescence、Breakup”;被喷涂凸柱面电压置为0 kV,涂料密度为1 200 kg/m3,涂料黏度为0.096 86 kg/(m·s),喷嘴喷涂流量为0.001 32 kg/s,时间步长为0.001 s,喷涂时间为5 s;应用TUI指令激活MHD模型。参数设置完成后使用SIMPLE算法对模型求解计算。

3 数值模拟结果与分析

3.1 凸柱面喷涂域电场分析

对凸柱面喷涂模型进行喷涂过程模拟,其中k表示球形面曲率。将极针输出电压分别设置为5、10、20、40、60、80 kV进行喷涂仿真,得到如图3所示的电势分布云图。

图3 电势分布云图

从整组电势分布云图明显看出,喷枪极针附近电势等势线的散布较为密集,电场强度明显大于其他区域,且极针上场强最大;离喷枪极针距离越大,等势线的空间分布越来越稀疏,电场强度亦随之减小;在喷嘴位置附近,涂料雾滴在较大电场力作用下做定向加速运动,并伴随明显雾化现象;随着场强递减,涂料液滴所受电场力亦逐步变小。

3.2 电场强度对凸柱形面喷雾流场的影响

通过仿真得到不同电压下凸柱面在计算域中心截面处的喷雾流场速度云图,如图4所示。

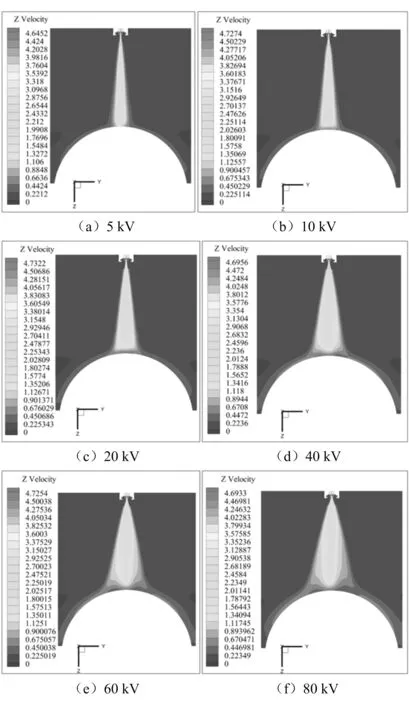
图4 流场速度云图

从该组云图不难发现,云图中心轴附近的空气流速较大,离喷嘴涂料出口越近,空气流速越大,且在喷嘴处气流速度达到最大值;离喷嘴距离变大,气流速度逐渐变小;气流的径向流动几乎全部集中于喷嘴附近和被喷涂面附近;随着极针输出电压变大,空气流场云图在被喷涂形面曲率最大方向延伸越明显,且喷雾流场在计算域所占比例越大,即高电压使涂料液滴雾化更充分,使雾化涂料液滴受到更大的电场力,在计算域中飞行速度更大,空气流域在整个计算域所占比例更大。

3.3 电场强度对涂料液滴分布的影响

分别设置极针电压为5、10、20、40、60、80 kV进行仿真,图5为不同电压下凸柱面喷涂计算域中喷雾流场中的涂料液滴粒径分布图。从该组图不难发现,喷嘴处涂料颗粒分布较密,且涂料粒径较小,雾锥面上及凸柱面主要成膜区的粒径较大,散布在主要成膜区域外的形面上涂料粒径较小,涂料小液滴合并不明显;随着极针输出电压增大,涂料雾粒散布空间越大,涂料液滴的破碎更加明显,涂料雾滴合并减弱。

图5 喷雾流场中涂料粒径分布图

3.4 不同电压与凸柱面喷涂成膜分布关系

通过求解凸柱面静电空气喷涂模型中的涂料沉积模型,得到了相同喷涂参数条件下不同电压的凸柱面喷涂成膜云图。图6所示为电压设置为5、10、20、40、60、80 kV时凸柱面上涂膜厚度分布云图。

图6 涂膜厚度分布云图

从图6可以看出,整组云图中凸柱面静电空气喷涂涂膜基本为椭圆状和椭圆环状,极针输出电压为5 kV和10 kV的成膜形面为椭圆状,涂膜在Y轴方向延伸明显;5 kV的成膜图形中心为椭圆形涂料聚集区,椭圆状涂膜向外涂膜厚度逐渐降低为零;10 kV的成膜图形中心为圆环形涂膜聚集带,且在X轴方向上形成两个显著的圆形涂料聚集团,圆环中心区域为厚度均匀的涂膜区,从圆环向外涂膜厚度逐步减小为零;电压为20、40、60、80 kV时为椭圆环状涂膜,被喷涂工件形面中心处未形成涂膜,涂膜厚度从圆环环带中心向外递减,且涂膜环带中形成涂膜小圆团或条形涂料聚集带;电压越大,成膜面积越大,涂膜由椭圆逐渐变为圆环,涂膜环带中形成的条形涂膜聚集带越来越小,最后形成涂膜小圆团;电压为5、10、20、40、60、80 kV时涂膜膜厚最大值分别为1.876 5、1.986 7、1.688 7、1.256 4、0.835 4、0.721 6 mm,涂膜厚度整体变化趋势为逐步变小。

分别提取图6中心处X轴和Y轴方向上的涂膜厚度值,得到了图7所示的涂膜厚度分布曲线图。其中,图7(a)、(b)分别表示凸柱面涂膜X轴与Y轴方向的涂膜厚度分布。

图7 不同电压凸柱面面静电空气喷涂涂层厚度分布

由图7可看出,电压为5 kV的喷涂成膜模型在凸柱面上X轴方向和Y轴方向上的涂层厚度分布都呈现出不同的变化规律,即被喷涂形面中心位置涂膜厚度最大,从中心(X=0和Y=0处)向轴正负两个方向上涂膜厚度都逐渐减小为零,但在Y轴上的涂膜厚度减小趋势相对缓慢;电压为10 kV和20 kV的喷涂成膜模型在X轴方向和Y轴方向上的涂层厚度分布都呈现出相同的变化规律,即被喷涂形面中心位置涂膜厚度较小,从中心(X=0和Y=0处)向轴正负两个方向上涂膜厚度先增大后减小最后变为零,但在Y轴上的涂膜厚度减小趋势相对缓慢;电压为40、60、80 kV时,在成膜面上X轴方向和Y轴方向上的涂层厚度分布都呈现出相同的变化规律,即被喷涂形面中心位置涂膜厚度为零,从中心(X=0和Y=0处)向轴正负两个方向上涂膜厚度先增大后减小最后变为零,且两者在X轴和Y轴上的涂膜厚度曲线的形状也相似,但在Y轴上的涂膜厚度曲线分布宽度大于X轴上的。

4 结论

1) 电场强度变化不影响凸柱面喷涂计算域中的电势分布形态。越靠近极针,等势线分布越密集,电场强度越大。

2) 电场强度变化对凸柱面喷涂计算域中的喷雾流场分布形态有较大影响。随着极针输出电压变大,喷雾流场在计算域的所占比例越来越大,在成膜面附近喷雾流场气相速度越大、喷雾气流的笼罩范围越广;随着与喷嘴距离变大,气流速度逐渐变小。

3) 电场强度变化对凸柱面喷涂计算域中的喷雾流场中涂料粒径分布有较大影响。随着极针输出电压越大,喷雾流场中涂料雾滴在计算域的空间分布越来越大,涂料液滴的破碎明显,涂料雾滴合并减弱;雾锥面上及凸柱面主要成膜区的粒径大于其他位置处的涂料粒径。

4) 电场强度变化对凸柱面静电空气喷涂成膜影响较大。随着极针电压增大,凸柱面成膜由椭圆形涂膜逐渐过渡成椭圆环形涂膜;电压越大成膜面积越大,且中心区域为成膜的空白面积越大,膜厚最大值越小,涂膜从圆面中心向外放射状分布趋势明显。