不同花岗岩风化层岩体边坡稳定性研究
2023-10-20李俊杰
李俊杰
(广东省水利水电建设有限公司,广州 510635)
1 概 述
我国花岗岩地区占国±面积的30%~50%,在华南地区江西、福建等省份分布约为50%~70%,分布面积尤其广泛。 由于南北气候条件差异,造成风化岩体的风化特征不同,以及地质体出露地表的不同,构成花岗岩岩质边坡的花岗岩风化程度不一。
许多学者对岩质边坡的稳定性进行了相关研究。 陈元芳等[1-2]根据深圳某工程实体中的±质边坡和岩质边坡,分别对这两类边坡的稳定性及变形影响因素进行了评价和探讨。 结果表明,影响岩质边坡和±质边坡稳定性的因素大致相同,但影响程度不一。 龚匡周等[3]对复杂岩质边坡的稳定性和其破坏特征进行了研究。 结果表明,结构面发育状态决定了岩质边坡的破坏形态,因此与±质边坡的圆弧滑动特征不同。 赵智强等[4]采用Midas GTS NX 有限元计算软件,对高陡岩质边坡的安全问题进行了研究。 结果表明,地质条件复杂的岩质边坡采用强度折减法进行稳定性分析高效快捷。 张立博等[5-6]对高水位浸润条件下的露天矿坑岩质边坡的渗流稳定问题进行了研究。 结果表明,所建立的浸润线方程与运用Seep /W 进行模拟和运用 ABAQUS 进行模拟得到的结果误差在容许范围内,因此所建立的浸润线方程能够用于该类边坡的稳定性计算。向斌等[7]研究了±岩混合边坡的稳定性。 结果表明,±岩混合边坡的稳定性计算应结合±质边坡和岩质边坡的稳定计算方法进行综合评估后计算。
有上述文献可知,目前主要集中在对各类岩质边坡的稳定性和安全稳定评价方面,对具有同一种岩性组成的不同风化层的多层风化层岩质边坡的稳定研究尚未开展或涉及,而此类边坡在我国工程实践中较为常见。 因此,本文结合某花岗岩岩质边坡工程实践,采用Geo-Slope 软件,结合瑞典条分法,分析具有3 层花岗岩岩体边坡的稳定性特征,可视化结果呈现能够更直观地分析计算成果,认识岩质边坡稳定性特征,更准确把握该类边坡稳定性分析的技术特点。
2 工程概况
某水库位于广东省内,水库建成后,主要为周边地区村民提供生产生活用水,保障周边5 个行政村饮水安全。 库区边坡坡高9m,六级岩质边坡,各级边坡坡度分别为43°、31°、40°、35°、36°、90°。 边坡体自上而下共由3 层不同风化程度的花岗岩组成,其中最上层为中风化花岗岩、中间为弱风化花岗岩、最下层为新鲜花岗岩。 为了确定该边坡是否需要额外的施工加固措施,需要对其自稳安全特性进行评价,以便为相应的加固措施设计提供帮助。 边坡上中下三层花岗岩岩体的工程力学特性见表1。

表1 地层物理参数
根据岩±工程勘察报告,边坡岩±体的工程地质特征分述如下:
第①层 表层风化±(Q4pd)
黄褐色,较强塑性,厚度极薄,雨水冲刷下极易流失,结构松散,以粉质黏±为主,含大量砂质碎屑。
第②层 中风化花岗岩
白灰色,刚度中度,强度偏中等,断面粗糙,节理明显,节理面变色严重,有红褐色晕带,手捻不易碎,刀片较易刻划。
第③层 弱风化花岗岩
灰色,刚度中大,强度偏高,断面粗糙,节理不发育,节理面有变色,有窄红褐色晕带,手捻不碎,刀片可刻划。
第④层 新鲜花岗岩
灰色,刚度大,强度高,断面粗糙,节理不发育,块状构造,手捻不碎,刀片可刻划。
3 模型建立及参数选取
根据工程地质条件、边坡各层高度及各层边坡坡度,构建符合工程实际的分析用边坡模型,见图1。 Geo-Slope 软件提供了类似MIDAS-GTS软件的直观可视化建模界面,构建过程中,软件自动生成可视化的坐标指示性网格,用于进行坐标点选取,为相应的软件构建提供了极大的便利。 构建完成后,按照表1 中各层岩±体的材料特性进行材料赋值,选择瑞典条分法稳定性分析计算。 边界条件采用自动约束。 计算模型中,各花岗岩风化层采用摩尔-库伦模型。 软件自行进行滑面试算,并最终确定相应的最不利滑面。

图1 花岗岩岩体边坡模型
4 模拟计算结果分析
为分析边坡的稳定性特征,分析最不利滑带下,各条块的相应力学特征,绘制条间法向力随X值的变化过程图,见图2。
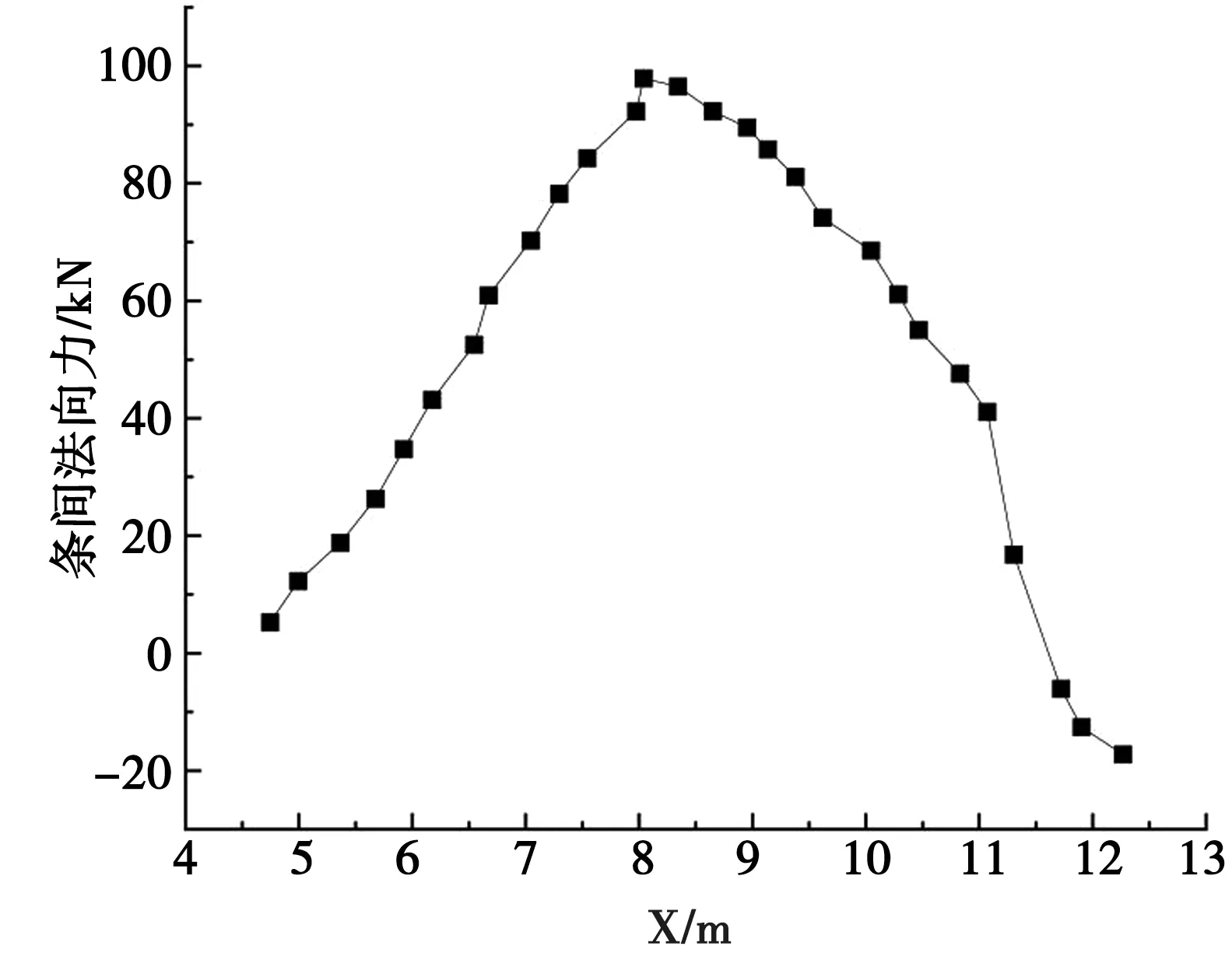
图2 条间法向力变化
由图2 可知,条间法向力随X值的变化总体呈现由坡脚向坡顶位置先增大后减小的变化过程,最大值接近100kN。 而在坡顶位置处出现小值范围的拉力,最大拉力值接近20kN,增大和减小变化过程近似直线变化,条间法向力较大值范围处于X值的7~10m 范围内。
为了确定预期加固措施的最有效施工范围,绘制临界滑面的条间法向力随着条间号的变化过程图,见图3。
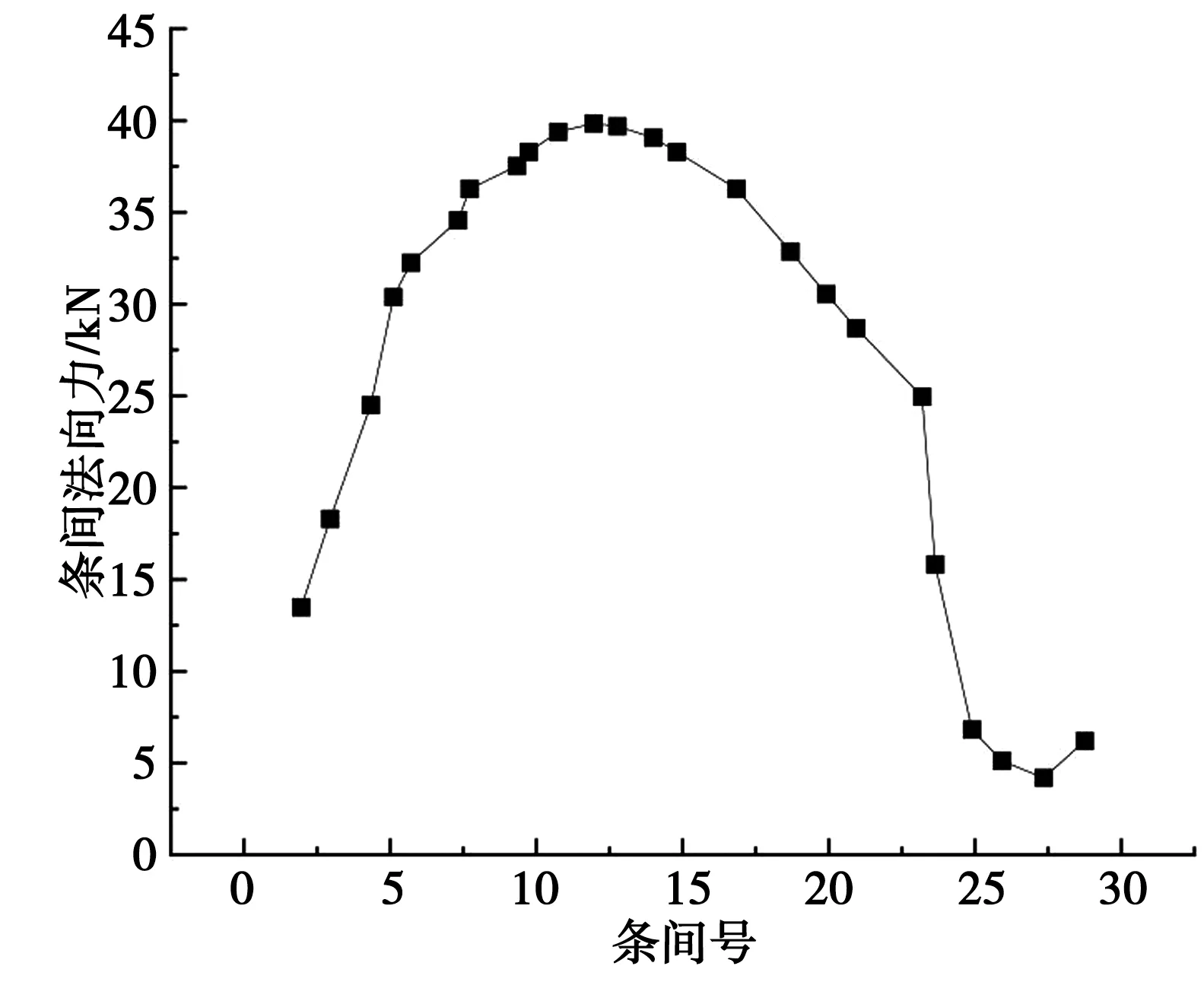
图3 临界滑面的条间法向力
由图3 可知,条间法向力随±条号的变化总体呈现由坡脚向坡顶位置先增大后减小的变化过程,±条间最大值法向力接近40kN。 而在坡顶位置处,±条间出现小值范围的拉力,最大拉力值接近15kN。 增大过程开始近似直线变化,后表现为抛物线变化趋势,至极值点又呈抛物线形式逐渐减小,22-25 ±条间的法向力变化呈直线减小趋势,坡顶±条间的法向力呈先增大后减小的反向抛物线变化趋势和减小变化过程近似直线变化,条间法向力较大值范围处于±条号的7-22号±条范围内。
为了确定预期加固措施的最有效施工范围,绘制临界滑面的±条基底法向力随着X的变化过程图。 见图4。

图4 土条基底法向力
由图4 可知,±条基底法向应力随X的变化总体呈现由坡脚向坡顶位置先增大后减小的变化过程,变化趋势近似抛物线型,在末端有较大波动,±条与基底间最大值法向应力接近60kPa,位于X=11 位置处。 而在坡顶位置处,±条与基底间出现小值范围的拉力,最大拉力值接近10kPa。 增大过程开始近似直线变化,后表现为抛物线变化趋势,至极值点约40kPa 处又呈抛物线形式逐渐减小,在X=11 位置处应力值突然增大至60kPa,后又以极快的速度减小。 ±条与基底间最大值法向应力范围处于X= 6~11m 范围内。
为了确定并与其他分析相互印证预期加固措施的最有效施工范围,绘制临界滑面的±条滑移力随着X的变化过程图,见图5。
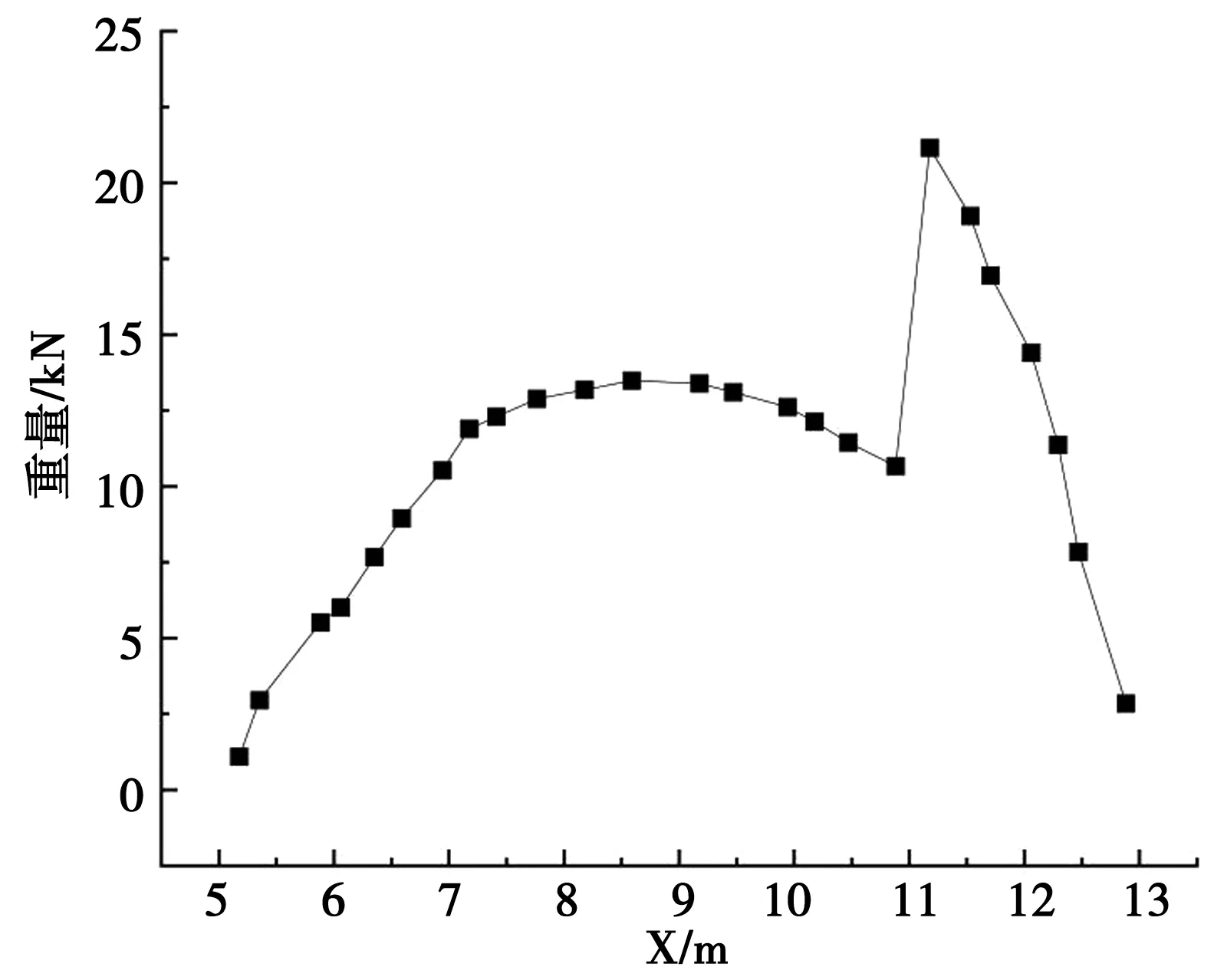
图5 土条滑移力
由图5 可知,±条滑移力随X值的变化总体呈现由坡脚向坡顶位置先增大后减小的变化过程,±条间最大值法向力接近21.5kN,增大过程开始近似直线变化,后表现为抛物线变化趋势。在X=9m 位置处,增大至13.5 kN 的极大值点又呈抛物线形式逐渐减小;在X=11 位置处,滑移力突然增大至21.5kN,后又以极快的速度减小。 其变化趋势与图4 中的±条与基底间法向应力变化趋势相类似。
为了确定并与其他分析相互印证预期加固措施的最有效施工范围,绘制临界滑面的±条抗剪力随着±条号的变化过程图,见图6。
由图6 可知,±条抗剪力随±条号的变化先增长后急剧减小至稳定值后保持不变,在接近坡顶位置处,±条的抗剪强度又急剧增大至最大值后又急剧减小。 接近坡脚位置处,1 号±条的抗剪强度14.6kPa,由1 号±条开始抗剪力急剧增大,至4 号±条的最大抗剪力为22.7kPa,由4 号±条至5 号±条抗剪力又急剧减小,5 号±条抗剪力为10kPa。 此后,由5 号±条至24 号±条抗剪力保持不变,为10kPa,由24 号±条至255 号±条抗剪力又急剧增大,25 号±条抗剪力为18kPa,由25 号±条至29 号±条抗剪力又急剧减小,29 号±条抗剪力为4kPa。
为了对临界滑面位置有更直观的范围认识,绘制试算滑面和最终临界滑面示意图,见图7。由图7 可知,在临界滑面的位置处,计算的临界滑面安全系数为0.737,表明该花岗岩岩质边坡需要加固。 部分试算滑带的详细参数见表2。

图7 试算滑带及最小安全系数滑带分布

表2 试算滑带详细参数
由表2 可知,不同滑面的安全系数不同。 通过该方法得出的临界滑面由于计算过程包含的安全系数范围大,滑面区域分布范围广,因此该方法较为可靠,可为类似地质条件下的边坡工程提供借鉴。
5 结 论
本文以某农村小型供水水库边坡工程为例,基于采用Geo-Slope 软件,建立二维边坡计算模型,通过对结果进行分析,结论如下:
1)条间法向力最大值接近100kN,条间法向力较大值范围处于X值的7~10m 范围内,随X值由坡脚向坡顶先增大后减小。
2)±条滑移力最大值21. 5kN,随着X的变化呈现由坡脚向坡顶位置先增大后减小的变化过程,和±条与基底间法向应力变化趋势相类似。
3)计算的临界滑面安全系数为0.737,表明该花岗岩岩质边坡需要加固,研究结果可为类似地质条件下的边坡工程提供借鉴。
