一种改进的移动机器人轨迹跟踪迭代学习控制*

范雄梅，明 森，姚江燕，杨 婕

（1.中北大学大数据学院，太原 030051；2.中北大学数学学院，太原 030051）

0 引言

迭代学习控制（iterative learning control，ILC）是在1984 年由ARIMOTO S 等提出的一种控制方法，其对重复运动的控制系统轨迹跟踪性能具有改善作用［1］。该控制方法算法简洁，而且可以不依赖于动态系统的精确数学模型，适用于处理不确定、强耦合、非线性、难以建模的复杂系统。因此，迭代学习控制在机器人控制领域的应用被广泛关注。

目前，已经相继出现了P 型、PD 型、PID 型学习律，均可写为

值得指出的是微分系数Γ，比例系数L，积分系数ψ 在PID 算法中的作用各不相同。微分项的作用是使系统的动态特性得到改善；比例项的作用是使系统动作灵敏，速度加快，稳态误差减小；积分项的作用是消除稳态误差，从而提高系统的控制性能。

许多学者利用迭代学习控制算法对移动机器人轨迹跟踪控制进行了研究。文献［2］利用P 型开闭环迭代学习控制算法使移动机器人跟踪期望轨迹。文献［3］引入状态补偿项，并设计新的迭代学习增益矩阵，优化了移动机器人的轨迹跟踪效果。结合PD 型开闭环迭代学习律，文献［4］研究了移动机器人的轨迹跟踪迭代学习控制，仿真结果说明了其收敛速度优于其他算法。文献［5-6］提出了迭代学习控制与智能控制相结合的算法，该算法不依赖于系统的数学模型，为研究非完整移动机器人运动控制问题提供了新方法。更多相关的研究见文献［7-15］。

在迭代学习控制算法中，关于学习增益矩阵的选取目前尚未完善。由于控制算法在无限时间收敛是无意义的，因此，提高迭代学习控制算法的收敛速度值得研究。本文通过对学习律进行改进，在满足迭代学习控制收敛稳定时，收敛速度会明显加快。在PD 型开闭环迭代学习律中添加状态补偿项，并设计新的迭代学习增益矩阵，从而提高跟踪精度。

1 移动机器人运动学模型

轮式移动机器人（wheeled mobile robot，WMR）的运动学方程可描述为

其中，x 和y 是WMR 的坐标位置、θp是WMR 的方位角、vp，wp分别为WMR 的线速度和角速度，表示移动机器人的控制输入。

为了利用迭代学习控制算法对移动机器人进行轨迹跟踪控制，现对式（1）进行离散化处理，即得其离散运动学方程

其中，ΔT 为采样时间。

2 轨迹跟踪问题的描述

引入迭代学习控制算法，选取WMR 的速度作为系统输入up（k）=（vp（k），wp（k））T；WMR 的位姿作为系统输出y（k）=（xp（k），yp（k），θp（k））T；期望位姿状态为q（k）=（xd（k），yd（k），θd（k））T。考虑到实际系统存在噪声和干扰，则移动机器人的运动学模型可表示为

其中，i 为迭代次数；k 为离散时间，且1≤k≤N（k∈N；N 表示自然数集）；N 为采样数；β（k）为状态干扰；γ（k）为输出测量噪声，

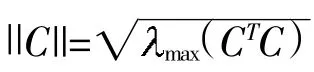
式（3）和式（4）满足如下性质和假设条件。

性质1 考虑理想情形，选取βi（k）=0，γi（k）=0，k∈N，则期望轨迹为

qd（k+1）=qd（k）+B（qd（k），k）ud（k）yd（k）=Cqd（k）

性质2 矩阵B（qi（k），k）为满秩矩阵，有界且满足Lipschitz 条件||B（qi（k），k）||≤bB，||B（q1（k），k）-B（q2（k），k）||≤cB||q1-q2||，其中，k∈N，bB>0，cB>0 为常数。

1）控制输入有界max1≤k≤N||ui（k）||≤bu，其中，N为采样数，bu≥0 为常数。

2）状 态 干 扰 和 输 出 噪 声 有 界：maxi∈N*maxk∈N||βi（k）||≤bβ，maxi∈N*maxk∈N||γi（k）||≤bγ，其中，bβ>0，bγ>0 为常数。

3）每次迭代轨迹从qd（0）的邻域开始：||qd（0）-qi（0）||≤b0，其中，b0>0，i∈N*。

则移动机器人的轨迹跟踪问题即确定up（k）=（vp（k），wp（k））T，使得xp（k）→xd（k），yp（k）→yd（k）和θp（k）→θd（k）。

3 迭代学习控制律的设计

根据控制算法中是否包含当前输出误差信息，迭代学习控制可以分为开环学习和闭环学习，基本结构如下页图1 和图2 所示。

图1 开环学习的基本结构Fig.1 The basic structure of open-loop learning

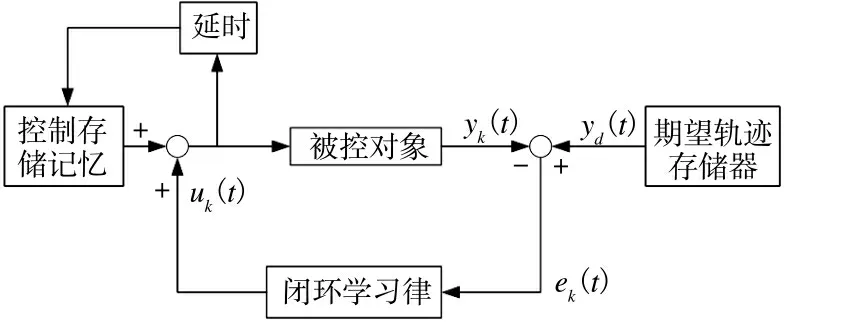
图2 闭环学习的基本结构Fig.2 The basic structure of closed-loop learning

本文采用改进的PD 型开闭环迭代学习控制律，其离散形式为：

其中，ei（k）=yd（k）-yi（k）为系统第i 次运行时的跟踪误差。L1，L2表示有界学习增益矩阵，L3为补偿增益矩阵，满足||L1（k）||≤bL1，||L2（k）||≤bL2，||L3（k）||≤bL3，bL1，bL2，bL3>0。由于［ei+1（k）-ei（k）］与-［yi+1（k）-yi（k）］相等，所以用L3（k）（ei+1（k）-ei（k））来补偿在k 时刻第i+1 次迭代与第i 次迭代之间的迭代误差。添加状态补偿项，不仅提高算法收敛的速度，而且弱化了初始条件和Lipschitz 条件的限制，从而提高跟踪精度。对于移动机器人而言，缩短了其轨迹跟踪时间，同时有效防止外界干扰。

由式（5）的迭代学习控制律，移动机器人轨迹跟踪的控制结构原理如图3 所示。

图3 移动机器人迭代学习控制系统结构Fig.3 Iterative learning control system structure for mobile robot

对式（5）中的学习增益矩阵进行改进，可得

定理1 若式（3）～式（4）满足假设1）～假设3），采用控制律式（6），当迭代次数i→∞时，||ui（k）-ud（k）||，||yi（k）-yd（k）||，||qi（k）-qd（k）||有界并收敛于bβ，bγ，b0（若忽略所有干扰，则ui（k），yi（k），qi（k）分别收敛于ud（k），yd（k），qd（k））的充分条件为||［I+L2（k）B（qi（k），k）］-1［I-L2（k）B（qi（k），k）］||=ρ<1

其必要条件为||［I+L2（0）B（0）］-1［I-L2（0）B（0）］||<1。

详细证明见文献［7］。

4 仿真实验

本文利用Matlab 工具对移动机器人运动学模型进行仿真，若不考虑干扰和噪声，给出P 型开闭环迭代学习控制算法对不同轨迹曲线的跟踪效果。

1）圆轨迹跟踪：参考轨迹xd（t）=cosπt，yd（t）=sinπt，θd（t）=πt+π/2，初始状态xd（0）=1，yd（0）=0，θd（0）=π/2。如图4 ～图6 所示。

图4 圆轨迹随迭代次数的跟踪过程Fig.4 The tracking process of circular trajectory with times of iterations

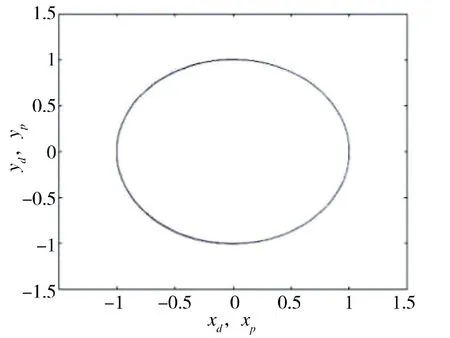
图5 圆轨迹迭代180 次的结果Fig.5 The result for 180 iterations of circular trajectory

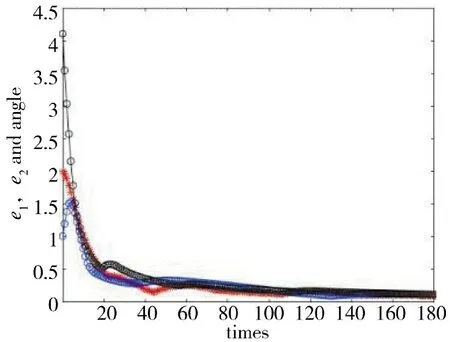
图6 圆轨迹误差迭代收敛过程Fig.6 Iterative convergence process of circular trajectory errors

2）正弦曲线轨迹跟踪：参考轨迹xd（t）=t，yd（t）=sint，θd（t）=tan-1（cost），初始状态xd（0）=0，yd（0）=0，θd（0）=π/4。如下页图7～图9 所示。

图7 正弦轨迹随迭代次数的跟踪过程Fig.7 The tracking process of sinusoidal trajectory with times of iterations

图8 正弦轨迹迭代180 次的结果Fig.8 The result for 180 iterations of sinusoidal trajectory

图9 正弦轨迹误差迭代收敛过程Fig.9 Iterative convergence process of sinusoidal trajectory error

3）指数轨迹跟踪：参考轨迹xd（t）=t，yd（t）=et，θd（t）=tan-1（et），初始状态xd（0）=0，yd（0）=1，θd（0）=π/4。如图10～图12 所示。

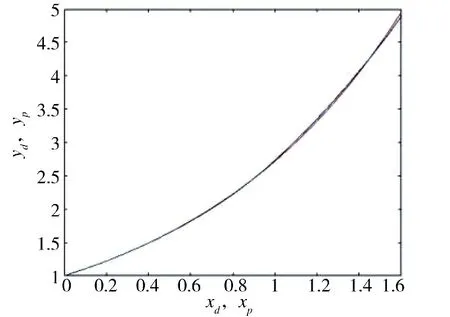
图11 指数轨迹迭代180 次的结果Fig.11 The result for 180 iterations of exponential trajectory

图12 指数轨迹误差迭代收敛过程Fig.12 Iterative convergence process of exponential trajectory error

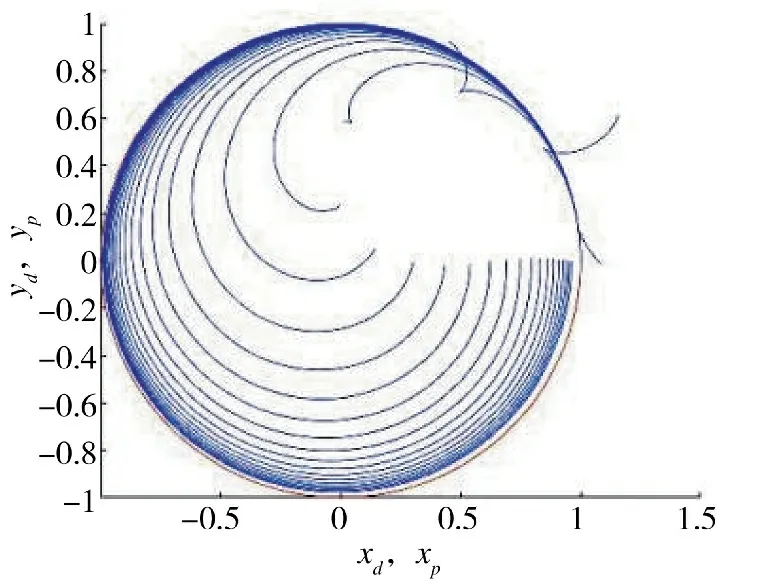
图13 圆轨迹随迭代次数的跟踪过程Fig.13 The tracking process of circular trajectory with times of iterations

图14 圆轨迹迭代20 次的结果Fig.14 The result for 20 iterations of circular trajectory

由图4～图12 可知，不同参考轨迹的跟踪效果也不同。指数轨迹跟踪迭代过程比正弦轨迹迭代过程和圆轨迹迭代过程快，正弦轨迹跟踪迭代过程比圆轨迹迭代过程稍快。仿真结果表明，轨迹越简单，收敛过程越快。

下文给出改进前和改进后的PD 型开闭环迭代学习控制算法对正弦轨迹跟踪效果的影响。

改进前，采用文献［4］中的PD 型学习控制律

由图18 可知，改进后的迭代学习控制算法在迭代次数为10 次时完全收敛，跟踪误差在10 次之后趋于0，在迭代20 次时，基本保持稳定。而改进前的迭代学习控制算法在迭代20 次时才完全收敛，如图15 所示。通过比较可知，改进后的迭代学习控制算法优于改进前的迭代学习控制算法。

图15 圆轨迹误差迭代收敛过程Fig.15 Iterative convergence process of circular trajectory errors

图16 圆轨迹随迭代次数的跟踪过程Fig.16 The tracking process of circular trajectory with times of iterations

图17 圆轨迹迭代20 次的结果Fig.17 The result for 20 iterations of circular trajectory

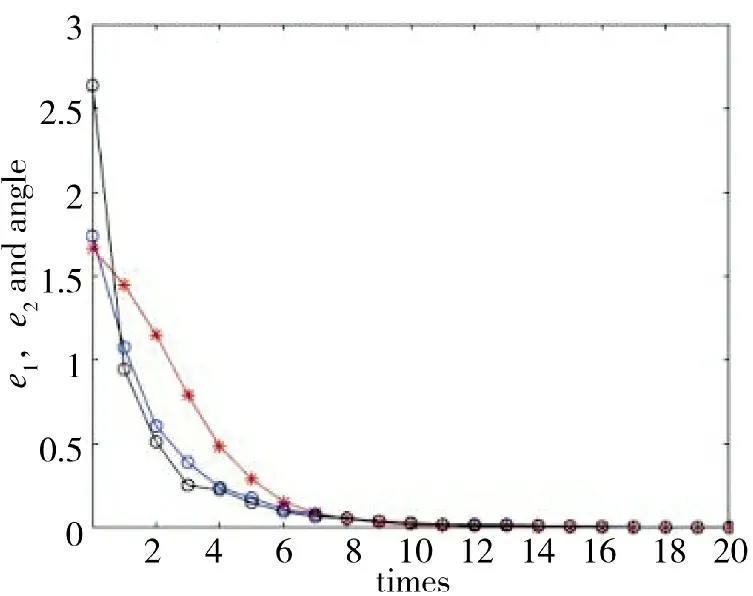
图18 圆轨迹误差迭代收敛过程Fig.18 Iterative convergence process of circular trajectory errors

5 结论

本文运用迭代学习控制算法对轮式移动机器人的轨迹跟踪问题进行了研究。在不考虑干扰和噪声的情况下，对已有的PD 型开闭环迭代学习控制算法进行改进，从而提出一种具有状态补偿项的PD型开闭环迭代学习控制算法。通过改进前后的比较，可知改进后的迭代学习过程更快收敛于期望值且误差更小。表明本文提出的迭代学习控制算法对移动机器人的轨迹跟踪控制具有良好的控制效果。