基于DEM-MBD的高压辊磨机仿真模型及应用研究

任云鹏 李安帅 李旭东 宋 芳

(1.沈阳建筑大学机械工程学院,辽宁 沈阳 110168;2.山东黄金矿业(莱州)有限公司三山岛金矿,山东 莱州 261442)

高压辊磨机是一种新型破磨粉碎设备,具有处理能力强、单位破碎能耗低、设备工作效率高等特征[1]。该设备最先应用于水泥领域,随着技术的不断发展,已经广泛应用于金属矿山领域[2-3]。高压辊磨机的相关研究涉及机械运动学、动力学、离散元等诸多方面,当前研发设计中仍存在现有模型不准确、破碎过程中重要参数无法定量表示等问题。

虚拟仿真技术是改进粉碎设备设计和操作的一项重要方法,它能够比较不同参数设置而不需要物理原型或生产损失的相关成本,其仿真结果的可用性取决于模型的保真度。BILGILI 等[4]用严格的数学模型研究了多个接触颗粒的粉碎,得出了粉碎过程矩阵,但无法考虑到设备参数、颗粒材料性质对粉碎效果的影响。TORRES 等[5]以矿石性质、高压辊磨机工作参数、粉碎工艺为基础,研究了一系列高压辊磨机粉碎的数学模型,包括处理能力模型、能耗模型,但在预测准确度上有所不足,无法应用到工业领域。DANIEL 等[6]通过大量实验开展了关于高压辊磨机数学模型及应用的专项研究,验证和扩展了高压辊磨机的产品粒度分布、处理量以及能量利用率的数学模型。KUMAR[7]使用EDEM 模拟了实验室规格的高压辊磨机,研究了颗粒破碎过程,以及工艺参数和操作参数对处理量和能耗的影响。祖大磊等[8]和何剑伟等[9]根据高压辊磨机破碎过程中的工艺参数、矿石单轴抗压强度、给料粒度及粉碎产品粒度分布对比能耗的影响,提出了利用高压辊磨机比能耗进行计算评估的DUCS 数学模型。鲍诺[10]利用EDEM 软件研究了高压辊磨机工作过程中颗粒运动状态与工作参数之间的关系,得到了不同辊速和粒径下颗粒所受压力随时间变化的规律。张乐[11]利用EDEM 软件模拟了高压辊磨机破碎矿石过程,通过正交试验方法和单因素试验方法研究压辊转速、压辊间隙以及压辊与矿石间的静摩擦因数对矿石破碎效果的影响,但单一的DEM 仿真模型忽视了设备的动态响应,无法真实模拟实际工作状态。在高压辊磨机中,压辊间隙不是一个直接控制的变量,是所施加的压力和颗粒床之间相互作用的结果。以上基于理论的数学模型和基于离散元法的仿真模型由于忽略了颗粒对高压辊磨机运行的影响,无法描述辊隙的动态变化对仿真结果的影响,导致在预测处理量、单位能耗和破碎比时均存在较大误差。

针对高压辊磨机现有模型存在误差和无法描述设备的动态辊隙随颗粒载荷变化规律的问题,为了减小误差,降低企业研发设计成本,在离散元法基础上,提出采用离散元(DEM)和多体动力学(MBD)联合仿真技术对高压辊磨机进行仿真分析,通过对比数学模型、单一离散元仿真模型以及实际工作数据,证实联合仿真模型有着较为理想的结果。

1 高压辊磨机数学模型

1.1 动态辊隙模型

动态辊隙模型是在动辊动力学模型基础上推导而来的,高压辊磨机主要由两个压辊和液压系统组成,液压系统部分蓄能器中的压缩氮气充当液压系统的弹簧。在破碎过程中,动辊和定辊的旋转速度是恒定的,但动辊会因受到物料的挤压力和液压系统提供的力往复平移。动辊的横向移动可以由弹簧阻尼系统来描述,如图1所示。

图1 高压辊磨机动态辊隙模型Fig.1 Dynamic roll gap model of high-pressure grinding rolls

高压辊磨机的辊隙动态变化可由下式表示:

1.2 处理量模型

高压辊磨机的处理量数学模型可以基于设备的设计参数和物料的物理性质进行推导。最常见的处理量数学模型是基于高压辊磨机的辊隙宽度、压辊直径、压辊旋转速度、压辊面长度、料饼密度等参数来进行建模的。图2 是高压辊磨机的粉碎示意图。

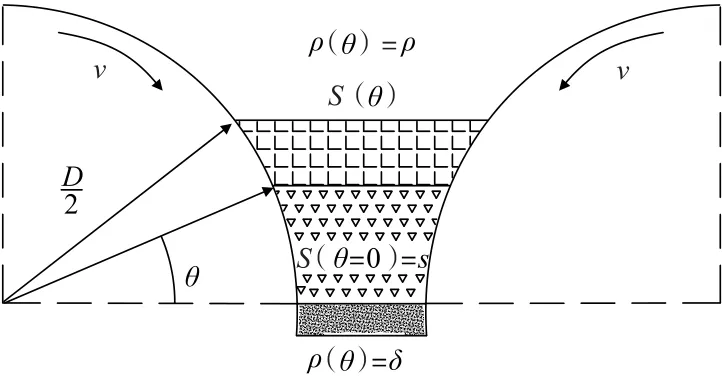
图2 高压辊磨机粉碎示意Fig.2 High-pressure grinding rolls crushing diagram

根据质量守恒定律,物料在挤压区域内,质量不发生改变,并且假设辊面与物料之间不存在相对滑动,则高压辊磨机的单位处理量G可以表示为:

式中,G(θ)为任意圆心角θ下高压辊磨机的单位处理量,t/s;ρ(θ)为任意圆心角θ下物料密度,t/m3;S(θ)为任意圆心角θ下的压辊间隙,m;L为辊宽,m;v为压辊线速度,m/s。

在实际应用中,高压辊磨机的处理量一般指出料口位置处,即θ=0 时,高压辊磨机的理论处理量G为[12]:

式中,δ为料饼密度,一般为物料密度的0.85[13],t/m3;s为出料口间隙,m。

1.3 单位能耗模型

图3 是高压辊磨机压辊受力示意图。

图3 高压辊磨机压辊受力示意Fig.3 Force diagram of pressure roller of high-pressure grinding rolls

如图所示,阴影区域是工作压力的影响区域,在该区域内压辊对物料的挤压力F可以通过压辊的工作压力求得。由于高压辊磨机的工作特点,物料只在压缩区受到压辊的挤压力,故相应的受力区域为压辊的上半部分,因而压辊的挤压力F为:

式中,F为压辊对物料的挤压力,kN;P为压辊的工作压力,MPa;D为辊径,m。

则垂直方向上的挤压力F引起的转矩T为:

式中,T为转矩,kN;β为发生层压粉碎角度的一半。

高压辊磨机具有2 个压辊,那么总功率是压辊垂直方向上挤压力F和压辊线速度v乘积的2 倍,故功率P为:

单位能耗为总功率P与处理量G的比值,故高压辊磨机的理论单位能耗W为[14]:

式中,W为理论单位能耗,kW·h/t;G为处理量,t/h。

1.4 破碎比模型

平均破碎比是破碎机的一个重要性能参数,用来衡量高压辊磨机对物料的破碎效果。平均破碎比i通常定义为物料经过高压辊磨机破碎后,进料的平均粒径与出料的平均粒径之比,该种方法求得的破碎比能较为真实地反映破碎程度。将颗粒划分为体积或质量相等的两部分的粒径d50亦被称为中位径或中值粒径,常用来表征颗粒样品的平均粒径[15]。高压辊磨机出料的平均粒径可以用d50表示,d50可通过产品粒径分布函数罗逊—拉姆勒(Rosin-Rammler)求得。该函数是一种经验公式,可以用来描述颗粒大小的分布情况。该函数的形式如下[16]:

式中,ϕ(d)为累计粒度产率分布函数;d为颗粒粒径,mm;c,n,dmax是根据经验数据确定的参数,其中dmax为破碎产品中最大粒径,mm。

则高压辊磨机的理论平均破碎比i为:

式中,D50和d50分别表示破碎前后累计粒度分布百分数达到50%时所对应的粒径。

2 DEM-MBD 联合仿真模型建立

考虑到高压辊磨机是一个复杂的多体动力学系统,其运行状态会受到多个因素的影响,当物料与压辊之间的挤压作用力导致物料材料性质发生变化时,如粉碎过程中的物料磨损和破碎,则必须考虑设备的动态响应,如辊隙的动态变化,因为它会影响使用DEM 进行模拟仿真的效果。对于单一DEM 仿真模型,只能考虑压辊固定间隙,无法反映辊隙的动态变化对系统的影响。而辊隙的变化又是影响高压辊磨机处理量、单位能耗、破碎比的关键因素,所以现有的DEM 仿真模型在预测高压辊磨机的性能上具有较大误差。高压辊磨机的MBD 仿真需要对压辊施加瞬态载荷,以便描述辊隙随载荷变化而变化的特性。DEM-MBD 联合仿真利用两软件之间的数据交互功能,将物料破碎过程中引起的设备实时动态响应又反馈给破碎过程。DEM-MBD 联合仿真模型引入了辊隙的动态变化,可以更真实、更准确地模拟高压辊磨机的运行状态和性能,从而提高仿真结果的可靠性和有效性,故本文提出采用DEM-MBD 联合仿真方法预测高压辊磨机性能指标。

2.1 联合仿真方法

高压辊磨机联合仿真的流程图见图4。当仿真开始后,MBD 部分将定义完材料参数和运动参数的动力学模型传递给DEM 部分,DEM 部分颗粒工厂产生颗粒,然后由EDEM 软件计算确定每个颗粒的位置和速度,以及颗粒之间和颗粒与几何体之间的作用力。DEM 部分结束后,EDEM 将几何体上的等效粒子力和力矩再反馈给MBD 部分,MBD 部分由Motionview 软件实现求解MBD 的控制方程,并计算几何体的位置和速度。

图4 DEM-MBD 联合仿真流程图Fig.4 DEM-MBD co-simulation flow chart

2.2 多体动力学模型

高压辊磨机几何机构的精确构建是联合仿真的关键,以KHD375ϕ1400-1000 型高压辊磨机为研究对象,利用SolidWorks 软件构建几何机构模型,包括定辊、动辊、机架、液压缸、氮气蓄能器、喂料装置六大部分,如图5所示。

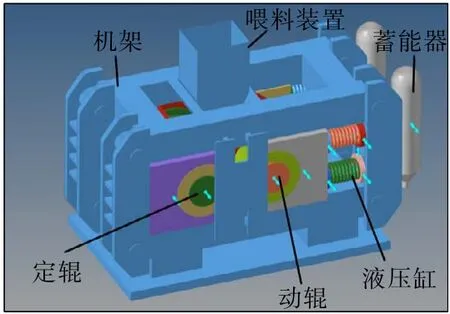
图5 高压辊磨机几何模型Fig.5 Geometry model of high-pressure grinding rolls

2.2.1 约束关系构建

将构建好的KHD375ϕ1400-1000 型高压辊磨机几何模型导入Motionview,此时模型之间只存在空间位置关系而不存在运动学上的约束关系。因此为保证虚拟高压辊磨机的准确运动,首先应根据各零部件的实际运动关系构建模型之间的约束关系。其约束关系如表1所示。

表1 约束关系Table 1 Binding relationships

高压辊磨机零部件的几何关系和约束关系构建完后,需要进一步施加作用在压辊上的旋转运动,从而使高压辊磨机能够实现破碎作业。

2.2.2 液压系统参数理论计算

高压辊磨机中的液压系统由3 个主要部件组成:液压缸、氮气蓄能器和液压油。蓄能器中的压缩氮气充当液压系统的弹簧,其刚度可通过初始氮气压力进行调整,初始油压和氮气压力的组合有效地决定了弹簧的非线性刚度响应。图6 为液压系统力学模型图,当力从f1增加到f2时,它会引起压辊位移Δs,该位移被传递到横截面积为ap的活塞上,使氮气蓄能器中的压力从p1增加到p2。

图6 高压辊磨机液压系统力学模型Fig.6 Mechanical model of hydraulic system of high-pressure grinding rolls

液压系统部件参数与弹簧刚度k和阻尼系数c有关,可通过以下公式估算[17]:

式中,n是多变指数;p0是初始氮气压力,MPa;V0是初始氮气体积,m3;p1是初始液压,MPa;ap是液压缸的横截面积,m2;np是气缸数,个;g 是重力加速度,m/s2。该模型考虑了液压系统的主要部件,但未考虑其他部件,如阀门、油管、油黏度等。

根据实际高压辊磨机运行参数,依据上述公式计算出液压系统的弹簧刚度k和阻尼系数c,通过在Motionview 中添加弹簧系统部件并设置弹簧刚度k和阻尼系数c,实现液压系统的代替。

2.3 离散元模型

2.3.1 颗粒破碎模型的选用

目前EDEM 中有2 种用于模拟颗粒破碎的模型:Bonding 键模型和Tavares 破碎能模型。Bonding键模型是将小颗粒通过Bonding 键粘结成大颗粒,以键的断裂来模拟颗粒的破碎。Bonding 键模型在颗粒形状和大小相对均匀的情况下表现较好,但在颗粒形状和大小差异较大时,可能会出现较大误差,并且计算量比较大,破碎后无法对颗粒粒径进行统计。Tavares 破碎能模型是一种基于经验的破碎模型,当冲击能大于破碎能时,颗粒发生破碎,没有破碎的颗粒也会受到损伤,产生更小的破碎能。该模型基于经典的Kick、Rittinger 和Bond 破碎理论,考虑了影响颗粒内部的应力分布和破碎的各种因素,如颗粒的强度、形状、大小、载荷等[18]。Tavares 破碎模型适用于各种形状和大小的颗粒,且在颗粒破碎前后的形状不会发生太大变化的情况下表现较好,并且计算速度快,可对破碎后颗粒进行粒径分布、获取破碎比等后处理,能直观展示破碎效果。

高压辊磨机仿真破碎过程颗粒数量巨大,且需要分析颗粒破碎后的破碎比、处理量和单位能耗等。相比Bonding 键破碎模型,Tavares 破碎模型能够方便对颗粒粒径进行统计,并且能同时满足其他的仿真需求。Tavares 破碎模型原理如图7所示。

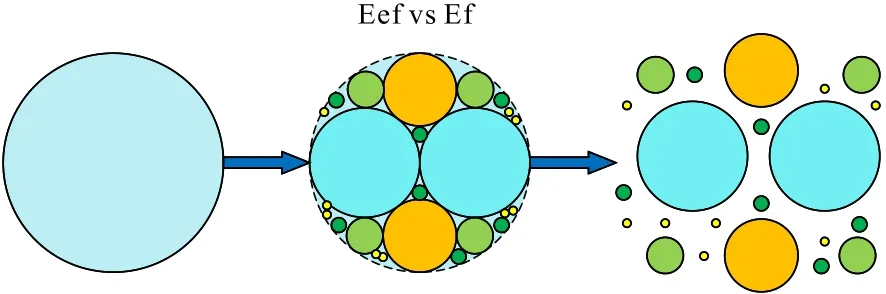
图7 Tavares 破碎原理Fig.7 Tavares crushing principle

在Tavares 破碎模型中,每个颗粒都有特定的破碎能量,根据其大小、平均值和标准偏差进行分配。这个能量根据公式[19-20]所描述的分布而变化。

式中,E为破碎能量分布,J/kg;Emax为能量分布的上限值,J/kg;E50为能量分布的中值,J/kg;σE为标准差。

破碎能量的中值由以下公式给出:

式中,E∞为极限破碎能,J/kg;φ是根据试验数据调整的参数;KP和Kst分别为颗粒和钢的硬度,GPa;dp为颗粒的大小,mm;d0为矿石中特征颗粒的大小,mm。

当颗粒受到挤压而未发生破碎时,它将受到损伤,之后颗粒会产生新的破碎能E′f,新的破碎能会低于其原破碎能Ef:

式中,Ef为颗粒的破碎能,J;eEk为有效碰撞能量,J;D为损伤系数;γ为损伤累积系数。

Tavares 破碎模型主要是基于参数t10,t10表示产品中小于母粒径1/10 的碎片比例,由公式描述为:

式中,A和b是根据试验数据调整的参数。t10值越大,新产生的颗粒就越细。

根据Tavares 团队研究成果,参考RODRIGUEZ等[21]校核的Tavares 破碎模型参数来定义物料的破碎参数,具体破碎参数如表2所示。

表2 Tavares 破碎模型参数Table 2 Tavares crushing model parameters

2.3.2 仿真时间步长理论计算

在EDEM 仿真中首先需要合理地设定时间步长,时间步长的设定需要考虑多个因素,如模拟的物理现象、计算机的性能、仿真时间等等。时间步长的大小对于仿真结果的准确性和计算速度都有很大的影响,如果设置时间步长过大,则会令仿真结果不收敛,并且对于硬球颗粒,过大的时间步长可能会使某些颗粒穿过设备,使得仿真结果不准确。如果设置的时间步长太小,则会要求计算机较高的配置并且耗费时间较长。因此,针对不同的仿真工况需要选取适当的时间步长。

颗粒在发生碰撞时,百分之七十的能量是通过瑞利波消耗的,因此临界的仿真时间步长需要根据瑞利波的传播速度决定。瑞利波是指当两个单元发生碰撞时,因单元表面受到变应力而产生的沿单元表面传播的偏振波。瑞利波传播时,单元表面的能量最强,并且沿着球心方向上显著减弱。各向同性材料中,瑞利波呈指数形式衰减;各向异性材料中,则随着深度呈振荡衰减,振荡幅度的包络线呈指数形式。通常情况下,如果传播深度超过两倍波长时,振幅就已非常小[22]。

弹性固体颗粒表层的瑞利波速度计算公式为:

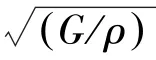
式中,ν是颗粒的泊松比,则由上式求出β1的近似解为:

瑞利波速度进一步写成:

由于两接触颗粒的接触作用力仅限于发生在碰撞的两颗粒上,而不应该通过瑞利波传递到其他颗粒上,因此时间步长必须小于瑞利波传递半球面的时间,故可求得时间步长的理论计算公式为:

当由不同粒径的颗粒组成的系统时,时间步长应为:

上述公式是在两颗粒为静态或者相对运动速度较小的情况下得出的结论,由于高压辊磨机的颗粒运行并不剧烈,故通过上式取得步长可使仿真模型稳定。但是考虑到高压辊磨机仿真破碎颗粒数量巨大,为使计算稳定可取上式的1%～10%。

2.4 仿真参数设定

三山岛金矿KHD375ϕ1400-1000 高压辊磨机设备参数和操作参数如表3所示。

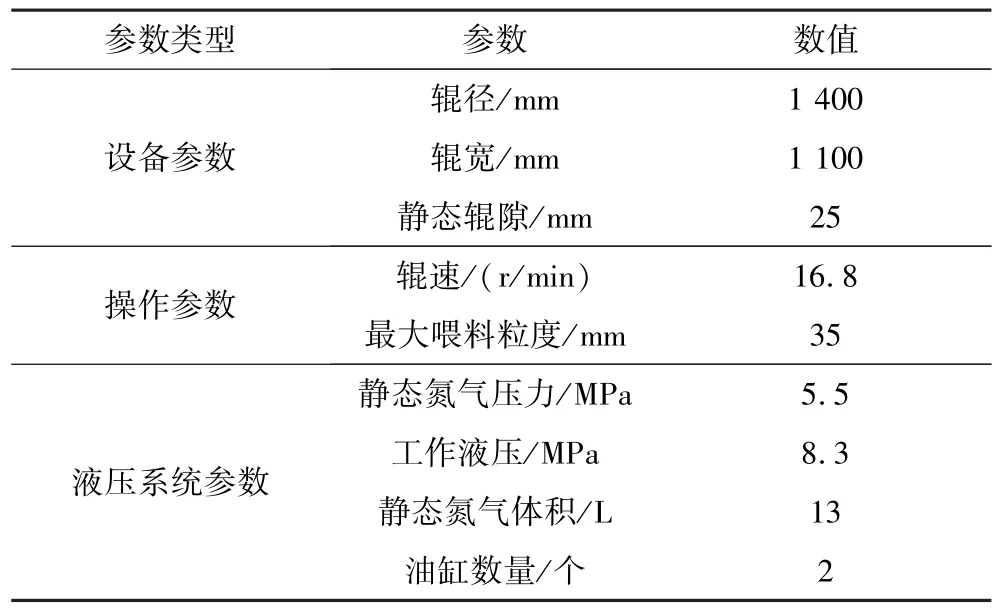
表3 高压辊磨机设备参数和操作参数Table 3 Equipment parameters and operating parameters of high-pressure grinding rolls

表4 为该仿真中使用的材料参数和接触参数,这些参数参考了BARRIOS 等[23]和RODRIGUEZ 等[21]的研究,并根据EDEM 软件中材料数据库(通用材料模型数据库-GEMM)的安息角结果进行验证。

表4 离散元仿真参数Table 4 Discrete element simulation parameters

3 联合仿真模型验证与分析

为了验证DEM 和MBD 联合仿真在高压辊磨机预测处理量、破碎比和单位能耗上的准确性,以及证明该联合仿真方法的优势,以三山岛金矿KHD375ϕ1400-1000 型高压辊磨机实际工作数据作为对比目标,对辊隙的动态特性进行验证与分析,以及对前文所述的数学模型、单一离散元仿真模型和联合仿真模型进行对比分析。试验设备、控制系统和整体仿真模型如图8所示,在EDEM 软件中出料口位置设置GeometryBin(几何选择区域)和Mass Flow sensor(质量流传感器),用于监测破碎出料颗粒粒径大小和排料流量。

高压辊磨机进料的一个重要的特性是,需要一定高度的料柱给位于压辊之间的颗粒床施加压力[24]。为了避免进料的堵塞,根据CLEARY 等[25]的相关结论,通过DEM 模拟证明,料斗中的物料高度至少应等于其宽度,超过这个高度,物料额外的压力就会逐步传递到料斗壁上,而不影响高压辊磨机的性能。因此,仿真中采用的喂料高度为压辊的宽度,只有当DEM 颗粒达到此高度时,仿真的结果才视为有效结果。并且在仿真过程中,保持相同的颗粒产生速度,以保持破碎过程的稳定。

3.1 辊隙的动态变化

通过在Motionview 中添加动辊和定辊之间的位移输出,从而得到辊隙在破碎过程中的动态变化,仿真结果具体如图9所示。

图9 高压辊磨机辊隙变化Fig.9 Roll gap change of high-pressure grinding rolls

从图9 可以看出,物料在0.5 s 时接触压辊,1.5 s 后喂料高度到达理论要求,在稳定后辊隙保持在35.5 mm 左右。根据矿山提供的数据,破碎过程中KHD375ϕ1400-1000 型高压辊磨机的辊隙在30～40 mm之间,该仿真结果符合工程实际。通过DEMMBD 联合仿真可以模拟高压辊磨机辊隙的动态响应,研究不同工艺参数下辊隙的变化规律,能够帮助设计人员更好地了解系统的性能和特性,优化设计方案。

3.2 处理量

通过EDEM 导出的质量流量数据和根据理论计算数据以及高压辊磨机工作数据,绘制各模型预测处理量,结果如图10所示。

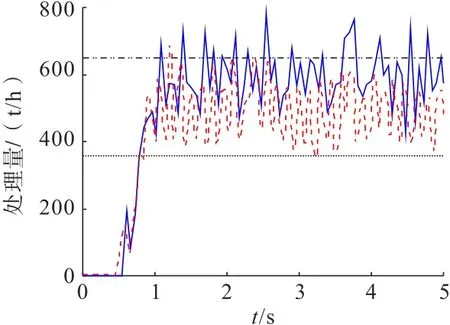
图10 各模型处理量结果曲线Fig.10 Results curve of treatment volume of each model

比较了DEM-MBD 联合仿真、DEM 仿真以及处理量数学模型各自的预测值与矿山实际处理量数据。由图10 可以明显看出,通过数学模型预测的处理量数据和实际工作数据偏差较大,可能是数学模型无法考虑到工作压力、辊隙变化、喂料粒径大小、物料物理性质等其他参数对设备的影响。DEM-MBD 仿真结果与DEM 仿真结果和实际工作数据比较接近,但DEM 仿真结果比实际数据偏低,原因可能是设备的处理量和辊隙有直接关系,在破碎过程中,辊隙因受到物料的作用力而发生改变,DEM 模型无法仿真辊隙的动态变化,造成误差。

为减小误差和避免偶然性,每个模型仿真2 次,各模型预测处理量数据误差如表5所示。

表5 各模型处理量结果对比Table 5 Comparison of treatment volume results by each model

分析表5 可知,DEM-MBD 联合仿真模型预测处理量准确度最高,其次是DEM 模型,数学模型准确度最低。DEM-MBD 联合仿真模型预测值与实际测定值相比,虽然误差更小,但仍然偏低,可能是因为在实际生产中高压辊磨机辊面是柱钉面,而仿真中采取的是光滑面,降低了辊面对矿石的一部作用。在前期仿真试验过程中发现,数量大且尺寸较小的柱钉会极大增加仿真中细小单元格数量,影响仿真进度,考虑到计算机性能,在不对仿真结果造成较大误差的情况下,将柱钉辊面简化成光滑辊面。

3.3 单位能耗

在EDEM 软件中导出压辊的转矩,再利用公式(8)和(9)求得设备的单位能耗,将此结果与单位能耗数学模型求得的单位能耗,以及工业生产中的实际单位能耗数据进行对比,结果如图11所示。

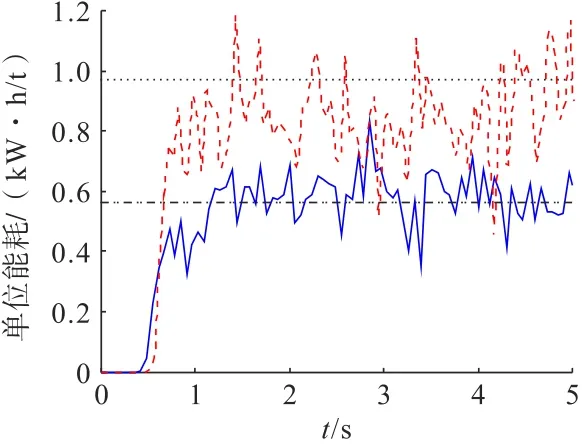
图11 各模型单位能耗曲线Fig.11 Unit energy consumption curve for each model

由图11 可以看出,DEM-MBD 联合仿真模型预测的单位能耗和实际数据拟合度非常高,DEM 仿真模型和数学模型预测值比较接近,但都比实际数据大。可能是因为在其他条件一致的情况下,单位能耗和辊隙大小成反比,辊隙越大,单位能耗越低。DEM模型和数学模型无法模拟辊隙的变化,所以造成预测值偏大。

仿真2 次,各模型预测单位能耗数据误差见表6。

表6 各模型单位能耗结果对比Table 6 Comparison of energy consumption results per unit for each model

分析表6 可知,DEM-MBD 联合仿真模型在预测单位能耗时,准确度最高,最小误差仅有3.51%,具有比较满意的结果,为后续预测单位能耗提供了一种更为准确的方式。

3.4 破碎比

表7 为各模型预测平均破碎比与实际设备测定平均破碎比的相对误差。比较表中数据,发现DEMMBD 联合仿真模型预测的平均破碎比与实际数据拟合度最好,其次是DEM 模型,但DEM 模型预测数据比实际数据要高,这是因为在高压辊磨机中,压辊通过高压将物料挤压成片,使其在辊隙中受到高压力的挤压和剪切作用。辊隙越小,物料在挤压和剪切过程中受到的力度越大,破碎效果越好,破碎产品的细度也就越高。DEM 模型没有考虑到辊隙的动态变化,一直以初始辊隙运行,所以造成破碎比偏大。

表7 各模型平均破碎比对比Table 7 Comparison of the average crushing ratio of each model

表8 分析总结了高压辊磨机各性能指标的不同模型仿真结果与实际数据的平均误差值,在初步建模阶段,应该认为仿真结果误差在一定范围内并显示正确的趋势,则DEM-MBD 联合仿真模型是成功的。

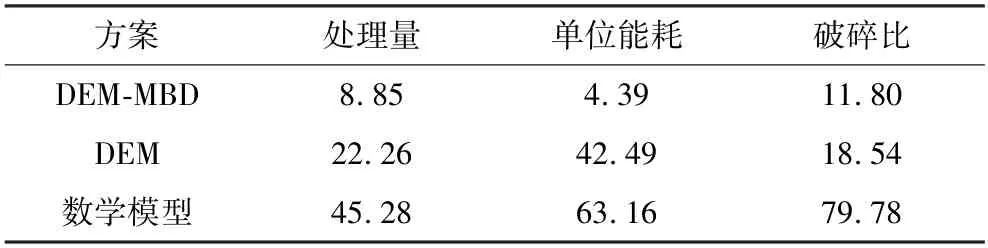
表8 各模型的性能指标相对误差Table 8 Relative error of performance indicators for each model%

4 结论

(1)以KHD375ϕ1400-1000 型高压辊磨机为研究对象,为提高高压辊磨机处理量、单位能耗、破碎比预测的准确度,本文首次将DEM-MBD 联合仿真技术应用在高压辊磨机虚拟仿真上,并详细介绍联合仿真方法和相关参数设定,研究表明DEM-MBD 仿真能够更真实地模拟设备的运行状态。

(2)为评价该联合仿真模型对高压辊磨机性能指标的预测准确度,将DEM-MBD 模型分别与DEM模型以及前文所述的处理量、单位能耗、破碎比数学模型和实际工作数据进行比较。通过对比处理量、单位能耗、平均破碎比三大性能指标,综合考虑各模型的精确度和稳定性,结果表明DEM-MBD 模型预测准确度最为理想。DEM-MBD 联合仿真模型比现有的单一DEM 仿真模型在预测处理量、单位能耗、破碎比上的误差值分别减小了13.41、38.10、6.74 个百分点。

(3)高压辊磨机DEM-MBD 联合仿真相比于DEM 仿真能够更真实、更准确地模拟设备的运行状态和性能,从而使高压辊磨机仿真模型的准确度得到显著改善,为此类仿真提供合理参考,降低了高压辊磨机的研发成本,也为高压辊磨机的设计和优化提供了更科学的依据。然而,对高压辊磨机产品粒径分布的仿真还有未尽之处,后续将针对此开展进一步研究。