考虑围岩孔隙特性的深部巷道注浆加固数值方法研究

文旭东 卢海峰,2 刘泉声,2 刘 滨 吴月秀,2

(1.武汉大学土木建筑工程学院,湖北 武汉 430072;2.岩土与结构工程安全湖北省重点实验室,湖北 武汉 430072;3.中国科学院武汉岩土力学研究所,湖北 武汉 430071;4.岩石力学与工程国家重点实验室,湖北 武汉 430071)

注浆技术是一项实用性强、应用广泛的工程技术,是改善岩土体物理力学性质,封堵地下水的有效措施,是解决煤矿深部高应力环境下泥岩巷道支护难题的必要措施[1-2]。淮南矿区是国家大型煤炭基地中的两淮基地之一,埋藏深度2 000 m 以上的煤炭资源量约500×108t,该区域由于地质构造和沉积历史,巷道围岩中泥岩或泥质胶结的岩石十分常见,整个矿区-800～-1 000 m 深度范围内约70%的岩石巷道围岩为泥岩或泥质胶结的岩石。一方面泥岩本身物理力学性质特殊,遇水极易软化,强度降低;另一方面,巷道围岩处于深部高应力环境,岩体结构复杂,裂隙水发育,因而巷道在开挖掘进过程中很难保持稳定,极易发生变形破坏,必须采取有效的支护加固措施,才能保证巷道围岩稳定和矿区安全开采。

有关注浆加固的研究,国内外学者开展了许多卓有成效的工作。在浆液扩散规律和理论模型方面,GROPPO 等[3]进行了单裂隙中浆液流动过程模拟试验,研究了浆液压力、流速等对浆液扩散半径的影响,刘嘉材[4]、石达明[5]推导出了扩散半径与注浆时间的表达式,郝哲等[6]、阮文军[7]推导了基于宾汉姆流体的浆液扩散方程,但大多数浆液在裂隙内渗流的理论都会对围岩裂隙进行简化,难以反映浆液的真实扩散情况。近年来,不少学者从注浆试验方面进行了探究,韩晓雷等[8]采用化学注浆方式对含泥粉细砂层进行注浆试验,探究了各种因素对注浆效果的影响;杨坪等[9]建立了不同粒径饱和砂砾石的注浆模型,研究了不同浆液及不同注浆压力下的浆液扩散固化机制。在注浆固结体力学特性方面,张农等[10]、刘泉声等[11]研究了注浆固结后破裂岩块残余强度的变化情况;王汉鹏等[12]开展了峰后注浆加固试件的力学特性研究;李剑等[13]、饶枭宇等[14]研究了不同配比下注浆体的物理力学性能;何真等[15]在亚微观尺度上描述了水泥石的微结构,归纳了水泥石微结构与强度的关系;詹金武等[16]、王志等[17]通过循环冲击试验研究了注浆固结体的动态特性。随着数值软件的不断更新,不少学者利用ANSYS、ABAQUS、COMSOL、FLAC 等软件,模拟了注浆过程中浆液扩散规律及注浆加固效果。李慎刚等[18]应用FLAC3D模拟了浆液在土体中的渗流过程,研究了注浆后隧道及围岩体开挖时的应力分布规律以及地表沉降情况;林元俊等[19]利用COMSOL 软件建立了软岩巷道注浆扩散瞬态计算模型和加固圈形成后的变形计算模型,对软岩巷道渗流场和位移场进行了数值模拟研究;刘浩等[20]利用FLAC3D软件模拟了注浆前后围岩未开采和开采时顶底板的位移量和塑性破坏情况。

现有的研究大多数集中浆液的扩散规律及注浆前后岩体力学特性的变化,对整体注浆效果的评价方法相对较少。本研究以淮南矿区顾北煤矿泥岩巷道注浆加固工程为例,通过注浆固结体微观结构扫描电镜试验和力学特性试验研究,对围岩孔隙特性与注浆固结体力学特性的关系进行研究,在此基础上对固结体的摩尔-库伦本构模型进行修正,并基于FLAC3D软件,开发考虑围岩孔隙特性的注浆加固评价的数值仿真分析方法,对矿区巷道群注浆加固效果进行分析计算。

1 注浆固结体力学特性试验研究

1.1 试样制备

试验选取淮南矿区顾北煤矿-648 m 水平巷道泥岩,通过碎石机将其破碎成粒径约1 cm 的碎块,按照一定的浆液水灰比及碎石配合比浇入4 个30 cm×15 cm×15 cm(长×宽×高)的长方体模具,养护1 周后,通过钻孔取芯制备成4 组不同孔隙率的圆柱形标准试样(图1),试样参数取值见表1。

表1 试样参数Table 1 Specimen parameters

图1 试样制备Fig.1 Specimen preparation

1.2 试验过程

试验在中国科学院武汉岩土力学研究所研制的RMT-150C 试验机上进行(图2),这是一种数字控制的电液伺服试验机,是专为岩石和混凝土一类材料的力学性能试验而设计的。

图2 RMT-150C 试验机Fig.2 RMT-150C test device

本研究采用RMT-150C 试验机分别对4 组不同孔隙率的注浆固结体进行单轴压缩试验,所得应力—应变全过程曲线如图3所示。

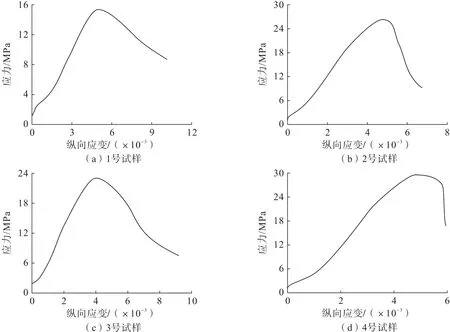
图3 单轴压缩应力—应变全过程曲线Fig.3 Complete stress-strain curves of uniaxial compression

由图3 可知:注浆固结体与一般岩石破坏过程相似,经历压密阶段、弹性变形阶段、塑性变形阶段和破坏阶段,随着孔隙率增加,注浆固结体的弹性模量逐渐增大,单轴抗压强度也呈增大趋势。值得注意的是,1～3 号试样在达到峰值应力后还呈现出应变软化和残余阶段,孔隙率最大的4 号试样则呈现出明显的脆性破坏。

对4 组不同孔隙率试样分别进行了不同围压等级下的三轴试验,围压等级分别为0、2、5、10、20 MPa,试验得到的应力—应变全过程曲线如图4所示。

图4 三轴压缩应力—应变全过程曲线Fig.4 Complete stress-strain curves of triaxial compression

由图4 可知:相同围压下,随着孔隙率增加,注浆固结体峰值应力逐渐增加;随着围压增加,注浆固结体的残余强度逐渐增加,且破坏模式逐渐向延性破坏转变。

1.3 力学特性分析

1.3.1 强度特性分析

根据试验数据,分别绘制了4 组试样的摩尔圆(图5),得到不同孔隙率条件下注浆固结体的强度参数,见表2。

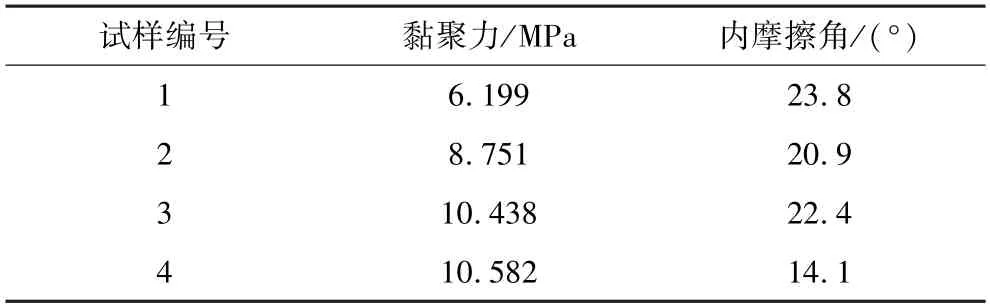
表2 注浆固结体强度参数Table 2 Strength parameters of grouting consolidation bodies

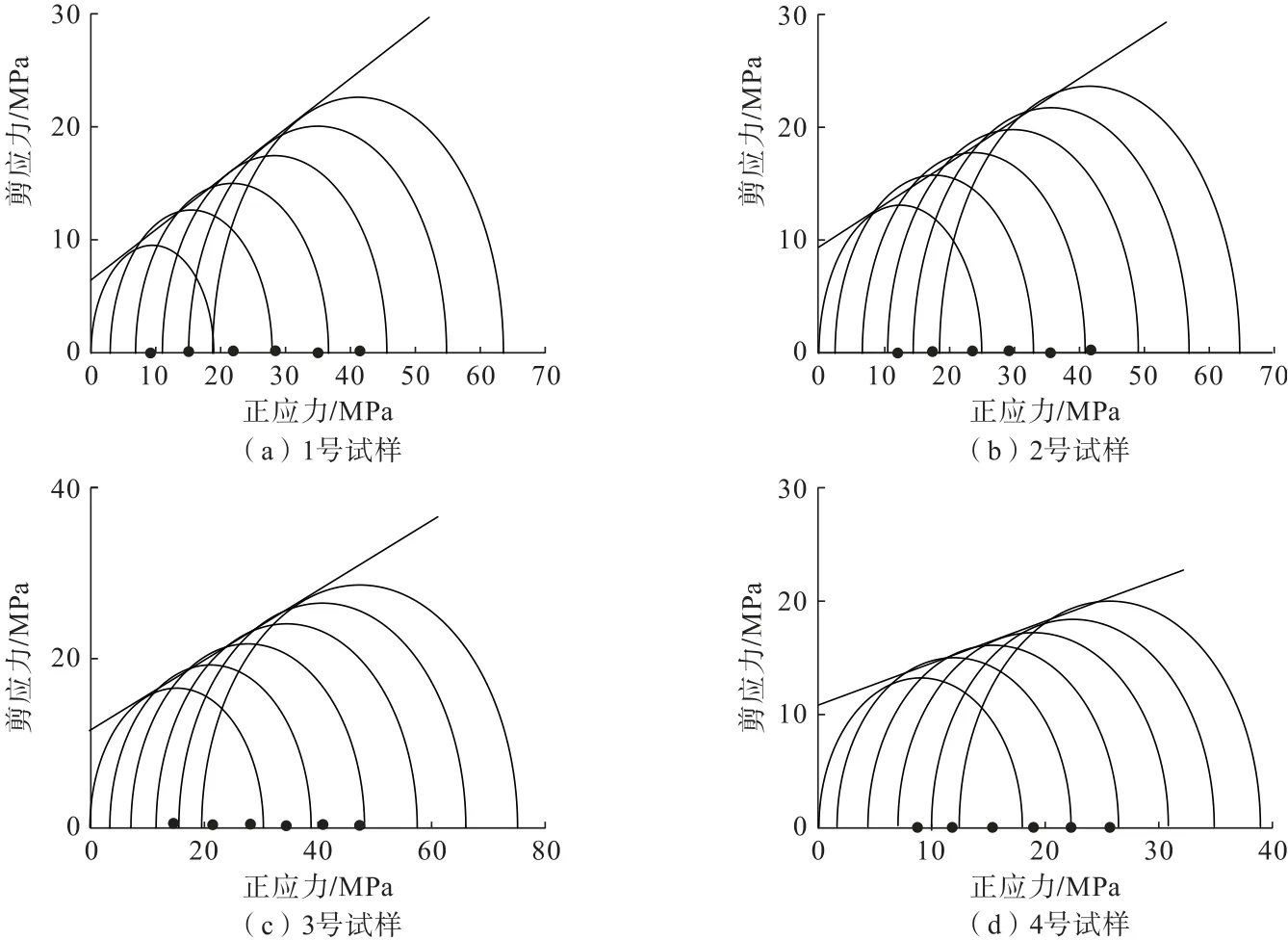
图5 三轴试验摩尔圆Fig.5 Triaxial test molar circle

由表2 可知:注浆固结体的黏聚力随着孔隙率增大呈增长趋势,符合对数函数关系,内摩擦角随孔隙率增大而减小(图6、图7)。

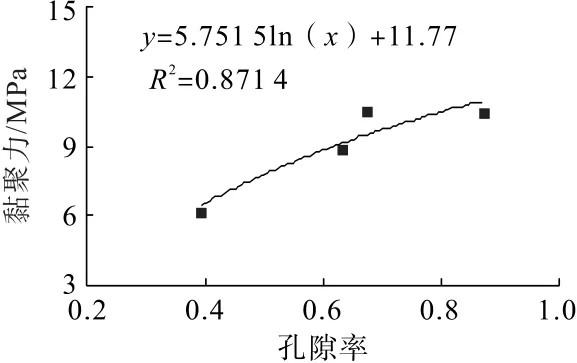
图6 黏聚力与孔隙率的关系Fig.6 Relationship between cohesion and porosity

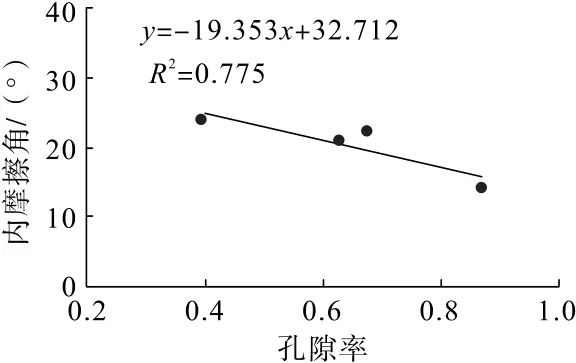
图7 内摩擦角与孔隙率的关系Fig.7 Relationship between internal friction angle and porosity

1.3.2 变形特性分析

孔隙率与注浆固结体弹性模量和泊松比的关系如图8、图9所示。由图8、图9 可知:弹性模量随着孔隙率的增大呈对数函数增长,而泊松比变化规律不明显,取值范围为0.18～0.23。

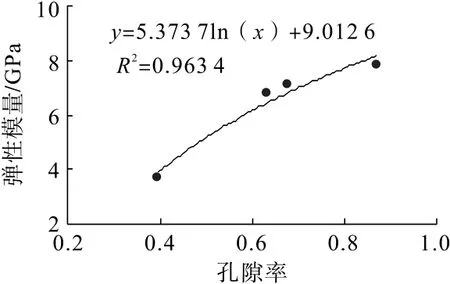
图8 弹性模量与孔隙率的关系Fig.8 Relationship between elastic modulus and porosity

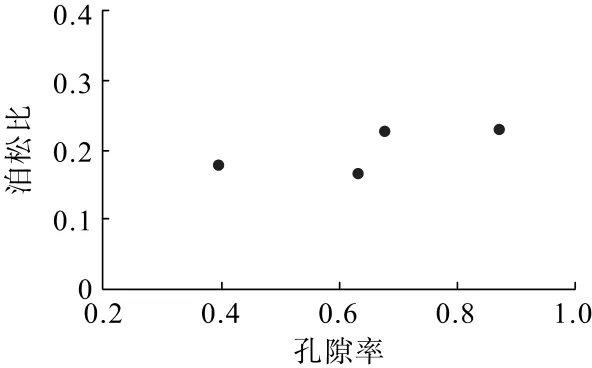
图9 泊松比与孔隙率的关系Fig.9 Relationship between poisson′s ratio and porosity

1.4 注浆固结体胶结特性

注浆固结体的力学特性与其微观结构存在一定联系,为了研究注浆固结体的微观胶结特性,分别对4 种注浆固结体在Quanta 250 型环境电子扫描显微镜上进行观察,得到了不同放大倍数下注浆固结体的微观图片,如图10 至图13所示。

图10 1 号试样扫描电镜图Fig.10 Scanning electron microscope chart of No.1 sample

图11 2 号试样扫描电镜图Fig.11 Scanning electron microscope chart of No.2 sample

图12 3 号试样扫描电镜图Fig.12 Scanning electron microscope chart of No.3 sample

图13 4 号试样扫描电镜Fig.13 Scanning electron microscope chart of No.4 sample

由图10 至图13 可知:在较小放大倍数下,浆液与岩石接触面接触都很好,但随着放大倍数增加,可以看出不同孔隙率试样中浆液与岩石的接触关系不同。1 号试样孔隙率最小,通过其2 000 倍放大图(图10(d))可以看出,浆液与岩石之间并没有完全解除,存在一定的微观裂缝。随着岩石孔隙率增加,岩块被更多的浆液所包裹,浆液与岩石接触面胶结越好,浆液与接触面之间微裂隙越小,当孔隙率增大到一定程度时,浆液与接触面互相融合,胶结效果最好(图13)。

结合注浆固结体微观结构特征,可以将注浆固结体分为两种胶结模式:一种为包裹模式,另一种为搭接模式(图14)。包裹模式往往出现在岩体孔隙率较大时,浆液充填范围较大,对岩石块体形成包裹,这种模式下浆液与岩石块体胶结紧密。搭接模式往往出现在岩体孔隙率较小时,此时浆液可充填范围相对较小,浆液主要相邻岩石块体起到黏结作用,岩石块体与浆液之间胶结相对较弱。

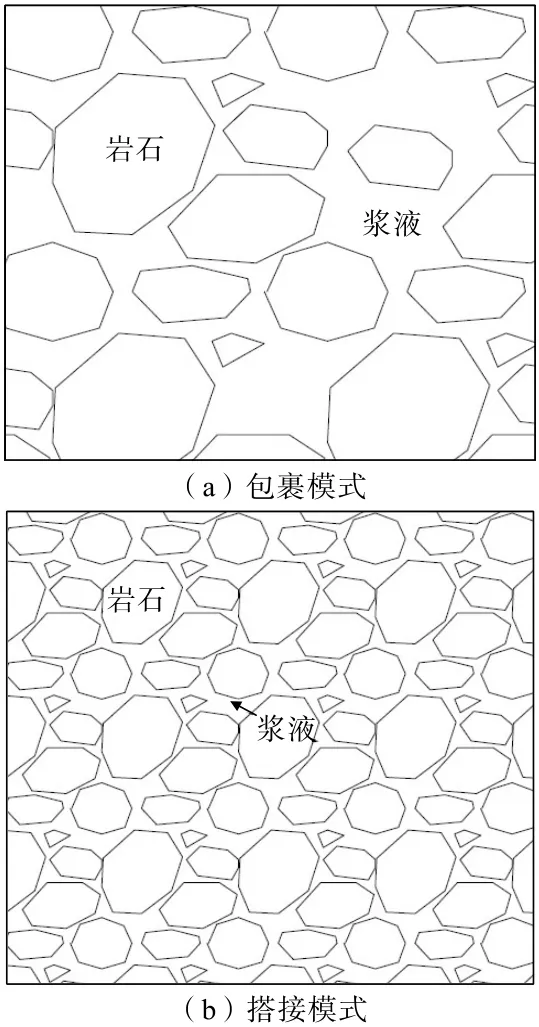
图14 注浆固结体胶结模式Fig.14 Cementing modes of grouting consolidation body

注浆固结体的胶结模式与其力学特性有着密切联系,包裹模式下的注浆固结体其力学特性接近水泥石的力学特性,由于浆液黏结作用强烈,使得岩体发生破坏所需的起始作用力较大,反映到力学参数上就是黏聚力较大,而搭接模式下的注浆固结体由于浆液充填相对较少,黏结作用相对较弱,所以黏聚力也相对较小。内摩擦角大小反映了岩体发生破坏形成贯通破裂面的难易程度,在搭接模式下,由于岩石碎块分布较多,而岩石块体的强度相对较大,所以在破坏面形成过程中受到岩块阻挡,形成贯通破坏面所需的力相对较大,从而使得注浆固结体内摩擦角较大。在包裹模式下,岩块含量相对较少,对破裂面形成路径的阻挡影响较少,破裂面形成所需的力相对较小,使得注浆固结体的内摩擦角相对较小。这些特性在上述固结体力学特性试验中也很好地反映出来。

2 注浆固结体本构模型研究

2.1 水泥石强度试验

岩体注浆后,浆液充填裂隙或包裹碎裂块体,一方面提高了岩体的弹性模量,影响岩体的应力—应变关系;另一方面对岩体强度参数产生影响,从而影响了岩体的屈服准则。这两方面特性的改变使得注浆固结体的本构模型发生改变。为了进一步研究注浆固结体与水泥石之间的强度和变形关系,依据上述注浆固结体试验所用水灰比(表1),制备了不同龄期的圆柱形试样,并分别进行了单轴压缩试验和三轴压缩试验,试验结果见表3 和表4。

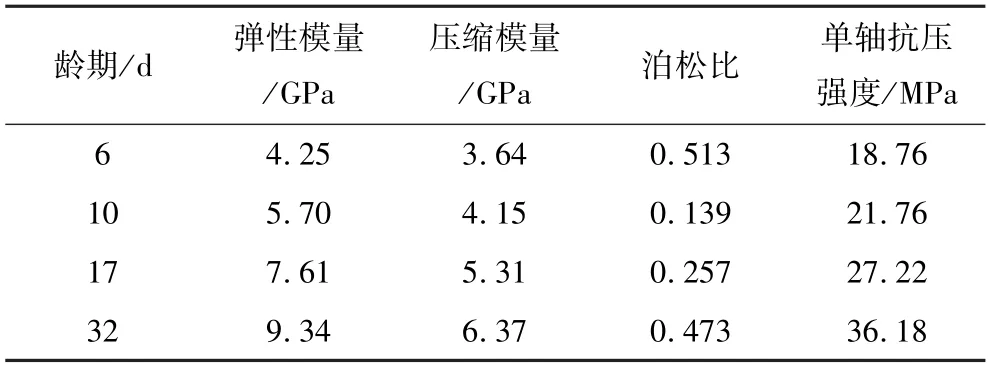
表3 单轴压缩试验结果Table 3 Uniaxial compression test results

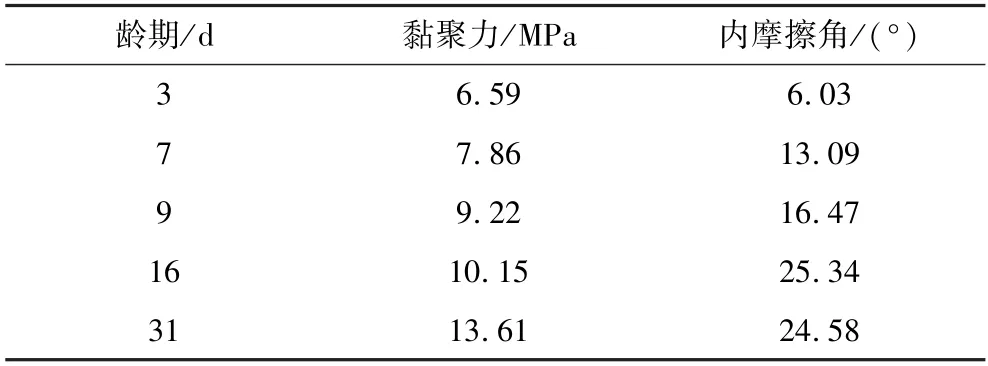
表4 三轴压缩试验结果Table 4 Triaxial compression test results

2.2 模量修正

式中,Eg为注浆固结体的弹性模量,GPa;β为岩体孔隙率或裂隙率;a和b为影响系数。

假定岩体裂隙或孔隙在被浆液充满的理想状态下,若孔隙率或裂隙率β=1 时,则式(1)中所得弹性模量实际为纯浆液固结形成的水泥石的弹性模量。于是,式(1)可进一步表示为

式中,E0为水泥石的弹性模量,GPa。

由表3 可得到水泥石弹性模量和龄期之间存在以下关系:

式中,t为注浆固结时间,d;e和f为影响系数。

联立式(2)、式(3)可以得到:

9、《关于进一步落实重点群体创业就业税收政策的通知》。11月23日，为支持和促进重点群体创业就业，财政部、税务总局、人力资源社会保障部财政部等三部门下发《关于进一步落实重点群体创业就业税收政策的通知》（财税〔2018〕136号），就政策落实提出具体要求。

式(4)即为修正后的注浆固结体弹性模量表达式,可见注浆固结体的弹性模量是与岩体裂隙率或孔隙率以及注浆固结时间相关的量,其影响系数a、e和f等参数取值取决于浆液性质。

2.3 强度修正

由图6 和图7 得到注浆固结体的黏聚力和内摩擦角与岩体孔隙率之间分别满足以下关系:

式中,Cg为注浆固结体的黏聚力,MPa;φg为注浆固结体的内摩擦角,(°);β为岩体的孔隙率或裂隙率;m、n、l和p为影响系数。

与上述模量修正类似,当孔隙率或裂隙率β=1时,所得强度参数为纯浆液固结形成的水泥石强度参数,即:

由表3 可知,水泥石的强度参数与龄期之间存在以下关系:

式中,t为龄期,d;h、n、k、j为影响系数。

联立式(5)、式(6),并代入(7)可得:

式(8)即为修正后的注浆固结体强度参数表达式。

2.4 本构模型修正

结合前文对注浆固结体模量和强度特征的研究,对岩石力学中最常用的摩尔-库伦本构模型进行修正,主要是对模型中模量参数和强度参数的修正。

2.4.1 修正的增量弹性定律

经过模量修正,应力-应变本构关系增量表达式可表示为

式中,参数α1、α2计算公式为

式中,β为岩石孔隙率;t为注浆固结时间,d;v为泊松比;a、e、f为影响系数,由试验确定。

2.4.2 修正的屈服函数

由Mohr-Coulomb 屈服函数破坏包络线公式为

式中,β为内摩擦角,(°);C为黏聚力,MPa;Nφ为材料参数。

将式(8)代入式(11)可得:

式中,m、h、n、k、p、j为影响系数,可由室内试验获取。

3 深部巷道群注浆加固数值仿真计算分析

通过FLAC3D软件自定义本构模型功能,将上述修正后的摩尔-库伦本构模型写入程序,调试后以淮南矿区顾北煤矿为工程背景进行注浆固结体数值仿真计算分析。

3.1 工程概况及模型构建

淮南矿区顾北煤矿南翼11-2 采区胶带机巷、轨道巷和矸石胶带机巷为3 条平行巷道(图15),均穿越F104-1、FD104-1、F93-1 等多条断层,受构造带影响,断层附近区域围岩破碎,裂隙发育。断层带宽度为25～30 m,断层带内岩层破碎,岩性以泥岩为主,含少量砂质泥岩,遇水软化。巷道掘进先后顺序为胶带机巷、轨道巷和矸石胶带机巷,以这3 条巷道为例,运用前面所建立的注浆固结体数值仿真分析模型,对巷道开挖过程的应力和变形规律,以及注浆固结效果进行计算分析。

图15 巷道平面Fig.15 Roadway plan

本研究构建的模型长120 m、宽30 m、高60 m。模拟时采用全断面开挖方式,开挖次序按照实际工程中巷道布置为从左到右,即胶带机巷、轨道巷和矸石胶带机巷。模型共有28 080 个单元,30 681 个节点,如图16所示。

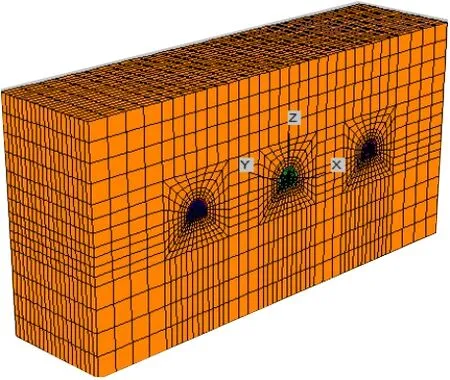
图16 计算模型Fig.16 Calculation model

3.2 计算方案

选取本研究上述试验中所使用的水灰比(0.4),分别进行巷道无注浆条件下的开挖过程分析以及巷道依次注浆过程分析。注浆区域划分为3 个不同孔隙率区域,巷道外围3 m 范围内岩体较破碎,采用较大孔隙率(0.5),外围3～7 m 范围采用0.3 的孔隙率,其他区域按原岩条件处理,注浆范围分布如图17所示。

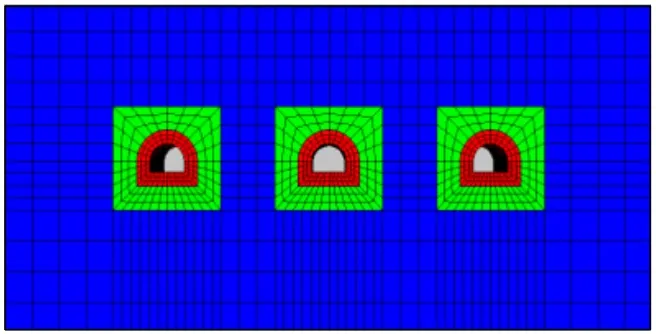
图17 注浆加固范围Fig.17 Scope of grouting reinforcement

3.3 无注浆条件下巷道开挖计算分析

3.3.1 应力分布

3 条巷道应力分布如图18 至图20所示。分析可知:胶带机巷开挖后应力调整,在巷道顶部、帮部以及底脚最大主应力(σ1)最大,而最小主应力(σ3)最小,两者应力差在顶部、帮部和底脚最大,使得巷道在顶部和两帮易发生破坏,产生较大变形。巷道底部最大主应力和最小主应力均比其他部位小,出现应力薄弱区,这也是巷道易产生底鼓变形的主要原因;其他巷道开挖后也呈现出上述规律。

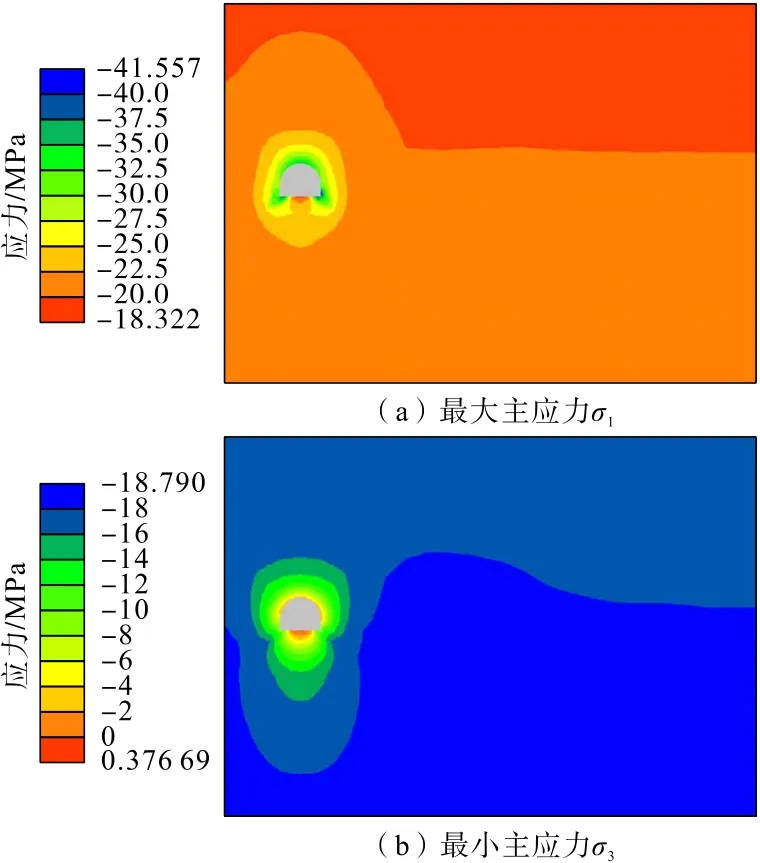
图18 胶带机巷开挖后应力分布Fig.18 Stress distribution of belt conveyor roadway after excavation

图19 轨道巷开挖后应力分布Fig.19 Stress distribution of track roadway after excavation

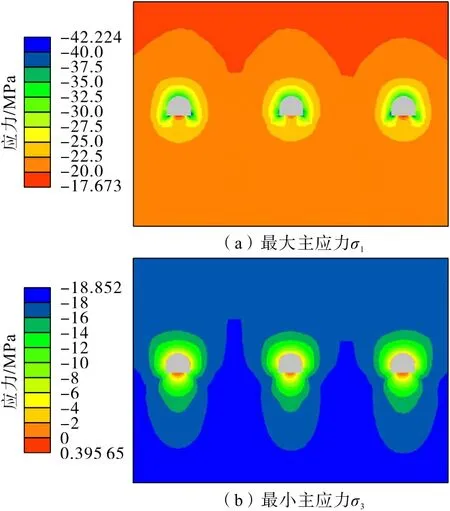
图20 矸石胶带机巷开挖后应力分布Fig.20 Stress distribution of gangue belt conveyor roadway after excavation

3.3.2 位移分布

3 条巷道开挖后的位移分布如图21所示。分析可知:胶带机巷开挖后,巷道表面位移最大,其中拱顶下沉位移、两帮收敛位移以及底鼓位移最为明显,这与前述应力分布规律分析结果相适应;邻近轨道巷和矸石胶带机巷开挖后也呈现出相同的变形规律,且相邻巷道应力叠加区域的位移分布发生变化。

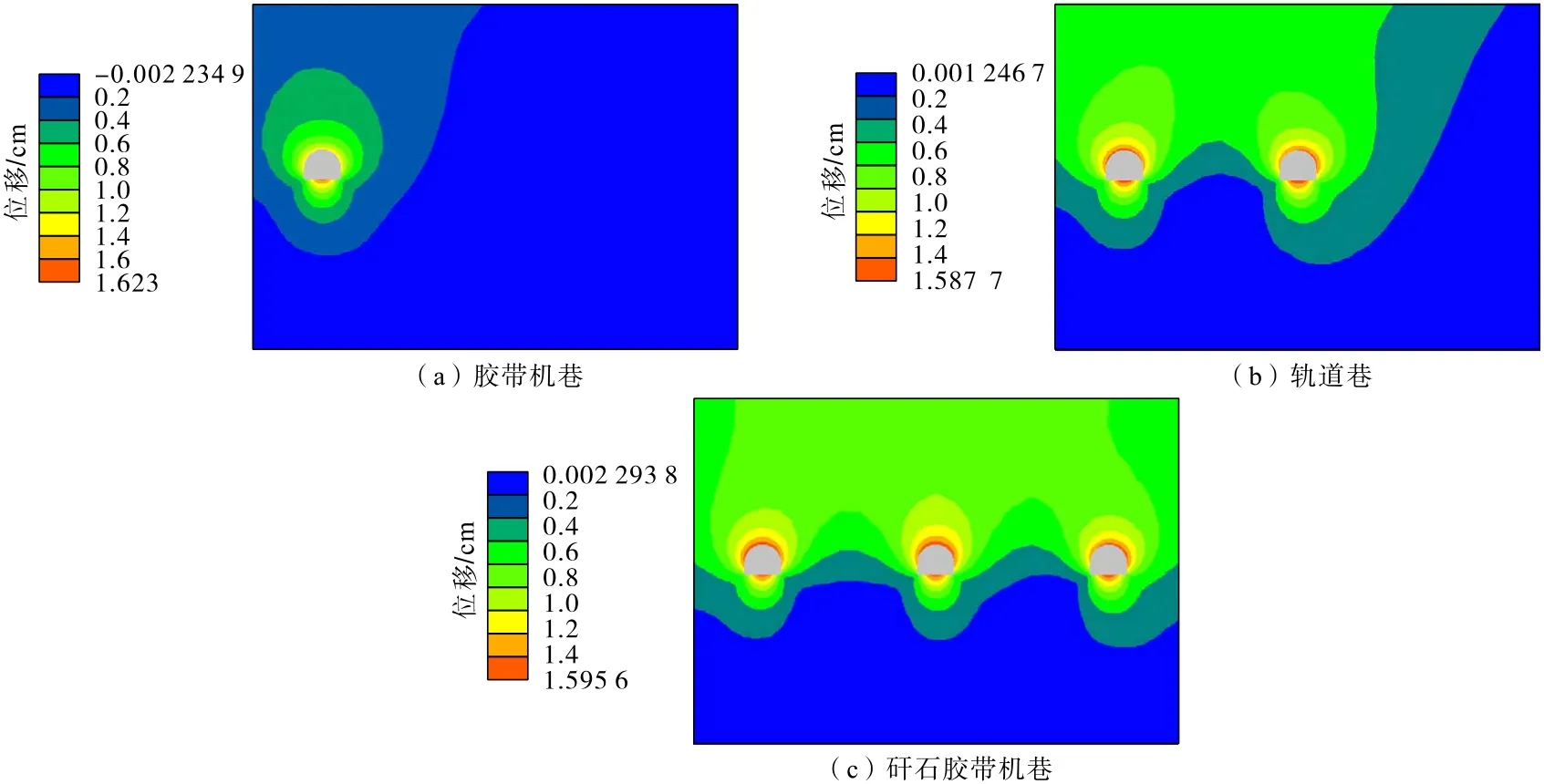
图21 3 条巷道开挖后位移分布Fig.21 Displacement distribution the three roadways after excavation

3.4 注浆条件下巷道开挖计算分析

煤矿深部巷道开挖后围岩发生变形,顶板下沉、两帮收敛和底鼓是巷道变形最主要的表现形式,分步联合支护方法和底板锚索治理是控制巷道变形的有效措施,然而这些方法和措施能够有效发挥作用的关键在于注浆加固对围岩的修复作用。为了研究注浆过程中巷道围岩应力及变形规律,在不施加其他支护措施情况下,本研究对单纯注浆条件下的巷道围岩应力和位移进行计算分析。按照巷道施工工序,依次对胶带机巷、轨道巷和矸石胶带机巷开挖注浆后7、14、30 d 的巷道围岩应力和位移进行了计算,以注浆后7 d 和30 d 效果为例进行对比分析。

3.4.1 胶带机巷注浆过程计算结果

胶带机巷开挖注浆7 d 和30 d 后的应力分布如图22 和图23所示。分析可知:胶带机巷开挖注浆初期,最大主应力在巷道外围形成环形应力集中,随着注浆时间增加,最大主应力逐渐向内外两侧转移,最终形成与未注浆条件下相似的应力分布。巷道周围最小主应力范围也随着注浆时间增加而减小。应力分布的这一变化过程较为真实地反映了围岩随时间的应力转移过程,开挖初期,巷道周围岩体破碎,承载能力较低,其应力通过围岩变形来释放,四周围岩传递过来的应力主要靠更深部的岩体承担。随着浆液固结时间增加,洞周围岩体强度增加,抗变形能力也增大,能够承受四周围岩体传递过来的应力,且变形也能够得到有效控制。

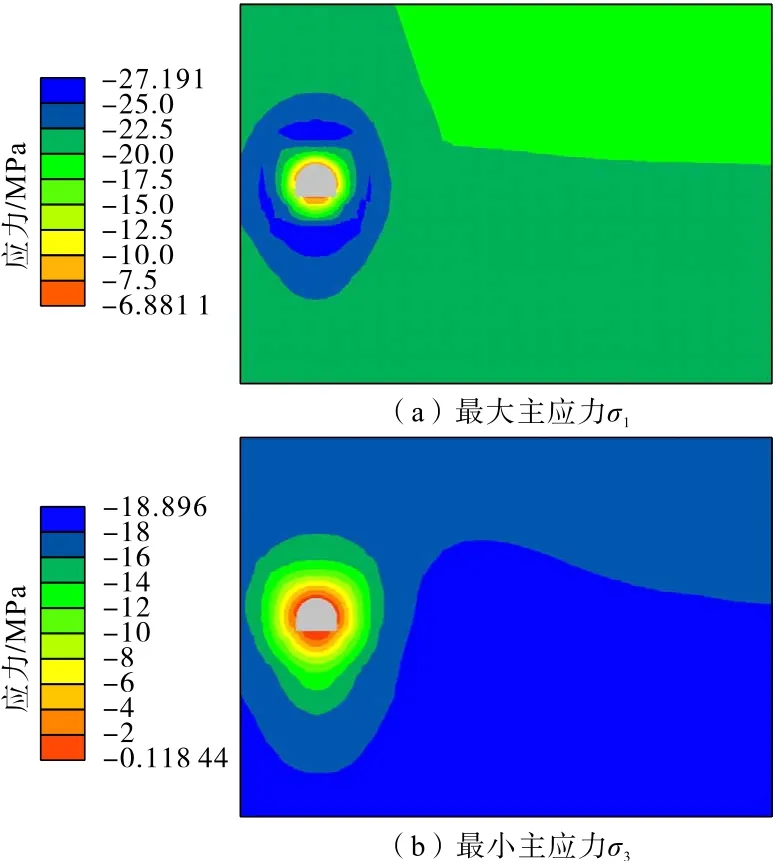
图22 胶带机巷开挖注浆(7 d)应力分布Fig.22 Stress distribution of belt conveyor roadway after excavation grouting(7 days)

图23 胶带机巷开挖注浆(30d)应力分布Fig.23 Stress distribution of belt conveyor roadway after excavation grouting(30 days)

胶带机巷开挖注浆后的总位移分布如图24所示。该图显示的位移分布与前述应力分布相适应,胶带机巷开挖注浆初期巷道围岩最大变形主要在洞壁,主要为拱顶下沉、两帮收敛和底鼓,随着注浆固结时间增加,围岩变形逐渐减小。

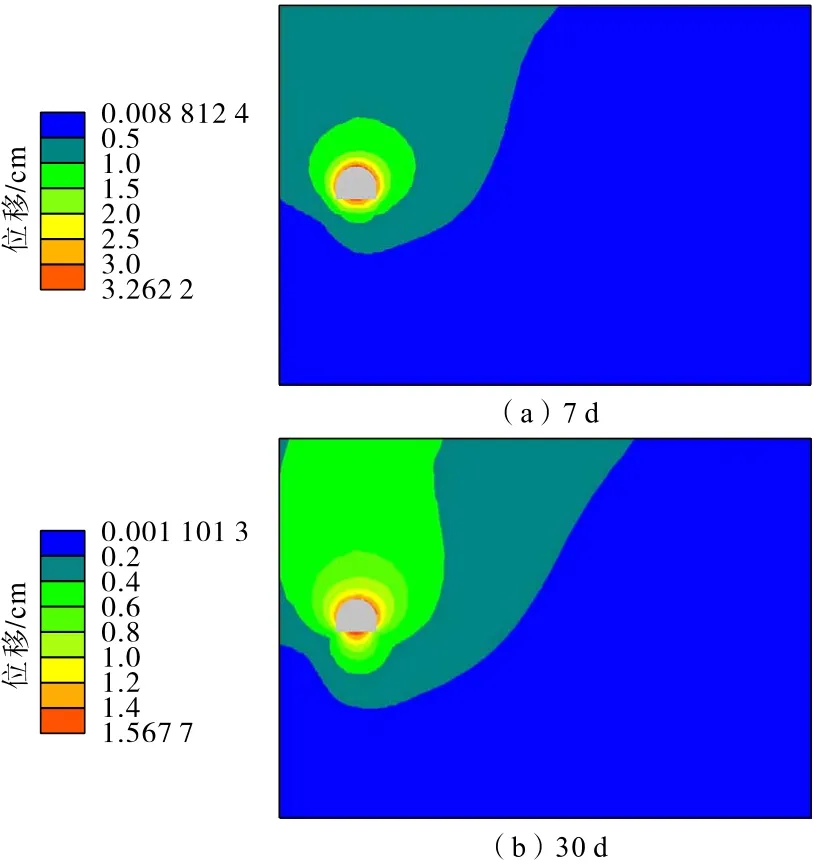
图24 胶带机巷开挖注浆后总位移分布Fig.24 Total displacement distribution of belt conveyor roadway after excavation and grouting

3.4.2 轨道巷注浆过程计算结果

轨道巷开挖注浆7 d 和30 d 后的应力分布如图25 和图26所示。分析可知:轨道巷开挖注浆初期,巷道围岩最大主应力主要集中在左侧已开挖注浆的胶带机巷周围,轨道巷周围最大主应力相对较小,随着注浆时间增加,轨道巷周围注浆固结体强度增大,所承担的最大主应力也逐渐增加,最终在两条巷道周围达到平衡。

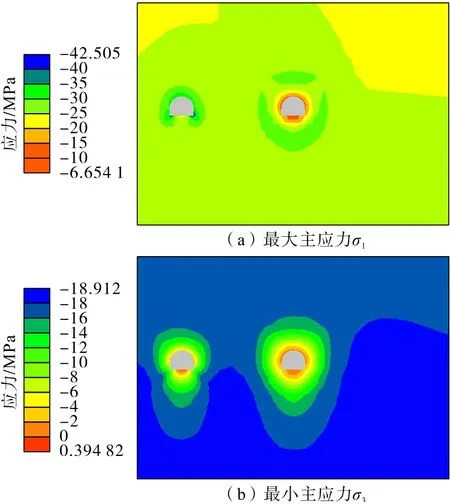
图25 轨道巷开挖注浆(7 d)应力分布Fig.25 Stress distribution of track roadway after excavation grouting(7 days)

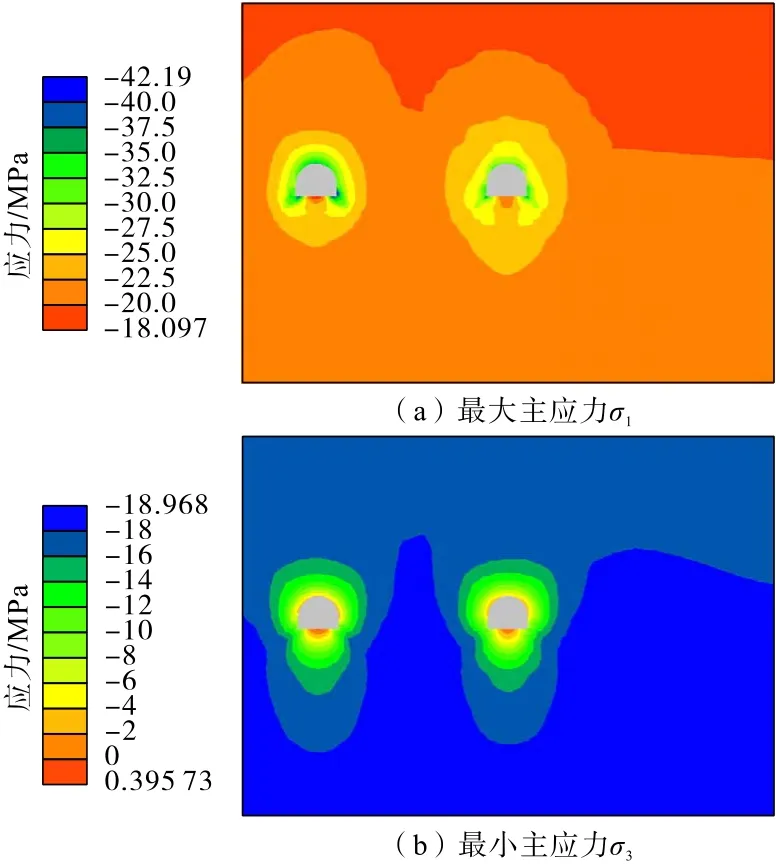
图26 轨道巷开挖注浆(30 d)应力分布Fig.26 Stress distribution of track roadway after excavation grouting(30 days)

轨道巷开挖注浆初期,巷道周边岩体位移较大,随着注浆固结时间增加,应力在巷道之间调整,位移也逐渐向已经注浆加固完成的胶带机巷转移,最后在胶带机巷周围岩体位移达到最大值,但位置总是比无注浆条件下巷道位移要小很多(图27)。

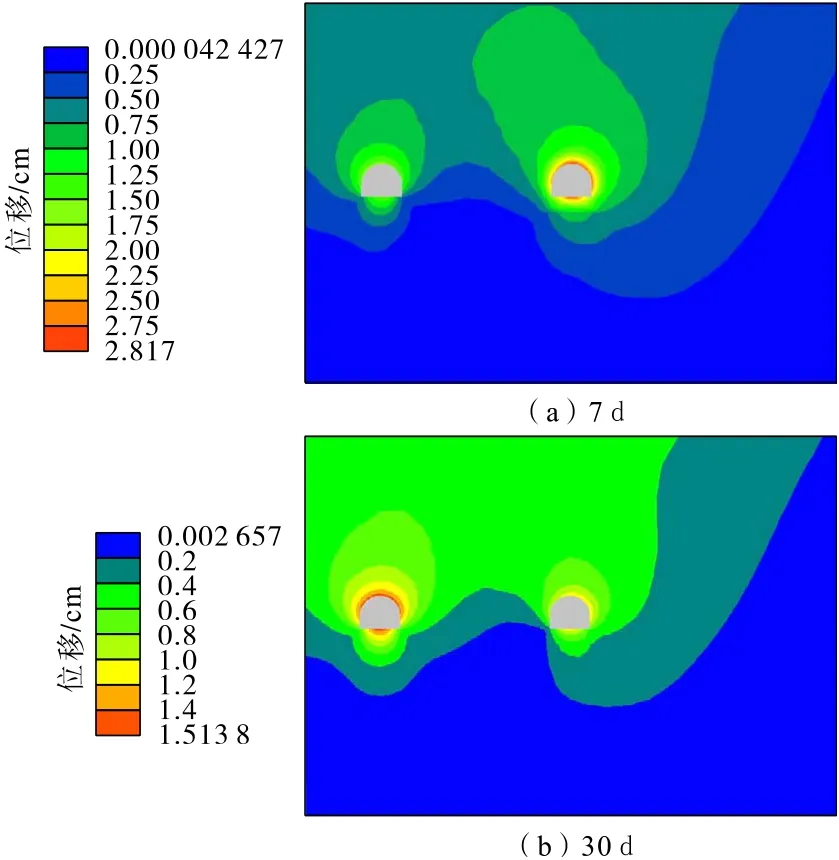
图27 轨道巷开挖注浆后总位移分布Fig.27 Total displacement distribution of track roadway after excavation grouting

3.4.3 矸石胶带机巷注浆过程计算结果

矸石胶带机巷开挖注浆7 d 和30 d 后的应力分布如图28 和图29所示。分析可知:矸石胶带机巷开挖过程应力分布规律与轨道巷相似,在开挖注浆初期,巷道围岩最大主应力主要集中在左侧已开挖注浆的轨道巷和胶带机巷周围,矸石胶带机巷周围最大主应力相对较小,随着注浆时间增加,矸石胶带机巷周围注浆固结体强度增大,所承担的最大主应力也逐渐增加,最终3 条平行巷道周围应力达到动态平衡。

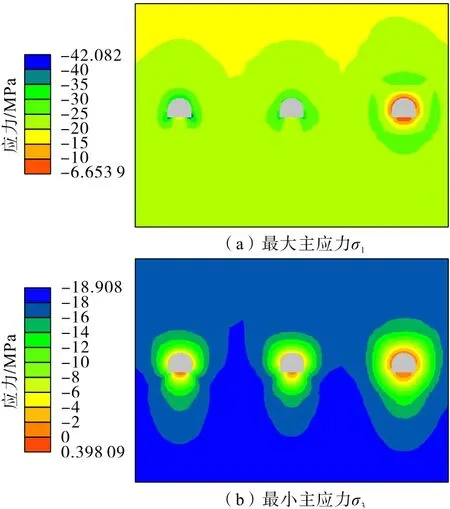
图28 矸石胶带机巷开挖注浆(7 d)应力分布Fig.28 Stress distribution of gangue belt conveyor roadway after excavation grouting(7 days)

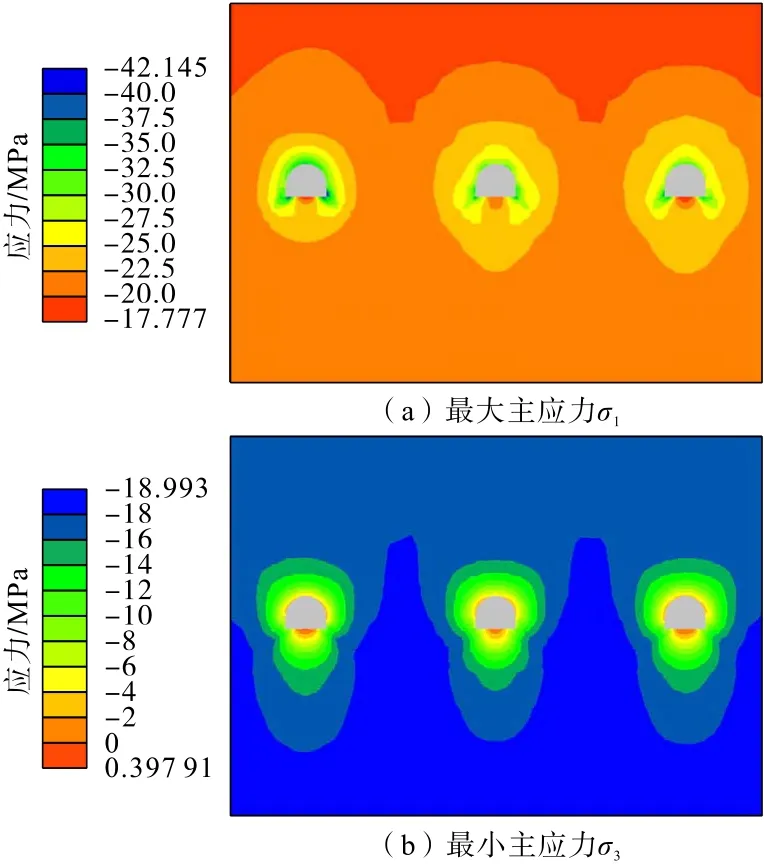
图29 矸石胶带机巷开挖注浆(30 d)应力分布Fig.29 Stress distribution of gangue belt conveyor roadway after excavation grouting(30 days)

巷道开挖注浆初期,巷道周边岩体位移较大,随着注浆固结时间增加,应力在巷道之间调整,位移也逐渐向已经注浆加固完成的胶带机巷和轨道巷转移,最后在胶带机巷周围岩体位移达到最大值,轨道巷周边位移次之,矸石胶带机巷周边位移最小(图30)。与无注浆条件下巷道开挖后位移相比,3 条巷道位移值均大大减小,可见注浆加固对巷道围岩变形控制起到了显著作用。可见,本研究所提出的考虑围岩孔隙特性的注浆加固评价的数值仿真分析方法能够有效模拟巷道围岩注浆加固效果。

图30 矸石胶带机巷开挖注浆总位移分布Fig.30 Total displacement distribution of gangue belt conveyor roadway after excavation grouting

4 结论

以淮南矿区顾北煤矿深部巷道围岩注浆加固工程为例,对煤矿深井巷道注浆固结体的力学特性进行了分析研究,在此基础上对摩尔-库伦本构模型进行修正,开发了适合进行注浆加固评价的数值分析方法。所得到结论如下:

(1)孔隙率对注浆固结体的强度和变形特性影响较大。随着孔隙率增加,注浆固结体的弹性模量逐渐增大,单轴抗压强度也呈增大趋势;相同围压下,随着孔隙率增加,注浆固结体峰值应力逐渐增加;随着围压增加,注浆固结体的残余强度逐渐增加,且破坏模式逐渐向延性破坏转变。注浆固结体的黏聚力随着孔隙率的增大呈增长趋势,符合对数函数关系;而内摩擦角随孔隙率增大而减小。

(2)注浆固结体主要包括包裹和搭接两种胶结模式。注浆固结体的力学特性与其胶结模式之间存在密切联系。

(3)以摩尔-库伦模型为基础,通过模量修正和强度修正,建立了适合注浆固结体的修正的摩尔-库伦本构模型,并通过FLAC3D软件自定义本构模型功能,建立了煤矿深部巷道注浆加固数值分析方法。该方法能有效反映煤矿深部巷道注浆加固过程中的应力和位移变化特征,可为煤矿深部巷道注浆加固设计和施工提供分析评价方法。