基于IFOA-RotGBM的矿用挖掘机发动机故障诊断

2023-10-19顾清华孙文静李学现

金属矿山 2023年9期

顾清华孙文静李学现

(1.西安建筑科技大学资源工程学院,陕西西安 710055;2.西安市智慧工业感知计算与决策重点实验室,陕西西安 710055;3.西安建筑科技大学管理学院,陕西西安 710055)

随着“中国制造2025”战略的提出,矿山机械设备故障诊断技术逐步向智能化方向发展,但由于复杂设备故障模式的多样化,现阶段设备故障诊断仍难以实现智能精准识别[1]。挖掘机是集机械、电子控制、液压等技术于一体,自动化程度高的大型工程施工装配,在矿山采掘作业中承担着重要作用[2]。由于矿山恶劣复杂、高强度、高负荷的作业环境以及日常维修不当,其发动机极易发生磨损甚至致命故障,进而导致停机。如果故障不及时诊断,不仅影响矿山既定的生产计划,给企业带来经济损失,严重时还会威胁人身安全[3]。因此,对矿用挖掘机发动机故障进行快速诊断,精准定位故障点,实现早期预警,对保障矿山安全高效开采以及实现经济效益最大化至关重要。

目前对挖掘机的故障诊断研究大都集中于对液压系统的诊断,对发动机的诊断研究相对匮乏[4-5]。由于挖掘机体型较大,各系统组成之间故障关联性较强,导致大多数发动机故障具有一定的复杂性和隐蔽性。虽然目前国内几大重工企业都上线了远程监控与诊断平台,但是智能化程度较国外差距很大,很多故障仍需依赖工程师停机诊断,导致诊断精度和效率很低[6],所以寻找一种鲁棒精确的故障识别方法作为辅助很有必要。为了提高诊断精度,各种基于人工智能的复杂机械设备故障诊断方法被应用到发动机故障诊断中,如神经网络[7]、支持向量机[8]、深度学习[9]、随机森林[10]等。张攀等[7]针对角加速度分析法对于发动机单缸失火诊断的局限性,提出一种将瞬时转速信号和人工神经网络相结合的发动机失火诊断方法。本研究团队[8]为了提高矿用卡车发动机的故障检测精度,提出一种基于CSSA 参数优化的FSVM 模型对矿用卡车发动机进行故障预测。白雲杰等[9]针对柴油机缸盖振动信号非线性特点,提出一种改进变分模态分解和深度神经网络相结合的柴油机混合故障诊断方法。魏东海等[10]提出将小波包分解和随机森林相结合用于发动机故障预测,该方法比单一分类器能更准确地诊断出柴油机的故障状态。上述方法对于提升故障诊断精度发挥了一定的作用,但由于算法本身的不足导致诊断方法存在一定的局限性。例如SVM、神经网络等都属于单一分类器,存在泛化能力弱、过拟合等问题;深度学习算法虽然特征信息提取方便,但训练时间很长,不利于故障诊断的及时性;随机森林模型虽然泛化能力强,但是其训练受决策树数目影响,在噪声较大的数据集上容易过拟合。

基于随机森林中随机性注入可以提高分类精度的思想,RODRIGUEZ 等[11]提出了旋转森林(Rotation Forest,RotForest)算法,利用主成分分析(PCA)来转换原始特征空间,以促进基分类器间的多样性来提高分类精度。然而旋转森林需要执行多个PCA 计算来生成旋转特征空间,存在一定的训练耗时。LightGBM 作为一种新的集成学习框架,不仅具有较快的训练速度,而且分类性能也很好。但LightGBM 的超参数很多,存在较大的不确定性,对分类精度有很大影响。文献[12-13]分别选用PSO、GWO 算法对Light-GBM 进行参数寻优,但这些算法存在收敛速度慢、易陷入局部极值等不足,影响了LightGBM 的分类性能。

针对以上问题,本研究提出了一种基于改进果蝇算法优化RotGBM的矿用挖掘机发动机故障诊断方法。首先通过RF-RFE 方法对发动机的故障数据进行特征提取,减少不必要的资源消耗。其次从两个方面对旋转森林进行改进生成RotGBM 分类模型。然后考虑到LightGBM 中超参数的不确定性会给故障诊断结果带来很大影响,选用改进的果蝇算法对Light-GBM 的重要超参数进行优化,构建最终的IFOA-Rot-GBM 故障诊断模型,实现挖掘机发动机故障的快速精准诊断。

1 理论基础

1.1 RF-RFE 特征提取

RF-RFE 算法由随机森林(Random Forest,RF)和递归特征消除(Recursive Feature Elimination,RFE)两者构成[14]。该方法先通过RF 对故障数据计算特征重要性并排序;然后用RFE 算法迭代剔除重要性较小的特征,最终得到一个特征数量最少、分类性能最好的发动机故障特征集[15]。

1.2 旋转森林

旋转森林的总体思想是利用PCA 旋转原始特征轴,将不同的训练集分配给每个基分类器,以促进多样性。通过保留全部主成分训练基分类器来寻求准确性。

假定有一个数据集H=[X,Y],其中X={x1,x2,…,xm}是一个具有m个样本和n个特征的训练集,Y={y1,y2,…,ym}表示训练集X对应的类标签。用D1,…,Di,…,DL表示L个基分类器,F代表特征集,则该模型的训练步骤为:首先,将F随机分成k个子集,每个子集都具有r(r=F/k)个特征;其次,对于每个特征子集Fij(j=1,2,…,k),提取相应的样本子集进行重采样,然后将PCA 应用到该样本子集上得到新样本子集;重复上述步骤,得到多个新样本子集,并在新样本子集上建立基分类器Di(i=1,2,…,L);最后集成这L个基分类器,得到最终的旋转森林模型。

1.3 LightGBM

LightGBM 是一种新的基于GBDT 的集成学习框架,主要针对现有的GBDT 和XGBoost 在节点分裂准则和解决高维问题方面存在不足而提出的[16]。相比于GBDT 和XGBoost,LightGBM 分别采用基于梯度的单边采样(GOSS)和互斥特征绑定(EFB)技术来处理大规模数据样本和高维特征,并基于直方图算法寻找最优特征分割点,再通过具有深度限制的leaf-wise 策略生成决策树。LightGBM 还支持投票并行、数据并行和特征并行,在保证准确率的同时大大提升了训练速度。

2 基于IFOA 优化的RotGBM 故障诊断模型

2.1 RotGBM 模型

根据RotForest 基本原理分析可知,训练一个RotForest 模型比较耗时。本研究从降低PCA 的计算复杂度和整个模型训练时PCA 的计算次数两个方面对旋转森林进行改进。RotGBM 算法框架如图1 所示。RotGBM 保留了原始RotForest 的主要结构,但也增加了一些变化来减少训练时间。

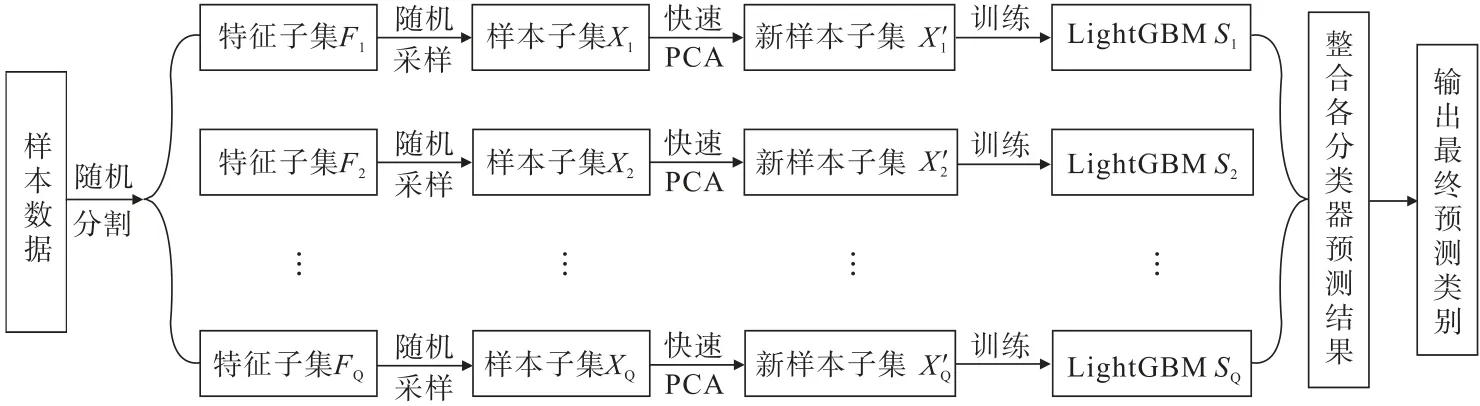
图1 RotGBM 算法框架Fig.1 Framework of RotGBM algorithm

2.1.1 PCA 计算复杂度降低策略

传统的PCA 需要先计算特征的协方差矩阵,然后对其分解得到旋转矩阵。当数据维数较高时,分解协方差矩阵的计算量很大,消耗大量的计算时间。而奇异值分解(SVD)则可以直接对特征矩阵进行分解得到旋转矩阵,无需计算协方差矩阵。因此,本研究采用SVD 来实现PCA 运算,以降低PCA 的计算复杂度。快速PCA 运算的主要步骤如下:

步骤1:对数据集X用式(1)进行标准化处理,得到均值为0、标准差为1 的矩阵Xm×n,而Xm×n对应的特征矩阵为Fm×n。

式中,xi为标准化值;x为原始值;xmean为x的平均值;xstd为x的标准差。

步骤2:根据式(2)对Fm×n进行奇异值分解,得到Fm×n的特征向量和特征值矩阵:

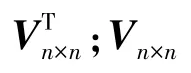
步骤3:利用式(3)将数据集映射到新的特征空间得到旋转后的数据集Xrotate:

2.1.2 PCA 计算次数缩减策略

为提升整个模型的训练速度,使用LightGBM 来训练基分类器。假设最终的RotForest 模型包含L棵树,即RotForest 的集成大小为L,特征集被随机分为Q个特征子集。对于基本的RotForest,需要很长时间来训练这L棵树,因为每生成一棵树,都要对每个特征子集进行PCA 计算,所以整个过程中PCA 共被计算L×Q次。但当使用LightGBM 作为基分类器时,在总计生成L棵树的条件下,将RotForest 和LightGBM的集成大小分别设为S和T(S×T=L)。换言之,一个RotForest 包含S个LightGBM 基分类器,一个LightGBM 基分类器包含T棵树,因此RotGBM 中PCA 总计只执行S×Q次,如此便可在保证分类精度的同时显著提升训练速度。最后通过多数投票策略将各基分类器的预测结果进行整合,得到最终的预测类别。对于一个样本x,其预测标签可通过式(4)得出。

2.2 果蝇优化算法及其改进

果蝇优化算法(FOA)是潘文超于2011年提出的一种群智能进化算法[17]。相比于其他智能优化算法,该算法求解流程简单,可调整参数少,同时具有较快的搜索速度和较低的算法复杂度,已在复杂函数优化、神经网络、SVM 分类器参数优化等领域取得了较好的应用效果[18-20]。但是传统的FOA 算法在收敛速度和求解能力方面还存在一定的不足,并且容易陷入局部收敛。本研究从两个方面对果蝇算法进行改进,提出了一种新的改进果蝇算法(IFOA)。

2.2.1 加入动态调整步长策略

在FOA 算法中,搜索步长R固定为常数,若R设置过小,则收敛速度慢;若R设置过大,则局部寻优能力降低。故本研究通过加入动态调整步长策略,平衡算法的全局搜索与局部搜索能力,主要步长更新公式为

式中,Xaxis和Yaxis是果蝇群体的初始位置;e0为初始权重,设为1.5;a为权重系数,设为0.9;g为当前迭代次数;c为过渡参数;Gmax为最大迭代次数。则R的变化曲线如图2所示。

图2 搜索步长R 的变化曲线Fig.2 Variation curve of search step size R

由图2 可知:随着迭代次数增大,R呈非线性递减趋势变化。在迭代初期,R较大,使果蝇能在全局范围内搜索;在算法后期,R逐步减小,使果蝇能够在某一区域更加精细地搜索。

2.2.2 引入莱维飞行策略

在果蝇搜索过程中,一旦发现最优个体,所有果蝇都会向最优位置靠拢,若该位置只是局部最优而非全局最优位置,则整个种群都会陷入局部最优。莱维飞行是遵循莱维分布的随机搜索方法,可以产生长短不一的搜寻距离,当算法跳入局部区域时,偶尔的长距离可以帮助算法跳出局部最优。故引入莱维飞行策略,在果蝇搜寻过程中增添合理的随机性来保证种群多样性,防止跳入局部最优。主要改进策略如下:

式中,Xbest和Ybest是上一代找到的果蝇最优位置;⊗为点乘;Levy(λ)为遵循Levy分布的搜寻路径且1<λ<3。

一般采用Mantegna 提出的计算公式来求解Levy(λ)[21]:

式中,s为搜索路径Levy(λ);β∈(0,2),一般取β=1.5;参数μ、ν是服从式(10)的正态分布随机数;其相应的标准差取值满足:

2.3 IFOA 优化RotGBM 的故障诊断流程

在上述建立的RotGBM 模型中,由于LightGBM的超参数很多,存在很大的不确定性,影响最终的诊断结果。为了提高整体诊断模型的精度,本研究采用IFOA 对LightGBM 中的5 个重要超参数进行寻优,以得到更为精确的发动机故障诊断模型,超参数的具体信息见表1。

表1 LightGBM 超参数基本信息Table 1 Basic information of LightGBM hyperparameter

IFOA 对LightGBM 进行超参数优化的具体步骤如下:

(1)设置IFOA 算法的基本参数及LightGBM 的超参数范围,并初始化果蝇群体位置。

(2)将发动机故障数据用RF-RFE 算法进行特征提取,然后分为训练集和测试集。

(3)对故障训练集采用LightGBM 模型进行5 折交叉验证,将平均准确率作为适应度函数,计算果蝇个体的适应度值。

(4)降序排列适应度值,取适应度值最大的个体位置为最优个体位置(即当前最优超参数组合),同时记录最佳适应度值。

(5)按照式(5)～式(7)更新果蝇搜索步长R,根据式(8)～式(11)更新果蝇群体位置。

(6)对更新后的果蝇群体计算其适应度值并与最佳适应度值进行比较,从而更新最优个体位置和最佳适应度值。

(7)判断是否满足终止条件,若不满足则返回步骤(4),否则,输出最优超参数组合,寻优结束。

经过上述寻优过程找到最优参数组合后,将其代入RotGBM 模型中,得到最优故障诊断模型对发动机故障训练集进行训练。在故障测试集上进行测试诊断,输出最终的诊断结果。基于IFOA 优化RotGBM的矿用挖掘机发动机故障诊断流程如图3所示。

图3 基于IFOA-RotGBM的矿用挖掘机发动机故障诊断流程Fig.3 Flow of fault diagnosis of mine excavator engine based on IFOA-RotGBM

3 仿真试验与结果分析

为了测试IFOA-RotGBM 诊断模型的性能,本研究借助河南某露天矿潍柴挖掘机的智多星监测装置,采集了潍柴WP13G530E310 发动机的259 组19 维有效故障数据,并在Python3.8 环境中进行多次仿真试验,验证本研究方法应用于矿用挖掘机发动机故障诊断的可行性。

3.1 数据集分布及评估指标

本研究采集了8 种发动机故障类型,分别是正常、高压油泵故障、进气管路堵塞、增压器故障、空滤堵塞故障、风扇故障、中冷器故障、低压油路故障,编号为0～7。从采集的259 组数据中随机抽取59 组作为测试集,其余均作为训练集,并对训练集采用5 倍交叉验证方法进行训练。为避免不同量纲的影响,在训练前对故障数据用式(1)进行标准化处理。训练集和测试集样本数据分布见表2。

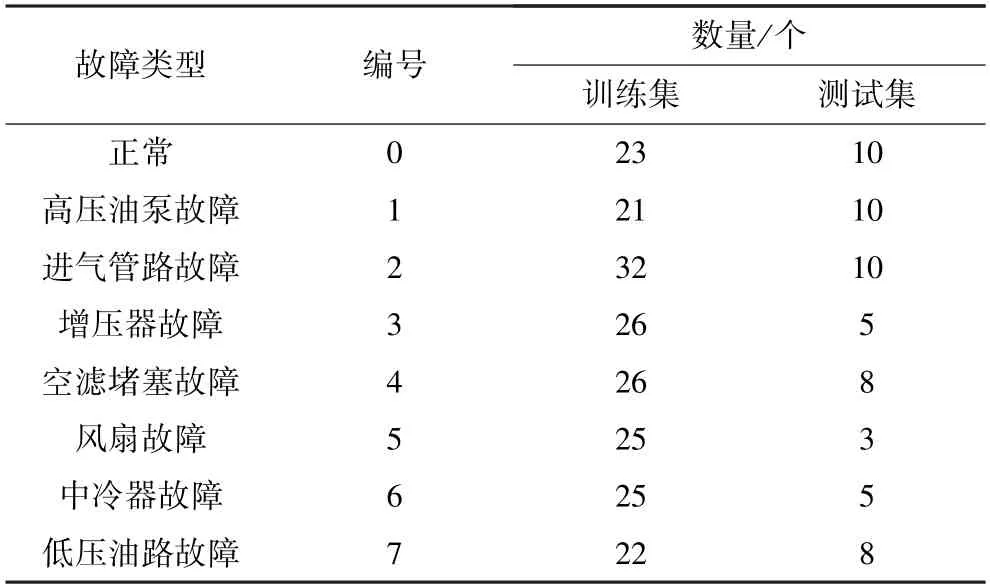
表2 样本数据分布Table 2 Distribution of sample data

一个良好的故障诊断模型不仅要具备更高的诊断精度,还要具有较低的误报率和漏检率。为了全面衡量IFOA-RotGBM 诊断模型的有效性,选取准确率(ACC)、AUC值、误报率(FPR)、漏检率(FNR)和调和均值(F1-Score)作为评估指标。其中,ACC代表诊断精度,AUC值用于检验模型的鲁棒性,FPR和FNR分别表示模型误报和漏报的概率,F1用于综合评估模型的性能。ACC、AUC、F1指标值越高,FPR、FNR指标值越低,表示模型性能越好。上述指标的计算公式为

式中,TP是将故障样本正确预测为故障类别的样本数量;FP是将正常样本错误预测为故障样本的数量;TN是将正常样本正确识别为正常类别的样本数量;FN是将故障样本错误识别为正常样本的数量;Pre为精确率;Rec为召回率。

3.2 特征提取前后算法性能比较

由于采集的发动机故障数据有19 维特征,为了提升模型训练速度,采用RF-RFE 算法对其进行特征提取,选取重要特征子集。故障特征个数和分类精度之间的关系如图4所示。

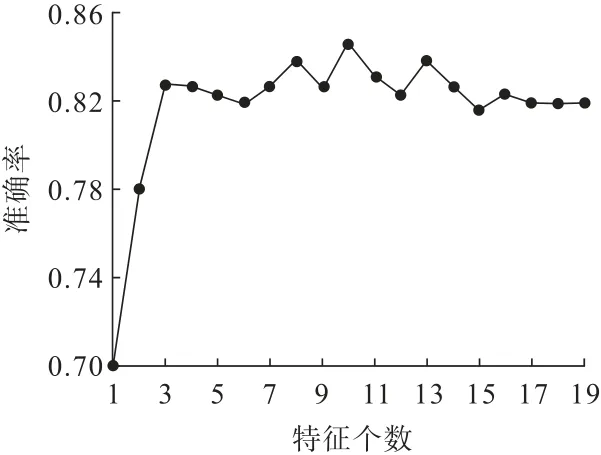
图4 特征个数与准确率的关系Fig.4 Relationship between the number of features and accuracy

由图4 可知:当特征个数为10 时,诊断精度最高,此时相应的由RF 算法计算得到的特征重要性及特征重要性排序见表3。最终选择F2、F3、F7、F9、F11、F12、F14、F15、F18、F19这10 个重要特征组成最终的故障特征集进行挖掘机发动机故障诊断。由于F17同步信号状态特征的重要性为0,故表3 中未列出其特征重要性及排序。

表3 特征重要性排序Table 3 Rank of feature importance

为了进一步分析重要特征提取对于发动机故障诊断效率和精度的影响,对RF-RFE 特征提取前后的训练时间和诊断精度进行了对比分析,结果见表4。由表4 可知:特征维数的缩减可以有效提高故障诊断的效率和精度。

表4 RF-RFE 特征提取前后对比Table 4 Comparison before and after of RF-RFE feature extraction

3.3 不同算法优化LightGBM 的性能比较

为了验证IFOA 对LightGBM 优化的有效性,将训练集进行数据标准化后用IFOA 算法对LinghtGBM进行参数优化。在测试集样本上进行测试,诊断结果与FOA、PSO 和ACO 算法优化LightGBM 的结果进行对比,结果见表5,诊断结果可视化结果如图5所示。

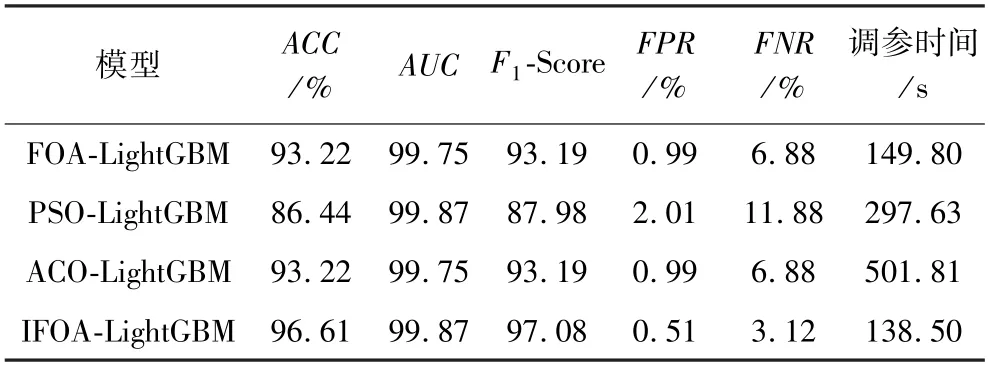
表5 LightGBM 寻优精度结果Table 5 LightGBM optimization precision results

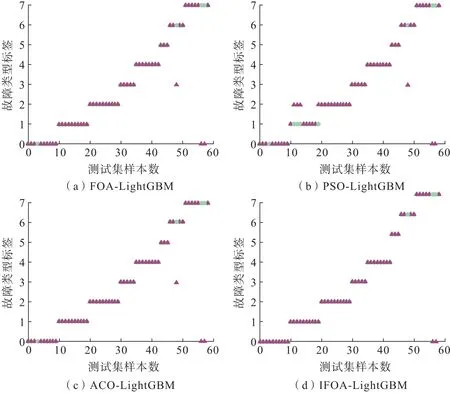
图5 不同算法优化LightGBM 的诊断结果Fig.5 Diagnostic results of LightGBM optimized by different algorithms

由表5 可知:IFOA-LightGBM 模型的整体分类精度最高,具有最低的误报率和漏检率。而且IFOA 对LightGBM 进行调参的运行时间最少,这些都反映出IFOA 优化LightGBM 的优越性。

由图5 可知:PSO-LightGBM 模型对正常状态、高压油路故障、中冷器故障和低压油路故障的识别能力较弱;FOA-LightGBM 和ACO-LightGBM 提高了对高压油路故障的诊断能力,但是对正常、中冷器和低压油路故障的识别率依然较低;IFOA-LightGBM 相较其他3 种方法具有更好的诊断能力,特别是在对正常和中冷器故障的诊断上性能有了明显提升。

3.4 不同故障诊断模型诊断结果分析

为了验证IFOA-RotGBM 故障诊断模型的优越性,本研究选取SVM、BP 神经网络、随机森林、Light-GBM 和旋转森林与其进行诊断性能对比。为确保比较的公平性,对于SVM 和BP 神经网络,参数都设为默认值;对于集成模型来说,基学习器个数是影响模型分类性能的重要因素。对于IFOA-RotGBM 模型,其集成大小为L(L=S×T),其中S设为10,T为需要优化的参数。当IFOA-RotGBM 中T值确定后,4 种集成模型的集成大小均设为L,其余参数设为默认值。每个模型在59 组测试样本上对应于每种故障的识别精度见表6,6 种模型的诊断性能对比见表7。

表6 不同模型对于每种故障的识别精度Table 6 Identification accuracy of different models for each fault%

表7 不同模型诊断精度Table 7 Diagnostic accuracy of different models

由表6 可知:IFOA-RotGBM 相比于其他5 种模型具有最高的平均识别精度,而且其对正常状态、高压油路故障、进气管路故障、增压器故障、空滤堵塞、风扇故障和低压油路故障的诊断能力很强,都能达到100%的故障识别率。特别是对于低压油路故障,其他模型的识别精度只能达到75%和87.5%,而所提模型能达到100%的识别率。

由表7 可知:IFOA-RotGBM 故障诊断模型性能总体上优于其他模型。相比于经典RotForest 模型,预测性能提升了9.4%,而且能达到98.31%的诊断精度、0.22%的误报率和2.5%的漏检率。能够在有限的数据样本条件下获得优异的诊断性能,增强矿用挖掘机发动机诊断模型的容错能力,保证生产正常进行,降低维修成本。