微认证赋能高中生计算思维培养的结构表征与路径设计*

2023-10-19庞敬文马可心王实秋唐烨伟

现代教育技术 2023年10期

庞敬文马可心许晋王实秋唐烨伟

庞敬文1马可心2许晋1王实秋3唐烨伟1

（1．东北师范大学信息科学与技术学院，吉林长春 130117；2．南方科技大学附属坪山学校，广东深圳 518118；3．深圳大学教育学部，广东深圳 518060）

计算思维是高中信息技术学科核心素养之一，但其培养过程中存在教师对计算思维内涵和结构理解浅显、缺少科学理论指导和培养路径混沌等问题，导致学生计算思维能力学力不足、结构零散且评价形式单一。微认证以培养微能力为导向，通过微结构证据划分和认证规范实现个性化评价，其能力导向、结构化和个性化等特征为培养高中生计算思维提供了新思路。因此，文章从微认证视角推演计算思维结构表征和培养路径，首先依据课程将计算思维拆分为四个子能力，以此设计计算思维证据内容和任务类型并形成认证规范；然后文章按照子能力、证据和任务的交互关系，构建呈现能力、要素和路径的计算思维结构；最后文章为计算思维能力提供培养路径案例设计及实施路径，以期为高中信息技术学科计算思维培养提供理论与实践参考。

计算思维；微认证；结构表征；路径设计；高中信息技术

当前，《普通高中信息技术课程标准（2017年版2020年修订）》（下文简称《标准》）已将计算思维列入高中信息技术学科核心素养[1]，并作为关键要素对信息技术课程育人目标的达成度起重要作用。而计算思维的抽象性本质使教师对其概念缺乏系统性理解，对其教学缺乏科学性实践，导致计算思维培养路径并不明晰[2]。目前，国内有关高中生计算思维培养的研究多是依据特定工具或内容所展开的教学模型、模式与活动设计类的探索，存在应用场景有限、适应性较差等问题，且无法为教师提供计算思维培养导向的教学路径底层设计思路。而微认证是我国学者探索出的关于计算思维评价的全新视角，在该视角下可将K12阶段学生的计算思维分解为六个子能力，并分别设计评价方式[3]。虽然有关计算思维与微认证相结合的研究处于初步探索阶段且仅限于评价领域，但两者的适切性为计算思维的培养提供了新的视角和思路。为此，本研究尝试基于微认证推演计算思维的培养与发展过程，实现对高中生计算思维的结构表征与培养路径设计的深入探究，以期为高中信息技术学科计算思维培养提供理论与实践参考。

一核心概念阐述

1 计算思维与计算思维培养

当前，国内外对计算思维内涵的理解尚未达成一致。其中，国外学者普遍从拆解角度探究计算思维内涵，即分析构成要素或构建整体框架，具有代表性的是计算思维发展与评估三维框架：计算概念、计算实践和计算观念[4]，以及从计算思维过程视角归纳的五要素：算法思维、分解、抽象、概括和评价[5]。2015年，ISTE构建了由创造力、算法思维、批判性思维、解决问题、合作思维和沟通技巧构成的计算思维框架[6]。以上观点与微认证理念对计算思维的理解相统一，均将其划分为细小的能力或要素单位，甚至组织为一个结构框架。国内学者对计算思维内涵的理解存在不同，但都认为其是意识、方法和能力等的综合反映，具有程序化、自动化和模块化等特点。分歧点在于其本质取向，可划分为工具说、问题解决说、活动和方法说等观点[7]。其中，问题解决说观点占据主流，如任友群等[8]认为计算思维是一种解决问题的过程，借助计算思维学生可以更好地理解问题和分析问题并形成问题解决方案。而《标准》中将计算思维界定为运用计算机科学领域思想方法形成问题解决方案过程中产生的一系列思维活动。基于此，融合微认证视角，本研究将高中生计算思维界定为运用计算机解决问题的方式进行思考、分析、应用与实践的综合性能力，包括分析问题、抽象特征、设计算法和总结迁移等多项能力。

2 微认证的概念特征、运作体系与认证规范

（1）微认证概念及特征分析

微认证的出现是为了解决教师非正式学习所获能力缺少正规评估方式的问题，美国教育研究协会呼吁转变学习结果评估形式，为便于学习成果展示和分享，发展出数字徽章标记学生所掌握的能力[9]。2014年，微认证开始用于评估和认定教师能力。国内学者研究了微认证内涵与运作体系，明确了包含认证机构、内容和证据等要素的认证体系[10]，用于教师能力评估。微认证实现了更加开放、个性化的能力评价，特点是：①细化能力要求，将复杂能力分解为多个子能力，便于观察和测量；②清晰界定子能力，有助于收集和记录学习过程，丰富考核内容促进培养方式多元化；③留出弹性空间满足学生的个性化需求。由此，应用微认证赋能高中生计算思维培养，可促进计算思维导向教学路径设计，提升高中生计算思维培养质量。

（2）微认证运作体系和认证规范

微认证是多要素协作完成的系统性评价工作，各要素间的角色分配及交互关系需高质量运作体系的界定和支持。美国对微认证的应用模式和推进策略等展开研究，研究内容可总结为认证目的、项目、流程、结构分析与结果调查五部分[11]。在国内，闫寒冰等[12]阐述了我国开放学习微认证运作体系，认为体系和获得徽章的方法是促进学生成长的关键因素。魏非等[13]构建包括角色分析、能力分解、规范开发和调研试用四个阶段的开发过程模型，设计包括35项微能力的微认证规范框架和体系，并依据《标准》拆分能力，为微认证开发提供参考和实施路径。基于此，本研究以证据为中心，遵循能力-证据-任务的设计逻辑，拆分计算思维子能力并设计认证规范。

二微认证赋能高中生计算思维结构表征

证据是对能力最直接的评价与证明，而任务包括能够产生并提供证据的情境、任务特征和内容等。因此，本研究在规范设计时以证据为中心，首先依据计算思维子能力划分证据类型，将其作为连结能力与任务的桥梁；然后根据证据类型设计相应的任务集合，明确彼此间的对应关系；最后将能力、证据和任务三者依据彼此间的关系结合，设计高中生计算思维的认证规范。

1 计算思维能力拆分

（1）计算思维子能力维度划分

《标准》对计算思维能力的描述可概括为解决问题前的分析类能力、解决问题时的设计类能力以及解决问题后的迁移类能力。而思维三棱结构理论认为，思维是一个由目的、过程、品质、材料、自我监控和非认知因素构成的多侧面、多形态和多联系结构，六要素相互协作并共同完成一次思维活动[14]。因此，将《标准》中的能力描述与思维结构要素相对应，可得到四项微能力：分析问题目标能力、设计问题解决过程能力、材料处理能力和自我监控能力。同时，将思维三棱结构理论中两个未对应的要素重新聚类。思维结构中的品质要素表示计算思维能力发展水平，如学生解决问题过程中表现出的创新性、灵活性等。《标准》也强调要划分计算思维发展水平，因此将不同的品质要求在不同的发展水平中区分描述。思维结构中的非认知因素表示解决问题过程中产生影响的态度和习惯等，可根据教学实践将其概括为“对解决问题产生影响的个人因素”，包括正向和非正向影响。基于非认知因素中的个性化差异，在计算思维结构中不对此能力单向表征，而是在设计路径时与结构中的任务和证据一同体现。

（2）计算思维子能力水平划分

微认证要求拆分子能力要具体、详细、可观测，用合格与优秀划分完成情况。基于此，本研究采用《标准》中核心素养发展的发展级、进阶级和拔尖级（预备级是学生高中前就应具备的能力和基础，不作为培养的目标水平）三个层级来描述高中生计算思维发展水平，具体如表1所示。

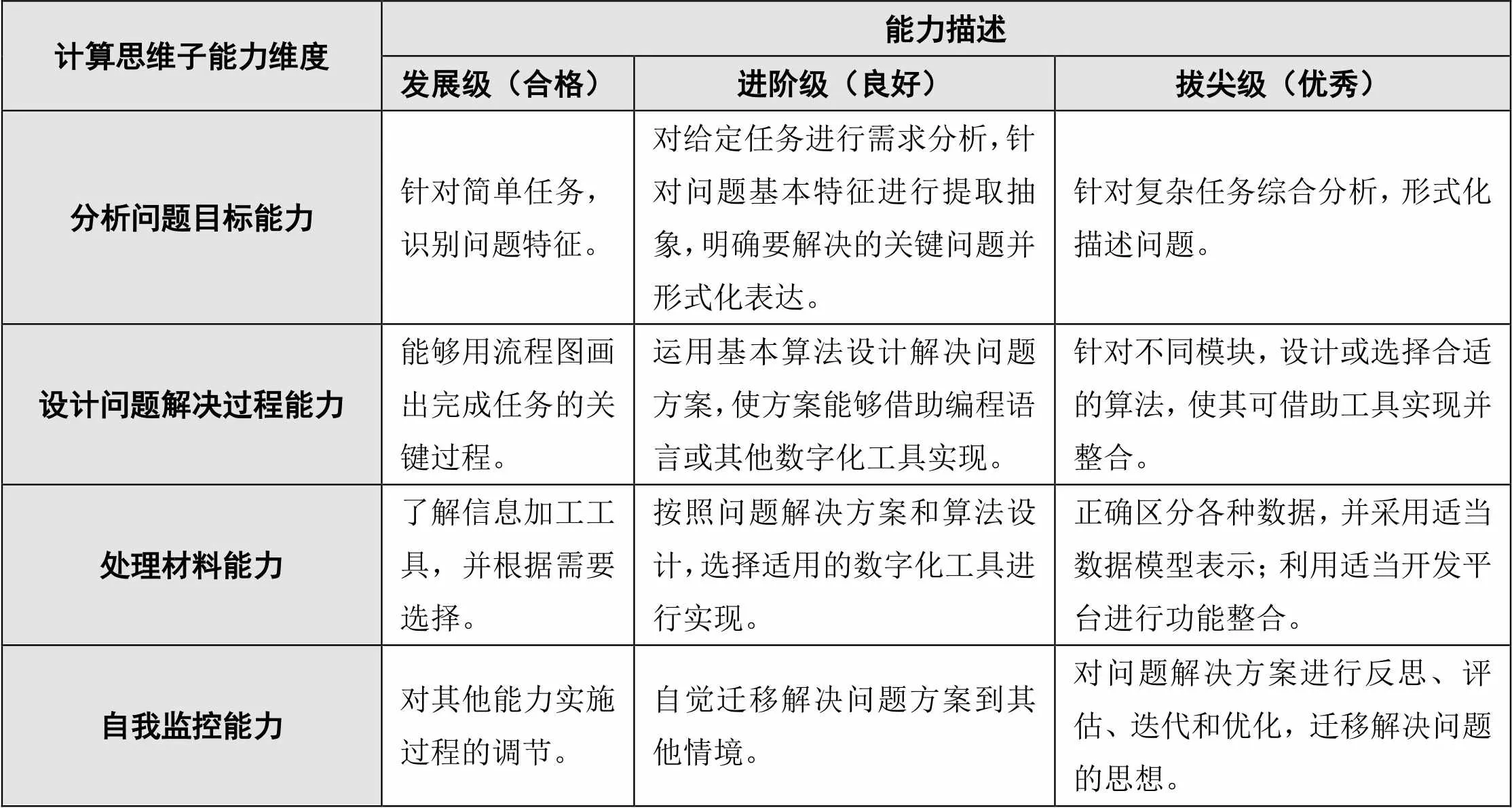
表1 高中生计算思维子能力及其发展水平描述

2 计算思维认证规范设计

（1）证据类型划分

证据是学生能力发展的行为映射，对行为的评估方式一般包括直接观察和作品检验，本研究采取作品检验方式围绕作品划分证据类型。而评价的证据与评价方式相关，为防止对计算思维的理解产生偏差，一般采用多元评价方式，需为计算思维各子能力选择对应的评价方式并据此划分证据类型。研究者按不同的分类方式划分计算思维评价工具和评价方法；评价工具方面，分类方式较多，如范文翔等[15]按照评价途径将思维评价工具分为总结性、技能转移性、迭代性以及看法与态度量表等；评价方法方面，主要包括总结性评价、过程性评价、形成性评价等。

本研究采用总结性评价和形成性评价，通过图示分析和图文分析丰富高中生计算思维各子能力的评价方式，并依据子能力评价方式划分微认证所需的证据类型，具体如表2所示。

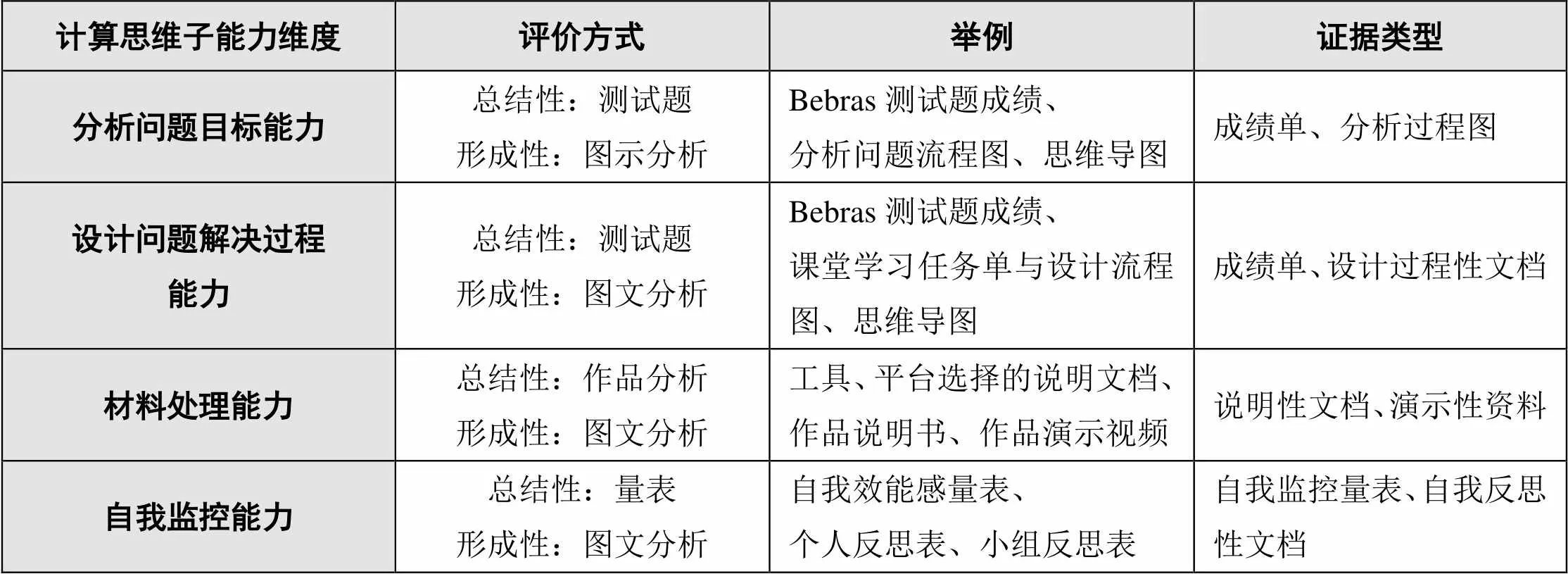
表2 高中生计算思维评价方式

（2）任务集合归类

任务指能够通过特定设计产生评价证据并使其可被采集的实践活动，任务设计要关注证据，并为其产生提供活动基础。《标准》中对培养学生计算思维能力的活动按照解决问题过程概括为前期分析与组织、中期选择与设计和后期评价与迁移三个任务维度。本研究基于已有任务类型和对高中生计算思维子能力的分析，总结了计算思维的四种任务类型，并说明其与子能力及证据类型的对应关系，所有任务共同构成计算思维的任务集合。

①分析理解型任务：包括对问题、信息和情境等多元要素的接收、理解、处理和分析。证据为学生的分析过程图，对应评价的子能力为分析问题目标能力。②设计创新型任务：包括针对目标借助已有材料解决方案的设计、整合、创新与优化等任务。证据包括设计过程性文档，如思维导图、流程图、任务单和设计框架等过程性资料，对应评价的子能力为设计问题解决过程能力。③筛选实践型任务：包括对解决问题过程中遇到的所有材料进行筛选并付诸实践。证据为作品的说明性文档、演示性资料以及材料选择的对比分析说明，对应评价的子能力为材料处理能力。④反思提升型任务：包括应用计算思维解决问题过程中的评价与反思及迁移和自我提升。证据为学生自我监控量表与自我反思性文档，对应评价的子能力为自我监控能力。

（3）认证规范设计

接下来，依据以上证据类型与任务设计，设计认证规范，并结合能力特点设计数字徽章。其中，数字徽章显示子能力维度、发展水平和学生姓名三项信息，同时携带的元数据包含学生完成的任务、提交的证据材料及教师评语等内容。用T、P、M、S表示目标、过程、材料和自我监控四个子能力，用数字1、2、3代表发展级、进阶级和拔尖级三个水平，用A、B表示证据和任务，如AT1表示认证“分析问题目标能力”达到发展级所需的证据，具体如表3所示。

3 计算思维结构表征

基于上述计算思维子能力拆分和证据类型与任务集合设计，本研究在微认证视角下将三者与思维结构中的非认知因素构建为一个整体，更加清晰地反映高中生计算思维结构，为其培养路径提供参考，同时在表征中针对非认知因素和不同的发展水平为教师教学保留弹性空间，以满足个性化需求，具体如图1所示。

借鉴思维三棱结构将计算思维构建为一个三棱锥，并划分为三个层级，图1中最底部的粗线条表示发展级，依次向上两种细线条分别表示进阶级和拔尖级，三个三棱锥共同构成计算思维三棱三级结构。结构中顶点、边/棱、面的具体含义如下：

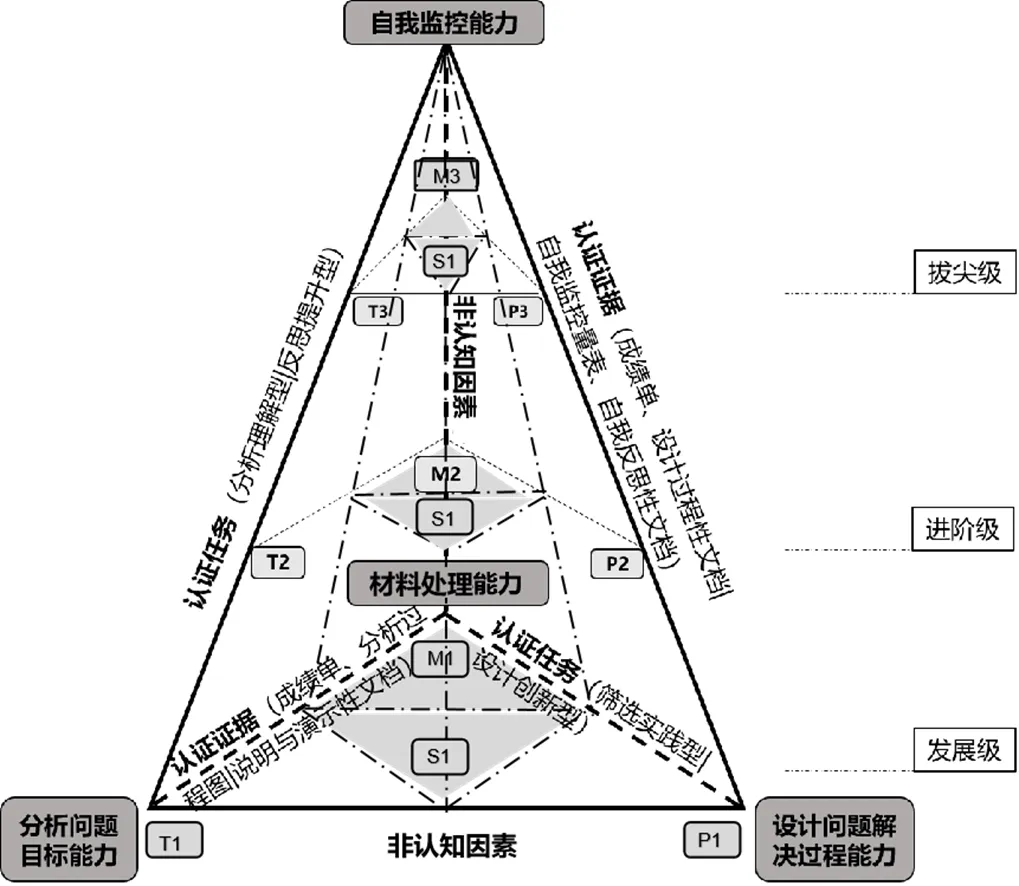
图1 高中生计算思维结构表征图

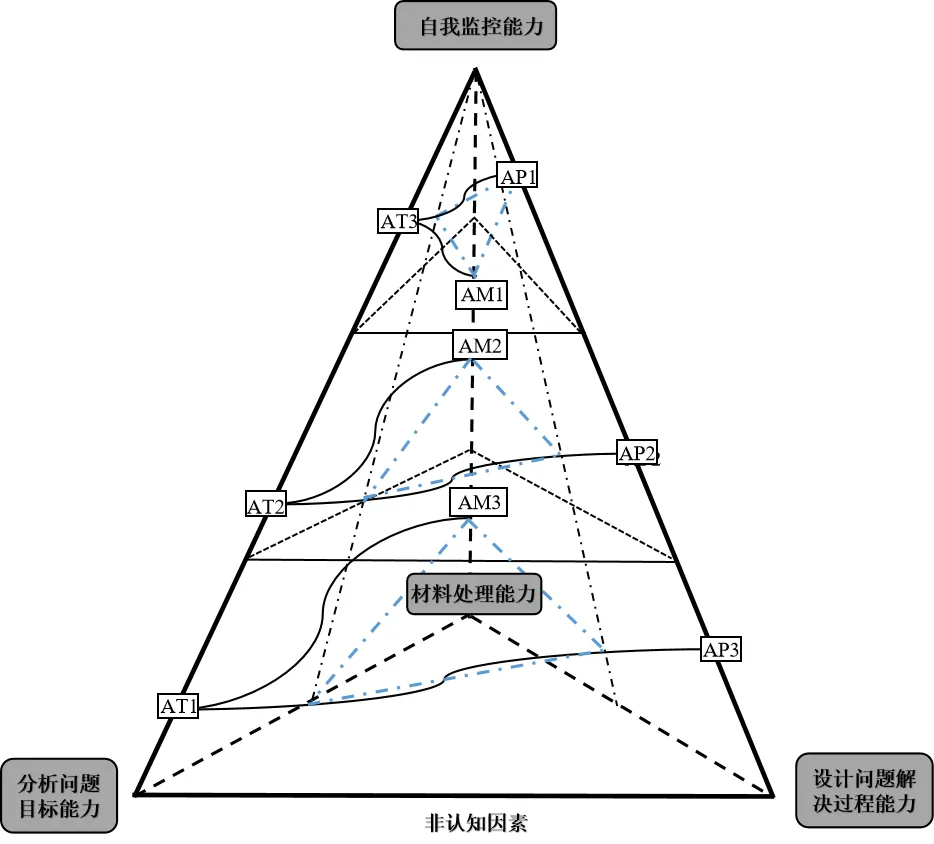
图2 高中生计算思维培养路径结构图

①顶点。计算思维三棱三级结构根据计算思维的三个发展水平划分为三个三棱锥，每个三棱锥的四个顶点分别代表计算思维的四个子能力，在图中用带方框的文字表示，其中有关计算思维目标、过程、材料三个维度的子能力分别位于每个三棱锥的底面三角形顶点。由于自我监控是对其他子能力进行监控和调节的能力，因此三棱锥的重合顶点表示自我监控能力在每个层面都发挥作用，影响整个计算思维水平提升的过程。同时，自我监控能力具有较强的个体差异性，不同学生的表现不尽相同。

②边/棱。每个三棱锥均包含三个底边和三条侧棱，从每个能力顶点出发有三条棱，代表任务、证据和非认知因素，表示在培养该子能力时要综合考虑相邻三条边所包含的内容，即分析培养该子能力需提供的认证证据、产生此类证据的任务类型。设计相应教学任务还要考虑产生影响的非认知因素，如学生情感、习惯和性格等，共同促进子能力的发展。基于此，一个三棱锥中的每条边服务于两个子能力顶点，六条边共被拆分为两个证据、任务和非认知因素的组合，每两条名称相同的边所包含的证据或任务内容因其相邻的两个子能力顶点变化而变化，而不同三棱锥中同样的位置代表不同发展水平的边所蕴含的证据和任务会随着水平变化而有所不同。

③面。每个三棱锥共有四个面，每个面是由含义不重复的三条边构成的三角形，在培养计算思维子能力时，会途经由该子能力顶点出发的三条不同的边，每两条边连接形成了计算思维培养路径，因此计算思维三棱结构的面呈现出差异化的培养路径。同时，图中阴影部分代表的面是自我监控能力所在边的顶点向分析问题目标能力、设计问题解决过程能力、材料处理能力所在边做中线，并将中线所在的点与非认知因素所在的点相连而形成的平面区域，表示非认知因素对学生发展级、进阶级、拔尖级三个层级每一层级的影响。图中的阴影是最理想的状态，即非认知因素对每一个等级、每一项能力都产生相同的影响。在实际的教学中，产生影响的非认知因素所在的区域每一个顶点，根据实际情况可以是四个能力所在边的任一点。

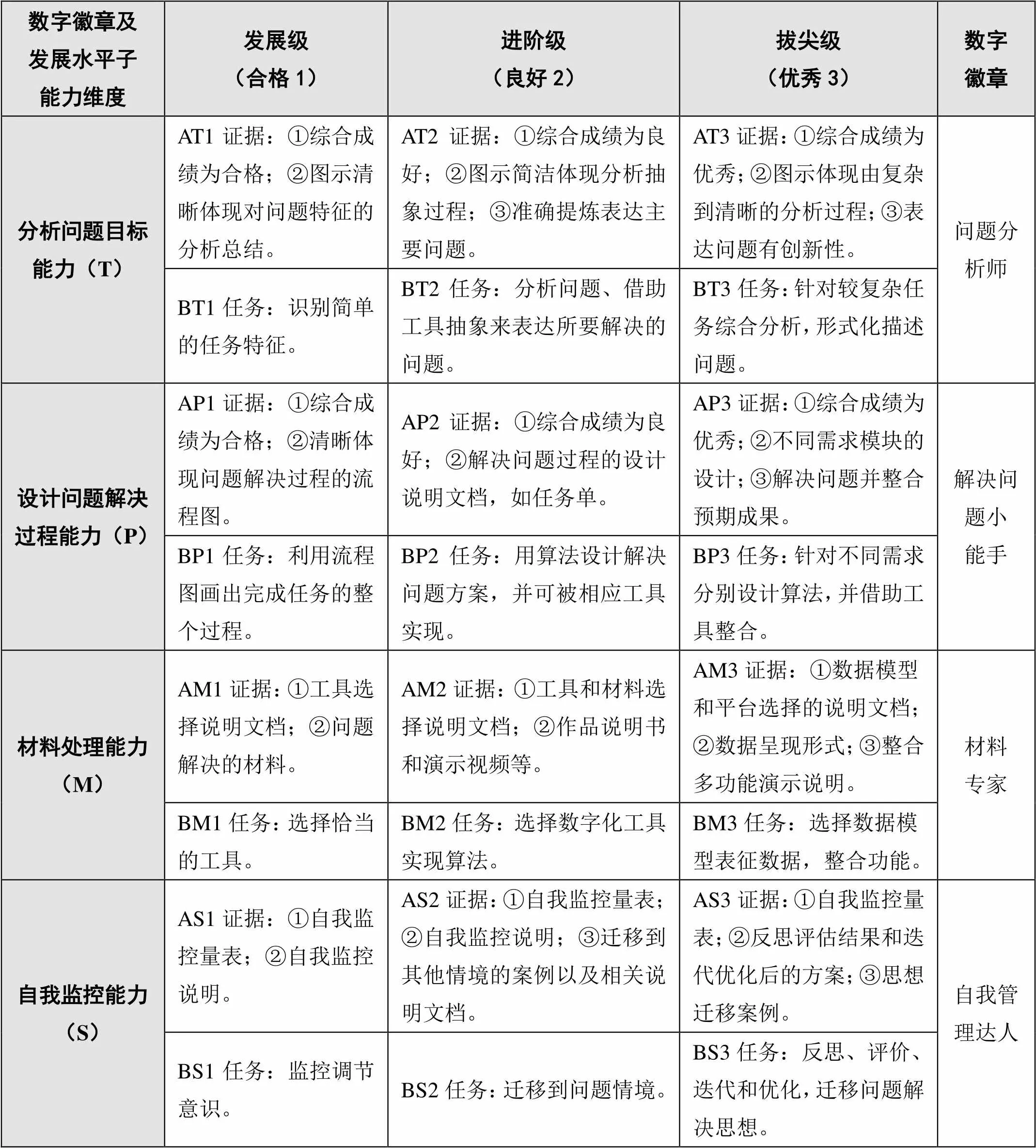
表3 认证规范

三基于高中生计算思维结构的培养路径设计

高中生计算思维三棱三级结构为高中生计算思维的培养策略研究提供了新的思路。本研究根据该结构提出计算思维培养的总体路径为：①依据认证规范确定计算思维子能力对应的证据内容；②依据证据内容确定能够提供该证据的任务类型；③结合学生的非认知因素设计相应的教学任务，进而培养该计算思维子能力。本研究使用表3认证规范中相应的字母组合统一表达，用C表示结构中的非认知因素，C与子能力的字母、数字组合则表示在培养该水平子能力时教师应考虑的可能会对任务完成、证据产生和其他学习活动产生影响的相关因素。由于非认知因素具有较强的个体化差异，因此教师可根据学生情况精准地培养其计算思维子能力。基于以上总体路径和组合含义，可对各子能力设计具体的培养路径，不同水平的培养路径在计算思维三棱三级结构中所处层级不同但方向一致。另外，高中生各计算思维子能力发展水平不一定处于同一层级，表明不同水平的三个三棱锥之间并不彼此独立，因此培养计算思维时各子能力之间的路径可跨越不同层级的任务和证据，构成高中生计算思维培养路径结构图，如图2所示。

1 分析问题目标能力教学路径

培养高中生分析问题目标能力的教学路径可以表示为AT1→AT2→AT3。根据子能力选定代表成绩单和分析过程图的证据AT1，由此出发选定相应的分析理解型任务（BT1、CT1、DT1……）；完成任务BT1后再根据AT2证据选择相应的任务（BT2、CT2、DT2……），以此类推。最后，根据教学内容和学生特点分析并矫正对该子能力产生影响的非认知因素ST，如设计融合非认知因素发展的德育活动并提升学生兴趣，最终路径将呈现在三棱锥中分析问题目标能力所在三角形的三条边与三个顶点T1、T2、T3构成的两个侧面上。

2 设计问题解决过程能力教学路径

培养高中生设计解决问题过程能力的教学路径可以表示为AP1→AP2→AP3。依托于代表该子能力的顶点P1及其相邻的三条边。根据子能力选定代表成绩单和分析过程图的证据AP1，由此出发选定相应的分析理解型任务（BP1、CP1、DP1……）；在完成任务BP1的基础上，再根据AP2证据选择相应的任务（BP2、CP2、DP2……），以此类推。最后，根据教学内容和学生特点分析并矫正对该子能力产生影响的非认知因素SP，如引导学生养成设计解决问题解决过程的思维习惯，最终路径将呈现在三棱锥中设计问题解决过程能力所在三角形的三条边与顶点P1、P2、P3构成的底面和侧面上。

3 材料处理能力教学路径

培养高中生材料处理能力的教学路径可以表示为AM1→AM2→AM3。依托于代表该子能力的顶点M1及其相邻的三条边。根据子能力选定代表成绩单和分析过程图的证据AM1，由此出发选定相应的分析理解型任务（BM1、CM1、DM1……）；在完成任务BM1的基础上，再根据AM2证据选择相应的任务（BM2、CM2、DM2……），以此类推。最后，根据教学内容和学生特点分析并矫正对该子能力产生影响的非认知因素SM，如设计融合非认知因素发展的其他学科核心素养内容，最终路径将呈现在三棱锥中材料处理能力所在三角形的三条边与顶点M1构成的底面和侧面上。

4 自我监控能力教学路径

培养高中生的自我监控能力，要在非认知因素所在范围内，将发展级、进阶级、拔尖级三个等级中其他三项能力所处的顶点与相应等级的非认知因素相连，由此组成的区域为非认知因素对学生学习的影响范围，范围越大，表示非认知因素对学生的能力提升影响越大。教师可以清晰地看到每一项能力的非认知因素对学生能力产生的影响，并据此调整教学。

四基于高中生计算思维结构的培养路径案例设计及实施路径

1 案例设计

（1）教学材料

本研究以教育科学出版社《信息技术基础》的第二章第四节“网络数据库的信息检索”为例，具体分析高中生计算思维结构的培养路径。该章节的目标是使学生学会利用网络数据库查找和获取专业性强、主题明确的信息资源，共三小节：体验-使用-评价。

（2）教学活动

教学活动的基本过程如表4所示，这里创设的情境为全校“网络法律知识竞赛”。

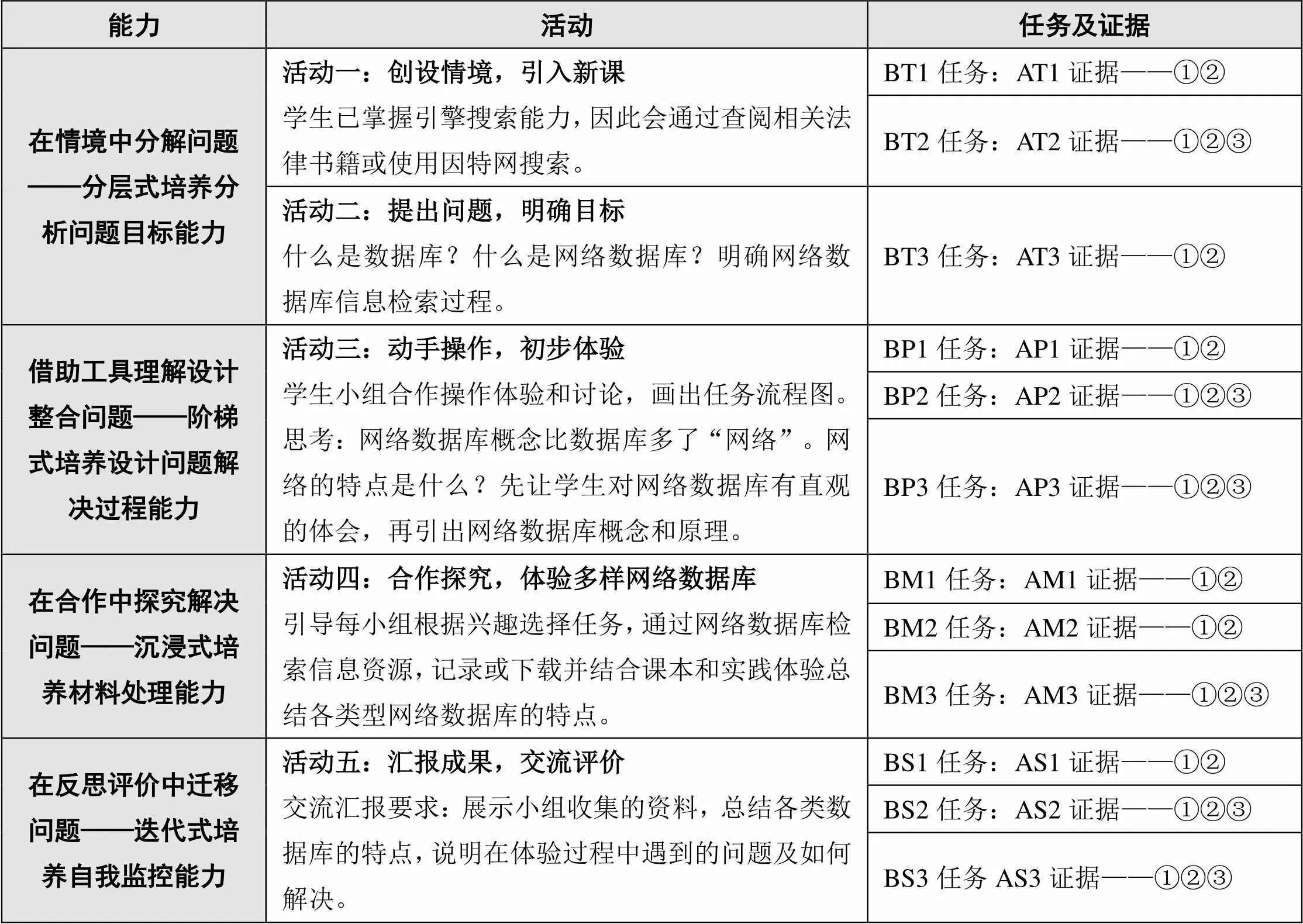
表4 教学活动的基本过程

2 实施路径

（1）在情境中分解问题——分层式培养分析问题目标能力

计算思维能力可帮助学生更好地理解和运用信息技术，提高其分析、设计、创新和解决问题等能力。在教学中，应从培养学生的分析问题目标能力入手，这样一方面可帮助学生更好地理解目标，另一方面可培养学生对信息的表达和传递能力。因此，教师可首先结合学生已知知识为其创设基于实际经验的问题情境，使其针对简单任务，识别问题特征。同时，引导学生结合已有知识尝试思考解决问题所需的技术和方法，在学生分析得到可用的解决方法后，教师适时启发其尝试寻找新的未知方法以更高效、便捷地完成问题解答，形成多种路径解决问题的思维模式。然后，教师依据教学目标将问题分解成可察觉、可把握的子问题，引导学生对给定任务进行需求分析、借助工具对问题进行分析和描述，针对问题的基本特征提取抽象，明确要解决的关键问题并形式化表达。最后，教师明确问题，帮助学生形成对问题的完整思路图，针对较为复杂的任务进行综合分析，并形式化描述问题。同时，教师需要为学生创设情境，与学生合作，并通过引导学生分析问题和目标进而引入要讲授的新课，教师不直接提出问题，而是将问题分解，让学生在问题和目标的分析过程中识别问题；在学生经过思维碰撞形成由模糊到清晰的过程后，教师进一步帮助学生明确目标，使其在充分理解问题和目标的基础上，利用工具最终确定要解决的问题、关键问题并对这些问题进行描述，实现分层式逐级培养学生的分析问题目标能力。

（2）借助工具理解设计整合问题——阶梯式培养设计问题解决过程能力

高中信息技术学科中计算思维培养最核心的部分，是在充分理解算法的基础上应用其实现问题求解和问题解决。而算法是一个抽象的概念，因此对问题解决过程的设计尤为重要，一方面学生在设计问题解决过程时可从宏观全局角度理解和分析问题；另一方面，学生要进行归纳和分析，进而抽象出问题的共性和本质，形成抽象模型，以实现将计算机图形界面转化为相应的算法。因此，在教学中教师可首先引导学生通过横向对比、纵向延伸等将问题系统整合，对相应概念及特点进行讲解，帮助学生明晰问题解决的关键步骤和关键过程，并通过图示化的方式将其可视化表达，呈现解决的具体过程。然后，教师让学生列举具体实例，帮助其巩固对问题中概念和原理的理解，并在此基础上针对问题进行深入思考，通过概念的对比、分析，引起对问题中关键要素的注意，以此促使学生运用基本算法设计解决问题方案，使方案能够借助编程语言或其他数字化工具实现。最后，教师针对问题和相应算法设计不同需求的算法方案，使学生在反复的实践中体会和理解相应的概念和原理，以及应用算法解决问题的一般过程，在此过程中教师需要通过直观的方式，帮助学生理解较抽象的问题，进而实现教学重难点突破，在学生的实际操作中阶梯式分层培养学生的设计问题解决过程能力。

（3）在合作中探究解决问题——沉浸式培养材料处理能力

高中信息技术学科中的计算思维培养离不开学生对各种数字化工具、算法设计等的理解和合理化应用与选择，因此在学习过程中需要不断培养学生处理材料的能力，这样一方面可以帮助学生更好地运用计算机软件和硬件进行信息处理、传输和分析；另一方面有利于学生提高自身的认知水平进而反向促进其问题解决能力。在教学中，教师可首先组织学生合作学习以共同商讨并了解信息加工工具，体验不同工具的实际特点和应用场景，在探究中根据问题解决的需要进行选择。然后，教师针对不同需求设计应用场景和案例，学生小组内选择场景共同探究，制订问题方案、设计问题解决路径，按照问题解决方案和算法选择适用的数字化工具展开合作交流、探究。为满足学生个性化发展的条件，问题的解决方案和路径一定是多选择、多线条的。最后，对于收集的大量数据，教师要引导学生通过合作探究实现多维度、多流向的数据区分，择优用以建立相应数据模型，并在教师引导下利用合适的开发平台对其整合。在此过程中，教师为学生不断地创设真实场景和环境，在沉浸式体验中培养学生的材料处理能力。

（4）在反思评价中迁移问题——迭代式培养自我监控能力

计算思维培养需要学生随时调控其自我监控能力，在学习和问题解决过程中调动情感态度以支持其更好地进入学习环境和学习状态。对学生自我监控能力的培养，一方面有利于学生在信息技术课程中较好地保持学习积极性和专注度，另一方面对学生的整个学习过程乃至生命全过程起着至关重要的调节和监控作用。因此，在教学中教师可首先引导学生反思（包括自我反思、小组反思等），并在个人或小组学习后，组织学生汇报交流，使其了解自我学习过程和学习状态并自我监控，为学生创设更多对自我其他能力实施过程进行调节的机会，增强其监控调节意识。然后，教师需为学生制定评价的规则和标准，引导其在自学、合作、探究学习中评价自我和他人，特别是问题解决过程中要提醒学生做好记录，在评价中汇总问题和方案，自觉将解决问题方案迁移到其他情境中。最后，教师需引导学生系统性迁移，将反思结果和评价结果相结合进行交叉分析，引导学生从情境出发，对问题解决方案再反思、再评估，寻找优化方案，将问题解决的思想迁移，使其在反思、评价、迁移的过程中不断迭代式优化自我监控能力。

五结语

本研究意在从微认证视角表征高中生计算思维结构，以实现对高中生计算思维各项能力的提升和强化，但计算思维内涵丰富且结构复杂、难以精准评估、子能力分散又相互关联，因此在培养路径设计中并没有提供具体的实施建议。为此，本研究首先以计算思维为导向的信息技术教学需要教师在宏观上整体把握教学方向、明确育人目标，加强对计算思维内涵的深层次、多维度理解；其次，教师应全面分析学情，并据此明确计算思维任务和证据类型，可结合计算思维挑战赛试题，协同评估判断；最后，计算思维各子能力并非完全独立且毫无关联，每个子能力对应的教学任务互相衔接可共同组成一系列主题任务，在实际教学中，教师可设计不同子能力融合培养的主题项目，主题下各任务互相衔接，实现主题项目中不同子能力的综合培养。

[1]教育部.教育部关于印发普通高中课程方案和语文等学科课程标准(2017年版2020年修订)的通知[OL].

[2]张进宝.计算思维教育:概念演变与面临的挑战[J].现代远程教育研究,2019,(6):89-101.

[3]魏非,祝智庭.微认证:能力为本的教师开放发展新路向[J].开放教育研究,2017,(3):71-79.

[4]Brennan K, Resnick M. New frameworks for studying and assessing the development of computational thinking[OL].

[5]牟琴,谭良,周雄峻.基于计算思维的任务驱动式教学模式的研究[J].现代教育技术,2011,(6):44-49.

[6]孙立会,王晓倩.计算思维培养阶段划分与教授策略探讨——基于皮亚杰认知发展阶段论[J].中国电化教育,2020,(3):32-41.

[7]Wing J M. Computational thinking[J]. Communication of the ACM, 2006,(3):33-35.

[8]任友群,隋丰蔚,李锋.数字土著何以可能?——也谈计算思维进入中小学信息技术教育的必要性和可能性[J].中国电化教育,2016,(1):2-8.

[9]杨盼,曲中林.美国教师微认证述评[J].上海教育科研,2019,(4):31-36.

[10]Berland M, Wilensky U. Comparing virtual and physical robotics environments for supporting complex systems and computational thinking[J]. Journal of Science Education & Technology, 2015,(5):628-647.

[11]Korkmaz O, Cakir R, Ozden M Y. A validity and reliability study of the computational inking scales (CTS)[J]. Computers in Human Behavior, 2017,72:558-569.

[12]汪维富,闫寒冰.面向开放学习成果的微认证:概念理解与运作体系[J].电化教育研究,2020,(1):60-68.

[13]魏非,闫寒冰,祝智庭.基于微认证的教师信息技术应用能力发展生态系统构建研究[J].电化教育研究,2017,(12):92-98.

[14]郁晓华,肖敏,王美玲.计算思维培养进行时:在K-12阶段的实践方法与评价[J].远程教育杂志,2018,(2):18-28.

[15]范文翔,张一春,李艺.国内外计算思维研究与发展综述[J].远程教育杂志,2018,(2):3-17.

Research on Structural Characterization and Path Design of Computational Thinking Training for Senior High School Students Empowered by Micro-certification

PANG Jing-wen1MA Ke-xin2XU Jin1WANG Shi-qiu3TANG Ye-wei1

Computational thinking is one of the core literacy of information technology discipline in senior high schools, but there are some problems in its training, such as teachers’ simple understanding on the connotation and structure of computational thinking, lack of scientific theory guidance and chaos of the training path, etc., which lead to students’ insufficient learning ability of computational thinking, scattered structure and single evaluation form. Oriented to the cultivation of micro-ability, micro-certification realized personalized evaluation through the division of micro-structure evidence and certification specification, and provided a new way to cultivate senior high school students’ computational thinking with its features of ability orientation, structuration and personalization. Therefore, this paper deduced the structure representation and cultivation path of computational thinking from the micro-authentication perspective. Firstly, computational thinking was divided into four sub-abilities according to the curriculum, and the computational thinking evidence content and the task types were designed, and the certification specification was formed. Then, on the basis of the interactive relationship of sub-ability, evidence and task, a computational thinking structure that presented ability, elements and path was constructed. Finally, the paper provided a case design and implementation path for the training of computational thinking ability, in order to provide theoretical and practical reference for the training of computational thinking in senior high school information technology discipline.

computational thinking; micro-certification; structural characterization; path design; senior high school information technology