复合工况下平顺性优化体系的建立及仿真验证

高 洁，陈 克

复合工况下平顺性优化体系的建立及仿真验证

高 洁1，陈 克2

（1.大连交通技师学院（大连市交通口岸职业技术学校）轨道交通系，辽宁 大连 116013； 2.沈阳理工大学 汽车与交通学院，辽宁 沈阳 110159）

平顺性优化是提升车辆性能的重要途径。文章基于正交试验设计，建立复合工况下平顺性优化体系。选择平顺性综合评价值和悬架参数作为优化目标和优化变量，确定约束条件和因素水平，编制试验方案。采用仿真试验研究法，完成复合工况下的平顺性试验，分析悬架参数不同因素水平对平顺性影响的主次关系。研究结果表明，复合工况能综合考虑路况条件和车速影响，反映车辆真实行驶状态，悬架参数的最优组合使整车平顺性得到综合提升，验证了平顺性优化体系的合理性和可行性。

平顺性；正交试验设计；综合评价；仿真试验研究法；复合工况

提升驾乘舒适度[1]、改善车辆平顺性是在研车型设计和旧款车型升级改造的关键。在影响平顺性的诸多因素中，悬架作为重要的传力连接装置，对提升平顺性影响直接、操作可行、效果明显。在反映真实行车状态的复合工况下，选择科学的优化方法，建立合理的优化体系，分析车辆悬架系统的最佳参数匹配条件，对改善汽车平顺性有重要的实际意义。

复合工况下的汽车平顺性优化体系是采用试验设计方法[2-4]，依据正交试验设计思路[5-7]，构建一个目标变量明确、参数条件限定、方案执行合理的优化程序[8-9]，用以解决不同路面工况、不同车速条件、不同测量点等复合试验工况下平顺性的优化问题，确保优化的系统性、全面性和可靠性。

本课题将依据正交试验设计理论，首先，建立复合试验工况下平顺性优化体系，选择平顺性综合评价值和悬架弹簧刚度曲线值、减振器阻尼曲线值作为优化目标和优化变量，确定5个相关的约束条件，并以±10%和±20%浮动已设定的优化变量值，确定4个因素水平，选择16(45)正交表，编制16组试验方案，通过对获取的试验数据进行计算处理，分析悬架系统中不同因素对平顺性的影响程度，得出研究车辆在复合试验工况下行驶时，悬架系统各性能参数的最优组合情况。接着，在指定复合工况下完成平顺性仿真试验，通过数据对比，验证平顺性优化体系的合理性和可行性。

1 平顺性非线性仿真试验系统

1.1 整车仿真模型

以某型运动型多功能车（Sports Utility Vehicle, SUV）为研究对象，基本参数如表1所示。

联合HyperMesh、ANAS、PreSys/VPG等虚拟仿真技术，建立整车非线性仿真模型，如图1所示。整车装配后，经统计，整车仿真模型共有538 135个节点，540 720个单元模块，其中梁单元32个，壳单元527 149个，实体单元13 308个，质量单元231个。经测算，模型总质量为1 620.3 kg，前轴载荷46%，后轴载荷54%，该数据与实车参数相匹配，符合仿真试验条件。

表1 车辆基本参数

参数参数值参数参数值 整备质量/kg1 620轴距/mm2 660 排量/L2.4前轮距/mm1 560 长(mm)×宽(mm)×高(mm)4 630×1 855×1 720后轮距/mm1 560 前悬架类型麦弗逊式独立轮胎规格225/65 R17 后悬架类型双叉臂式独立径向刚度/(N/mm)325 前悬架轴荷/kg854径向阻尼比0.05 后悬架轴荷/kg680静摩擦系数0.94 前悬架刚度/(N/mm)31动摩擦系数0.74 后悬架刚度/(N/mm)30胎压/kPa220

图1 整车仿真模型

1.2 复合路面仿真模型

为反映车辆真实行驶状态，让研究车辆以不同车速通过不同路面，具体仿真试验工况如表2所示。

首先，基于HyperMesh的二次开发，读取和编辑B级随机路面和脉冲路面的高程数据，分别创建随机平直路面、随机弯曲路面、脉冲路面几何模型。接着，在PreSys中调整三个路面的位置，并将相邻的重叠节点捏合，使三个路面共享边界节点，完成复合路面仿真模型的建立。最后，通过ANSA软件的网格检查和修复功能，检查路面单元法向，如有问题，需通过修复功能转换单元法向。

表2 试验工况

路面工况随机平直路面随机弯曲路面脉冲路面 路长/m503010 试验车速/(km/h)604020

1.3 仿真试验系统

经整车仿真模型的建立，相关连接和各部分接触的定义以及计算条件的设定后，最终建立平顺性仿真试验系统，如图2所示。

图2 仿真试验系统

参照《汽车平顺性试验方法》（GB/T 4970－2009）[10]进行仿真试验，定义模型计算初始步长1.0e−6 s，终止时间8.6 s，计算机每执行5 000次循环后记录一次数据。采用计算机辅助工程（Com- puter Aided Engineering, CAE）云计算方式，通过提交仿真模型K文件进行计算，获取驾驶员座椅面、驾驶员座椅靠背和驾驶员脚部地板面三个测试点在时域和频域下的仿真试验数据，并计算平顺性综合评价指标，对研究车辆的平顺性做出评价分析。

2 复合工况下平顺性优化体系的建立

应用正交试验设计理论，建立复合工况下平顺性优化体系，主要步骤如下：

1.选择平顺性优化目标

依据平顺性评价标准以及多层次模糊综合评价体系[11-12]的内容，选择车辆平顺性综合评价值作为优化目标：

式中，z为车辆平顺性综合评价值，是在平顺性综合评价模糊评价集基础上，建立研究车辆在不同试验工况和车内不同测试点位置的平顺性能值关系矩阵，通过考虑不同测试点位置，完成一级模糊评价，再通过考虑不同试验路况，完成二级模糊评价，获得的平顺性综合评价值。

2.选择平顺性优化变量

对现有车型平顺性进行优化时，由于相关元件的选择和安装已完成，车辆主要部件结构的修改受功能、成本、工艺等因素的限制。因此，本课题选择对悬架弹簧刚度和减振器阻尼的非线性曲线值进行调整，以实现对研究车辆整车平顺性能的优化提升，同时，也可为新车型的参数设计提供可靠的试验数据和合理的分析结论。平顺性优化变量：

式中，f、r分别为前后悬架弹簧刚度参数，N/mm；f、r分别为前后悬架减振器阻尼参数，N·s/mm。

3.确定平顺性优化约束条件

为保证在车辆结构参数优化时不影响车辆其他性能，在进行优化时要对悬架进行基本的约束，具体内容如下：

1）悬架对称约束

考虑到悬架设计时左右具有对称性，在仿真试验分析时，对车辆进行了简化，设置悬架左右结构和参数相同，即

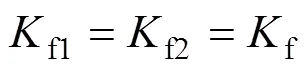
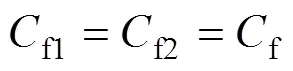
2）悬架刚度约束

要获得车辆良好的平顺性，就要尽量降低悬架刚度，而悬架刚度的降低会导致车身固有频率的降低，这就要求悬架有较大的静挠度。此外，为尽量减少车身纵向角振动，这就要求后悬架的静挠度要比前悬架的静挠度小一些。已知研究车辆悬架静挠度的设计范围为100～300 mm，则悬架刚度约束：

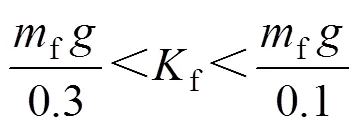
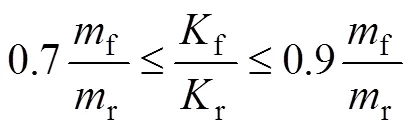
式中，f、r分别为前、后悬簧载质量，kg。

3）悬架阻尼约束

在车辆悬架减振器阻尼的设计中，振动衰减的快慢程度要用相对阻尼系数体现。已知研究车辆悬架减振器相对阻尼系数的取值范围为0.25～0.35，则悬架阻尼约束为

4）悬架动挠度约束

受悬架结构的约束，悬架动行程[d]的取值范围为70～90 mm。为了保证悬架动行程在行驶时撞击限位块的概率小于0.3%，则悬架动挠度均方根值约束为

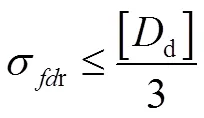
式中，[d]为悬架动行程，mm；σdf、σdr分别为前、后悬架动挠度均方根值。

5）悬架偏频约束

考虑前后悬架合理的共振频率，悬架偏频约束为

式中，f、r分别为前、后悬架偏频。

4.确定平顺性优化因素水平

依据所选择的平顺性优化变量，确定悬架弹簧刚度和减振器阻尼4个因素水平，每个因素以初始值±10%和±20%浮动，建立试验设计分析的因素水平，如表3所示。

表3 平顺性试验设计分析因素水平表

水平因素前悬架弹簧刚度后悬架弹簧刚度前悬架减振器阻尼后悬架减振器阻尼 水平1-20%-20%-20%-20% 水平2-10%-10%-10%-10% 水平3+10%+10%+10%+10% 水平4+20%+20%+20%+20%

获得悬架弹簧刚度和减振器阻尼的非线性曲线值变化情况，如图3－图6所示。

5.选择适合平顺性优化的正交表

选用四水平标准正交表16(45)[2]，代表因素水平数4个，因素数5个，平顺性优化试验次数为16次，正交表的具体内容参照前文所述的因素水平变化情况。

图3 前悬架弹簧刚度水平变化情况

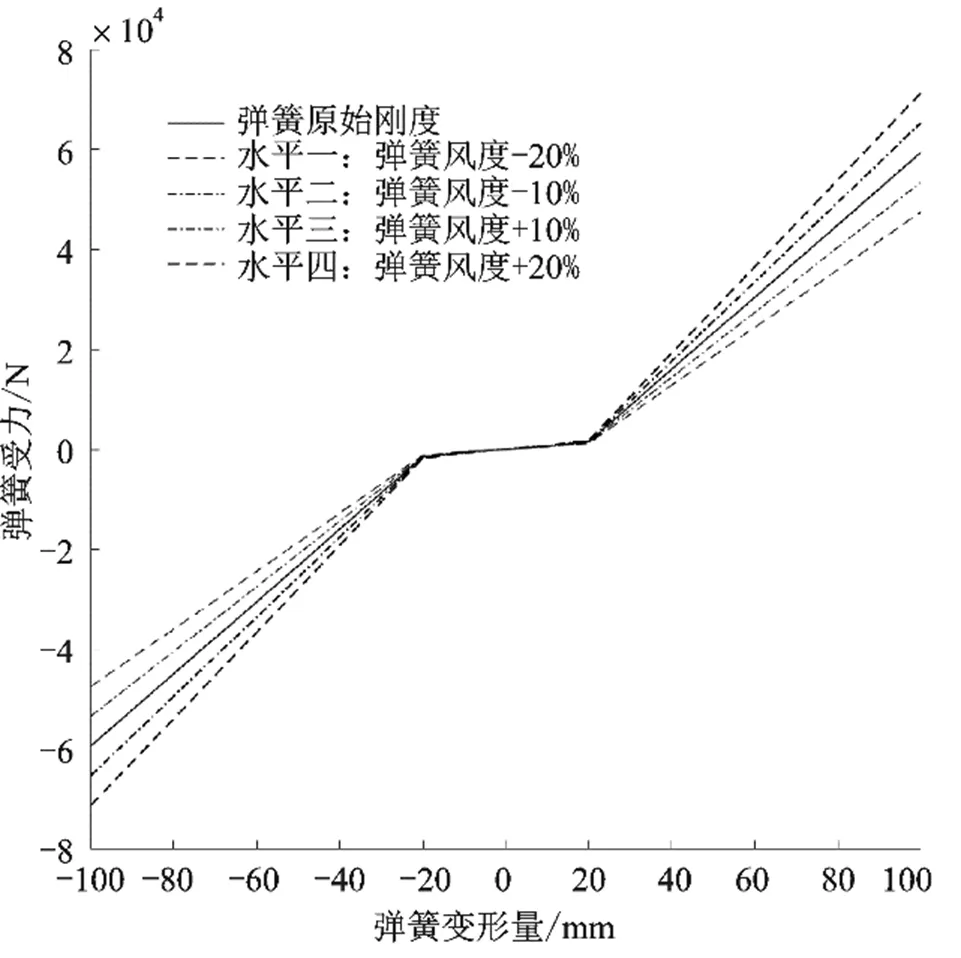
图4 后悬架弹簧刚度水平变化情况

图5 前悬架减振器阻尼水平变化情况

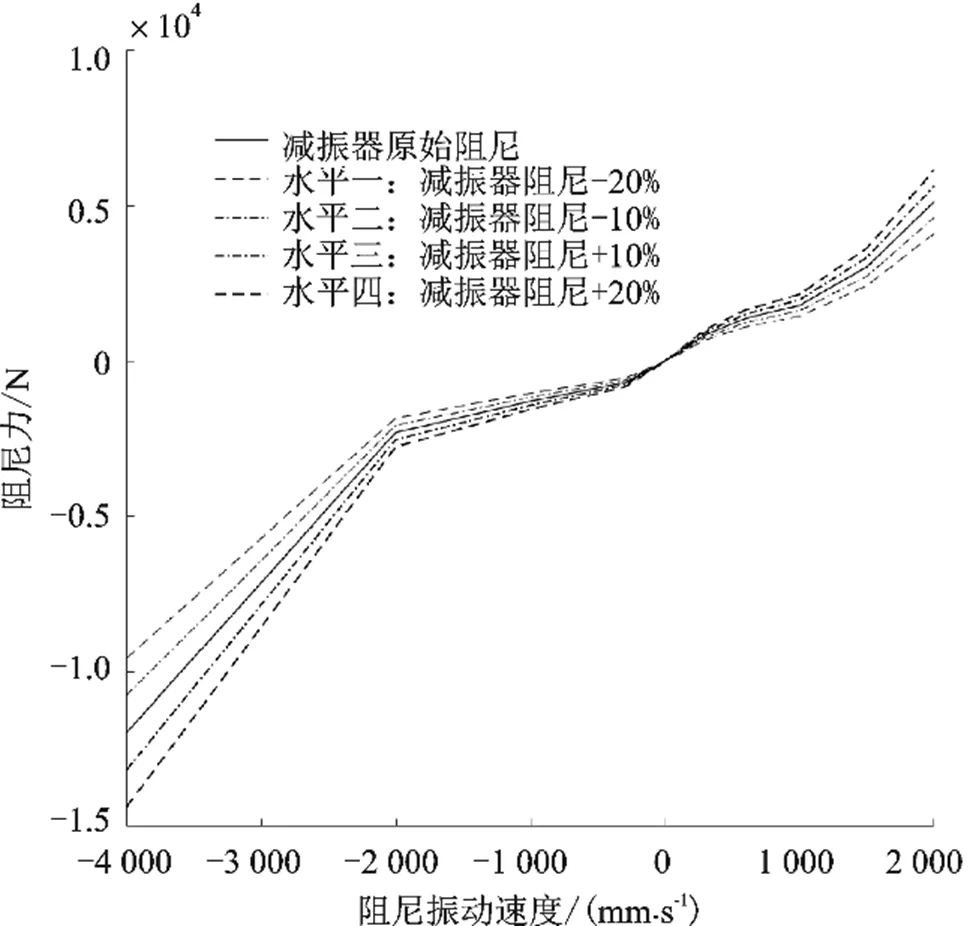
图6 后悬架减振器阻尼水平变化情况

6.编制平顺性优化仿真试验方案及获取试验结果

按照正交表编制平顺性优化仿真试验方案，在平顺性仿真试验系统中完成试验，并获取试验结果，如表4所示。

表4 平顺性优化仿真试验方案

试验因素 前悬架弹簧刚度后悬架弹簧刚度前悬架减振器阻尼后悬架减振器阻尼空列平顺性综合评价值 试验1111110.937 2 试验2122220.937 6 试验3133330.935 9 试验4144440.931 9 试验5212340.943 6 试验6221430.935 7 试验7234120.928 3 试验8243210.923 5 试验9313420.941 2 试验10324310.936 5 试验11331240.913 5 试验12342130.908 5 试验13414230.935 9 试验14423140.925 6 试验15432410.918 7 试验16441320.910 9

7.分析平顺性优化仿真试验结果

首先，分析各因素对指标影响的主次。

式中，K为试验方案中第列因素水平所对应的试验指标之和；为因素数。

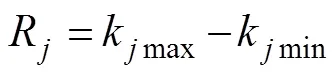
式中，R为第列因素的极差，反映的是第列因素水平波动时，试验指标的变动幅度；R越大，说明该因素对平顺性的影响越大。

接着，确定各因素应采取的水平。因素水平的选取与要求的指标有关，对于汽车平顺性研究，要求平顺性综合评价值越大越好，代表驾乘人员舒适性越好，因此，本课题应选取值对应指标最大的水平。

最后，确定各因素应采取水平的最佳组合。充分考虑影响平顺性的主次因素情况，按照有利于指标的要求选取水平，确定各因素的最佳组合方式。

经计算，得到平顺性优化直观分析表，如表5所示。

表5 平顺性优化直观分析表

指标因素 前悬架弹簧刚度后悬架弹簧刚度前悬架减振器阻尼后悬架减振器阻尼 K13.742 63.757 93.697 33.699 6 K23.731 13.735 43.708 43.710 5 K33.699 73.696 43.726 23.726 9 K43.691 13.674 83.732 63.727 5 k10.935 70.939 50.924 30.924 9 k20.932 80.933 90.927 10.927 6 k30.924 90.924 10.931 60.931 7 k40.922 80.918 70.933 20.931 9 R0.012 90.020 80.008 90.007 0 主次因素Kr＞Kf＞Cf＞Cr 最优方案Kf1Kr1 Cf4Cr4 最优方案水平-20%-20%+20%+20%

表5中的数据表明，影响研究车辆平顺性能的主要因素依次是后悬架弹簧刚度、前悬架弹簧刚度、前悬架减振器阻尼和后悬架减振器阻尼。研究车辆平顺性优化的最佳组合方式是前悬架刚度曲线值-20%，后悬架刚度曲线值-20%，前悬架减振器阻尼曲线值+20%和后悬架减振器阻尼曲线值+20%。

3 复合工况下平顺性优化体系仿真验证

依据国标平顺性评价方法[10]，计算研究车辆各测试点的振动综合加权加速度均方根值和振动计量值，并对比优化前后的数据[13]，如表6所示。

表6 优化前后研究车辆各测试点数据对比

试验工况测试点位置座椅面(m/s2)座椅靠背(m/s2)地板面(m/s2)XYZXYZXYZ 优化前随机平直路面，车速60 km/h0.186 30.183 00.201 90.473 30.465 60.530 10.454 80.454 50.488 0 0.3300.4930.253 随机弯曲路面，车速40 km/h0.278 90.272 80.304 40.621 10.600 20.634 80.728 80.765 40.824 7 0.4950.6340.423 脉冲路面，车速20 km/h1.150 01.149 41.570 53.193 53.194 54.233 63.100 33.098 04.113 7 2.2613.4561.977 优化后随机平直路面，车速60 km/h0.169 90.166 80.187 90.437 00.429 30.497 10.419 20.418 90.457 5 0.3030.4560.236 随机弯曲路面，车速40 km/h0.263 00.257 10.286 50.609 30.591 70.607 90.708 90.737 90.787 3 0.4660.6200.406 脉冲路面，车速20 km/h1.271 01.270 41.701 33.528 63.529 54.623 13.405 73.403 44.454 5 2.4753.8082.150

表6中的数据表明，优化后，车辆在随机路面行驶时，研究车辆各测试点各轴向的加权加速度均方根值和总加权加速度均方根值都有不同程度的减小，而在经过脉冲路面时，却出现了比较明显的增大情况。这说明，复合工况下，车辆结构参数的优化对平顺性优化呈现不同的影响效果，车辆在某一段路况下平顺性的提升不能代表全路况下平顺性能的优化情况，还可能制约、降低车辆在其他路况连续行驶时的平顺性能。因此，为确保车辆平顺性优化的合理性，需综合考虑车辆实际的行驶工况。

再依据平顺性综合评价体系，计算得到研究车辆优化前后，各测试点的平顺性综合评价值，优化前后的数据对比，如图7所示。

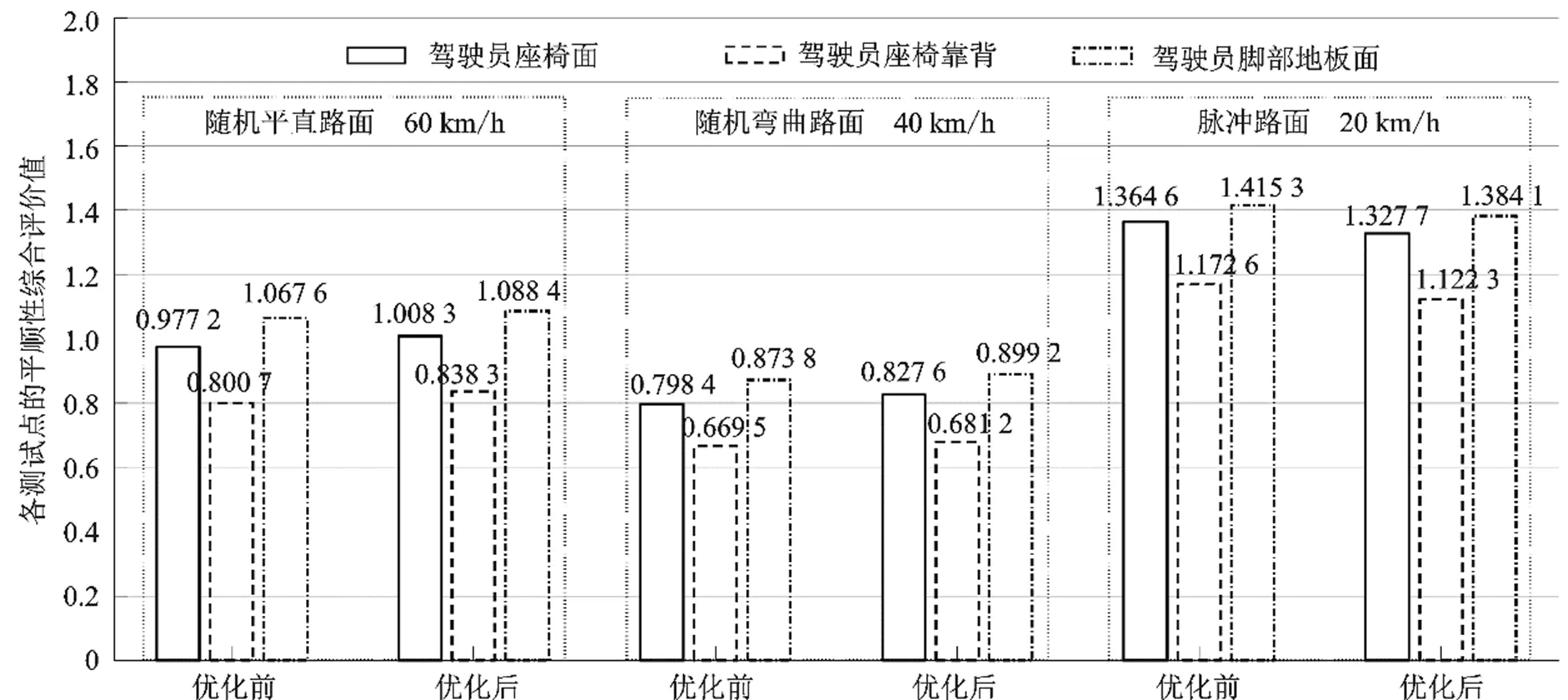
图7 优化前后研究车辆各测试点的平顺性综合评价值对比

同时，对比车辆优化前后的平顺性综合情况，如表7所示。

表7 优化前后研究车辆平顺性综合情况对比

对比内容模型优化前模型优化后优化情况 综合评价值0.933 90.952 9提升 2.03% 人的主观感觉有一些不舒服有一些不舒服略有改善 评价等级二级（好）二级（好）保持不变

4 结论

本课题基于正交试验设计理论，建立了复合试验工况下平顺性优化体系，并确定5个相关的约束条件和4个因素水平，选择16(45)正交表，编制试验方案。依据所需复合试验工况，完成整车平顺性仿真试验，通过对比优化前后相同试验条件下的数据，得出如下主要结论：

1）车辆悬架参数优化后，各测试点在随机平直路面行驶的平顺性综合评价值平均提升了3.3%，在随机弯曲路面行驶的平顺性综合评价值平均提升了2.5%，在脉冲路面行驶的平顺性综合评价值平均降低了3.1%，整体平顺性综合评价值提升了2.03%，虽然评价等级保持不变，但驾乘人员感觉略有改善。

2）本次研究车辆平顺性优化的最佳组合方式对随机振动输入的减振效果较好，却不能很好的应对突发较大的脉冲输入。由于随机路面在复合路况中占比最大，所以随机路面下车辆平顺性的提升对整车平顺性综合优化起到积极的作用，验证了在复合试验工况下进行车辆平顺性优化，方法可行、结果可靠。

[1] 张文春.汽车理论[M].北京:机械工业出版社,2005.

[2] 任露泉.试验设计及其优化[M].北京:科学出版社, 2009.

[3] ALDAIR A, ALSAEDEE E, ABDALLA T. Design of ABCF Control Scheme for Full Vehicle Nonlinear Active Suspension System with Passenger Seat[J]. Iranian Journal of Science and Technolog,Transac- tions of Electrical Engineering,2019,43(1):289-302.

[4] OUAIDAT G, CHEROUAT A, KOUTA R,et al. Sensi- tivity Analysis of the Uncertainties of the Mechanical Design Parameters: Stochastic Study Performed Via a Numerical Design of Experiment[J].International Journal of Hydrogen Energy,2021,27(46):14659-14673.

[5] MING W W,LONG C,XIU J Z,et al.Numerical Sim- ulation of Stamping Forming for an Automobile Rein- forced Plate Based on Orthogonal Test[J].Advanced Materials Research,2013,602(12):1988-1902.

[6] BIRHANU B,SHEWIT W,GOYTOM D.Multi Stage and Multi Response Process Optimization in Taguchi Method[J].Zede Journal,2015(33):88-93.

[7] 李晶,郭小汝,徐阳,等.基于Moldflow和Taguchi正交试验的汽车空调外壳安装板注射成形工艺参数优化[J].兰州工业学院学报,2016,23(3):76-78.

[8] UYS P,ELS P,THORESSON M.Suspension Settings for Optimal Ride Comfort of Off-road Vehicles Travelling on Roads with Different Roughness and Speeds[J].Journal of Terramechanics,2007,44(2):163- 175.

[9] YONG J L,SHA H L,CUI Y W.Orthogonal Test Opti- mization of Vehicle Smoothness and Road Friendlin- ess[J].International Journal of Applied Mathematics & Statistics,2013,21(51):592-600.

[10] 中国国家标准化管理委员会.汽车平顺性试验方法: GB/T 4970－2009[S].北京:中国标准出版社,2009.

[11] 卢兆麟,李升波,周吉晨.结合自然语言处理与改进层次分析法的乘用车驾驶舒适性评价[J].清华大学学报(自然科学版),2016(2):137-143.

[12] 潘伟.车辆乘坐舒适性评价方法研究[D].镇江:江苏大学,2017.

[13] 高洁,张军.多工况随机输入下的某SUV平顺性试验研究及其性能分析[J].机械设计与制造,2021(1):179- 184.

Establishment and Simulation Verification of Ride Comfort Optimization System under Composite Working Conditions

GAO Jie1, CHEN Ke2

( 1.Rail Transit Department, Dalian Technician College of Transportation ( Dalian Traffic and Port Vocational School ), Dalian 116013, China; 2.College of Automobile and Transportation, Shenyang Ligong University, Shenyang 110159, China )

Ride comfort optimization is an important aspect to improve vehicle performance. The ride comfort optimization system under composite working conditions is established based on the orthogonal experimental design in this paper. The comprehensive evaluation value of ride comfort, suspension parameters are selected as the optimization objectives and variables, the constraint conditions and factor levels are determined, and the test scheme is formulated. The simulation test research method is used to complete the ride comfort test under composite working conditions, and the primary and secondary relationship of different factors of suspension parameters on ride comfort are analyzed. The test results show that the composite working conditions can reflect the real driving state of the vehicle by considering the influence of road conditions and speed comprehensively. The optimal combination of suspension parameters can comprehensively improve vehicle ride comfort performance, the rationality and feasibility of the ride comfort optimization system are verified.

Ride comfort; Orthogonal experimental design; Comprehensive evaluation; Simulation test researchmethod; Composite working conditions

U462

A

1671-7988(2023)19-116-07

10.16638/j.cnki.1671-7988.2023.019.023

高洁（1984－），女，博士，高级讲师，研究方向为汽车动力学仿真，E-mail:gaojie_1314@126.com。