基于跃度信号的自动驾驶横向控制

李沐恒，罗奕永，王 祥，程 翔

基于跃度信号的自动驾驶横向控制

李沐恒，罗奕永，王 祥，程 翔

（广州汽车集团股份有限公司 汽车工程研究院，广东 广州 511434）

针对自动驾驶车辆的横向控制，提出了一种基于跃度信号的预瞄控制。建立车辆二自由度动力学误差模型，采用线性二次调节（LQR）反馈控制和前馈控制构成闭环横向控制模型。以CarSim和Simulink为仿真平台，模拟车辆进入并跟踪稳态圆。通过分析横向位置误差和横摆角误差等指标，表明该预瞄算法在横向控制精度、跟踪速度方面具有良好效果。

自动驾驶汽车；预瞄控制；路径跟踪；横向控制；二自由度车辆模型

自动驾驶功能可以有效降低驾驶员的驾驶负荷，提高公路利用率，解决交通拥堵问题[1]。自动驾驶功能可以大体分解为感知、决策、控制三大部分[2]。

在横向控制中，以横向位置误差、横摆角误差作为评价指标。实现横向算法的控制方式主要有比例-积分-微分（Proportion Integral Differential, PID）、线性二次调节器（Linaer Quadratic Regulator, LQR）和模型预测控制（Model Predictive Control, MPC）等方法。PID技术使用时间长、研究广泛、相对成熟，但作为无模型控制器，PID参数需要通过大量测试进行调校以达到预期效果[3]。MPC和LQR都属于最优控制，以状态方程和物理环境为边界条件，通过求解在约束下的系统性能泛函实现最优控制。MPC控制精度高，但由于计算量较大，需要运算能力较强的处理器单元。线性二次调节器运算量较少，且可以通过离线计算提前得到各个条件所对应的控制量，在控制过程中直接调用结果，能够保证控制的时效性[4]，所以目前在工程中主要以PID和LQR控制为主。

本文采用静态前馈和LQR反馈的联合控制，以车辆二自由度动力学误差模型为被控对象，以跃度信号为预瞄模型的控制输入，对状态信息进行提前调整，解决物理系统存在的滞后性问题。最后通过联合仿真验证了该跟踪算法的有效性。

1 系统误差模型建立

1.1 二自由度动力学模型

相比于车辆运动学模型，动力学模型中考虑轮胎侧偏特性，以力平衡和力矩平衡作为等式基础，可以更准确地描述车辆横向状态。图1为前轮转向车辆的二自由度动力学模型。其中，为整车质心；为运动瞬心；Ff为前轴侧向力；Fr为后轴侧向力；f为前轮侧偏角；r为后轮侧偏角；f为前轴速度；r为后轴速度；为质心速度；为横摆角；f为质心到前轴的距离；r为质心到后轴的距离；为轴距；为质心侧偏角；为前轮转角。设前轮转角较小，对应质心侧偏角也较小。根据力学关系可得力平衡和力矩平衡关系式。

图1 车辆二自由度动力学模型

车辆横向受力平衡公式[5]：

ma=Ff+Fr（1）

车辆横摆力矩平衡公式：

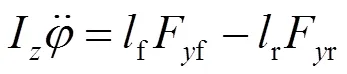
考虑轮胎侧偏特性在线性区，可得

Ff=Cff（3）

Fr=Crα（4）

式中，为整车质量；a为侧向加速度；Cf为两个前轮侧偏刚度之和；Cr为两个后轮侧偏刚度之和；I为过车辆质心绕轴的转动惯量。

对前、后轴做速度分解，可得

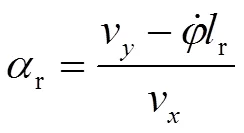
整理式（1）－式（6），可得动力学微分方程的矩阵表达形式：

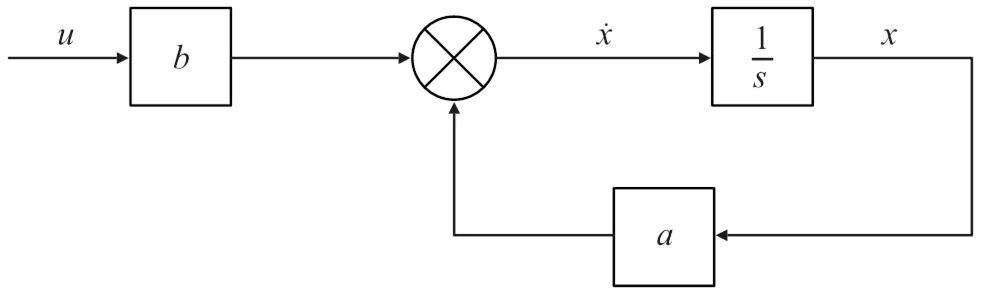
图2 动力学模型框图

1.2 系统误差模型

将动力学方程的坐标变换至Frenet坐标系，并用n表示横向位置误差，表示航向角误差，=-r。其中，r为路径航向角。将状态变量的阶数从1阶扩展至0阶，整理动力学方程的误差方程为

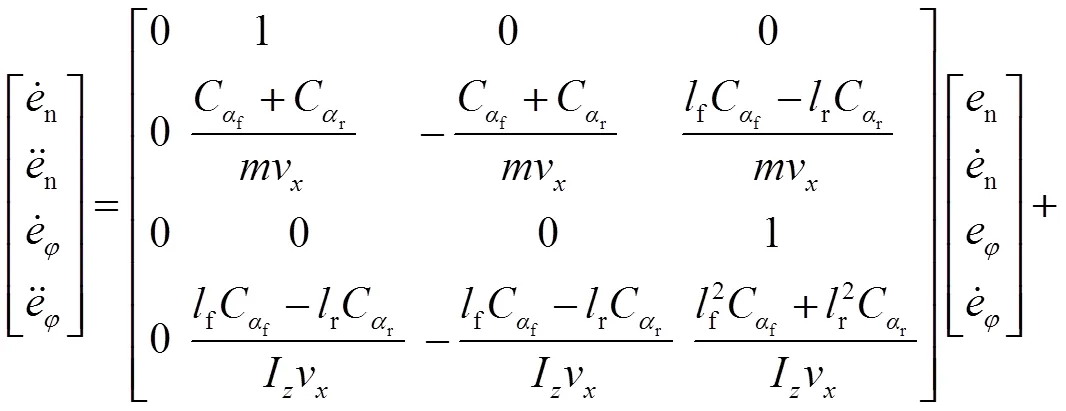
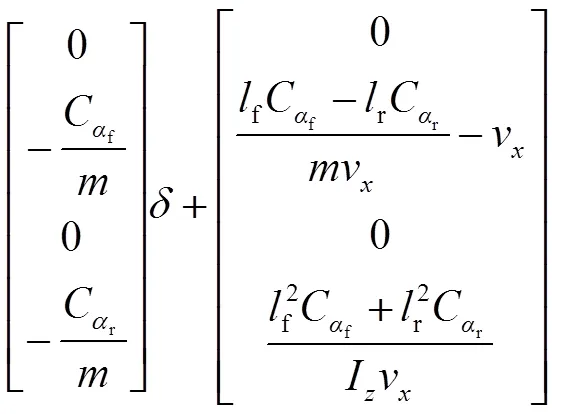
式（8）整理为

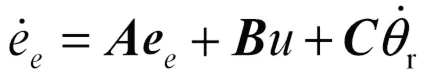
2 控制器和预瞄算法设计

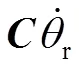
图3 含预瞄模块的横向控制模型

2.1 反馈控制

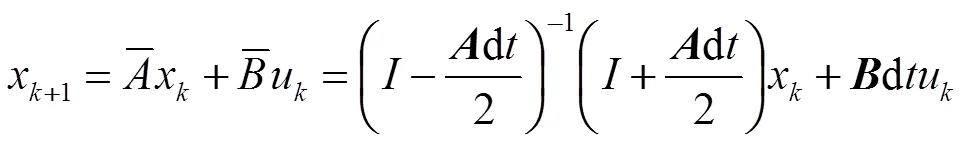
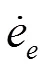
对式（11）进行离散化，得

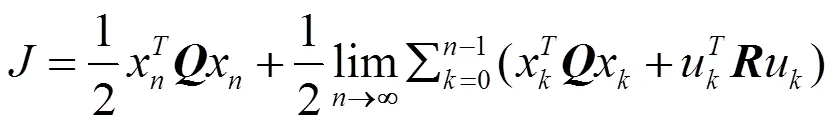
考虑在约束条件（10）下，应用极小值原理求性能函数最小值。

应用拉格朗日乘子法构造哈密尔顿函数：

式中，为正定半矩阵；为定半矩阵；则最优控制有唯一解：

u*=-Wx（14）

其中，的表达式为

=(+PB)-1PA （15）

为黎卡提方程，表达式为

=PA-(+PB)-1PA+（16）

2.2 前馈控制

利用反馈进行横向控制会形成稳态误差，为使横向位置误差为0，引入前馈以消除稳态误差。

令

=-Wx+δ（17）

将式（17）带入式（9）中进行整理，考察横向位置误差n，得

由n=0可得前馈输入为

由前馈和反馈共同作用的动力学横向控制系统如图4所示。

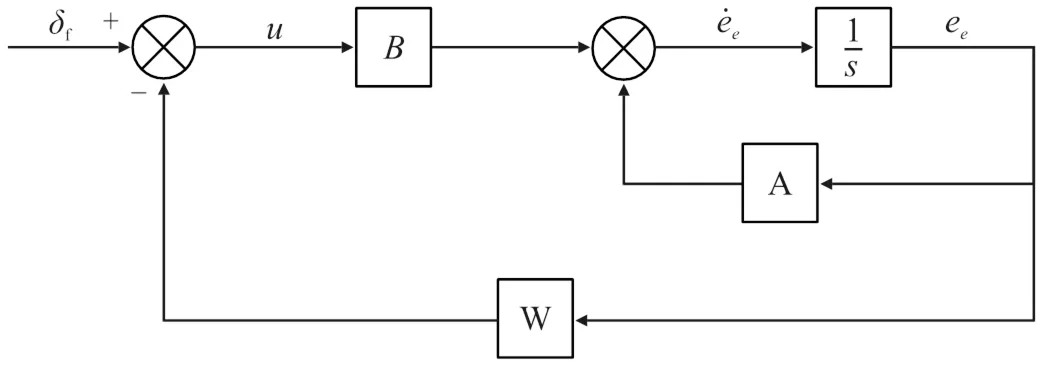
图4 前馈+反馈动力学横向控制模型框图

2.3 预瞄算法

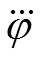
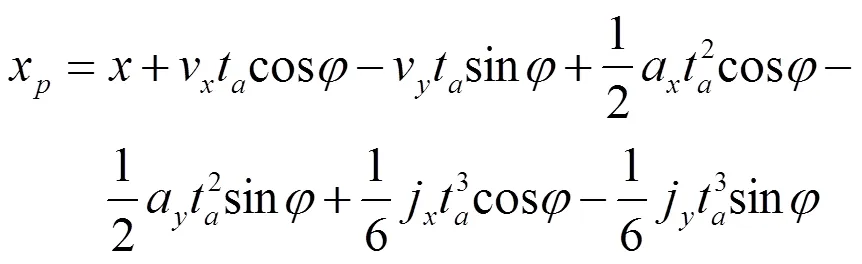
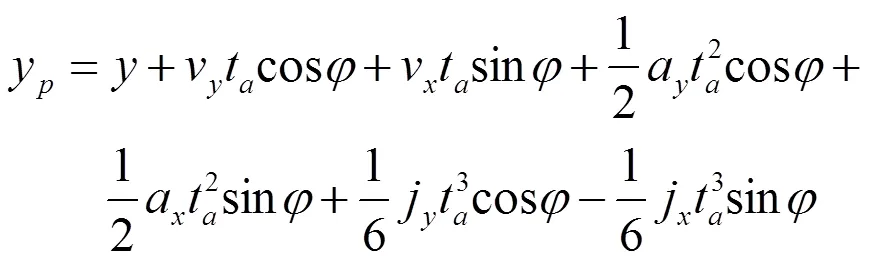
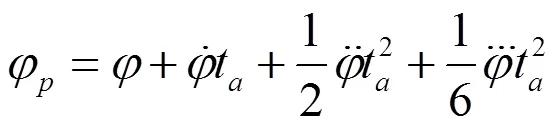
3 仿真结果与分析

为验证模型的跟踪效果，按前述算法在Simulink中建立数学模型，并在CarSim中建立车辆模型，通过联合仿真进行验证。车辆参数如表1所示。

表1 车辆参数

参数名数值 整车质量/kg1 413 轴距/mm2 910 质心到前轴距离/mm1 015 质心到后轴距离/mm1 860 绕z轴转动惯量/(kg·m2)1 536.7 初始车速/(m/s)10 节气门开度0.1

规划路径是一个半径为100 m的圆，起始位置为大地坐标系[0，10]处，车辆起始位置为大地坐标系[0，0]处，如图5所示。通过该路径考察车辆进入并跟踪稳态圆的效果。为更贴近真实物理环境，将控制输入给系统的滞后时间设定为100 ms。

为进行仿真效果对比，建立以车辆速度和横摆角速度为信号的预测模型，在相同条件下进行仿真测试。

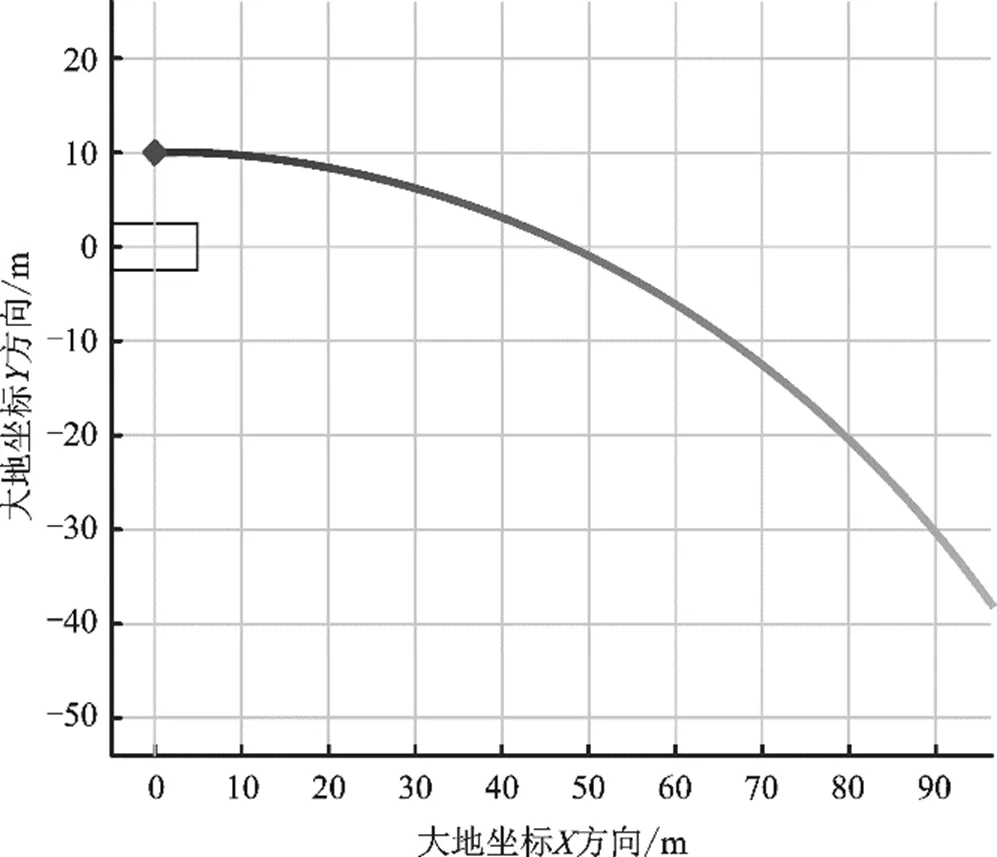
图5 车辆初始位置与轨迹形状

3.1 横向控制效果

利用横向位置的误差来衡量车辆追踪横向路径的控制效果。

从图6可以看到，在预瞄模型基于跃度信号的横向控制模型（下文用JERK模型替代）里，车辆的横向位置从初始时刻的-10 m处首次进入轨迹的稳态误差带（目标值±5%）内所用的上升时间为3.92 s；而基于速度信号的经典预瞄模型[6]（下文用VEL模型替代）用时4.16 s，JERK模型追踪横向位置误差的时间缩短了5.8%。

图6 横向位置追踪效果图

图7为图6的局部放大图。从图7可以看到，VEL模型在进入稳态误差带后，横向位置在较长时间内都没有收敛至0，且在6.5 s时仍有0.35 m的误差；而JERK模型则在6.5 s时仅残余0.05 m误差。

图7 横向位置追踪局部图

3.2 横摆控制效果

利用横摆角误差来衡量车辆追踪横摆控制效果。

从图8中可以看到，两个模型达到最大横摆角误差的时间基本一致。

JERK模型的误差峰值为44.3 deg，VEL模型的误差峰值为45.3 deg，基本接近。两种路径跟踪效果如图9所示。

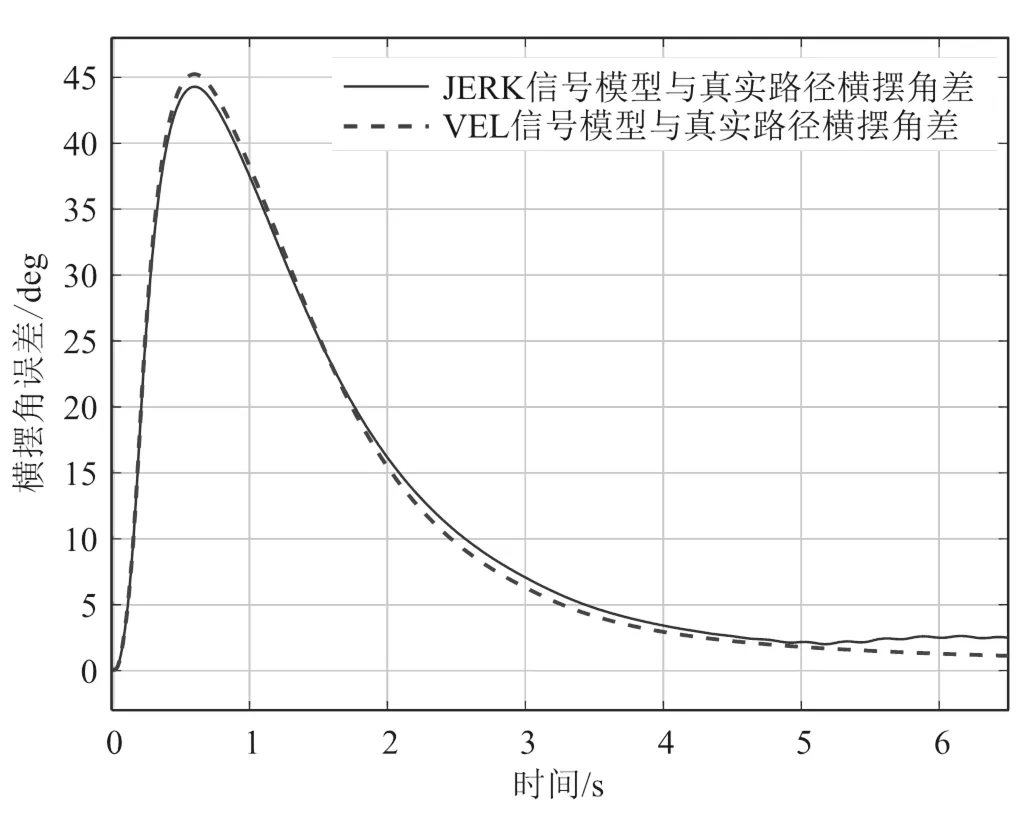
图8 横摆角追踪效果图

由于JERK模型的预瞄函数阶数更高，具有更强的预测未来的能力，所以横摆角存在较大的超前情况，当道路横摆角频繁变化的时候，JERK模型会与实际道路之间存在一个超前预测误差。

进一步分析，高阶信号带来的高响应性会导致更明显的超调，且当被控系统采用周期较长的时候，会带来更明显的波动。但考虑到波动量仅为0.01 deg/s，可忽略不计，如图10、图11所示。

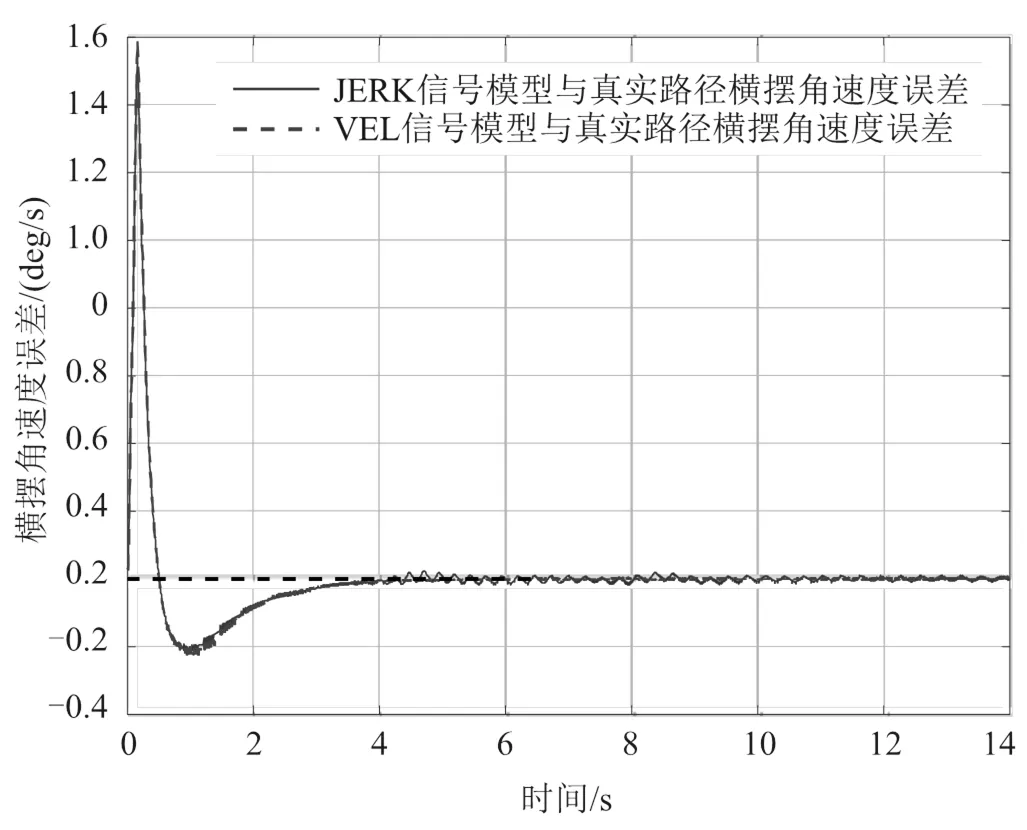
图10 横摆角速度误差对比图

图11 横摆角速度误差局部图

4 结论

本文通过建立车辆二自由度动力学误差方程，并利用线跃度和横摆角跃度构造预瞄模型的控制算法。利用LQR反馈控制和前馈控制的共同作用，实现车辆的横向误差跟踪闭环控制，以Simulink和CarSim为平台，建立联合仿真模型。

为验证基于跃度信号预瞄模型的横向控制效果，本文以进入并跟踪稳态圆为目标，并与基于速度信号的预瞄模型进行横向对比。通过对比JERK模型和VEL模型的横向位置误差和横摆角误差，可以看出基于跃度的信号模型能够使车辆更快、更平稳地进入目标轨迹，所设计模型的有效性得以验证。

此外，基于此预测模型，可以进一步对自动驾驶中的横向舒适性进行研究。

[1] ALFRAHEED M,ALICIA D,KLINGENDER M,et al. Longitudinal and Lateral Control in Automated Highway Systems:Their Past,Present and Future[C]//Intelligent Robotics and Applications-4th International Conference, ICIRA 2011.Aachen:Springer-Verlag,2011:589-598.

[2] 熊璐,杨兴,卓桂荣,等.无人驾驶车辆的运动控制发展现状综述[J].机械工程学报,2020,56(10):127-143.

[3] GAINING H,WEIPING F,WEN W,et al.The Lateral Track- ing Control for the Intelligent Vehicle Based on Adap- tive PID Neural Network[J].Sensors,2017,17(6):1244.

[4] 陶冰冰,周海鹰,王思山.自动驾驶车辆LQR轨迹跟踪控制器设计[J].湖北汽车工业学院学报,2017,31(4):1-6.

[5] 余志生.汽车理论[M].北京:机械工业出版社,2006.

[6] 满金.智能汽车路径跟踪控制的研究[D].杭州:浙江大学,2021.

Lateral Control of Automatic Driving Based on Jerk Signal

LI Muheng, LUO Yiyong, WANG Xiang, CHENG Xiang

( Automotive Engineering Research Institute, Guangzhou Automobile Group Company Limited, Guangzhou 511434, China )

Aiming at the lateral control of autonomous vehicle, a preview control based on jerk signal is proposed. The error model of 2-DOF vehicle dynamic is established, and the closed-loop lateral control model is composed by linear quadratic regulator(LQR) feedback control and feedforward control. Use CarSim and Simulink to simulate the vehicle entering and tracking a steady state circle. By analyzing the proxy such as lateral position error and yaw angle error, it is shown that the preview control has good results in accuracy of lateral control. Similarly, the tracking speed has also been significantly improved.

Autonomous vehicle; Preview control; Path tracking; Lateral control; 2-DOFvehicledynamics model

U495

A

1671-7988(2023)19-50-06

10.16638/j.cnki.1671-7988.2023.019.010

李沐恒（1989－），男，硕士，研究方向为车辆横向控制、转向系统性能开发，E-mail:624929885@qq.com。