基于等效电路模型的SOC估算

于 洋，徐长钊，毛理想，位翠翠，张 坤

基于等效电路模型的SOC估算

于 洋，徐长钊，毛理想，位翠翠，张 坤

（山东华宇工学院，山东 德州 253000）

锂离子电池相较于传统电池，具有能量密度大、没有记忆效应、循环性能优越、不含有毒有害物质等优点。有效管理电池的工作状态，准确估计电池荷电状态（SOC），对电池的安全工作以及延长其使用寿命具有重要意义。文章以18650三元锂电池作为研究对象，首先对锂离子电池的参数影响因素进行分析，然后对电池的等效电路模型进行讨论。考虑到传统卡尔曼滤波算法更多应用于线性系统，针对动力电池内部系统的非线性情况，需要对算法进行扩展，即需要将系统方程进行线性化处理。最后为了验证与测试估算系统的效果，在 MATLAB/Simulink中完成估算方案的编程，并对电池SOC估算系统进行仿真对比实验，经验证，恒流放电和混合功率脉冲特性两种工况下的算法误差均不超过8%。

动力电池；荷电状态；等效电路模型；仿真验证

随着近年来我国经济、科学水平的快速提升和发展，当今阶段的新能源汽车行业发展势头十分强劲，全球范围内涌现出许多不同种类的新能源汽车，而作为纯电动汽车的心脏，电池的性能将直接关乎纯电动汽车性能的优劣。换句话说，电池发展的未来也就是纯电动汽车的未来，二者之间有着千丝万缕的联系[1]。在目前市场上新能源电池的种类中，锂离子电池凭借其优越的性能在众多动力电池中获得越来越多的关注，并逐渐成为新能源汽车动力的主要供能装置。但是，锂离子电池也存在着一定的安全风险，当其处于过充、过放的状态时，会存在自然、爆炸的安全隐患。所以为了使锂离子电池长期处于安全高效的运行状态，建立一个有效的电池管理系统很有必要。在当今阶段，建立一个准确有效的电池模型对于电池荷电状态（State Of Charge, SOC）的估算非常重要，理论上，搭建的电池模型越精确，则对电池SOC估算精度方面的负面影响就越小[2]。

1 国内外锂电池研究现状

目前国内外针对锂电池的研究，都是建立在相应算法模型的基础上进行相关探索。考虑到动力电池工作过程中的影响因素包括外部温度环境、车况路况以及电池内部极化反应等，所以无法直接有效地测量电池SOC，而通过建立符合客观数据以及实际需要的电池模型，可以有效模拟电池内部化学反应状态引起的参数变化。因此，通过建立合适的电池模型来进一步估算电池SOC是十分有效的办法。

针对锂离子电池的SOC估算问题，目前国内外相关研究工作者取得了许多研究成果与研究创新。例如运用安时积分法与扩展卡尔曼滤波算法对锂离子电池组的荷电状态进行联合估算，结合各个算法的优点，有效提高了SOC估算精度；通过研究锂电池工作过程中的内阻发热特性，搭建锂电池热阻等效模型，利用最小二乘法以及自适应滤波算法对锂电池的热电耦合模型进行辨识与研究，提出更为有效的锂电池SOC估算方法。

当前国内外针对锂离子电池模型，最常见的大体可以分为三类：电化学模型、神经网络模型和等效电路模型。

1.电化学模型

电化学模型将锂电池简化为正电极、负电极、隔膜和电解液组成的系统。根据电池内部电化学反应、离子扩散和极化效应等电化学理论建立的电池模型。但是，这类传统的电化学模型在其建模过程中，存在计算量大、运算速度低、研究成本高、效率低等缺点。

2.神经网络模型

神经网络模型具有非线性、泛化能力强等特点，在应用时可以忽略复杂的电池内部结构与反应。常见种类包括：比例-积分-微分（Proportional- Integral-Derivative, PID）神经网络模型、反向传播（Back Propagation, BP）神经网络模型以及Elman神经网络模型等。

3.等效电路模型

等效电路模型是依据已有的锂电池充放电实验数据并利用电压源、电阻、电容等电子元件建立的模型。简单的等效电路模型能够极大地减少锂电池SOC估计的计算量，但是精度下降较多；而复杂的模型能够准确反映电池的输出特性，但会增加相应的计算量。所以中间如何进行平衡是在选取电池模型时重点考虑的问题，综合考虑模型精度与计算复杂度，选取等效模型作为本次课题研究工具。目前国内外常见的等效电路模型包含Rint模型、Thevenin模型、PNGV模型等。

2 电池模型建立及参数分析

2.1 电池模型的选择

电池等效的Rint模型是将电池等效为一个理想电源和电阻。如图1所示，Rint模型只能等效出电池的静态过程。

Thevenin模型如图2所示，与Rint模型相比较，Thevenin模型在电路中多串联了一组电阻和电容，既能等效出电池的动态和静态过程，也可以表达出电池的极化现象。

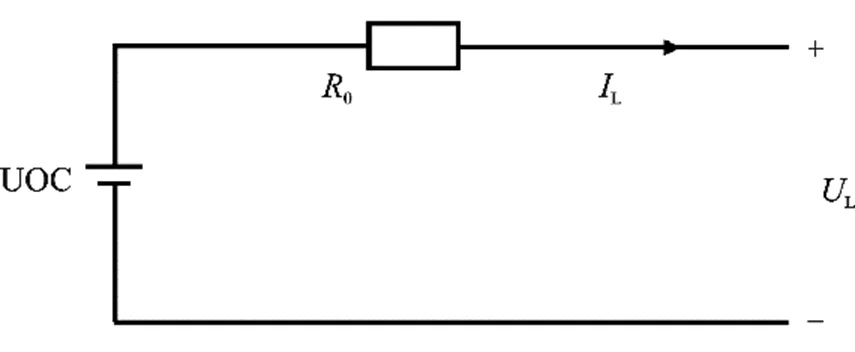
图1 Rint模型

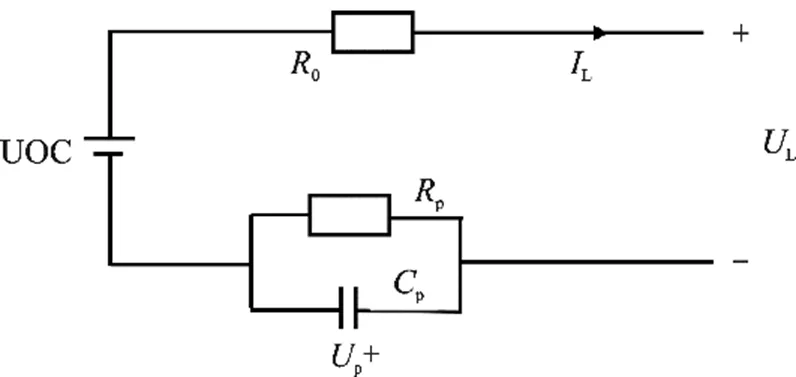
图2 Thevenin模型

PNGV模型如图3所示，与Thevenin模型不同的是，PNGV模型在等效电路中多串联了一个电容b，表达电流通过负载时由于电源电流累积造成的开路电压变化，其等效效果并不明显。

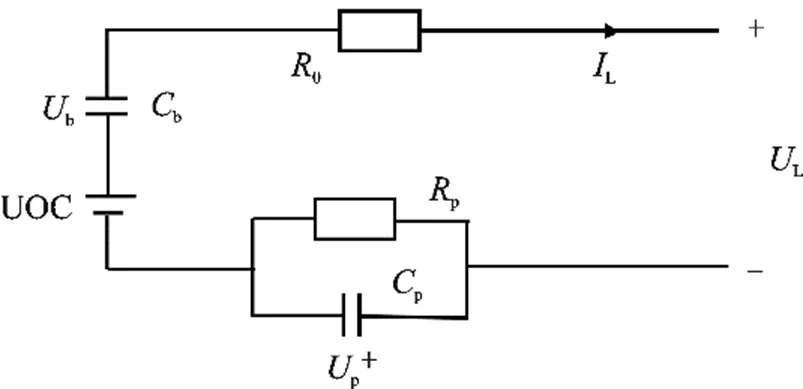
图3 PNGV模型

实际上模型的精度并不总是随着电阻-电容（Resistance-Capacitance, RC）网络数量的增加而提高，因为需要协调准确性和可靠性，目前来说一阶和二阶RC模型是最佳选择。考虑到高阶RC模型具有更好的鲁棒性，本次模型的选择是二阶RC等效电路模型，如图4所示。

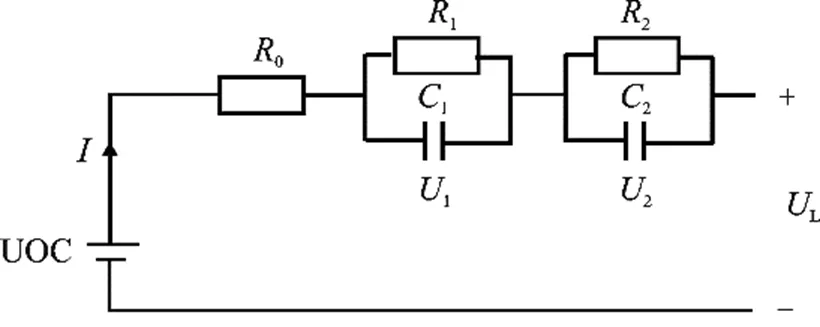
图4 二阶RC等效电路模型

该二阶RC等效电路模型由三部分组成：用UOC表示没有连接负载时动力电池的电压，即开路电压；欧姆内阻，即动力电池内部的接触电阻，使用R0表示；RC网络，使用极化内阻R1、R2和极化电容C1、C2来描述动力电池的极化特性[3]。

2.2 电池参数影响分析

2.2.1环境温度对电池容量的影响

锂离子电池的最佳工作温度是25～40 ℃。当温度低于5 ℃时，锂电池的放电容量会显著减少。

2.2.2放电倍率对电池容量的影响

将18650锂电池按照不同放电倍率进行恒流放电，相同温度下，通过不断增加放电倍率，观察电池放电容量的变化。随着放电倍率的提高，放电容量整体呈现先衰减后回升的趋势。

3 SOC估算方法

常见的估算方法大致分为四类：基于表征参数的方法、安时积分法、基于模型的方法以及基于数据驱动的方法。文章采用卡尔曼滤波算法进行研究。

3.1 卡尔曼滤波算法

卡尔曼滤波（Kalman Filter, KF）算法是一种最小方差意义上的最优估计方法，把需要估计的指标作为状态变量，把直接可测的系统输出作为观测量，采用递推法过滤掉噪声，不断地将估计值和测量值的权重进行重新分配，直到得出准确的状态值。最初的KF算法仅适用于线性系统，扩展卡尔曼滤波（Extened Kalman Filter, EKF）则对其进行了扩展，可用于非线性系统。

卡尔曼滤波算法在进行电池SOC估算时，是将SOC作为电池系统的状态变量，考虑到电池系统的非线性，使用卡尔曼滤波算法便无法满足精度的要求，这时需采用扩展卡尔曼滤波算法，即将系统方程做泰勒展开，进行线性化处理[4-6]。

1.电池系统线性化过程

对非离散线性系统，以ƒ(x-1,u-1)表示系统状态方程函数，以(x,u)表示系统观测方程函数，其系统方程的一般形式为

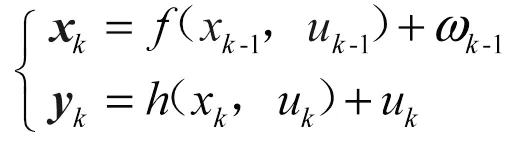
式中，为3维系统状态向量；为系统1维输入向量；为系统1维输出向量（或观测值）；ω-1为均值，取0，协方差为Q的系统噪声；υ为均值，取0，协方差为R的测量噪声。如果函数ƒ和都是线性的，那么所进行的算法就是经典的卡尔曼滤波算法；如果不是，那么则是扩展的卡尔曼滤波算法[7-9]。

由于本文的客观条件是非线性的，因此采用EKF算法对ƒ(x-1,u-1)和(x,u)用一阶泰勒展开线性化，即

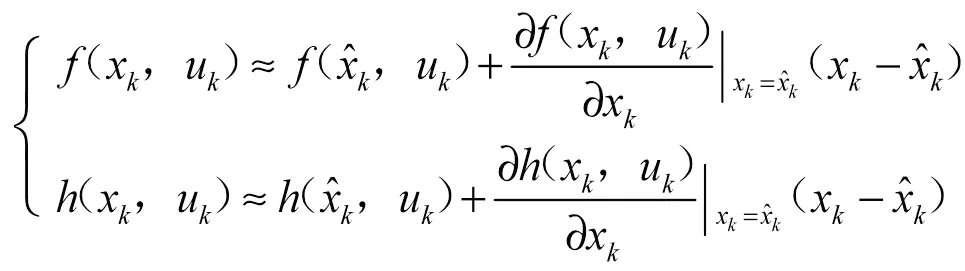
令

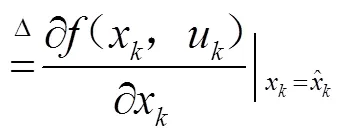
将式（2）代入式（1）可得线性化后的系统状态方程和观测方程为

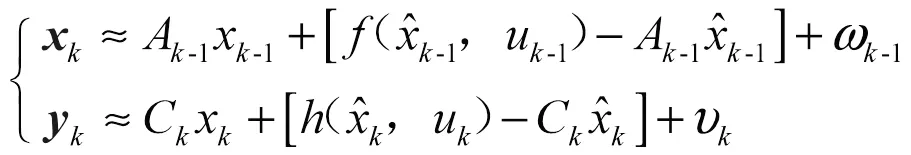
动力电池模型的线性离散化方程：

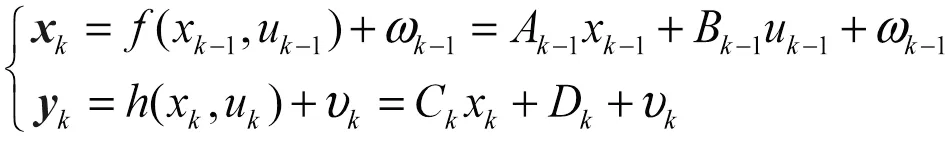
2.电池系统方程

卡尔曼滤波算法是一个不断循环迭代的过程，而安时积分法是进行有效卡尔曼滤波算法计算的一个基础。

安时积分函数模型：

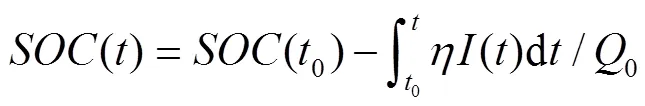
式中，为库伦效率；0为标定的电池实际容量。

离散化后可得

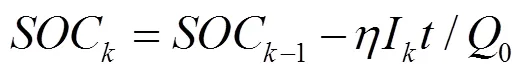
选择1、2和作为状态变量，选择U作为观测量，可得线性化后的系统状态方程：

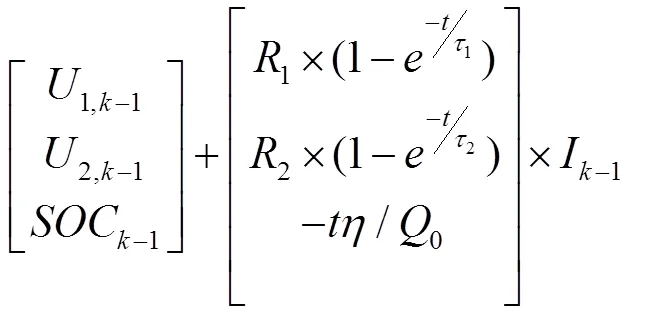
输出方程：

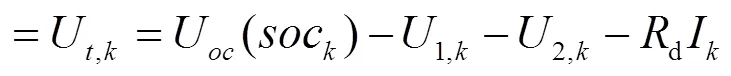
因此，由状态方程得出系统矩阵：

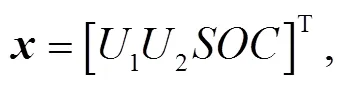
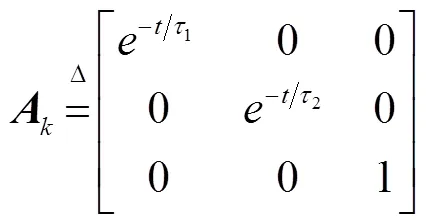
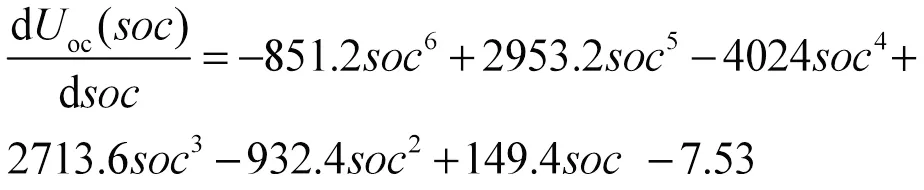
基于上述系统方程，建立应用EKF算法的SOC估计流程。

3.应用EKF算法的SOC估计

应用EKF算法的SOC计算流程如图5所示[10-11]。

基于EKF算法的SOC估计方法的详细计算流程如下：

2）先验估计－预测：从(-1)+到()-推算出状态估计和状态误差协方差估计，线性化后的离散时间更新方程表示如下：

预测状态：

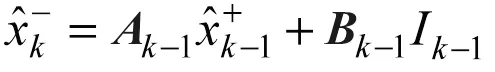
误差协方差：

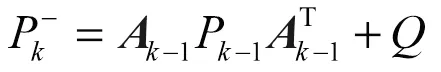
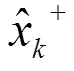
预测系统输出：

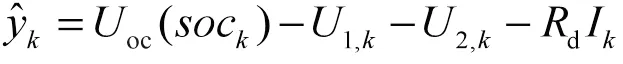
新息矩阵：

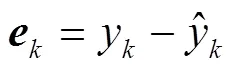
卡尔曼增益矩阵：

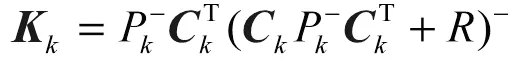
状态估计测量更新：

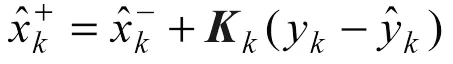
误差协方差测量更新：

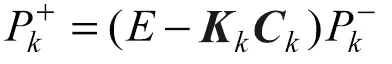
4）时间尺度更新：将（）+的状态和协方差矩阵作为输出，准备（+1）的状态估计，其中，=1,2,…。采用式（10）－式（16）就可以通过EKF算法的迭代过程，实现对动力电池的SOC估计。

图5 EKF算法的计算流程图

3.2 安时积分和自适应扩展卡尔曼滤波的联合估算方法

在传统EKF估算方法中，系统过程噪声方差是高斯白噪声，观测噪声方差也是高斯白噪声，二者都固定，与现实不一样，因此，采用自适应扩展卡尔曼滤波，引入噪声信息协方差匹配算法，该算法使得系统噪声和观测噪声协方差自适应更新，从而使得状态误差协方差和卡尔曼增益都得到更新。为了保证系统的SOC估算精度，同时又要兼顾算法的简化程度，在放电后期引入安时积分是最为合适的选择。

3.2.1自适应EKF算法的SOC估计

基于非线性离散电池系统状态方程，建立应用自适应EKF算法的最优估计流程，如图6所示。

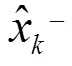
越接近0，说明更看重状态方程的估算值；如果越接近1，说明更看重电压测量值的修正作用[12]。计算过程如下：

1）初始化：设置状态观测器的初始值0,0,0,0。

2）先验估计－预测：从（-1）+到（）-推算出状态估计和状态误差协方差估计，系统的时间更新方程表示如下：

系统状态预估：

误差协方差预估：

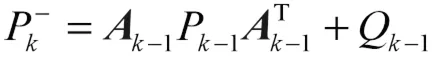
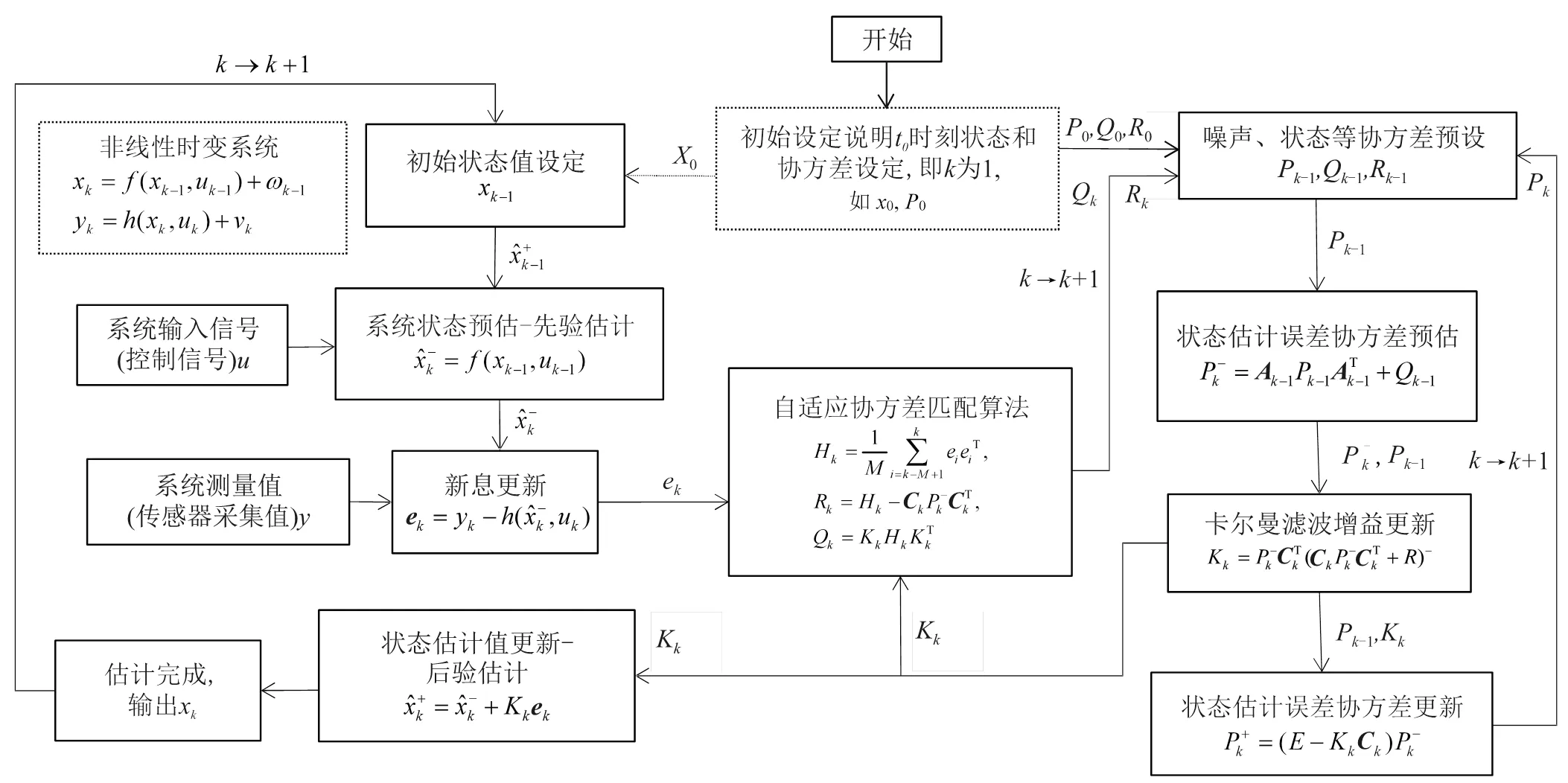
图6 自适应EKF算法的计算流程图

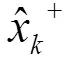
新息矩阵：

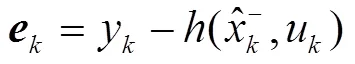
卡尔曼增益矩阵：

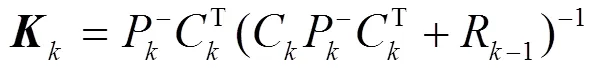
自适应噪声协方差匹配：

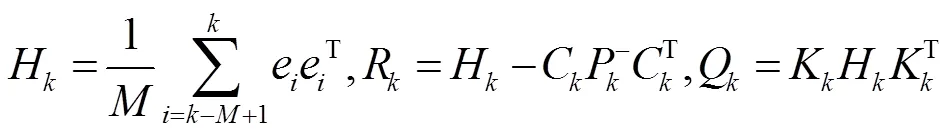
系统状态修正：

误差协方差修正：

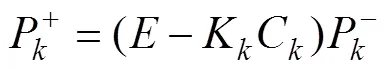
4）时间尺度更新：将（）+的状态和协方差矩阵作为输出，准备（+1）进行的状态估计。采用式（17）－式（23）就可以通过自适应EKF算法的迭代过程，实现对动力电池的SOC估计。

3.2.2安时积分的后期修正

方案如下：1代表AEKF估算值，2代表安时积分估算值，代表AEKF估算所占的权重，>0.2时，模型精度高，采用AEKF进行估算，=1；在0.1到0.2之间时，模型精度逐渐下降，估算方案由AEKF过渡到安时积分，的值由1线性变化到0；当SOC低于0.1时，=0，采用安时积分进行估算。流程如图7所示。

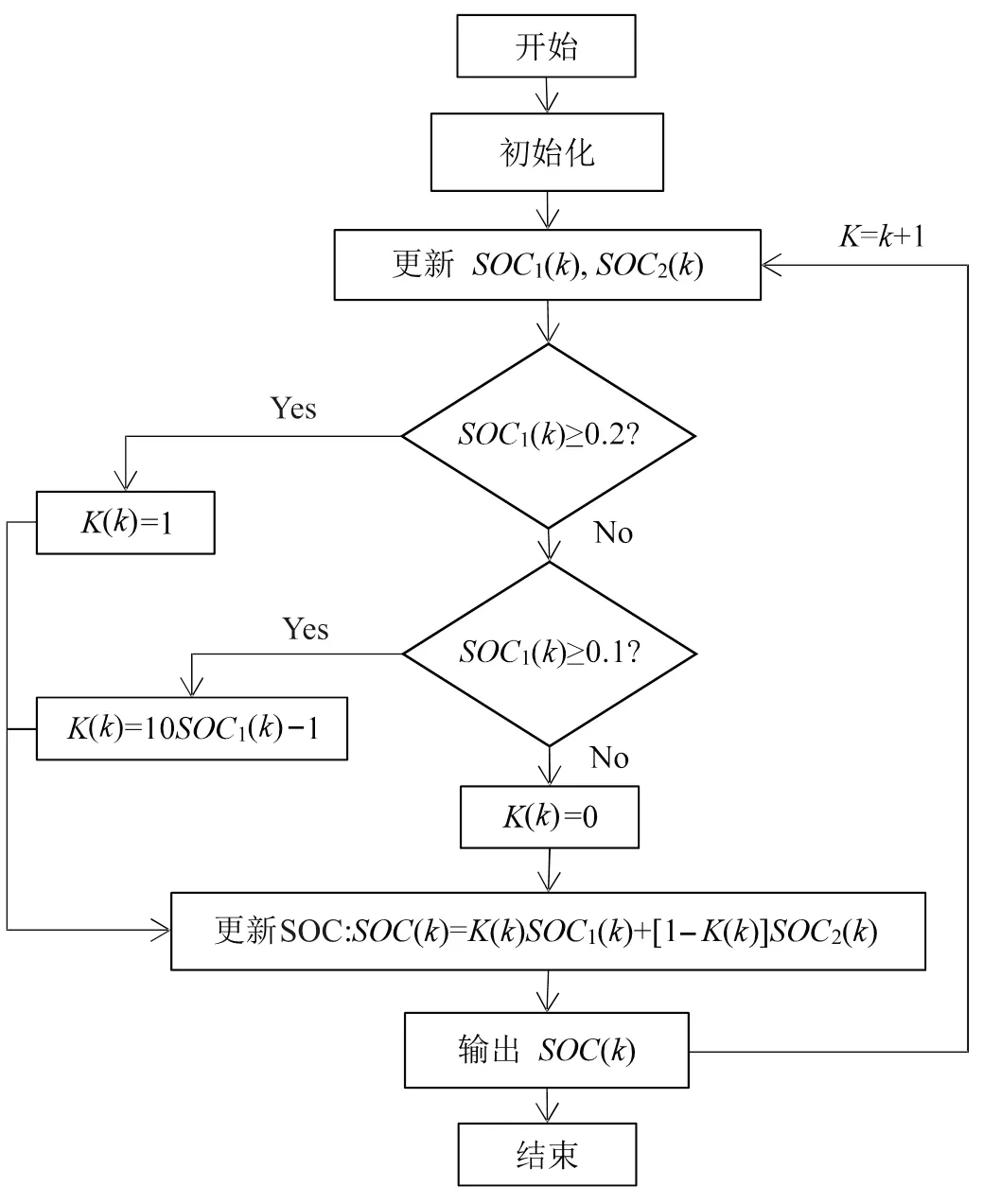
图7 安时积分和AEKF联合估算流程图

4 SOC估算系统的测试与验证

上述章节建立二阶RC等效电路模型、基于EKF的SOC估算系统、联合安时积分和AEKF的SOC估算系统。本文在算法的设计阶段利用计算机进行仿真，根据仿真结果可以及时地调整模型和参数。本章将在不同工况下对其进行仿真验证以及对比分析。

为了验证本文搭建的SOC估算系统，利用电池测试系统获取电池不同工况下的测试数据，将数据导入MATLAB/Simulink工具箱中，在MAT- LAB/Simulink中完成估算方案的编程，进行电池SOC估算系统的仿真对比实验。

4.1 恒流放电工况验证

在SOC初始值准确的情况下，对SOC估算系统进行仿真：在25 ℃下，以1 C电流恒流放电，采用安时积分处理实验数据得到SOC理论值，使用扩展卡尔曼滤波算法来估算电池SOC，实验数据如图8所示。采用安时积分和自适应扩展卡尔曼滤波联合估算方法估计电池SOC，估算结果如图9所示。

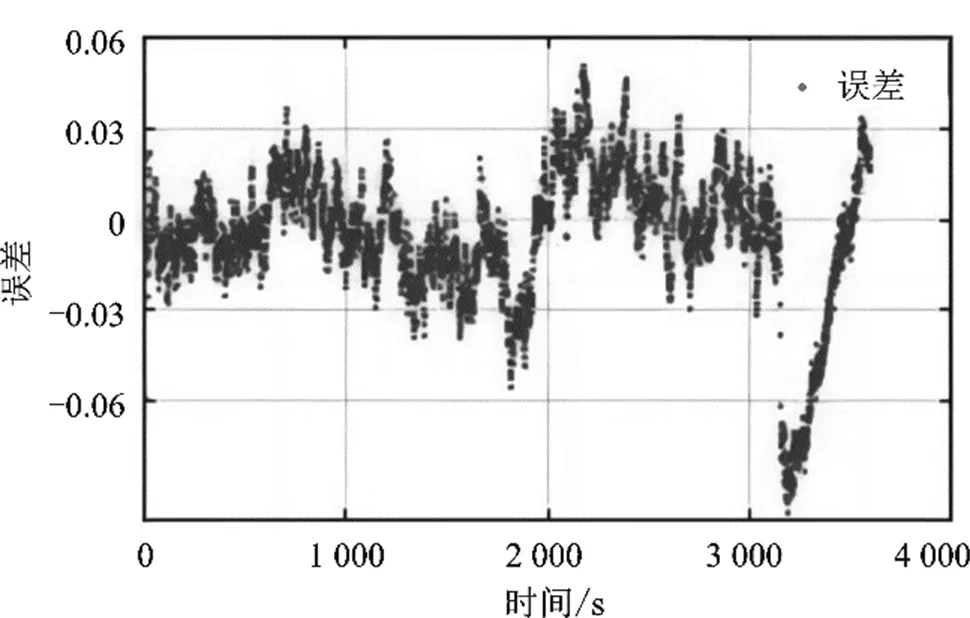
图8 EKF误差曲线

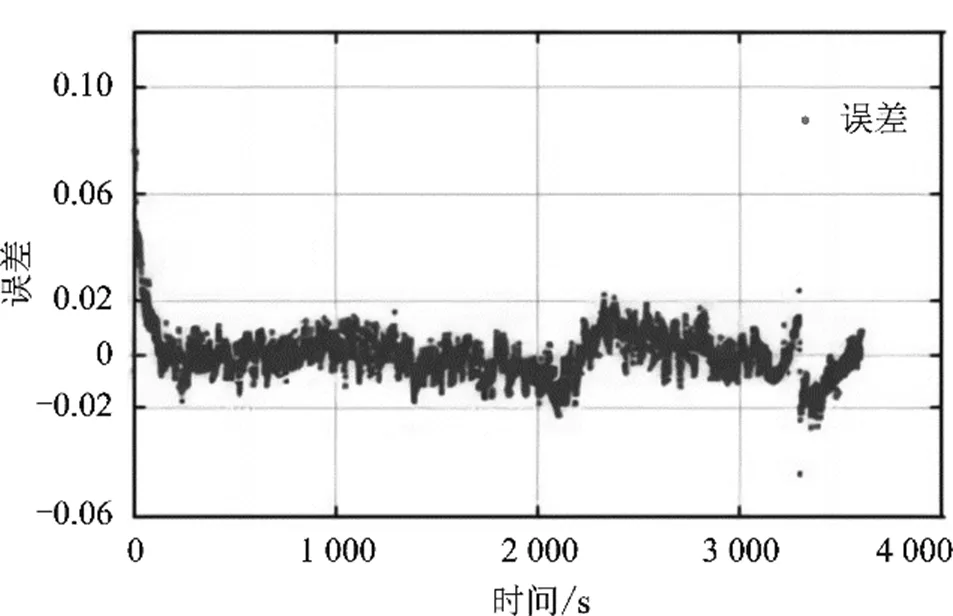
图9 联合估算误差曲线

放电刚开始时，联合估算方案的误差比EKF估算误差大，但是随着自适应调整的变化，联合估算方案的误差迅速收敛，且波动幅度更小。具体统计数据如表1所示。

表1 基于恒流放电工况的SOC误差绝对值统计分析

对象最大误差最小误差平均误差均方根误差 EKF误差0.095 1200.016 790.016 59 联合估算误差0.11800.005 2160.006 9

4.2 HPPC工况验证

混合脉冲功率特性（Hybrid Pulse Power Char- acteristic, HPPC）工况测试是由多组电流脉冲测试组成的，每组电流脉冲测试的SOC相差10%。在电池进入电化学与热平衡后才允许进入下一组测试，一般间隔1 h时间。测试目的是确定电池包在电流脉冲工况中的动态功率能力。

接下来在25 ℃下进行HPPC测试，选用1 C充电方式充满电的电池，首先在SOC为100%状态时对电池进行10 s放电，放电倍率为1 C，然后搁置40 s，再对电池进行10 s的1 C反馈充电，搁置40 s，然后将电池以1 C倍率放电至SOC为90%，静置30 min后进行为90%时的HPPC测试，重复以上步骤至放电截止电压。实验数据如图10所示。

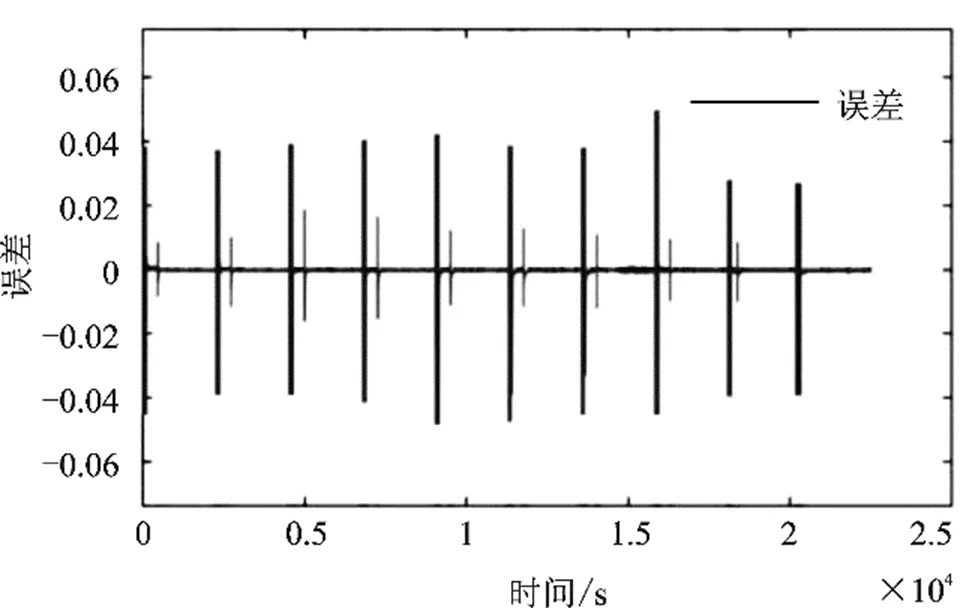
图10 电压误差曲线

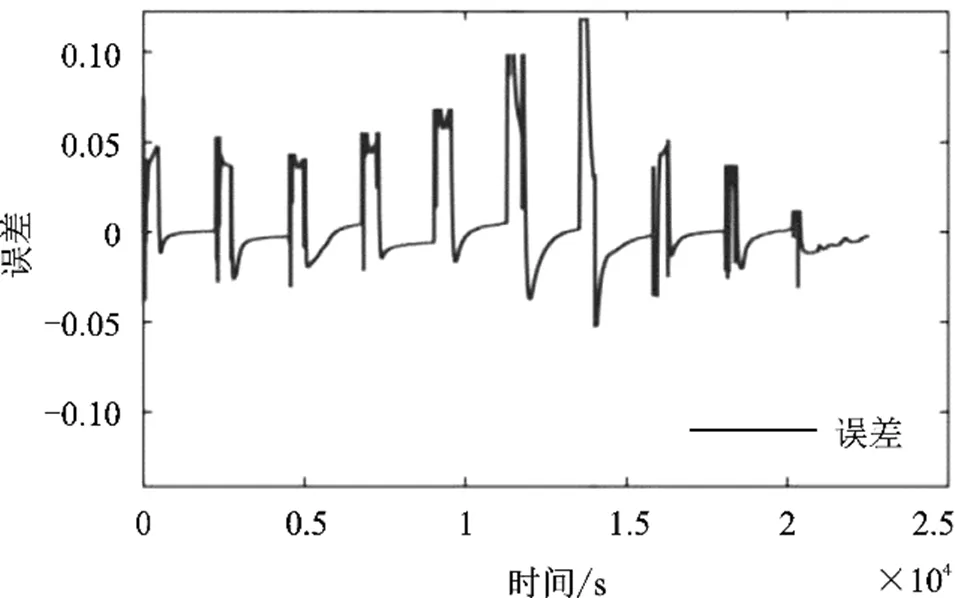
图11 联合估算SOC误差曲线

如图11所示，在整个HPPC工况下，平均误差不超过8%。具体统计数据如表2所示。

表2 HPPC工况下的误差数据统计

对象最大误差最小误差平均误差均方根误差 电压误差0.050 100.018 0130.008 123 联合估算误差0.115 100.038 310.039 14

5 总结

通过对所搭建的SOC估算系统进行恒流放电工况和HPPC工况的仿真验证，可以观测到在恒流放电工况下，联合估算方案的SOC平均估算误差比传统EKF的要小，且都不超过8%；而在HPPC工况下的SOC平均估算误差不超过8%。

[1] 邓鹏毅,彭忆强,蔡云,等.新能源汽车产业技术及发展趋势[J].西华大学学报(自然科学版),2017,36(4): 34-45.

[2] 申彩英,申丽军.基于CAN总线的电池管理系统研究 [J].电源技术,2017,41(11):1556-1557,1583.

[3] 李百华,郭灿彬,钟其水,等.电动汽车锂电池戴维南等效电路模型参数辨识研究[J].微型机与应用,2017,36(1):83-85,88.

[4] 胡晓松,唐小林.电动车辆锂离子电池建模方法综述[J].机械工程学报,2017,53(16):20-31.

[5] 陈息坤,孙冬.锂离子电池建模及其参数辨识方法研究[J].中国电机工程学报,2016,36(22):6254-6261.

[6] 张卫平.雷歌阳.张晓强.锂离子电池等效电路模型的研究[J].电源技术,2016,40(5):1135-1138.

[7] 秦良艳.基于卡尔曼滤波的动力锂电池单体SOC估算方法研究[D].重庆:重庆邮电大学,2020.

[8] 毛华夫,万国春,汪镭,等.基于卡尔曼滤波修正算法的电池SOC估算[J].电源技术,2014,38(2):298-302.

[9] 胡敏康.基于改进卡尔曼滤波算法的锂离子电池荷电状态估计算法研究[D].合肥:合肥工业大学,2020.

[10] 蒋佑煊,王春雷,孔继周,等.锂离子电池的SOC估算方法的研究进展[J].电源技术,2018,42(2):296-300.

[11] 刘文涛.电动汽车动力电池SOC测量技术[J].汽车工业研究,2018(7):55-60.

[12] 熊瑞.动力电池管理系统核心算法[M].北京:机械工业出版社,2018.

[13] 夏飞,王志成,郝硕涛,等.基于改进扩展卡尔曼粒子滤波算法的锂电池SOC估计[J].系统仿真学报,2020, 32(1):44-53.

SOC Estimation Based on Equivalent Circuit Model

YU Yang, XU Changzhao, MAO Lixiang, WEI Cuicui, ZHANG Kun

( Shandong Huayu University of Technology, Dezhou 253000, China )

Compared with traditional batteries, lithium-ion batteries have the advantages of high energy density, no memory effect, superior cycle performance, and no toxic and harmful substances. Effectively managing the working state of the battery and accurately estimating the state of charge (SOC) of the battery are of great significance for the safe operation of the battery and prolonging its service life. In this paper, 18650 ternary lithium battery is taken as the research object. Firstly, the influencing factors of lithium-ion battery parameters are analyzed, and then the equivalent circuit model of the battery is discussed. Considering that the traditional Kalman filter algorithm is more applied to linear systems, for the nonlinear situation of the internal system of the power battery, needs to extend the algorithm, that is, the system equation needs to be linearized. Finally, in order to verify and test the effect of our estimation system, the estimation scheme is programmed in MATLAB/Simulink, and the battery SOC estimation system is simulated and compared. It is verified that the algorithm errors under constant current discharge and hybrid pulsepower characteristic conditions are not more than 8%.

Power battery; State of charge; Equivalent circuit model; Simulation verification

U469.72

A

1671-7988(2023)19-22-08

10.16638/j.cnki.1671-7988.2023.019.005

于洋（1989－），男，硕士研究生，工程师，研究方向为新能源汽车动力电池管理，E-mail:jsanjian@sina.com。

德州市电动汽车动力控制与调试重点实验室（6）。