基于T-S模糊理论的车辆主动转向系统多目标控制

2023-10-19马新波仝佳森

南阳理工学院学报 2023年4期

马新波, 仝佳森, 解芳

(南阳理工学院智能制造学院河南南阳 473004)

0 引言

作为车辆动力学领域的重要组成部分,转向稳定性主要侧重于车辆的横摆运动和侧翻运动,其性能直接影响车辆的操纵稳定性和主动安全性[1-2]。为了降低驾驶员的操纵负担并提高车辆的主动安全性,本文引入了主动转向系统。主动转向系统可以在驾驶员输入转角的基础上主动地叠加一个额外的转角,从而实现横摆力矩控制,以改善车辆转向稳定性[3-6]。

虽然主动转向系统能通过主动转角补偿的方式实现横摆力矩控制,但是车辆本身复杂的非线性特性使主动转向系统在某些特定的工作条件下无法产生恰当的横摆力矩。例如,当侧向加速度过高时,车轮转角的输入不能产生有效的横摆力矩,从而造成转向稳定性失控[7-8]。主动转向系统对车辆转向稳定性的影响与其有效工作区间密切相关。因此,在引入主动转向系统时,需对其有效工作区间进行详细的分析。

主动转向系统的主动转角补偿是通过相应的控制算法得到的,现有的研究大多以横摆角速度作为控制目标来表征转向稳定性。事实上,车身侧偏角也是衡量车辆转向稳定性的一个重要指标。当车身侧偏角较小时,车辆动力学特性主要取决于横摆角速度;当车身突然发生严重侧偏时,车辆侧偏角急剧增加,横摆角速度不再是主要的动力学性能评判指标,需考虑车辆侧偏角[9]。因此,车辆转向稳定控制是多目标控制问题,包含横摆角速度和车辆侧偏角两个控制变量。

在多目标控制领域,线性二次型调节器(linear quadratic regulator,LQR)是处理线性或非线性系统的经典方法[10-11]。现存的研究中多以二自由度线性侧向模型作为控制器设计的对象,这忽略了车辆侧向动力学系统中的非线性问题,控制效果的准确性不能满足要求。因此,在设计LQR控制器时,需充分考虑车辆操纵模型中轮胎的非线性问题。现有的经典轮胎模型基本上能准确描述轮胎的非线性,但是其复杂的非线性计算过程难以满足控制器的快速响应要求。为了同时保证模型的准确性和控制率的简便性,可采用T-S(Takagi-Sugeno)模糊理论修正车辆操纵模型,将非线性模型线性化处理后,得到非线性主动转向系统模型并进行多目标控制器的设计[12]。T-S模糊理论是将一个复杂的非线性系统用几个简单的线性模型通过局部逼近的方法进行加权求和的形式代替[13-15]。目前,T-S模糊理论已经用于车辆主动悬架系统的多目标控制中,以描述车辆垂向模型中簧载质量和非簧载质量的变化[15]。

综上所述,本文采用了基于T-S模糊理论的LQR多目标控制器来实现主动转向系统的横摆力矩控制,从而提高车辆的转向稳定性。首先,对主动转向系统的工作区间进行了详细分析与界定,并在此区间内采用T-S模糊理论将复杂的非线性轮胎进行线性化处理,以保证主动转向系统模型的精确性和简便性;之后综合考虑了横摆角速度和车辆侧偏角这两个控制变量,在基于T-S模糊理论的主动转向系统模型基础上设计了LQR多目标控制器;最后通过Simulink和CarSIM联合仿真,验证了该主动转向系统控制方法的有效性和实用性。

1 基于T-S模糊理论的主动转向系统模型

1.1 二自由度操纵模型

描述侧向运动和横摆运动的二自由度操纵模型可反映车辆的转向特性(如图1所示)。此模型反映了在纵向速度恒定时,横摆角速度、车辆侧偏角和输入转向角之间的关系。通过建立直角坐标系,车辆的侧向运动和横摆运动可以描述为

图1 二自由度操纵模型

(1)

其中,m为车辆的质量,Iz是车辆相对于转轴的转动惯量,vx是车辆质心处的纵向速度,β是车辆侧偏角,γ是横摆角速度,Cf和Cr分别是前、后轮的侧偏刚度,δ为前轮转向角,lf和lr分别是车辆质心到前、后轴之间的距离。

(2)

1.2 主动转向系统模型

由于轮胎的非线性,二自由度操纵模型中的前、后轮的侧偏刚度Cf和Cr均应为变量。在垂向力一定的情况下,Cf和Cr的值随着前轮转向角的变化而变化。为了描述轮胎侧偏刚度的变化,需对主动转向系统的工作区间进行界定,之后采用T-S模糊理论建立主动转向系统模型。

主动转向系统是通过引入额外转角的方式来改变横摆力矩,从而提高车辆转向稳定性。其中,横摆力矩是由前后轮胎侧向力对矩心力矩的差值引起的,而前后轮胎侧向力又与轮胎侧偏角密切相关。当侧偏角较小时,轮胎侧向力几乎与侧偏角成正比,该区间为线性区域;随着侧偏角的增大,轮胎侧向力对侧偏角的响应越来越弱,该区间为过渡区间;当侧偏角达到一定值时,轮胎侧向力基本保持不变,该区间为饱和区间。为了确保主动转向系统的有效运行,其工作区间被界定在线性区间和过渡区间(如图2)。

图2 主动转向系统有效工作区间

在有效工作区间内,随着轮胎侧偏角的增大,轮胎侧偏刚度值逐渐从最大值变化到最小值。具体来说,前、后轮胎侧偏刚度的变化范围分别为[Cfmin,Cfmax]和[Crmin,Crmax]。采用T-S模糊理论,前、后轮胎侧偏刚度可以表示为

(3)

由此,可以得到如下的隶属度函数

(4)

相应的模糊规则包含4条。

其中A1(t)和B1(t)可以通过把A(t)和B(t)中的Cf和Cr分别替换为Cfmax和Crmax的方式得到。

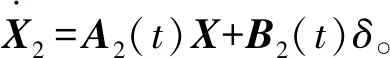
其中A2(t)和B2(t)可以通过把A(t)和B(t)中的Cf和Cr分别替换为Cfmax和Crmin的方式得到。

其中A3(t)和B3(t)可以通过把A(t)和B(t)中的Cf和Cr分别替换为Cfmin和Crmax的方式得到。

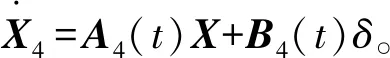
其中A4(t)和B4(t)可以通过把A(t)和B(t)中的Cf和Cr分别替换为Cfmin和Crmin的方式得到。

基于上述的模糊规则,主动转向系统模型可以表示为

(5)

该主动转向系统模型充分考虑了轮胎的非线性特性,并用T-S模糊理论构建了线性模型,简化了模型的复杂性。根据轮胎侧偏角的变化,主动转向系统模型中的权重系数hi(i=1,2,3,4)值也会随着隶属度函数M1(Cf)、M2(Cf)、M1(Cr)和M2(Cr)值的变化而变化,从而实时构建不同的状态方程。

2 多目标控制器设计

车辆转向稳定性控制是一个多目标控制问题,需综合考虑横摆角速度和车辆侧偏角,使其尽可能接近理想值。控制器可在已建立的主动转向系统模型基础上进行设计。

2.1 理想值计算与分析

横摆角速度和车辆侧偏角的理想值可在稳定行驶条件下计算得到,此时横摆角速度和车辆侧偏角为恒定值,其变化率为0。根据式(1)给出的二自由度操纵模型,可以计算出横摆角速度和车辆侧偏角的理想值分别为

(6)

2.2 LQR控制器设计

结合主动转向系统模型状态方程和控制目标理想值,LQR控制器的二次性能方程可以表示为

(7)

式中:η1和η2分别表示横摆角速度和车辆侧偏角的权重,T为评估时长,N1、N2和N3分别为状态变量、控制变量和交叉项的权重矩阵。使LQR控制器的二次性能方程最小化的解为

(8)

式中的矩阵P可以通过求解如下的方程获得

(9)

3 仿真与分析

为了验证所提出的基于T-S模糊理论的LQR多目标控制器的主动转向系统的有效性,采用MATLAB和CarSIM的联合仿真的形式进行了正弦停滞测试。其中MATLAB部分进行了多目标控制器的设计,这是基于T-S模糊理论的主动转向系统模型进行的,而CarSIM部分调用了整车模型。控制器的输出转向角和方向盘转角可作为CarSIM部分的输入,而CarSIM部分呈现出的车辆状态,比如横摆角速度和车辆侧偏角,又反馈到MATLAB部分的多目标控制器中,相关车辆参数如表1所示。

表1 车辆参数与数值

正弦停滞测试实验中,输入的方向盘转角如图3所示,该转角是由一个固定频率为0.7 Hz的正弦函数和一个0.5 s的迟滞组合而成,方向盘最大转角为270°。另外,被动转向系统和传统的多目标控制主动转向系统分别作为对比案例,被动转向系统指的是不考虑主动转向系统并且不施加任何控制的车辆系统,而传统的多目标控制主动转向系统指的是在不考虑主动转向系统的工作区间和轮胎的非线性特性的前提下进行多目标控制的车辆系统。相应的测试结果如图4所示,包含横摆角速度、车辆侧偏角和侧向加速度,这3个指标可用于评估车辆的转向稳定性。从测试结果可以看出,相比较于被动转向系统,主动转向系统所产生横摆角速度、车辆侧偏角和侧向加速度较小,这是由多目标控制器的闭环控制作用引起的。相比较于传统的多目标控制主动转向系统,基于T-S模糊理论的LQR多目标控制器的主动转向系统能更快地达到稳定状态,这是因为T-S模糊理论部分充分考虑了主动转向系统的工作区间和轮胎的非线性特性,从而提高了多目标控制器的准确性。然而,相比较于传统的多目标控制主动转向系统,基于T-S模糊理论的LQR多目标控制器的主动转向系统在输入迟滞区间附近(2.5～3.5 s)存在较大的波动,这是因为较大的轮胎侧偏角使主动转向系统在过渡区间内工作,在此区间内,轮胎侧偏角的变化必然引起主动转向系统模型状态方程的变化,从而引起相应的状态参数波动。

图3 正弦停滞测试的方向盘转角输入

图4 正弦停滞测试的测试结果

表2给出横摆角速度、车辆侧偏角、侧向加速度的峰值和均方根值在主动转向系统作用下的下降情况。从表中可以看出,相比较于被动系统,传统的多目标控制主动转向系统的横摆角速度、车辆侧偏角和侧向加速度的峰值分别下降了22.53%、26.71%和17.54%,均方根值分别下降了27.63%、43.37%和31.11%,所提出的基于T-S模糊理论的LQR多目标控制器的主动转向系统的横摆角速度、车辆侧偏角和侧向加速度的峰值分别下降了14.63%、20.67%和14.17%,均方根值分别下降了22.39%、53.29%和27.21%。