盘管式核主泵高压冷却器的流致振动分析

2023-10-18韩冬傲浦承皓

动力工程学报 2023年10期

韩冬傲, 金刚, 浦承皓

(生态环境部核与辐射安全中心,北京 100082)

高压冷却器是核反应堆冷却剂泵(核主泵)的重要配套设备,用于向核主泵的轴密封系统和径向水润滑轴承提供高压注入水和冷却水,其管程为核岛一回路承压边界的一部分,因此保持高压冷却器的运行性能和结构完整性,对于核主泵以及核岛一回路安全、稳定运行有着重要的意义。尤其是高压冷却器的管程,属于核一级部件,是需要重点考察的对象。

当冷却介质流经高压冷却器的换热管束时,将与管束相互耦合引发流致振动,如不进行有效控制,可能会使设备发生破损。因此,有效防止管束发生流致振动破坏,是高压冷却器设计过程中需要考虑的关键问题。

引起传热管流致振动的主要机理包括流弹失稳、漩涡脱落、湍流抖振和声共振四类。其中,流弹失稳是由于在动态流体载荷与传热管振动相互作用下,当传热管自身阻尼消耗的能量小于冷却剂作用于传热管的能量时,管子将产生不可收敛的振动,从而导致结构破坏。湍流抖振是由于冷却剂流动引起的湍流随机脉动压力作用在传热管表面产生振动,属于随机振动,通常湍流抖振的振幅相对较小,但在长期作用下会导致传热管的疲劳累积。漩涡脱落是由于传热管表面周期性脱落漩涡所产生的周期性流体载荷引起的,如果漩涡脱落的频率和传热管的固有频率重合或者相近,则会发生共振,振幅将会快速放大,从而破坏传热管结构。声共振是由于高速气体在传热管内流动时产生了可压缩性,流体压力按照声速传播,声波的振动频率和结构频率相互耦合导致结构破坏,本文研究的盘管式冷却器由于是液体工质,因此可不考虑声共振问题。

流致振动作为管壳式换热器设计中需要考虑的重要因素,许多学者和科研机构已进行了很多相关研究。例如,符兴承等[1]对管壳式换热器因流致振动引起结构破坏的形式进行了分析,并根据不同的振动机理提出了相应的应对措施。郎红方等[2]按照管式换热器制造商协会(TEMA)规范[3]中的流致振动分析方法和判定准则,对某核电厂2级和3级管壳式换热器进行了分析;叶泉流等[4]对核级换热设备流致振动分析的方法、校核依据进行了研究和探讨;齐欢欢等[5]建立了流体力与传热管振动的耦合模型,即“新尾流振子模型”,该模型基于流体力与管束漩涡脱落相耦合的振动机理,改进了漩涡脱落对传热管振动的作用关系,并基于上述模型开发了蒸汽发生器流致振动评价软件。多个国际国内的通用设计规范如TEMA规范[3]、GB/T 151—2014《热交换器》[6]和《ASME Boiled and Pressure Vessel Code,Section 3,Division 1-Appendices》[7]等,均提出了换热器传热管流致振动的分析方法和评定依据。

盘管式冷却器由多层的盘管缠绕而成,由于每层盘管的几何结构和周围的流场分布较为相近,因此,选择其中一个盘管进行流弹失稳、湍流抖振和漩涡脱落的分析。由于流弹失稳、湍流抖振和漩涡脱落均需要传热管的流场信息作为输入条件,因此笔者首先采用计算流体力学方法对高压冷却器盘管进行流场分析,获得了盘管周围的流速分布,随后采用有限元软件,针对盘管的固有频率和模态振型进行分析,并采用TEMA[3]标准中针对传热管流致振动的判定准则对该盘管式高压冷却器的盘管进行流致振动的评定分析。

1 盘管的流场分析

所研究盘管式核主泵高压冷却器结构如图1所示。盘管的流场分析模型如图2所示。管内为二次侧,管外为高温高压的冷却剂,盘管材料为Inconel 690,其外径为38 mm,壁厚为4 mm。管外的流体平均流速约为0.1 m/s。盘管的螺距为50 mm;螺旋直径为500 mm,螺旋高度为1 200 mm。由于盘管式换热器由多圈盘管组成,各圈盘管依靠支承条固定,盘管之间的空间为冷却剂的流动通道,由于各圈盘管之间的结构相对独立,单个盘管结构紧凑,因此盘管之间形成的冷却剂通道相对独立,没有强烈的横向流作用。在进行盘管的流场分析时,笔者选取一个盘管沿轴向的通道模型进行分析,从而获得该盘管周围的流速分布,作为该盘管冷却器流致振动评定的流速输入。

图1 盘管式冷却器结构

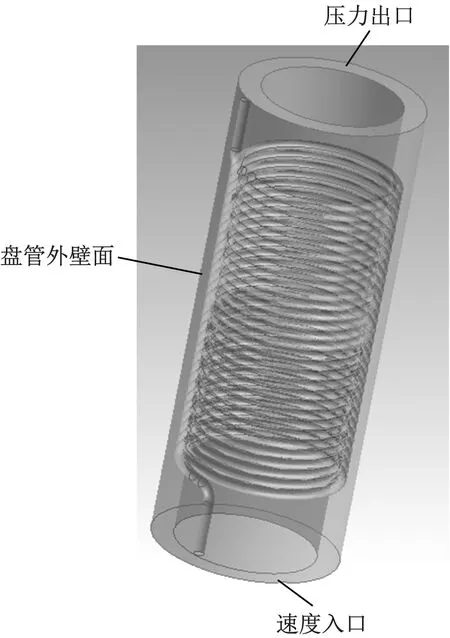
图2 盘管流场分析几何模型

计算采用商业计算流体力学分析软件STAR CCM+ 15.06。网格划分采用多面体网格,由于盘管间隙的空间较小,流速较大,为了更准确地反映冷却剂在该区域的流动特性,进而获得更准确的管间流速,因此需要对盘管间的网格进行加密,加密原则是确保管间距离最小处的网格数量大于10层。

不同的网格数量对计算的速度场有一定影响,因此需要进行网格无关性验证。选取网格数量分别为215万、257万、356万和483万,图3给出了不同网格数量下最大速度和压降的计算结果。从图3可以看出,当网格数量为356万和483万时,计算域最大速度和压降变化趋于平稳,考虑到计算效率,最终选择网格数量为356万,最终获得的横截面网格模型如图4所示。

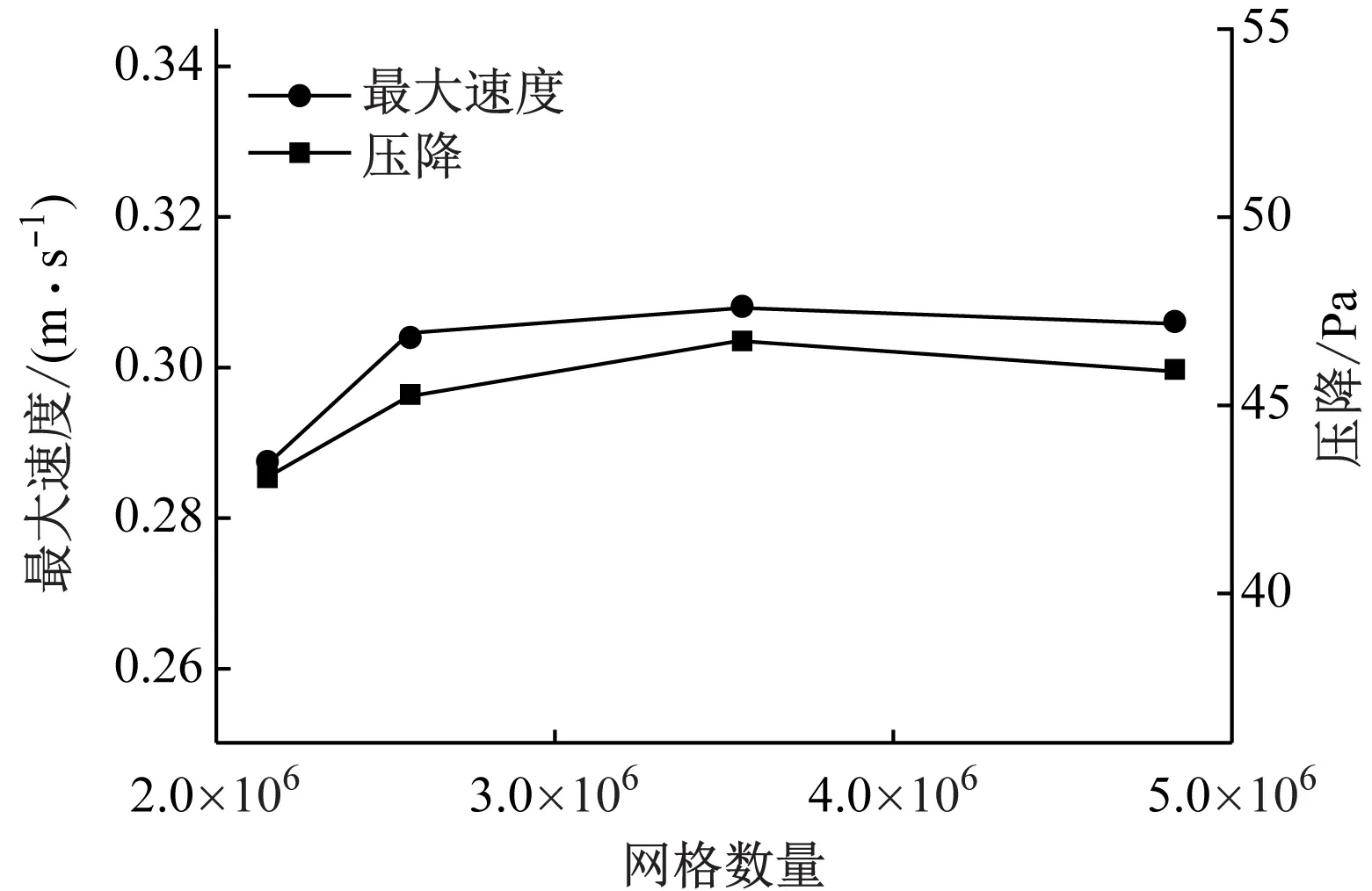
图3 网格敏感性分析结果

根据已知工况,计算得到雷诺数Re约为30 000,因此该流动属于湍流,选择工程计算中常用的“可实现k-ε模型”,壁面函数为“加强壁面函数”[8]。该计算为稳态不可压缩流动计算,采用速度入口和压力出口边界。求解算法采用SIMPLE算法,该算法全称为压力耦合方程组的半隐式方法,是一种压力修正法,通过“先猜想后修正的方法”获得压力场,并求解离散化的动量方程,该算法适用于稳态不可压缩流场的计算。

其中盘管入口冷却剂流速为0.1 m/s,出口的冷却剂压力设定为0 MPa。计算过程中监测进口压力和整个流体域的最大速度,当这2个参数变化幅度小于1%,认为计算收敛,并对结果进行后处理。

单个盘管的管外整体流场如图5所示。从图5可以看出,外流场速度最大处为流场横截面最小且靠近管壁处,最大横向流速度为0.25 m/s,选择该处流速作为盘管流致振动(包括流弹失稳、漩涡脱落和湍流抖振)评估的流速。

2 盘管的模态分析

盘管的材料为Inconel 690,其力学特性如下:密度为8.19×103kg/m3,弹性模量为8.19×103Pa,泊松比为0.289。

由于单根盘管的直径较细,长度较长,因此其刚度较低。为了避免盘管发生振动,需要增加支承以提高盘管的固有频率,因此在盘管上对称布置2根支承条。计算的边界条件为盘管两端固支,和支承条接触的区域为简支。

采用Ansys Workbench中的modal模块开展模态分析,中间支承采用简支,上下两端采用固支边界条件,模态分析中采用Block Lanczos算法。盘管的前20阶固有频率如图6所示。从图6可以看出,其基阶频率为26.68 Hz,随着模态阶数的增加,其第20阶的固有频率增大至539.58 Hz。基阶固有频率下盘管的振型如图7所示。

图6 盘管固有频率随模态阶数的变化

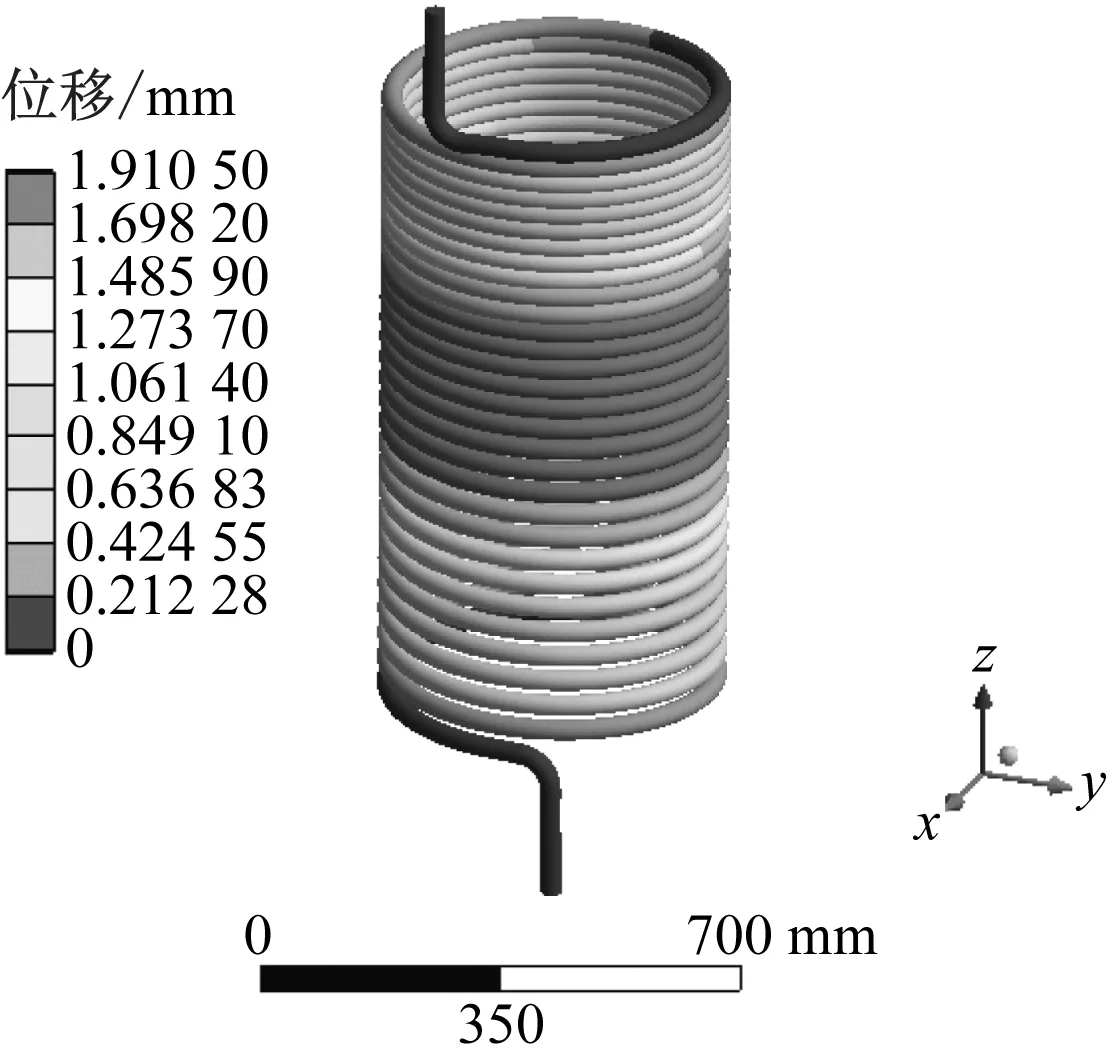
图7 盘管的基阶振型

3 盘管的流致振动分析

3.1 流弹失稳分析

流弹失稳是动态的流体力与盘管相互作用的结果。传热管产生的流体力不仅与管子本身的位移有关,也与邻近管的位移有关。针对流弹失稳机理,学者们提出了不同的数学模型,包括准静态流模型、准稳态流模型和非稳态流模型。准静态流模型假定作用在结构上的流体力与结构的位移成正比;准稳态流模型假定作用于结构上的流体力与结构的排列形式有关,并与速度成正比;非稳态流模型假定流体力是结构的位移、速度和加速度的函数。

针对工程计算而言,考虑模型的复杂程度和实用性,通常采用基于准静态流模型假设提出的Connors[9]临界流速半经验公式。利用该公式来判断特定结构的传热管发生流弹失稳的临界流速,进而评估其是否会发生流弹失稳,其表达式如下:

(1)

式中:Vc为临界流速,m/s;fn为传热管的n阶固有频率,Hz;d为盘管外径,m;C为Connors系数;ξ为临界阻尼比;ρ为管外流体密度;mt为盘管单位长度的总质量,kg/m,包括盘管质量、管内流体质量和流体附加质量。

Connors系数可根据管子排列形式、节径比和质量阻尼参数等确定。Chen[10]和Pettigrew等[11]针对直管传热管进行了上述参数的流弹失稳试验,获得了大量不同工况下的临界流速数据。笔者在流致振动评定过程中,统一采用TEMA标准[3],并认为管束之间为正三角形排列,针对Connors系数的计算式如下:

(2)

式中:P为管间距,m;D为盘管外径,m。

除了Connors系数,式(1)中临界阻尼比ξ的选择也至关重要。ξ表示管子本身阻尼对流体给予能量的耗散能力,该阻尼包括流体黏性阻尼、摩擦阻尼和压膜阻尼。Pettigrew等[12]给出了直管管束中3种阻尼的机理,并分别提出了相应的算法。但上述公式均是基于直管管束的试验结果拟合获得,而本文的盘管则是螺旋型结构,两者支承形式和在流体中的振动特点均有明显不同。

TEMA标准中的临界阻尼比较为保守[13],同时现有的标准中没有单独针对螺旋管流弹失稳的评定准则和临界阻尼比计算方法,因此本文计算中临界阻尼比按照TEMA标准[3]选取,其计算式如下:

(3)

式中:ν为管外流体黏度,Pa·s。

根据TEMA规定,当有效流速与流弹失稳临界流速的比值小于1时,认为不会发生流弹失稳。在设计上,为了确保设备安全,保守要求流弹失稳比设计值小于0.75。

经计算,盘管在各阶模态下的流弹失稳比为0.16,远远小于设计要求的0.75,因此该高压冷却器盘管不存在流弹失稳的风险。