阻尼器测试试验台的新变步长LMS 自适应滤波器设计*

丁兆轩 ， 刘凯磊，2，3 ， 强红宾，3 ， 康绍鹏

（1.江苏理工学院机械工程学院，江苏 常州 213001；2.国机重工集团常林有限公司，江苏 常州 213136；3.江苏大学流体机械工程技术研究中心，江苏 镇江 212013）

0 引言

近年来，随着我国经济和科技的发展，阻尼器的应用前景也越来越广阔。阻尼器测试试验台通过正弦波或三角波对被测阻尼器进行各种不同频率振动加载，模拟阻尼器在实际使用过程中所受冲击力大小和振动形式，进而得出阻尼器参数曲线[1]。由于在试验过程中阻尼器试验台受到加载力大小或执行件振动频率变化的影响，同时受被测阻尼器的力学性能和环境的干扰[2]，所以试验过程中数据精确快速的滤波反馈及后处理成为阻尼器试验台设计重点之一。

自适应滤波器由于其系统的闭环结构，相比其他滤波器更适用于对不确定的随机信号进行滤波处理。LMS 自适应滤波器是由Windrow 和Hoff 最先提出的，其利用瞬态均方误差求得权向量的梯度，从而对权向量进行更新迭代[3-4]。传统的LMS 算法有一个明显的缺点，就是调整步长因子，越长的步长因子收敛的速度越快，越小的步长因子，算法的稳态精确度就越高，该缺点限制了LMS 算法在一些情况下的应用[5]。

为了改善LMS 自适应滤波器的性能，众多学者针对该算法进行了大量研究。赵轶骁等[6]提出一种改进的变步长LMS 算法，即在算法中加入步长反馈因子，并对权值进行更新，使算法的收敛速度变快的同时保证了系统的稳定性，并加强了系统的跟踪能力。魏文亮等[7]提出了一种基于分段变步长LMS 自适应滤波和希尔伯特差值的互相关时延估计优化算法，改善了由于收敛速度和稳态失调之间的矛盾，从而影响时延估计精度的问题。

以上方式通过建立误差与步长因子的非线性函数表达式求得局部最优解或通过添加时延估计算法，提高了LMS 自适应滤波器的滤波性能。但如果能使步长因子始终处于全局最优解，便可以从根本上实现LMS最优的收敛速度和滤波性能。

为破解上述对自适应滤波器应用的限制，并进一步提高其算法的性能，本文在现有变步长LMS 自适应滤波算法的基础上，通过Tent 混沌算法对麻雀搜索算法（SSA）进行优化，进而优化LMS 自适应滤波算法在试验台上的应用，并通过LabVIEW 将其实现到了试验台的测试数据滤波。

1 传统LMS自适应滤波算法原理

传统的LMS 自适应滤波器使用横向FIR 结构采用最小均方准则，通过计算误差信号的均方误差，分析其性能曲线，并对瞬态误差的梯度向量进行估计，进而调整滤波器的加权系数[8]。LMS 自适应滤波器系统的闭环结构如图1 所示，输入信号为x(n)，参数矩阵为G(z)，输出信号为y(n)，期望信号为d(n)，误差信号为e(n)。

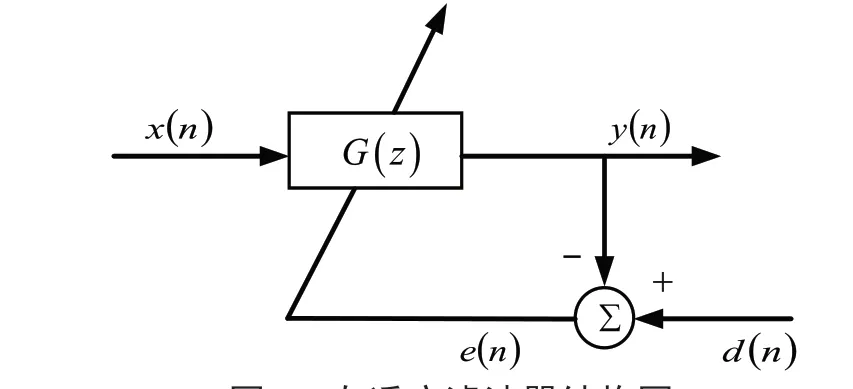
图1 自适应滤波器结构图

其算法流程可归结如下。

1）在n时刻输入信号x(n)与输出信号y(n)之间的滤波处理：

2）进行误差值的计算：

3）权系数矩阵的更新计算：

式中，μ为步长因子，其取值范围为0＜μ＜1/λmax，λmax为X(n)自相关矩阵的最大特征值。

2 麻雀搜索算法原理

麻雀搜索算法（Sparrow Search Algorithm, SSA）是Xue 等提出的一种新型群智能算法。其从对麻雀觅食行为和反哺行为的观察中受到启发，提出一种发现者-追随者模型，并为该算法加入侦查预警机制[9]。

该算法首先建立麻雀种群确认数量、迭代次数、发现者和追随者的比例，再通过迭代更新后，具有较好适应度的发现者位置更新表述如下：

式中，为t时刻雀群中第i只所在第k维的位置信息，t表示当前处于第t次的迭代，T为总迭代次数，R2∈[0,1]表示为预警值，ST∈[0.5,1]表示为安全值。Γ为服从正态分布的随机数L表示行为i列为k，元素均为1 的矩阵。当R2小于ST时，此时处于安全范围，可进行搜索。当R2大于或等于ST时，则此时预警值大于安全值，麻雀中的所有发现者向其他范围进行搜索。发现目标后追随者的位置更新如下式所示：

式中，为t+1 次迭代中雀群中第j只所在第k维的位置信息，为在t+1 次迭代中所处k维的最佳位，Xworst为当前所在k维的最差位，A为1 行多维的矩阵且各元素被随机赋值1或-1。当i大于时，则表示当前第i只适用度差的跟随者需要向其他范围搜索。警觉者的位置更新公式如下式所示：

式中，K∈[-1,1]为步长控制参数取值为随机数，fi为所处i麻雀的适应度值，fg与fw为全局最优位置和全局最差位置信息，ε为最小常数为当前的全局最佳位置。

3 基于改进SSA算法的LMS自适应滤波器设计

优化SSA 算法的初始种群对于其算法能力的提升具有一定的正面影响，当SSA 算法搜索接近全局最优解时，种群的多样性会无法避免地减少，这便使该算法陷入局部最优而非全局最优的问题，Tent 映射在其参数范围内系统处于混沌状态，而其产生的混沌序列具有全局遍历性，参数分布也较为均匀[10]。本文将Tent 混沌映射的方法引入SSA 算法中优化初始种群，从而提升算法性能，并将其运用到LMS 算法的步长计算中。

3.1 混沌映射算法

Logistic混沌映射为一种典型的混沌系统，被很多学者用于优化搜索问题[11]。而与Logistic 映射互为拓扑共轭映射的Tent 映射，相较于前者，更具遍历均匀性，其收敛性能更优越。Tent映射定义如下式所示：

式中，α为0.5 时，系统呈现短周期状态，在使用时应当避免，进而利用Tent 算法所得更具不确定性、不可预测、不可重复的优质种群代替SSA 初始种群进行优化。Tent 混沌映射与Logistic 混沌映射效果对比如图2 所示，Logistic 混沌映射在[0,0.1]和[0.9,1]两个范围值上的频次较高，种群较Tent 混沌映射更靠边缘而非均匀分布。

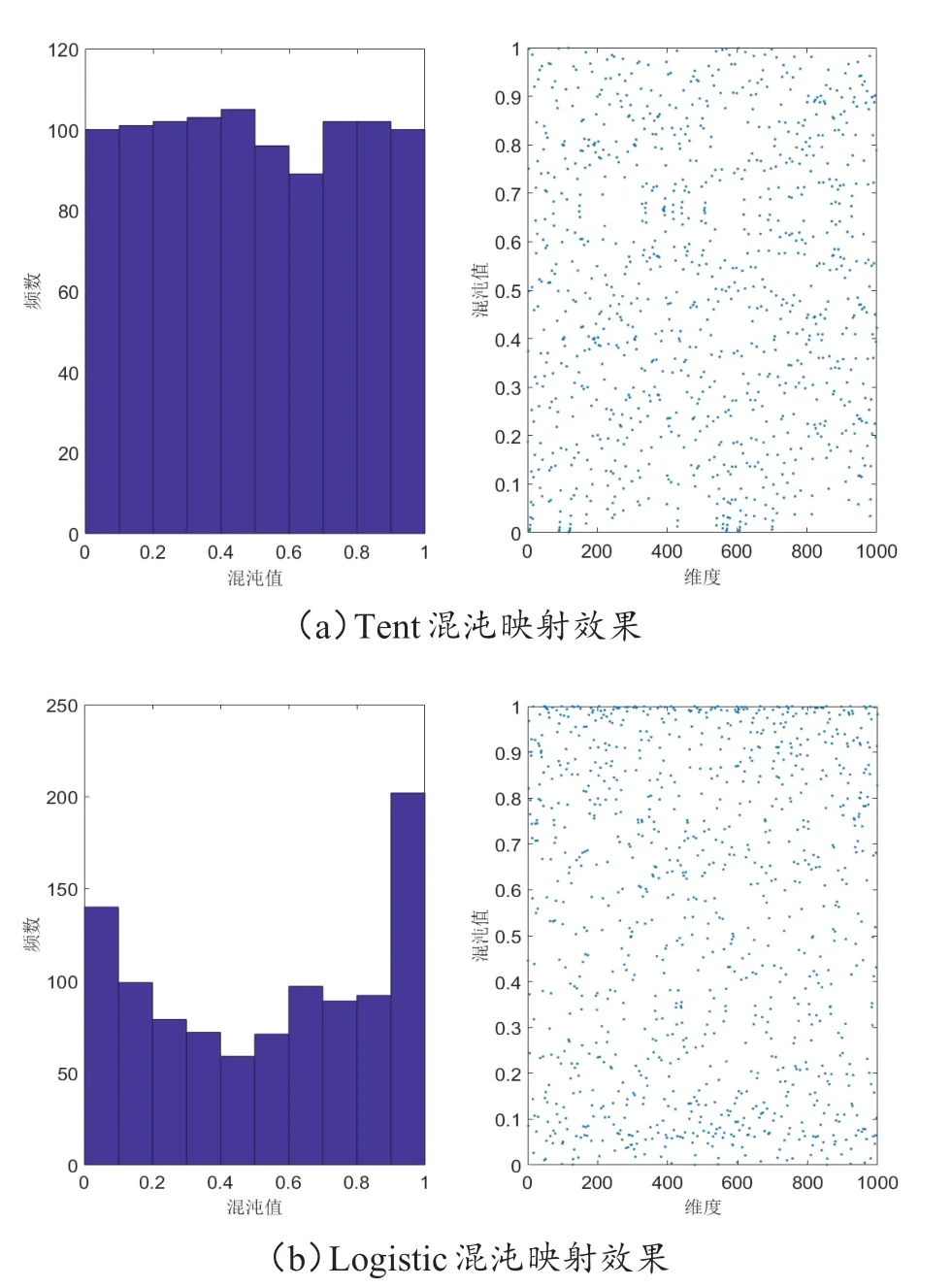
图2 混沌映射效果对比图

3.2 新的LMS自适应滤波器设计

基于改进SSA 算法的LMS 自适应滤波器对反馈数据滤波的模型具体建立过程如下：

1）对输入信号x(n)进行自适应滤波。

2）通过和期望信号d(n)比较进行误差值计算。

3）将步长因子μ作为目标参数，通过Tent 混沌映射生成初始种群，并设置边界参数以及发现者、追随者和警觉者的比重。

4）通过建立适应度函数计算麻雀的适应值。

5）更新发现者位置。

6）更新追随者位置。

7）更新警觉者位置。

8）判断是否满足算法结束的条件，若不满足，则前往步骤4，若满足则输出当前步长因子。

9）通过当前步长因子将最小均方差MSE 缩减至最小。

10）通过自适应滤波后输出信号y(n)。

4 算法仿真分析及应用实现

4.1 算法仿真分析

阻尼器试验台通过其执行机构输出不同频率、不同振幅的正弦信号，模拟阻尼器在实际使用时的工况，并以此检测阻尼器的特性参数。

本文利用MATLAB 软件进行算法仿真，在算法仿真的过程中，为更接近于试验台的实际使用要求，其仿真参数如下：输入正弦波幅值为5，振动频率为12 Hz，均值为0，方差为0.5 的标准正态噪声，采样点数为1 000，通过200次的独立仿真求其平均值。

SSA 算法优化前后在LMS 自适应滤波器中使用的效果对比图，如图3 所示，通过Tent 混沌映射优化前的误差总值约为10.42，优化后的误差总值约为2.53，下降约75.72%，优化效果较为明显。

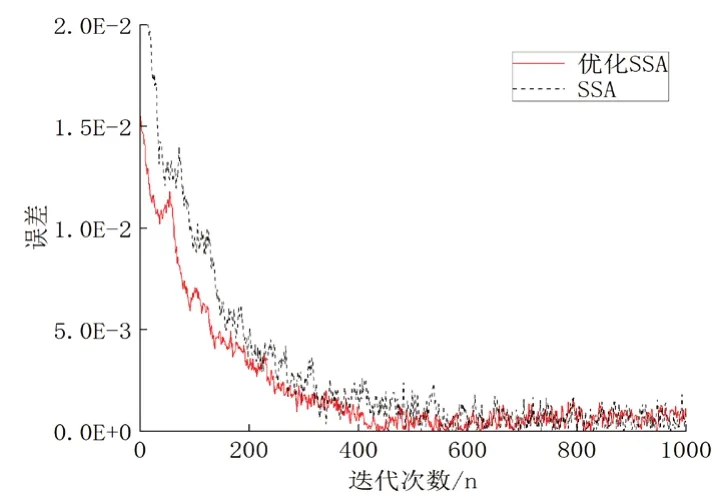
图3 SSA算法优化前后对比图

如图4 所示，优化后的LMS 自适应滤波器在具有高收敛速度的同时，保持较小的稳态误差，相较于其他文献算法，在抗干扰性和系统稳定性方面表现更好。文献[12]的算法误差和约为29.36，文献[13]的算法误差和约为28.09，本文算法误差和约为18.21，相较于文献[12]下降约37.98%，相较于文献[13]下降约35.17%。

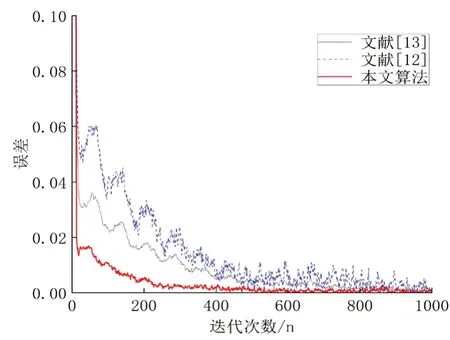
图4 本文算法与其他算法效果对比图

4.2 算法的应用实现

本文通过MATLAB 进行优化SSA 算法模型的建立，并使用LabVIEW 进行应用的实现，根据上述LMS 自适应滤波器模型进行应用的软件实现，其程序框图如图5所示。

图5 新滤波器程序框图

输入正弦波幅值为5，振动频率为10 Hz，均值为0，方差为0.5 的高斯白噪声的测试信号，测试其滤波效果。滤波前后的效果对比如图6 所示，在150 次的迭代滤波过程中其滤波效果较为良好。

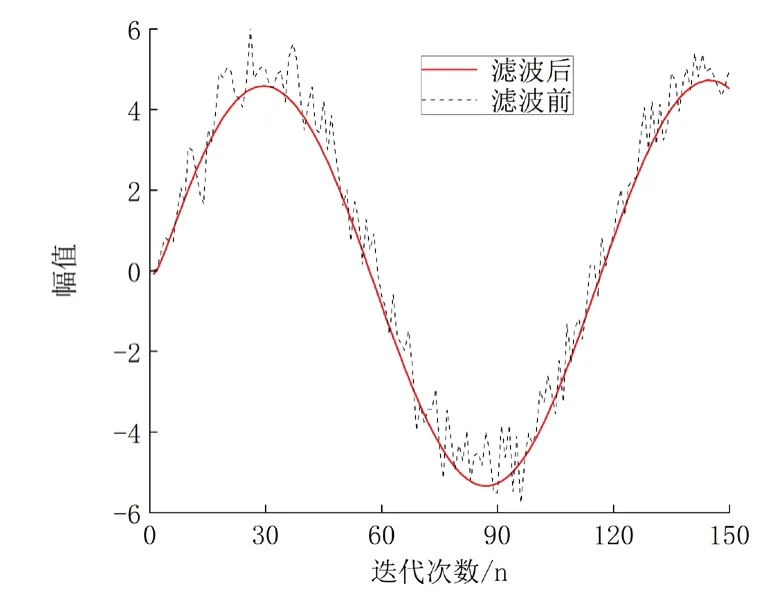
图6 滤波前后对比图

5 结论

1）通过Tent 混沌映射优化了SSA 算法在LMS 自适应滤波器中的应用，并通过仿真对比，优化后的算法较优化前误差总值下降约75.72%，其优化效果较为显著。同时，相较于其他文献中的LMS 自适应滤波算法，本文算法能在快速收敛的同时保持较低的稳态误差，误差总值下降约35.17%。

2）通过LabVIEW 实现该算法在软件中的应用。通过测试信号测试，该滤波器表现良好，具有较强的跟踪能力和稳态精度在低范围的保持能力，为阻尼器测试试验台性能优化和反馈数据的滤波提取提供了新的思路和方案。