二龙山水库弧形闸门支臂稳定性分析与优化

涂从刚,杜蔚琼

(水利部水工金属结构质量检验测试中心,郑州 450044)

0 引 言

弧形闸门是水利水电工程中常见的金属结构之一,弧形闸门具有启门时启闭力小、泄水时过流流态好、操作方便、工作可靠等优点[1-4],常作为水电站或水库的泄洪和排沙工作闸门。工程实际运行工况受到各种条件的制约和影响,运行过程中难免出现各种问题,闸门出现故障甚至失稳破坏的现象也时有发生,国内外已经出现多起弧形闸门失稳导致事故的案例。目前,国内外有多个学者对弧形闸门支臂稳定性问题做了较多研究,章继光等[1]运用屈曲挠角法基本理论,通过数值分析探讨了弧形闸门支臂的空间屈曲荷载求解方法;曹青等[3]利用NASTRAN软件对弧形钢闸门支臂的空间屈曲荷载影响因素进行了理论探讨;张全利等[4]以ANSYS为基础,使用有限元构建了6种加固撑及连接撑布置形式的支臂并分别进行屈曲分析,提出了弧形闸门空间支臂的稳定受限于受压支臂杆的稳定性的观点;丁峰等[5]利用ANSYS软件,对支臂的夹角、主梁截面尺寸、加固撑截面尺寸、斜支杆截面尺寸等参数对支臂屈曲稳定性的影响进行了详细分析,提出了主梁腹板高度对屈曲稳定性影响较大的观点;郑圣义等[6]利用ANSYS软件,结合6种常见的支臂纵向连接系的布置形式,研究了支臂纵向连接系的布置形式对闸门的固有频率的影响;赵春龙等[7]根据结构稳定理论推导出了同时考虑柱端转动刚度和侧向支撑刚度单根柱轴心受压下端部约束常数的普遍适用数学模型,应用于不同侧向支撑刚度以及不同柱端约束工况;徐强等[8]借助ANSYS APDL语言,以国内在建的跨度最大的大型平开弧门为例,分析了在静荷载作用下,主支臂夹角对闸门结构的影响,确定了最优的支臂夹角。从研究成果上看,弧形闸门支臂稳定性分析的理论研究较为成熟,各种商用有限元分析软件均具备结构屈曲分析模块,并在屈曲分析算法上吸收或借鉴了各行业的研究成果,能够对各种结构的线性或非线性屈曲稳定性、承载能力进行分析,能较为准确地预估导致失稳的临界载荷[9],但是对工程实际中出现的弧形闸门支臂失稳破坏原因进行分析的研究较少。因此,有必要在支臂稳定性理论研究的基础上,结合实际工程探讨支臂失稳原因,并提出相应的优化建议。

1 工程概况

二龙山水库位于陕西省商洛市区西北郊,距市中心4 km,是一座集防洪保安、生态供水、农田灌溉、水力发电、生态养殖为一体的综合利用年调节中型水库枢纽工程。水库始建于1970年,竣工于1973年,1974年正式蓄水投入使用;2002年进行除险加固。水库总库容8 100万m3,正常库容5 700万m3。水库枢纽工程由浆砌石重力大坝、泄水孔、发电引水隧洞、坝后式电站、灌溉引水涵管等部分组成,大坝按50 a一遇洪水设计,500 a一遇洪水校核。

水库左岸泄水孔弧形闸门为单节弧形门叶,双支臂,门叶顶部设置单吊耳,闸门配套启闭机为320 kN液压启闭机,闸门工作方式为动水启闭。闸门孔口尺寸为2.0 m×2.4 m(宽×高),闸门曲率半径4.8 m,支臂中心距0.9 m,门叶厚度0.552 m,设计水头41.33 m,校核水头46.34 m,面板总水压力2 810.8 kN。闸门门叶、支臂等主要结构材料为Q235B钢。

本文以水库左岸泄水孔弧形闸门为研究对象,该闸门在汛期泄洪启门过程中突然出现支臂失稳导致闸门破坏,后期专项检测结果表明该闸门支铰的安装误差超标,经过专家研判分析,支铰同轴度的安装误差尚不足以导致支臂破坏,结合现场支臂破坏的情况推断支臂强度和稳定性可能是导致该次事故的主要因素。支臂破坏情况如图1所示。

图1 弧形闸门支臂破坏情况Fig.1 Damage condition of radial gate arm

因闸门支臂破坏出现在泄洪启门过程中,根据动水启门工况建立闸门的载荷与约束边界条件,建立弧形闸门有限元模型,并进行静强度计算,再以静强度计算结果为基础进行弧形闸门整体结构线性屈曲分析并提取前6阶屈曲特征值,从强度和稳定性两个方面来分析支臂破坏原因。

2 弧形闸门有限元建模

2.1 有限元模型建立及材料参数

在SolidWorks中根据设计图纸完成弧形闸门门叶、支臂及支铰等主承力构件的三维模型,建模过程中省略了止水橡皮、螺栓孔、支臂检修人梯等非承力构件。以STEP格式导入ANSYS Workbench,使用相应的单元进行网格划分。面板、主横梁、纵梁、吊耳及支臂等规则结构板件使用八节点六面体实体单元Solid185,支铰等不规则构件使用Solid185单元退化后的四节点四面体形式,根据模型尺寸将单元网格尺寸设定为20 mm,采用多点约束(Multipoint Constraint,MPC)方式实现装配体各部件的单元节点的连结,完成有限元模型。弧形闸门的门体与支臂的主要材料为Q235B钢,按照《水电工程钢闸门设计规范》(NB 35055—2015)[10]的要求,材料参数取值:弹性模量E=2.06×105MPa,泊松比μ=0.30,密度取7 850 kg/m3。

2.2 工况选择及边界条件设定

闸门支臂破坏出现在泄洪过程启门操作,因此本文主要考虑弧形闸门的动水启门工况,并参考闸门的挡水工况作为对比。弧形闸门挡水工况的荷载组合方式为动水载荷+闸门自重,载荷边界条件设置如下:面板上设置静水压力,静水压力按照设计水头41.33 m设定,并按规范要求,静水压力乘以动载系数1.2[10]以模拟动水载荷,闸门底缘中点处设置系统坐标系CSYS(Coordinate of System)使水压参考高度以门叶底缘为起点,x轴指向主横梁轴向,y轴指向重力反方向,z轴指向水流下游方向;环境重力加速度g=9.8 m/s2。约束边界条件设置如下:支铰座固定约束,支铰轴同铰链轴孔内设置销钉约束,释放支铰的旋转自由度,两侧边梁止水橡皮安装面设置无摩擦约束;吊耳孔内设置竖向位移约束启门方向,以模拟启闭机对闸门的闭锁作用。动水启门工况的荷载组合方式为动水压力+闸门自重+启闭力,动水压力载荷参照挡水工况的水压载荷,约束边界条件设置如下:支铰座固定约束,支铰轴同铰链轴孔内设置销钉约束,两侧边梁腹板止水橡皮安装面设置摩擦约束,吊耳孔内y方向设置启门力320 kN,门体底缘设置无摩擦约束, 环境重力加速度g=9.8 m/s2。弧形闸门动水启门工况以及挡水工况载荷及约束边界条件见表1。

表1 弧形闸门动水启门工况以及挡水工况载荷及约束边界条件Table 1 Load and constraint boundary conditions of radial gate under dynamic water discharge and dynamic water retaining condition

弧形闸门门叶及支臂结构的材料为Q235B钢,适用于VonMises屈服准则第四强度理论进行安全评价,闸门设计规范规定了材料的许用应力要根据闸门重要程度和工作工况强度取不同的应力折减系数[10],《水工钢闸门和启闭机安全检测技术规程》(SL101—2014)[11]规定结构件许用应力需按照闸门工作年限取时间折减系数,经折减处理后的许用应力如表2所示。若闸门在设定载荷下,构件大部分区域的等效VonMises应力小于表2中Q235B钢折减后抗拉、抗压和抗弯许用应力,那么构件的强度合格,可看作是安全的[12-13]。

表2 Q235B钢闸门折减调整后许用应力Table 2 Allowable stress of Q235B steel gate after adjustment

3 弧形闸门支臂强度分析

有限元模型求解完成后,在ANSYS Workbench后处理中提取挡水工况下弧形闸门结构整体及支臂构件的等效VonMises应力及空间分布情况,见图2。

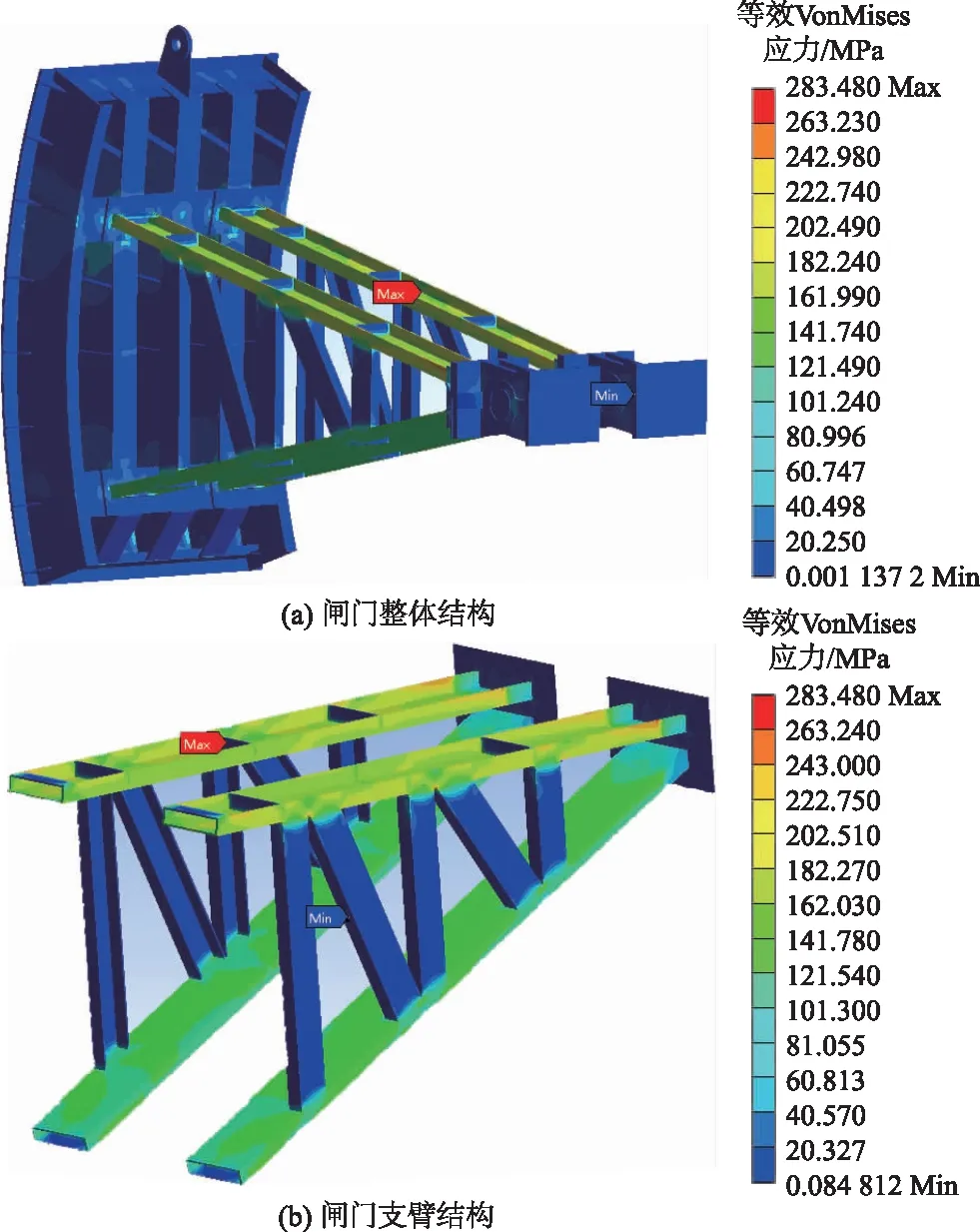
图2 挡水工况闸门整体结构、支臂结构等效VonMises应力分布Fig.2 Equivalent VonMises stress distribution of radial gate structure and radial gate arm structure under dynamic water retaining condition

结果表明:在挡水工况下,弧形闸门门叶的面板、主横梁、纵梁、边梁等主承力构件大部分区域的等效VonMises应力小于结构材料的抗拉、抗压和抗弯许用应力,门叶结构强度满足要求;但是支臂结构的整体等效VonMises应力高于闸门门叶,而且上支臂的等效VonMises应力明显偏高且高于下支臂。上、下支臂腹板沿臂柱长度方向等效VonMises应力曲线如图3所示(应力路径为腹板构件同外翼缘交界处边缘)。数据显示,挡水工况下,上支臂腹板的等效VonMises应力分布范围为184～199 MPa,超过了闸门材料的抗拉、抗压和抗弯许用应力,而在靠近支臂与支铰连接处的弯曲失效位置附近,腹板的局部等效VonMises应力计算值在249 MPa左右;下支臂的等效VonMises应力大部分为110～160 MPa,靠近门叶连接部位的局部等效VonMises应力达到155 MPa,也超过了材料的抗拉、抗压和抗弯许用应力;属于应力集中区域。

图3 不同工况上、下支臂沿长度方向等效VonMises应力曲线Fig.3 Curves of equivalent VonMises stress of upper and lower arms along length direction under different working conditions

按照闸门设计工况,该闸门需要在动水中启闭,启门工况是上支臂受力较大的工况。如图3(b)所示,弧形闸门启门时,上支臂腹板和翼板各处的等效VonMises应力相比挡水工况下增大了20 MPa左右,上支臂在靠近门叶连接处出现最大峰值等效VonMises应力249 MPa,超过了材料的屈服强度,整个上支臂腹板的等效VonMises应力分布范围为210～230 MPa,在靠近支铰处,上支臂的等效VonMises应力降低,下支臂的等效VonMises应力急剧升高至最大峰值214 MPa,超过了材料抗拉、抗压和抗弯许用应力。

综上所述,弧形闸门在挡水工况和启门工况下,支臂结构的强度不符合规范要求,反映在实际状况中,弧形闸门在动水中启门操作时,在动水载荷和启门力共同作用下,上支臂始终处于高应力状态,部分区域的应力超过了钢材的屈服极限,支臂强度不足是造成支臂结构失稳破坏的一个显著因素。

4 弧形闸门支臂稳定性分析

支臂结构是弧形闸门的主要传力、受力构件,设计时除了应该满足强度要求,支臂框架还应在外力作用下保持稳定性,支臂结构的稳定是整个闸门结构稳定的基础。

闸门结构稳定性分析即特征值屈曲分析。特征值屈曲分析是用于确定结构开始变得不稳定时的临界载荷和屈曲模态形状的技术[5],用于预测一个理想结构的理论屈曲强度,即通过特征值的公式计算造成结构负刚度的应力刚度矩阵的比例因子,其通用数学模型为[1,3,6,9]:

([K]+λ[S]){Ψ}=0 ;

(1)

Pcr=λP。

(2)

式中:[K]为刚度矩阵;[S]为应力刚度矩阵;{Ψ}为位移特征矢量;λ为特征值,也称之为载荷因子;P为给定载荷;Pcr为临界载荷。通过式(1)能够计算出结构在给定载荷下的特征值,即在给定载荷P的λ倍临界载荷Pcr下结构出现失稳[3,6]。ANSYS Workbench中的特征值屈曲分析模块能够计算结构不同模态的特征值以及对应的屈曲模态,通过模态的变形趋势判断出结构的薄弱部位。特征值屈曲分析计算速度较快,能够初步预测临界载荷范围。

在ANSYS Workbench中静力结构分析结果的基础上进行线性特征值屈曲分析,以载荷边界条件为结构预载荷。本文采用计算效率较高、ANSYS中的默认算法[14-15]Block Lanezos(兰索斯分块法)求解屈曲特征值。求解完成后提取前6阶屈曲因子及屈曲模态,前6阶屈曲因子计算结果如表3所示。

表3 弧形闸门线性屈曲前6阶屈曲因子Table 3 The first six order buckling factors of the linear buckling of radial gate

根据数据处理结果分析,弧形闸门的1阶屈曲因子仅为1.58,屈曲模态如图4所示(图中的数据代表结构在出现屈曲失稳后,局部失稳部位的理论综合位移)。2阶屈曲因子仅为1.62。前2阶屈曲因子较小,表明弧形闸门的结构稳定性偏弱。

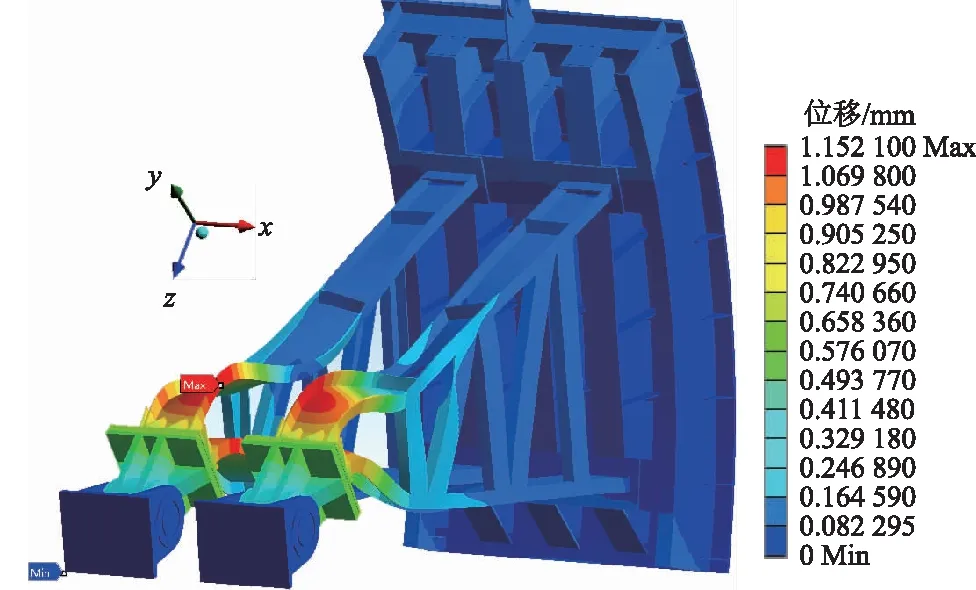
图4 弧形闸门线性屈曲1阶屈曲模态Fig.4 First order buckling mode of linear buckling of radial gate

通过前2阶屈曲因子的屈曲状态可看到,支臂在临界载荷下屈曲失稳时,在靠近支铰处的上、下支臂均出现绕横轴的弯曲,根部的加强板并未起到加强作用,因低阶屈曲通常发生于高阶模态之后,1阶屈曲模态和特征值更能反映结构的失稳特征[16-18]。1阶屈曲模态与工程现场闸门支臂失稳破坏状态完全一致,说明弧形闸门屈曲破坏的根本原因是支臂构件截面抗弯能力不足以及根部加强板作用较弱。因此建议改造时应重点加强支臂构件截面的抗弯强度以及加强板的设置。

5 支臂改造建议

弧形闸门的上、下支臂是受力较大的构件,对闸门动力作用产生的轴力非常敏感,其截面特性与支臂的稳定性有很大关系[19-21]。为保证该弧形闸门同孔口尺寸匹配,弧形闸门支臂结构空间尺寸(左右支臂中心距、支铰中心至门叶主梁后翼板距离等)保持原设计不变,将支臂原槽钢梁结构重新设计为箱型梁结构,原槽钢宽度320 mm,高度88 mm,箱型梁腹板宽度仍为320 mm,两侧翼板高度由88 mm调整为140 mm,上下腹板内侧间距68 mm,腹板和翼板厚度加大至16 mm。考虑原支臂屈曲特征为靠近支铰处根部折弯,再在支臂裤衩部位布置大尺寸加强板以增加支臂根部的强度。弧形闸门原方案设计及支臂截面尺寸见图5,箱型梁支臂方案设计及支臂截面尺寸见图6。

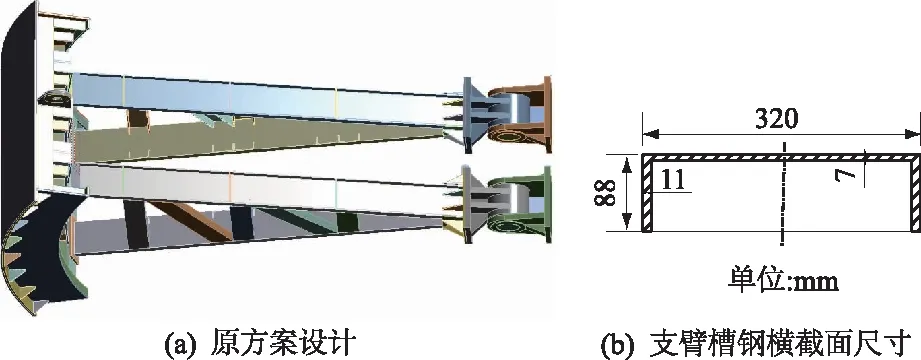
图5 弧形闸门原方案设计以及支臂槽钢横截面尺寸Fig.5 Original design scheme of radial gate and cross-sectional dimensions of arm

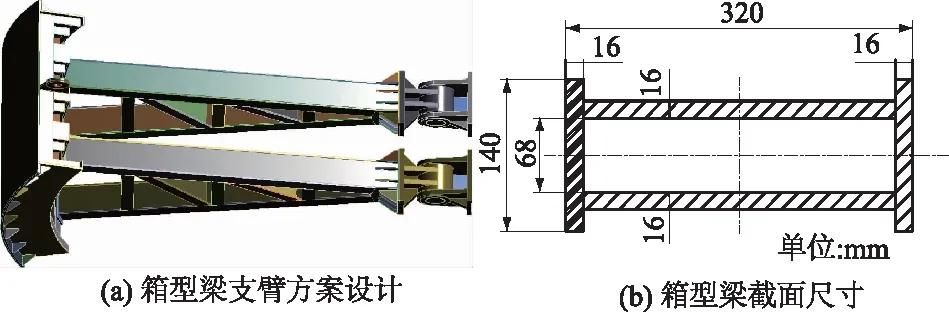
图6 弧形闸门箱型梁支臂结构方案设计以及箱型梁截面尺寸Fig.6 Design scheme of radial gate with box beam arm structure and the cross-sectional dimensions of box beam

为了验证支臂改造的可行性,对新支臂结构的弧形闸门再次进行强度计算和线性特征值屈曲分析,载荷和约束边界条件不变。强度计算结果表明,箱型梁结构支臂的截面抗弯能力得到增强,支臂裤衩部位的加强板增强了支臂结构的稳定性,新支臂的等效VonMises应力大幅度减小,等效VonMises应力分布如图7所示;最大等效VonMises应力由原来的249 MPa降低到63 MPa左右,支臂杆件长度方向应力变化幅度平稳,如图8所示。

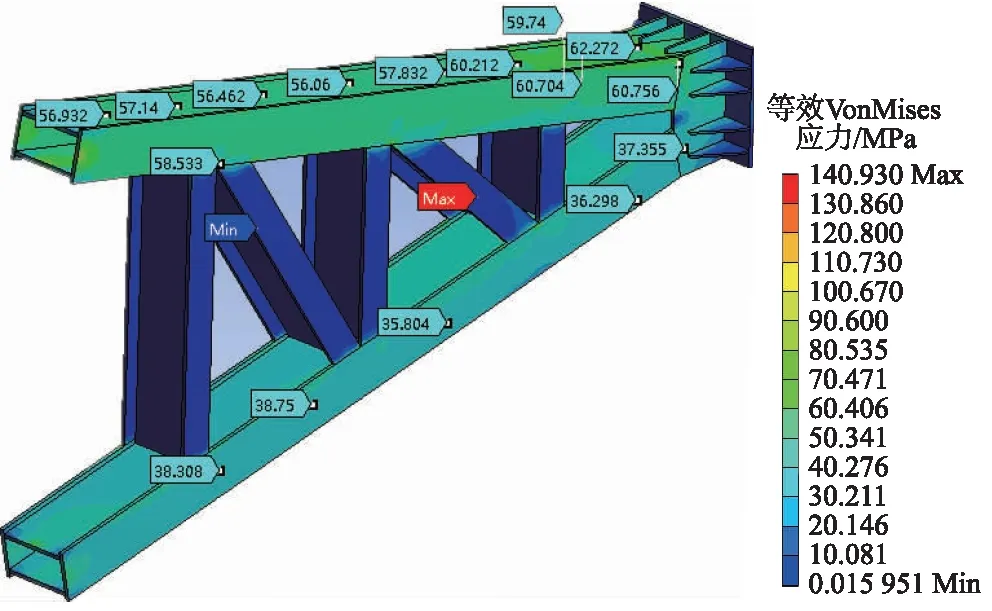
图7 动水工况下弧形闸门新方案支臂沿长度方向等效VonMises应力分布Fig.7 Equivalent VonMises stress distribution along the length direction of new arm under dynamic water condition

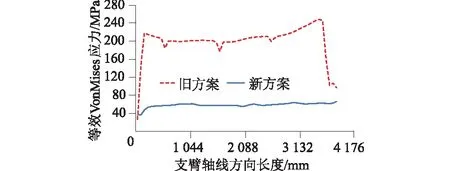
图8 动水工况下弧形闸门新旧设计方案上支臂等效VonMises应力分布曲线Fig.8 Equivalent VonMises stress distribution curves of upper arm in both new and old schemes under dynamic water condition

线性屈曲分析结果显示,箱型梁支臂结构的1阶和2阶屈曲因子均增大至10.93,一阶屈曲模态如图9所示。2种屈曲形态均表现为箱型梁腹板的局部微小变形,不影响整个结构的稳定性。前6阶屈曲因子如表4所示。

表4 新支臂方案的弧形闸门线性屈曲前6阶屈曲因子Table 4 The first six order buckling factors of linear buckling of radial gate in the new arm scheme

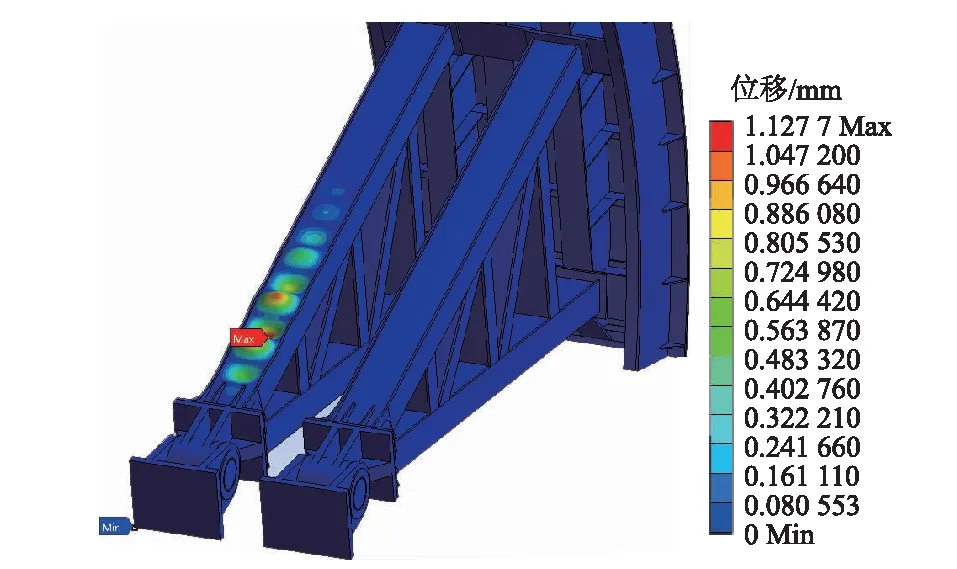
图9 新支臂方案线性屈曲1阶屈曲模态Fig.9 First order buckling mode of linear buckling of new arm scheme

综合分析可知,弧形闸门采用箱型梁支臂结构并对支臂裤衩加强板进行调整,结构强度和稳定性得到大幅增强,其可行性得到验证。

6 结束语

通过前期二龙山泄水孔弧形闸门专项检测结果和对现场支臂破坏情况的勘查分析研判,初步推断闸门支臂失稳破坏与支臂的强度和稳定性有密切关系。建立有限元模型进行支臂强度分析,结果表明,弧形闸门在挡水工况和启门工况下,支臂结构的强度不满足规范要求,在动水中启门时,上支臂始终处于高应力状态,部分区域的应力甚至超过了钢材的屈服极限;支臂稳定性分析结果表明支臂构件的截面抗弯能力不足,屈曲模态与支臂失稳破换的状态完全一致。印证了支臂失稳破坏的推断。同时根据水库除险加固的要求,设计箱型梁结构型式的支臂并进行验算,支臂强度和稳定性得到显著提高,满足安全要求。该方法对其他水利工程类似弧形闸门的安全评价与改造有一定的参考价值。但是闸门结构形式的改变还应考虑配套启闭机容量的复核,确保满足启闭机容量要求,这是本文的不足,还有待下一步研究。